基于车流波动理论和排队论对昆明小西门交通的优化研究

◎刘平清　张鹏　徐刚刚

基于车流波动理论和排队论对昆明小西门交通的优化研究

◎刘平清张鹏徐刚刚

本文利用车流波动理论求出车辆排队长度，并利用排队论计算平均有效延误时间，再基于平均有效延误时间最小对小西门交通灯周期及相位时间进行优化设计。

城市交通问题越来越受人们关注，我国每天因城市交通拥堵而造成数十亿的损失，同时由此而导致对生态环境的影响更是惊人。就目前而言，关于交通灯的配时方法，国际上主要有英国的WEBSTER算法，而我国有停车线法和冲突点法等。周玉等在一类休假排队模型研究了一个十字路口的红绿灯问题，得出了在一个普通的十字路口分派红路灯的最佳时间。熊桂等利用排队理论对交通阻抗问题进行了研究和分析，并给出了具体的函数表达式。

对小西门模型的分析

本文基于小西门的具体情况，先对其目前情况进行分析，然后提出优化方案，并对优化方案进行数值计算。

对小西门当前设计的分析。通过对实地交通流量数据的收集和整理，并结合文献中对相关量的推导计算可得表1如下：

表1：各进道口流量、大车率以及优化前流量比

这里用文献中webster算法来判断其目前的设计是否合理，可计算路口通过效率为：

y=0.3391917+0.1951892+ 0.1843491+0.2420087=0.96073

由于y＞0.9，因此该原设计是不合理的，应该重新设计。

设计优化方案。根据实际情况，改进设计可分为对进道口设置的改进、对相位设计的改进或者对二者同时进行改进。小西门的红绿灯目前采用的是：相位周期为160（s），进道口有一条右直合并道，一条左直合并道，4个相位，并且对同一路口的直行、左转同时放行。通过对实地数据的收集发现，该路口左转、直行、右转的车流量都比较大，而我国右转车只要保证安全是可以不受红绿灯控制的，经过计算，在小西门处进行右直车道合并会降低路口通过效率，不能满足设计要求，则将右直合并车道分开；而左直车道合并情况下相位只能采用各个路口分别放行；又由流量数据分析两相位和八相位都不能起到优化作用，因此仍采用4相位。进而优化分为如下两种情况：

（1）存在左直合并车道

则进道口设计考虑的情况就得以简化为如下：

图1　：(1)型优化后的车道简易图

此时路口只能是对单个方向分别放行，放行顺序并不影响交通情况，不妨照图1中路口编号①→②→③→④的顺序放行。

通过类似（1）式的算法，可以得到改进后的不同流量比之和为：

Y=0.8773316＜0.9

（2）不存在左直合并车道

则进道口设计考虑的情况就得以简化为如下：

图2　：（2）型优化后的车道简易图

（注：由于对实际流量数据的收集发现，直行流量＞左转流量，故直行设两条道）此时就分为同时对相位进行改进设计或者相位保持不变两种，又由于该交叉口存在左转，因此要求各个相位的绿灯时间不会出现错车情况（合流作为错车一种），则对相位的设计也可分为以下两种可能情况：

i：同一路口左转与直行同步：照图2中路口编号①→②→③→④的顺序放行。

ii：同一路口左转与直行不同步：照图2中路口编号，第一相位放①③直行，第二相位放②④左转，第三相位放②④直行，最后第四相位放①③左转。

同理可求得改进后的不同流量比之和：i：同一路口左转与直行同步时路口通过效率：Y1=0.8728783＜0.9

ii：同一路口左转与直行不同步时路口通过效率：Y2=0.8609154＜0.9

由计算可知：通过对进道口的两种改进道路设计以及相位的变化可以有效的改善道路通行状况。下面将对两种进道口设计进行具体的数值计算。

对优化方案的计算。首先，由车流波动理论可以计算出在等待时间的队长Q：Q=

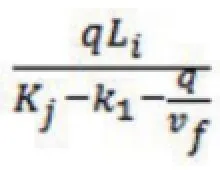
其中Li、q、k1、Vf分别为该进道口绿灯等待时间、进道口车流驶入流量、进道口车流驶入密度、进道口车流未受影响前的驶入速度（各路口都相等Vf=8m/s），Kj为饱和密度。各个路口数据采用实地观测数据，并可以求得：离开路口时车流波的速度：V1直=4.1667m/sV1左= 3.7037m/s

以S表示一条进道口的饱和流量，然后根据排队论知识：

波传至最远处所需时间受限车数平均延误时间总延误时间

根据上表公式可以计算四个路口在（1）型进道口设计下总延误时间D和处理会车总时间F，以及在（2）型进道口设计下i、ii两种相位下的总延误时间D1、D2和处理会车总时间F1、F2分别为：

进而可以求出（1）型进道口设计下的平均有效延误时间V，以及（2）型进道口设计下i、ii两种相位的平均有效延误时间V1、V2分别为：

由实际情况可知：

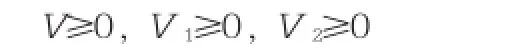
由于对具体一辆车而言，其处理会车的时间是一定的，那么当进道口设计和相位设计确定后，其等待时间（Li）越长则对应的平均有效延误时间越大。由此可知：（1）、（2）型进道口设计当相位变化周期C0在（11）、（12）式条件下取得的最小值（即最短周期）即为（1）、（2）型各自的最优周期。

又由交通信号灯相位设计易知：

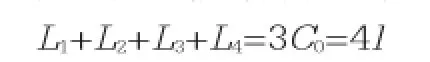
其中：l为绿灯间隔时间（黄灯时间），我国通常l=3s；Li为第i个路口等待时间。

并且通过分析我们知道，需要保证一个周期之内，红灯能通过的车辆数必须不小于同周期等待时间到来的车辆数，否则该路口的就是不稳定的，排队车辆长度会趋于正无穷。以X表示该进道口某种通行形式（直行、左转）的进道口条数，S表示该种行形式（直行、左转）的饱和流量，因此还需要有如下约束条件：

XS(1 HV)(C Li)≥qLi

则问题转化为（1）、（2）型进道口设计在（12）、（13）、（14）式的约束条件下求（11）式的极小值；并通过R3.2.1版本编程可以求得（1）型进道口设计下的最短周期C和（2）型进道口设计下i、ii相位的最短周期C、C分别为：

可求出（1）、（2）型进道口设计下每辆车平均有效延误时间V、V1、V2分别为：

由V1＜V2＜V可知：（2）型进道口相对优于（1）型相位，且（2）型进道口设计下的i型相位略优于ii型相位。

进而可计算得(2)型进道口设计下i型相位优化后各相位等待时间Li和绿灯时间Gei为：

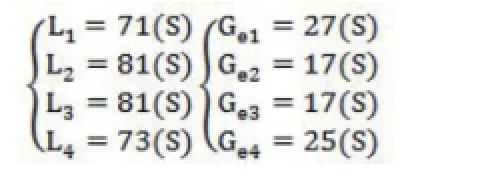
经过分析，对小西门的交叉口设计采用模型（2）进道口设计中的i型相位，即进道口道路不合并，右转不受红绿灯限制，采用同一路口直行与左转同步的放行。且红绿灯周期为C=98（s），各个周期的时间分配见（17）式。

通过对（1）、（2）型进道口设计结果的比较，并进一步研究在不同周期下平均有效延误时间,可得到表2如下：

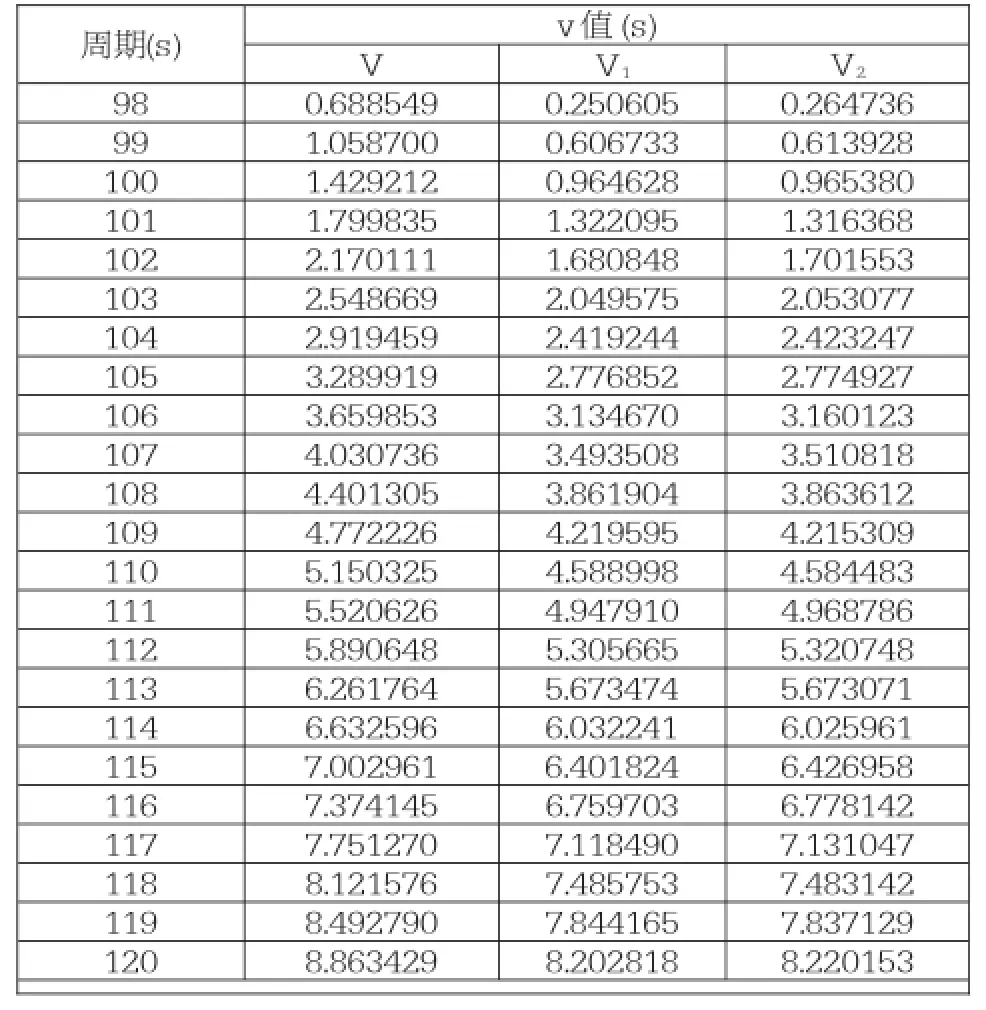
表2：在不同周期下各设计的平均有效延误时间

由表2可知：针对小西门处的实际情况，当交通灯相位数确定，影响设计的最大因素是相位周期，一旦最优周期确定，进道口设计和相位设计影响相对较小。

（作者单位：云南大学数学与统计学院）