基于网格的缩短(38，26)BCH码的自适应维特比译码算法

侯舒娟， 宋灵燕， 孙琳

(北京理工大学 信息与电子学院，北京 100081)



基于网格的缩短(38，26)BCH码的自适应维特比译码算法

侯舒娟， 宋灵燕， 孙琳

(北京理工大学 信息与电子学院，北京 100081)

针对伽利略搜救系统(Galileo/SAR)物理层协议中采用的缩短(38，26)BCH码，提出了一种自适应维特比译码算法(AVA). 文中给出了缩短(38，26)BCH码的最优网格，在此基础上，提出了AVA，该算法在维特比译码算法(VA)的基础上设计了一个丢弃门限，只保留最有可能的路径. 丢弃门限值随着信噪比的变化，可以自适应调整，使得AVA在保持与VA几乎相同的误码率性能的基础上，尽可能地降低译码复杂度. 同时，文中给出了丢弃门限的估计方法，并确定了不同信噪比下的最佳丢弃门限值. 仿真结果表明具有最佳丢弃门限的AVA在保持与VA误码性能几乎相同的基础上，译码复杂度有着极大程度的降低，特别是在信噪比高时，译码复杂度下降得更加明显.

AVA；丢弃门限；缩短BCH码；伽利略搜救系统

伽利略搜救系统(GALILEO/SAR)是全球卫星搜救系统(COSPAS-SARSAT)的一部分[1]，其信标信号采用的编码方式之一便是缩短(38，26)BCH码. 对于该缩短码，可采用经典的BM算法[2]对其进行译码，但是BM算法的运算量较大. 文献[3]对BM算法进行了改进，提出了一种新的迭代停止准则，减小了译码复杂度和译码延迟. 然而，经典BM算法和改进BM算法都是硬判决译码算法，误码率性能较差. 改进BM算法对应的软判决译码算法是Chase-2算法[4]，仿真结果表明，相比改进BM算法，Chase-2算法有0.5 dB的编码增益，但是，Chase-2算法仍然是一种次优的译码算法.

为了寻找缩短(38，26)BCH码的最优译码算法，本文研究了线性分组码的网格构造方法. Wolf在文献[5]中首先提出了线性分组码的网格构造方法，随后，Forney[6]和Lin[7]证明了一些线性分组码具有相当简单的网格结构. 文献[2，8-9]中研究了最小网格的构造、网格的并行分解方法、网格的一般化图形表示方法，以设计出效率更高的基于网格的译码算法，使得实现线性分组码的最大似然译码时，大大降低译码复杂度. 常用基于网格的译码算法是维特比译码算法(viterbi algorithm， VA)[10]，该算法遍历所有码字，实现了最大似然译码. 但是，其缺点在于译码复杂度与网格的状态数成正比，因此，实际中通常限制网格各时刻状态数不超过256，当网格状态数过大时，将不利于译码算法的实现.

另一方面，人们在研究卷积码的译码算法时，提出了自适应维特比译码算法(adaptive viterbi algorithm， AVA)[11]，该算法是VA的改进算法，在VA基础上增加了丢弃门限判决，减小了译码复杂度. 文献[12-14]中对卷积码的AVA算法进行了改进，进一步减小了译码复杂度，并且设计出了性能更好的AVA译码器结构.

本文基于线性分组码的网格构造方法和卷积码的AVA译码算法，针对缩短(38，26)BCH码，提出了一种软判决自适应维特比译码算法，该算法在保证与VA几乎相同的误码性能的基础上，极大地减小了译码复杂度. 同时，本文还探讨了丢弃门限的估计方法，仿真结果验证了该估计方法的有效性. 值得指出的是，尽管本文的初衷是针对缩短(38，26)BCH码，研究其最优译码算法，但是，本文所提出的方法并不限于缩短(38，26)BCH码，由于短码或者中等长度的线性分组码的网格复杂度适中，可以采用AVA算法，所以对于所有短码或者中等长度的线性分组码，本文所提出的方法都是适用的.

1 缩短(38，26)BCH码的最优网格构造

考虑GF(2)中的(n，k)线性分组码，其生成矩阵是G. 采用高斯消去法，将G变成面向网格的矩阵GTOGM[2].GTOGM有两个特点：

① 每一行的首1所处的列在其下方各行的首1所处列之前；

② 没有两行的尾1在同一列.

令g=[g0g1…gn-1]为GTOGM的一行，区间[i，j](0≤i≤j≤n-1)表示g中所有非零元素的最小指标区间，定义为g的比特跨度，gi和gj分别是g的首1和尾1. 定义g的时间跨度为[i，j+1]，有效时间跨度为

(1)

首先构造(n，k)线性分组码的比特级网格. 记C是(n，k)线性分组码的码字集合，假设已经完成了第i段网格的构造，现在构造时刻i到时刻i+1的第i+1段网格，步骤如下：

(2)

(3)

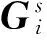
③ 对每一个状态转移，其相应的输出码比特vi为

(4)

或

(5)

其次，对比特级网格进行分段和并行分解以简化网格的构造[2，7]. 以缩短(38，26)BCH码为例，考虑将其比特级网格均匀分成L段，则L的可能取值为38，19和2，其中当L=38时，即比特级网格. 当L=2时，GTOGM中存在有些行的有效时间跨度恰好位于两个分段时刻之间，分段后各时刻状态标记将不携带这些行对应的信息位，最终导致无法对这些信息位进行译码，因此，缩短(38，26)BCH码可行的分段方式只有L=38和L=19. 此外，无论L=38还是L=19，并行分解后网格的最大状态空间维数都超过了并行分解前网格的最大状态空间维数，即不满足并行分解原则[2]，则缩短(38，26)BCH码的L段网格都无法进行并行分解，因此，缩短(38，26)BCH码的可用网格只有L=38和L=19的两种形式.

依据VA译码的译码复杂度，对L=38和L=19时的两种网格进行筛选. 定义VA译码的译码复杂度为NT=NB+NA+NC，其中NB是分支度量次数，NA是加法次数，NC是比较次数，所以具有最小NT的网格是最优网格. 表1统计了L=38和L=19时两种网格的译码复杂度，由表1可知，对于缩短(38，26)BCH码，L=38，即比特级网格的译码复杂度NT最小.

表1 缩短(38，26)BCH码在不同分段方式下的译码复杂度

Tab.1 ECC of differentL-section trellis for shortened (38，26) BCH code

LNBNANCNT38131068131066614393235731912560812560490111341323

2 线性分组码的AVA算法

AVA最早是针对卷积码提出的，在实现线性分组码的最优网格构造后，可以将其应用于线性分组码的译码. 考虑(n，k)线性分组码，其软判决译码采用欧氏距离作为可靠性度量，假设进行Q比特量化，则欧氏距离定义为

(6)

式中:K=2Q-1;v=[v0v1…vn-1]为编码后的码字；c=[c0c1…cn-1]为接收端量化后的码字. 假设(n，k)线性分组码的最优网格是均匀分成L段，每段M个比特，则有L×M=n，第j(1≤j≤L)段网格的分支度量值为

(7)

第i(1≤i≤L)分段点的路径度量值为

(8)

图1给出了线性分组码的AVA译码过程，假设译码过程已经进行到分段点i-1，则分段点i(1≤i≤n)的译码步骤如下.

① 计算第i段所有分支的度量值Bi，如果分支对应的前一分段点状态已被丢弃，则不用计算该分支的度量值.

② 对第i段的每一状态，将该状态的分支度量值Bi和与分支相连的前一状态的幸存路径度量值P(i-1)相加，得到该状态的路径度量值P(i)，即

P(i)=P(i-1)+Bi.

(9)

设置丢弃门限τ，如果P(i)满足

P(i)≤Pmin(i-1)+τ.

(10)

则把其对应的路径保留下来. 如果某一状态的路径都不满足该条件，则丢弃该状态. 最后比较到达该状态的所有满足式(10)的路径，选取具有最小路径度量值的路径为该状态幸存路径.

③ 存储幸存路径及度量值.

④ 比较第i分段点所有状态的幸存路径度量值，选取其中的最小值Pmin(i)用于下一分段点译码.

对后续每一分段点都执行同样的操作，一直到网格末端，即完成了线性分组码的AVA译码过程.

AVA的自适应性在于随着信噪比的变化，丢弃门限值可以进行自适应地调整，使得AVA在保持与VA几乎相同的误码率性能的基础上，可以降低译码复杂度. 当τ→∞时，AVA→VA. 随着τ值的减小，当达到某一最优值τopt时，AVA的误码率性能开始变差；且AVA算法的译码复杂度随着τ值的减小而减小，因此，AVA算法的关键在于确定最佳丢弃门限值τopt.

3 最佳丢弃门限值的估计

用t表示(n，k)线性分组码的纠错能力，未量化的VA可以达到t比特的纠错能力. AVA是对VA的近似，由于使用了丢弃门限τ删除路径和状态，AVA译码时有可能会丢弃正确译码路径，这将导致译码错误. 用Pe，VA表示VA的误字率，则AVA的误字率可以表示为

Pe，AVA=Pe，VA+Ploss.

(11)

其中Ploss是AVA相对VA的译码性能损失，表示正确路径被丢弃的概率.

考虑AWGN信道和BPSK调制的情况，用x=[x0x1…xi…x37]表示发射端的码字序列，则xi=1-2vi∈{1，-1}，接收端码字

r=[r0r1…ri…r37]，

则

ri=xi+ni.

(12)

其中ni～N(0，σ2).

y=[y0y1…yi…y37]表示BPSK解调后的序列，则

yi=(1-ri)/2=vi-ni/2.

(13)

其中yi～N(vi，σ2/4).

令c=[c0c1…ci…c37]为解调后的硬判决序列，ci∈{0，1}. 由此可得到接收序列c中每个比特的错误概率为

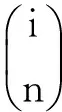
考虑在Ei种错误类型中有Ni种是VA可以正确译码的，则由于i个比特错误，导致AVA译码失败而VA译码正确的概率可以表示为

通常情况下Pb较小，可认为Pb→0，则(1-Pb)→1，故式(16)可简化为

假设当硬判决序列c中错误比特的个数小于等于硬判决的丢弃门限τhard时，VA和AVA都可以正确译码，随着错误比特数i的增加，当i≥t+1时，Ni将非常小，所以Ploss可表示为

(18)

当τhard=t时，

因为Pb通常很小，式(19)的结果通常取决于Pb的大小，因此，Ploss可进一步近似为

下面考虑VA和AVA都进行软判决译码的情况，硬判决译码可看作1比特量化的软判决译码的特殊情况. 将上述硬判决译码的结论推广到软判决译码的情况下，Ploss仍然满足式(18)～(20)，区别在于硬判决译码时分析的是汉明距离，即错误比特数i，软判决译码时分析的是欧氏距离dE.

对于软判决的情况，假设当软判决量化后序列c与码字序列v的欧氏距离小于等于软判决的丢弃门限τsoft时，VA和AVA都可以正确译码，随着欧氏距离dE的增加，当dE≥(t+1)K时，导致AVA译码失败而VA译码正确的概率PdE将非常小，所以Ploss可表示为

其中K=2Q-1，Q为软判决的量化比特数. 类似地，当τsoft=[(t+1)K-1]时，Ploss满足式(20).

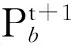
τhard=t±ε.

(22)

或者

τsoft=[(t+1)K-1]±ε.

(23)

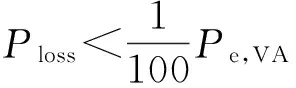
以缩短(38，26)BCH码为例，其纠错能力t=2，当该码采用3比特均匀量化时，由式(23)可得τsoft=20±ε. 表2中给出了不同信噪比SNR下的Pe，VA和Ploss，因为Eb/N0(dB)=10lgEb/N0=10lg1/(2σ2)，则

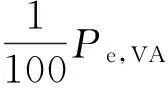
表2 不同SNR下的Pe，VA和Ploss统计

图2给出了缩短(38，26)BCH码在Eb/N0=0～4 dB下，AVA的误字率随着丢弃门限τsoft变化的性能曲线，为便于比较，图中也标出了VA的误字率. 根据以上分析，τsoft=20-ε，因此，τsoft以2为间隔，在区间内取整数值. 从图2可以看出，当AVA的误字率RWE接近VA的RWE时，对应的τsoft的值即最佳丢弃门限的值. 统计得到的缩短(38，26)BCH码在不同SNR下的最佳丢弃门限值τopt如表3所示.

表3 缩短(38，26)BCH码在不同SNR下对应的τopt值

Tab.3 Estimated optimal threshold for different SNR from simulation results for shortened (38，26) BCH code

(Eb/N0)/dB01234τopt1818171614

4 仿真结果及分析

图3给出了AVA、VA和Chase-2算法的WER性能曲线，其中AVA算法在不同SNR下的丢弃门限值如表3所示. 从图3可看出，在任意SNR条件下， AVA和VA的WER性能都十分接近，Chase-2算法的WER性能较差，这是因为Chase-2算法是一种次优的译码算法，而VA实现了最大似然译码，是一种最优的译码算法，AVA又是VA的近似. BER性能曲线有着相同的趋势.

不同τ值的AVA的译码复杂度不同，采用ACS单元使用数目作为译码复杂度的衡量指标. VA和AVA的ACS单元使用数目与SNR的关系曲线如图4所示，可知，当Eb/N0=0～4 dB时，AVA的ACS单元使用数目分别是VA的26%、26%、19%、11%和5%，即随着SNR的增大，AVA译码过程中利用的ACS单元数目相比VA的减小程度愈加明显.

5 结 论

本文针对伽利略搜救系统中的缩短(38，26)BCH码，提出了一种自适应维特比译码算法(AVA). 该算法基于缩短(38，26)BCH的最优网格，在VA的基础上，增加了一个丢弃门限，丢弃门限值的大小随着信噪比而发生变化，以保证AVA和VA具有相同的误码率性能的条件下，尽可能地降低译码复杂度. 此外，文中还给出了丢弃门限值的估计方法，并确定了各个信噪比下的最佳丢弃门限值. 仿真结果表明，AVA在保持与VA相同的误码率性能的基础上，在Eb/N0=0～4 dB时，AVA的ACS单元使用数目分别是VA的26%、26%、19%、11%和5%.

本文提出的丢弃门限值的估计方法在推导的过程中有近似，所以实际的丢弃门限值要在此基础上进行修正，文中通过仿真给出了修正后的丢弃门限值，并没有从理论上分析修正量的大小，这是作者后续要进一步研究的问题. 此外，文中所研究的缩短(38，26)BCH码并不适合做并行分解，因此，所研究的AVA算法也没有涉及到并行分解问题，对并行分解的网格进行AVA译码也是作者后续要进一步研究的问题.

[1] Cospas-Sarsat Council. Specification for COSPAS-SARSAT 406 MHz distress beacons (Revision 13)[S]. [S.l.]: COSPAS-SARSAT, 2012.

[2] Lin S, Costello Jr D J. Error control coding[M]. 2nd ed. New Jersey: Pearson Prentice-Hall， 2004.

[3] Zhang D S， An J P， Fan Y Y. Improved Berlekamp-Massy algorithm and its software implementation on DSP[J]. Journal of Beijing Institute of Technology (English Edition)， 2010，19(2):207-210.

[4] Liu X J， Zhao C M， Sun X J. Low complexity Chase-2 decoding of concatenated codes[J]. Chinese Science Bulletin， 2010，55(26):3066-3070.

[5] Wolf J K. Efficient maximum likelihood decoding of linear block codes using a trellis[J]. IEEE Transactions on Information Theory， 1978，24(1):76-80.

[6] Forney Jr G D. Coset codes-part II: binary lattices and related codes[J]. IEEE Transactions on Information Theory， 1988，34(5):1152-1187.

[7] Moorthy H T， Lin S， Uehara G T. Good trellises for IC implementation of Viterbi decoders for linear block codes[J]. IEEE Transactions on Communications， 1997，45(1):52-63.

[8] Forney Jr G D， Gluesing-Luerssen H. Codes on graphs: observability， controllability， and local reducibility[J]. IEEE Transactions on Information Theory， 2013，59(1):223-237.

[9] Gluesing-Luerssen H， Forney Jr G D. Local irreducibility of tail-biting trellises[J]. IEEE Transactions on Information Theory， 2013，59(10):6597-6610.

[10] Naguib A F， Seshadri N， Calderbank A R. Increasing data rate over wireless channels[J]. IEEE Signal Processing Magazine， 2000，17(3):76-92.

[11] Chan F， Haccoun D. Adaptive Viterbi decoding of convolutional codes over memoryless channels[J]. IEEE Transactions on Communications， 1997，45(11):1389-1400.

[12] Suganya G S， Kavya G. RTL design and VLSI implementation of an efficient convolutional encoder and adaptive Viterbi decoder[C]∥International Conference on Communications and Signal Processing (ICCSP). Melmaruvathur， India:[s.n.]， 2013:494-498.

[13] Brahmbhatt C， Mishra M. Design and implementation of adaptive Viterbi decoder for high speed applications[J]. International Journal of Advanced and Innovative Research， 2013，11(2):340-343.

[14] Sonar N S， Al-Naimy F S， Mudholkar R R. An improved dynamically reconfigurable pipelined adaptive viterbi decoder for high throughput[J]. International Journal of Engineering and Innovative Technology， 2013，7(2):194-198.

(责任编辑：刘芳)

Adaptive Viterbi Decoding Algorithm for the Shortened (38,26) BCH Code Based on Trellis

HOU Shu-juan， SONG Ling-yan， SUN Lin

(School of Information and Electronics， Beijing Institute of Technology， Beijing 100081， China)

Galileo search and rescue system (Galileo/SAR) adopts the shortened (38,26) BCH code in its physical layer protocol. In this paper, an adaptive Viterbi decoding algorithm (AVA) was proposed. The best trellis for the shortened (38,26) BCH code was first presented. In the AVA, a discarding threshold was designed on the basis of the Viterbi algorithm (VA), only retaining the most likely paths. The discarding threshold could vary with the different SNR and be adjusted adaptively to reduce the decoding complexity as much as possible, with almost the same error performance as the VA. Simulation results show that, the decoding complexity of the AVA reduces greatly compared with the VA, maintaining nearly the same error performance. Especially at high SNR, the decoding complexity decreases more obviously.

AVA; discarding threshold; shortened BCH code; Galileo SAR system

2014-09-02

侯舒娟(1977—)，女，博士，副研究员，E-mail:shujuanhou@bit.edu.cn.

TN 967.1

A

1001-0645(2016)11-1205-06

10.15918/j.tbit1001-0645.2016.11.020