考虑摩擦的两球体接触承载分析的分形接触模型研究
2016-12-17晏伟清
樊 浩, 晏伟清, 刘 鹏, 陈 奇
(合肥工业大学 机械与汽车工程学院,安徽 合肥 230009)
考虑摩擦的两球体接触承载分析的分形接触模型研究
樊 浩, 晏伟清, 刘 鹏, 陈 奇
(合肥工业大学 机械与汽车工程学院,安徽 合肥 230009)
为了获得更贴合实际的两球体接触承载能力分析的分形接触模型,文章考虑摩擦的影响,在两球体接触应力计算分形模型的基础上,引入存在摩擦的弹塑性变形临界面积公式,给出考虑摩擦的两球体分形接触模型;通过在Matlab中对模型的仿真和预测,获得了模型中主要参数对两球体接触承载能力的影响。结果表明:降低摩擦系数、减小粗糙度幅值以及选择内接触形式,有利于提高接触承载能力;分形维数与接触承载能力之间不是一个简单的线性关系,而是存在一个分形维数的最优值。因为球面副是球轴承的简化模型,所以该文的研究为后续进行球轴承及相关产品的接触承载分析提供了理论依据。
摩擦球面副;接触承载分析;分形理论
高副接触体之间的表面承载能力是影响其强度和寿命的重要指标。目前,用于高副接触体间的表面承载能力分析主要有传统的Hertz方法[1]、近现代的有限元方法[2-6]以及近年来比较热门的分形理论方法[7-8]。前两者主要用于宏观分析,而后者可进行微观分析,能分析接触体表面微观形貌对接触承载的影响,因此考虑因素更全面,分析能力更强,从而得到了研究者们的广泛关注[9-13]。
齿轮和轴承为常见的高副接触体产品。具体分析时,常常把齿轮副接触和圆柱滚子轴承简化为两圆柱体,把球轴承简化为两球体。目前,关于两圆柱体和齿轮的分形承载能力分析已经取得了一定的成果[14-17];对于两球体的分形接触承载能力分析也进行了前期研究,并建立了基于分形理论的两球体接触模型[18],但是该模型没有考虑摩擦对接触承载能力的影响。在实际工况中,摩擦常常不可忽略,因此,需要建立更为准确的两球体接触承载能力分析的分形接触模型,并将之用于球面副相关产品的接触应力分析。
本文以M-B分形接触模型和两球体分形接触模型为基础,引入存在摩擦的弹塑性变形临界面积公式,给出考虑摩擦的两球体分形接触模型;通过对该模型的预测分析可以获得相关参数对其承载能力影响的变化规律,有利于提高其接触承载能力的最优参数,为改善和提高球面副及相关产品的接触承载能力提供理论依据。
1 考虑摩擦的两球体分形接触模型
在M-B分形接触模型的基础上,结合两球体的接触面积分布公式和考虑摩擦的弹塑性临界接触面积公式,得出考虑摩擦因素的两球体接触承载能力的分形接触模型。
1.1 M-B分形接触模型
文献[19]建立了粗糙表面的弹塑性接触的分形模型,即M-B分形接触模型。M-B分形接触模型给出了粗糙“平面”间的接触载荷与实际接触面积之间的关系,其公式描述如下。
(1) 当al>ac,接触点发生弹塑性变形,则总载荷为:
(1)
其中,第1项为弹性接触载荷;第2项为塑性接触载荷。
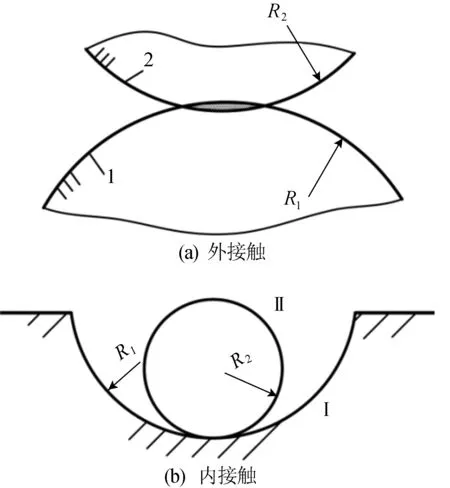
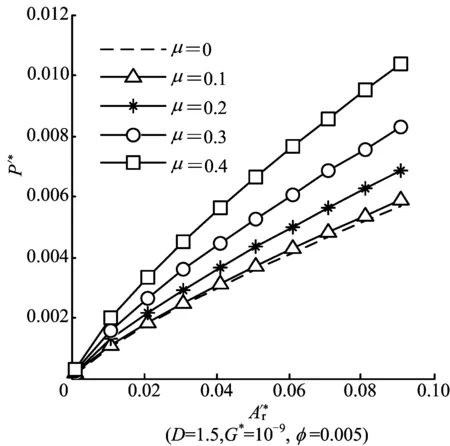
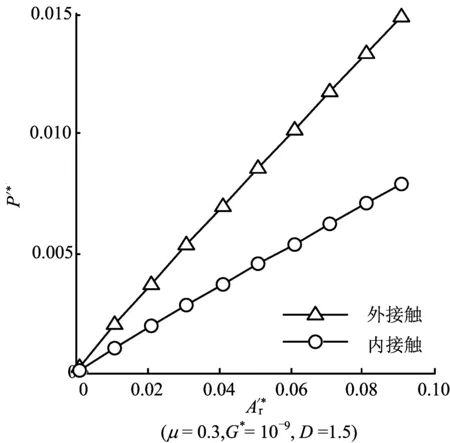
(2) 当al (2) (3) as为最小接触点的面积;al为最大接触点的面积;ac为微凸体弹塑性变形临界面积,其计算公式为: (4) 其中,φ为材料的特性参数,定义φ=σy/E。 1.2 两球体的接触面积分布公式 M-B分形接触模型主要分析粗糙“平面”间的接触承载能力,而对于粗糙“曲面”间的接触问题未能涉及。为了将M-B分形接触模型应用于粗糙曲面,本研究团队经过研究建立了“两任意轮廓弹性体接触应力计算的分形模型”[21],并同时建立了“两球体的分形接触模型”[18]。在上述模型中,引入了表面接触系数,对接触面积分布公式进行了修正,从而解决了M-B不能分析粗糙“曲面”间的接触承载问题。已获得的“两球体的接触面积分布”计算公式如下: (5) 其中,λB为两球体的接触系数,其计算公式[16]为: (6) 其中,R1和R2为两圆柱体的曲率半径;“+”为外接触;“-”为内接触(假设R1>R2)。 两球体接触示意图如图1所示。 图1 两球体接触示意图 1.3 考虑摩擦的弹塑性临界接触面积计算公式 根据文献[22]的研究可知,存在摩擦时微凸体弹塑性变形临界面积的计算公式为: (7) 其中,aμc为考虑摩擦的微凸体弹塑性变形临界面积;kμ为摩擦力修正因子,与摩擦系数μ有关,其计算公式为: (8) 1.4 考虑摩擦因素的两球体分形接触模型 将(5)式和(7)式带入M-B分形接触模型,即可得到“考虑摩擦因素的两球体分形接触模型”,该模型可建立两球体接触载荷与真实接触面积之间的关系。具体公式描述如下。 (1) 当al>aμc时,接触点处于弹塑性接触状态,此时又分成如下2种情况: 当D≠1.5时,有 (9) 当D=1.5时,有 (10) (11) (2) 当al (12) 为了验证上述模型,本文在Matlab中对模型进行仿真,重点分析模型中的4个主要参数(摩擦系数、分形维数、粗糙度幅值以及接触形式)对两球体接触承载能力的预测分析。 假设两球面副的基本参数如下:弹性模量E1=E2=2.06×105N/mm2,泊松比υ1=υ2=0.3,球体半径分别为R1=100 mm,R2=60 mm。 2.1 摩擦系数对两球体承载能力的影响 摩擦系数对两球体接触承载的影响如图2所示。由图2可知,随着摩擦系数μ的增加,相同真实接触面积对应的法向载荷增加,接触应力增加,从而接触承载能力下降。 这一结论与实际经验相符,即降低接触体的摩擦(如常采用润滑措施)对于提高接触面的承载能力有利,也与文献[23-24]中的试验结果一致,因此上述模型可信。 图2 摩擦系数对两球体接触承载的影响 2.2 分形维数对两球体承载能力的影响 分形维数对两球体接触承载的影响如图3所示。 图3 分形维数对两球体接触承载的影响 由图3可知,分形维数对两球体承载能力的影响,不是一个简单的线性关系,而是存在一个最优值,即随着分形维数的增加,接触承载能力总体趋势为增强。但当分形维数为1.5时,相同载荷时的真实接触面积最大,因此此时的接触应力最小,接触承载能力最强。 这一结论的总体趋势与文献[25]的结论一致,即分形维数与表面粗糙度大体成负指数关系,即减小表面粗糙度,分形维数增加,表面承载能力提高。但由于分形维数与表面粗糙度并非一一对应关系[25],因此降低表面粗糙度,并不一定提高分形维数,即不一定对提高表面承载能力有利。本文仿真结果也反映了该问题,即分形维数对两球体的接触承载能力影响并非是简单的线性关系,而是存在一个最优值。鉴于篇幅,分形维数的优化理论研究本文不再赘述。 2.3 粗糙度幅值对两球体承载能力的影响 粗糙度幅值对两球体接触承载的影响如图4所示。由图4可以看出,随着粗糙度幅值的降低,相同真实接触面积的法向载荷也降低,因此减小粗糙度幅值对于提高两球体之间的接触承载能力有利。 由文献[16]可知,粗糙度幅值G*是反映表面粗糙度的参数,且两者成正比关系。即减小粗糙度幅值,表面粗糙度随之降低,表面承载能力可相应提高。由以上分析可知,上述结论与实际经验和已有的结论一致,因此结论可信。 图4 粗糙度幅值对两球体接触承载的影响 2.4 接触形式对两球体承载能力的影响 接触形式对两球体接触承载的影响如图5所示。由图5可知,内接触时比外接触时的承载能力要高,因此尽量选用内接触的高副产品可降低接触应力,改善接触条件。 这一结论与Hertz理论对于接触形式的分析一致[26-27]。因此上述结论合理。 图5 接触形式对两球体接触承载的影响 本文考虑摩擦因素的影响,通过引入存在摩擦的弹塑性变形临界面积公式,并结合两球体接触面积分布公式,建立了考虑摩擦的两球体分形接触模型。通过对模型的仿真和预测,得到了模型中主要参数对两球体接触承载能力影响分析的主要结论:① 摩擦系数与两球体表面承载能力成反比关系,即随着摩擦系数的降低,有利于提高两球体的接触承载能力;② 分形维数与两球体的表面承载能力大体成正比关系,但并非是一个线性关系,而是存在一个分形维数的最优值。因此,对于特定工况,需要进行分形维数的优化设计;③ 粗糙度幅值与两球体的表面承载成正比关系,即降低粗糙度幅值有利于提高表面承载能力;④ 内接触时比外接触时的球面副表面应力要低,因此尽量选用内接触的结合形式。 [1] BHUSHAN B.Introduction to tribology[M].New York:John Wiley & sons Ltd,2002. [2] 张卧波.有限元法计算齿轮接触强度的理论研究[J].农业机械学报,1999,30(3):89-92. [3] 邓效忠,方宗德,杨宏斌.准双曲面齿轮齿面接触应力过程计算[J].中国机械工程,2001,12(12):1362-1364. [4] 刘晖,万朝燕,谢素明,等.基于I-DEAS的齿轮接触强度分析[J].现代制造工程,2005 (1):102-103. [5] 武丽.有限元分析法及其软件在齿轮接触强度分析中的应用[J].机械管理开发,2007(2):74-75. [6] 李凤吉.双渐开线齿轮接触强度分析及试验研究[D].合肥:合肥工业大学,2008. [7] 杨生华,王统.齿轮轮齿变形中的接触有限元仿真分析[J].煤矿机械,1999(8):9-11 [8] 杨生华.齿轮接触有限元分析[J].计算力学学报,2003,20(2):189-194. [9] 陈国安,张晓云,葛世荣.分形理论及其在工程机械中的应用前景[J].建筑机械,1999(1):47-51. [10] 史立新.分形理论在机械加工表面分析中的应用[J].农机化研究,2000(2):112-114. [11] MAJUMDAR A,BHUSHAN B.Role of fractal geometry in roughness characterization and contact mechanics of surfaces[J].Journal of Tribology,1990,112(2):205-216. [12] BHUSHAN B,MAJUMDAR A.Elastic-plastic contact model for bifractal surfaces[J].Wear,1992,153(1):53-64. [13] MAJUMDAR A,SUGIMUTR J.Characterization and contact mechanics of fractal and non fractal surfaces[J].Toraibarojisuto/Journal of Japanese Society of Tribologists,1995,40(7):539-544. [14] 黄康,赵韩,陈奇.两圆柱体表面接触承载能力的分形模型研究[J].摩擦学学报,2008,28(6):529-533. [15] HUANG K,ZHAO H,CHEN Q.Research on fractal contact model of cylinders’ surface[M]//Advanced Tribology.Berlin Heidelberg:Springer,2009:548-553. [16] 陈奇.基于分形理论的汽车变速箱齿轮接触强度研究[D].合肥:合肥工业大学,2010. [17] 陈奇,赵韩,黄康,等.分形理论在齿轮接触应力分析中的应用研究[J].中国机械工程,2010,21(9):1014-1017,1057. [18] ZHAO H,CHEN Q,HUANG K.Analysis of two ball's surface contact stress based on fractal theory[J].Materials Science Forum,2011,675/676/677:619-627. [19] 葛世荣,朱华.摩擦学的分形[M].北京:机械工业出版社,2005. [20] MAJUMDAR A,BHUSHAN B.Fractal model of elastic-plastic contact between rough surfaces[J].ASME Journal of Tribology,1991,113(1):1-11. [21] 陈奇,黄康,张彦,等.两任意轮廓弹性体接触应力计算的分形模型研究[J].机械强度,2012,34(4):557-561. [22] 李小彭,王伟,赵米鹊,等.考虑摩擦因素影响的结合面切向接触阻尼分形预估模型及其仿真[J].机械工程学报,2013,48(23):46-50. [23] 肖乾,王成国,周新建,等.不同摩擦系数条件下的轮轨滚动接触特性分析[J].中国铁道科学,2011,32(4):66-71. [24] 夏延秋,丁津源,马先贵,等.摩擦系数对齿轮接触疲劳寿命的影响[J].机械传动,2002,26(1):48-49. [25] 葛世荣,Tonder K.粗糙表面的分形特征与分形表达研究[J].摩擦学学报,1997,17(1):73-80. [26] JOHNSON K L.Contact mechanics[M].Cambridg,Eng.:Cambridge University Press,1987. [27] 濮良贵,纪名刚.机械设计[M].8版.北京:高等教育出版社,2007. (责任编辑 胡亚敏) Research on fractal contact model for contact carrying capacity of spherical pair considering friction factor FAN Hao, YAN Weiqing, LIU Peng, CHEN Qi (School of Machinery and Automobile Engineering, Hefei University of Technology, Hefei 230009, China) In order to set up a more realistic fractal contact model of spherical pairs for contact carrying capacity analysis, the fractal contact model of spherical pairs considering the factor of friction is deduced by introducing the equation of calculating critical contact area of elasto-plastic deformation with friction and referring to an earlier fractal contact model of spherical pairs. By the simulation and prediction in Matlab, the influence of some parameters in the model on the contact carrying capacity is acquired. The numerical results show that reducing the friction coefficient, decreasing the roughness amplitude and choosing the style of inner contact can help to improve the contact carrying capacity; the relationship between fractal dimension and contact carrying capacity is not simply linear, but there is an optimal value of fractal dimension. Because the spherical pair is a simplified model for ball bearing, the presented research can lay a theoretic basis for the contact carrying capacity analysis of ball bearings and related products. friction spherical pair; contact carrying capacity analysis; fractal theory 2015-06-17; 2015-07-22 国家自然科学基金资助项目(51305116) 樊 浩(1993-),男,安徽肥东人,合肥工业大学硕士生; 陈 奇(1979-),男,安徽肥东人,博士,合肥工业大学副教授,硕士生导师. 10.3969/j.issn.1003-5060.2016.11.006 TH114 A 1003-5060(2016)11-1468-05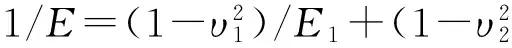

2 模型仿真与预测


3 结 论
