基于LabVIEW数字PID直流电机调速系统的实现

施尚英

（四川职业技术学院电子电气工程系,四川　遂宁　629099）

基于LabVIEW数字PID直流电机调速系统的实现

施尚英

（四川职业技术学院电子电气工程系,四川遂宁629099）

该文介绍了直流电机的数学模型分析及利用传统方法建立直流电机模型与传递函数的建立方法，并简要介绍了PID控制原理及参数对控制性能的影响.根据直流电机传递函数与离散系统的PID函数关系，利用LabVIEW实现PID直流电机调速系统实现方法，最后给出了数字PID控制的LabVIEW程序图实现数字PID直流电机调速.

数字PID；直流电机；传递函数；离散；LabVIEW

PID（比例P-积分I-微分D）控制器是一个在工业闭环控制系统应用中常见的一种模糊自动控制算法，具有原理简单、适用性广、鲁棒性好、控制参数相互独立和可靠性高等特点.本文以直流电机调速系统为例，介绍了直流电机的数学模型分析及利用传统方法建立直流电机模型与传递函数的建立方法，分析推到并给出直流电机调速系统传递函数，以及带PID控制的系统框图，简单介绍了离散PID参数的整定方法，连续PID参数到离散化PID方程，最终通过LabVIEW虚拟仪器实现高效、快速、稳定的直流电机调速控制.

1　直流电机的数学模型

直流电机是现今工业上应用最广的电机之一，直流电机具有良好的调速特性、较大的启动转矩、功率大及响应快等优点.

为实现快速可靠的数字PID直流电机调速系统控制，在系统设计中常通过建立直流电机数学模型的方式来分析并计算相关参量.

建立直流电机数学模型的基础是直流电机的机械特性方程和电气方程，对直流电机的电气方程、直流电机的机械方程进行拉普拉斯变化即可得直流电机的转速相对于输入电压的传递函数与电动机的数学模型.

上式中La为电枢电感（H），ia为电枢电流（A），ua为电枢电压（V），ra为电枢电阻（Ω），Ce为电机电动势系数.

上式中T、TL为电动机转矩和负载阻转矩，其中T=Ctia，J为折算到电动机轴上的转动惯量.

对直流电机的电气方程、直流电机的机械方程进行拉普拉斯变化得到（3）式.

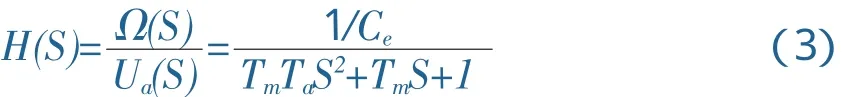
（3）式为直流电机转速相对于输入电压的传递函数式为，式中Tm为直流电机的机械时间常数，其公式关系为Tm=JRaCeCT；Ta为直流电机电气时间常数，其公式关系为Ta=LaRa.

直流电机的传递函数是一个二阶无滞后传递函数。二阶无滞后传递函数的数学模型：

由于Ta＜＜Tm，所以近似认为Tm+Ta≈Tm，k=1Ce。

对于（4）式，输入幅度为a的阶跃信号，阶跃信号的时域相应为：

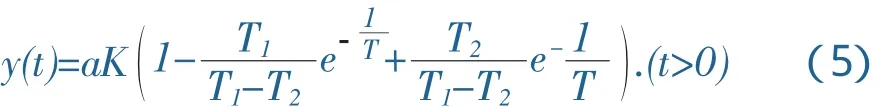
2　利用传统方法求解直流电机模型参数

直流电机一般包含磁极、电枢和电刷3个部分组成.其电气结构如图1所示.在分析计算中一般采用工程估算方法分析技术直流电机的模型参数.直流电机机械结构与电路模型图如图1所示.根据直流电机的转速相对于输入电压的传递函数与电动机的数学模型，结合图2.1所示直流电机模型图与工程设计估算方法可以得到直流电机模型相关参量估算公式：

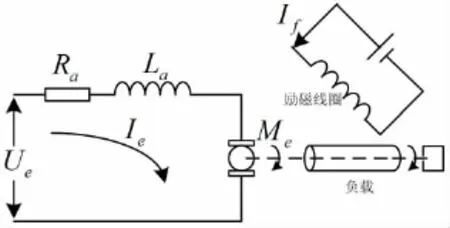
图1　直流电机模型图

式（8）中p为磁极对数

例如某一直流电机的主要参数为额定工作电压220V、额定工作电流10.0A、额定输出功率1.9KW、转动惯量0.027J·S2、额定转速377 rad/s.

利用直流电机模型参数的经验公式，可得Ra= 1.5Ω，Ce=0.56V.s/rad，La=0.235H，Me=5.3N.m，CT=0.51N.m/A，Ta=0.0129s，Tm=0.13Ss.

将Tm、Ta、Ce代入（3）式可得该直流电机的传递函数为：

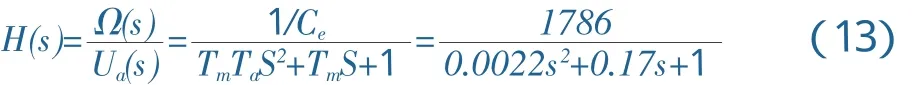
3　PID控制原理及参数对控制性能的影响

PID控制器是一个在工业闭环控制系统应用中常见的一种模糊自动控制算法，直流电机PID控制系统原理框图如图2所示，该闭环控制系统主要由控制目标给定值输入信号rin（t）、反馈检测变送信号f（t）、控制偏差（净输入信号）e（t）、PID（比例P-积分I-微分D）控制器、PID线性组合构成被控对象控制量u（t）、被控对象等及部分组成.

通过转速计对被控对象直流电机的当前转速进行检测处理后，经过反馈网络送入到控制偏差处理模块与控制目标给定值进行误差计算，然后经过比例P、积分I、微分D运算与PID线性组合得带电机转速误差控制量，修正电机当前转速并最终实现电机当前转速与给定的电机转速保持一致.

PID控制器的控制偏差e（t）与输出对象控制量u（t）关系为：

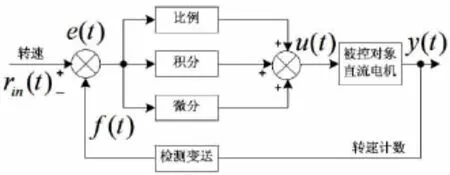
图2　直流电机PID控制系统原理框图

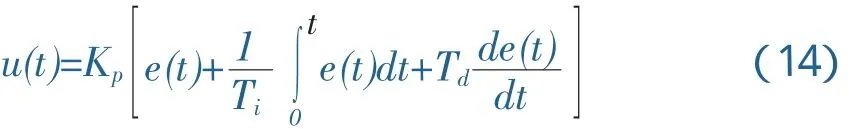
式中u（t）是被控对象（直流电机）输入控制量，e（t）是控制偏差，Kp为PID控制器的比例系数，Ti为PID控制器的积分速度，Td为PID控制器的微分时间常数.

采用PID控制器的直流电机控制系统框图如图2所示.由PID控制器的输入输出关系，如式（14）所示，可得到直流电机PID控制系统传递函数，其传递函数为：

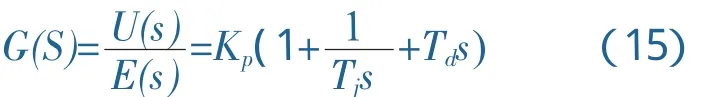
由式（15）可见直流电机PID控制系统的比例、积分和微分三个控制环节相对独立，在控制过程中改变比例、积分和微分单一参量规律可实现分别控制，也可同时改变多个参量实现多种规律控制.在PID控制器的比例、积分和微分控制各环节的主要特性为：

（1）比例环节P

在P调节中，调节器的输出信号u（t）与偏差信号e（t）成比例，即u（t）=Kp.e（t），其中Kp称为比例增益. Kp在较大时，偏差e（t）仅在一定的范围内与控制器的输出保持线性关系.因此，比例控制有一定的应用范围，超过该范围时，控制器输出与输入之间不成比例关系，存在稳态误差.

（2）积分环节I

（3）微分环节D

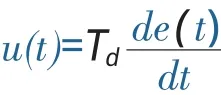
4　数字PID

连续PID经数字离散化处理得到数字PID，数字PID控制比连续PID控制更为优越，因为计算机程序的灵活性，很容易克服连续PID控制中存在的问题，经修正而得到更完善的数字PID算法.数字化PID常见的有位置式PID控制算法、增量式PID控制算法两大类.

实现数字PID的方法是将连续系统的微分方程应由相应的描述离散系统的差分方程来代替。离散化时，令

则有

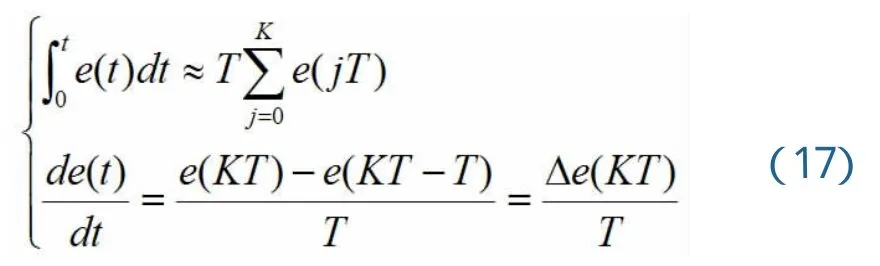
式中，e(KT)是第K次采样所获得的偏差信号；△e(KT)是本次和上次测量值的偏差，在给定值不变时，△e(KT)可表示为相邻两次测量值之差e(KT) -e(KT-T)；T是采样周期，采样周期必须足够短，才能保证有足够的精度；K是采样序号，K=0,1,2….

则离散系统的PID算式为：

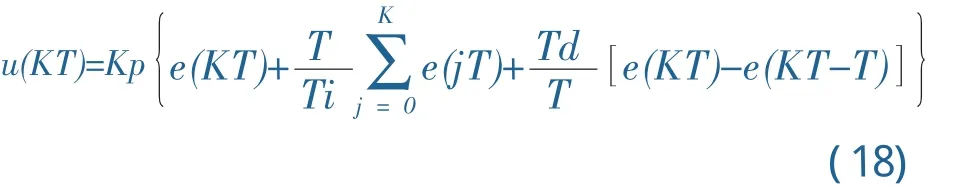
在上式中所表示的控制算式中，其输出值与阀位是一一对应的，通常称为PID的位置算式.在位置算式中，每次的输出与过去的所有状态有关.

5　LabVIEW程序实现

LabVIEW是由美国国家仪器（NI）公司研制开发的图形化编辑语言G编写程序开发环境，在测试测量、工控控制、数学建模仿真等领域应用较为广泛.基于LabVIEW实现数字PID直流电机调速系统的程序流程图如图3所示.

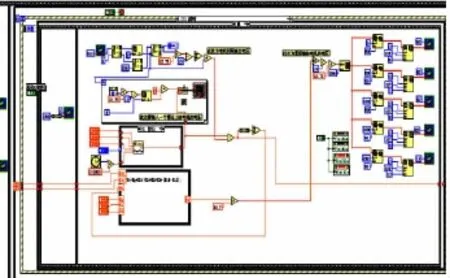
图3　LabVIEW数字PID直流电机调速系统

6　结束语

本文重点介绍了数字PID算法在直流电机调速上实现的流程.根据直流电机传递函数与离散系统的PID函数关系，利用LabVIEW实现PID直流电机调速系统实现方法，最后给出了数字PID控制的LabVIEW程序图实现数字PID直流电机调速.

[1]孙亮,杨鹏.自动控制原理[M].北京:北京工业大学出版社,2006.

[2]雷振山,肖成勇.LabVIEW高级编程与虚拟仪器工程应用[M].北京:中国铁道出版社,2009.

[3]郑对元.LabVIEW虚拟仪器程序设计[M].北京:清华大学出版社,2012.

[4]岂兴明,田京京,夏宁.LabVIEW入门与实战开发100列[M].北京:电子工业出版社,2011.

[5]雷振山,肖成勇,魏丽，等.LabVIEW高级编程与虚拟仪器工程应用[M].北京:中国铁道出版社,2012.

责任编辑：张隆辉

TM33

A

1672-2094（2016）04-0174-03

2016-05-02

施尚英（1980-）,女,四川简阳人，四川职业技术学院讲师，硕士.研究方向：电气自动化，电子技术.