带电粒子在匀强磁场作匀速圆周运动的求解策略
2016-12-16郭文教
郭文教●
金华汤溪高级中学(321075)
带电粒子在匀强磁场作匀速圆周运动的求解策略
郭文教●
金华汤溪高级中学(321075)
策略一 充分利用平面几何中圆的有关知识找圆心
带电粒子在匀强磁场中的匀速圆周运动往往需画出示意图,找几何关系,而找出圆心是解决此类问题的前提.利用圆的知识找圆心通常有以下几种方法.
1.在已知粒子运动轨迹上的两点速度方向的情况下找圆心.方法是:画出粒子轨迹上两点(一般是射入和射出磁场 的两点)洛伦兹力的方向(与速度方向垂直),洛伦兹力延长线的交点即为圆心.
2.在已知粒子运动轨迹的两点和其中一点的速度方向的情况下找圆心.方法是:画出轨迹上两点间的连线(即过这两点圆弧的弦)做它的中垂线,画出已知点速度v的垂线,中垂线与速度垂线的交点即为圆心.
3.在已知粒子轨迹上两点和能够求得半径R值的情况下找圆心.方法是:连接粒子轨迹上的两点,并做连线的中垂线,连线端点到中垂线距离为半径R的点即为圆心.
4.在已知带电粒子入射方向和出射方向,且能够求得粒子轨迹半径R,但不知粒子轨迹的情况下找圆心.方法是:延长粒子两速度方向的直线,做直线所成夹角的角平分线,从角平分线到两直线的垂直距离等于半径R的点即为圆心.
例1 如图1所示,一带电质点,质量为m,电量为q,以平行于Ox轴的速度v从y轴上的a点射入图1中第一象限所示的区域.为了使该质点能从x轴上的b点以垂直于Ox轴的速度v射出,可在适当的地方加一个垂直于xy平面、磁感应强度为B的匀强磁场.若此磁场仅分布在一个圆形区域内,试求这圆形磁场区域的最小半径.重力忽略不计.
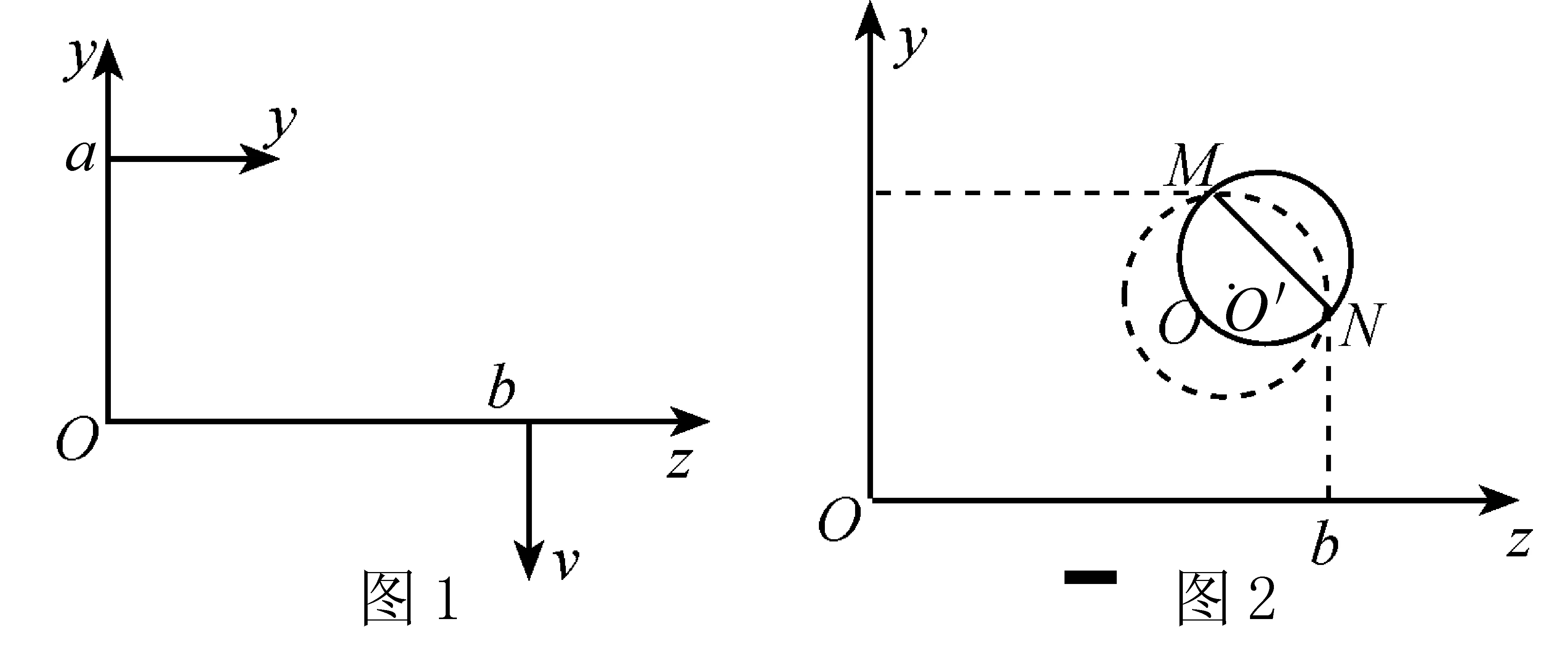
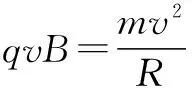
根据题意,质点在磁场区域中的轨道是半径等于R的圆上的1/4圆周,这段圆弧应与入射方向的速度、出射方向的速度相切.如图2所示,过a点作平行于x轴的直线,过b点作平行于y轴的直线,则与这两直线均相距R的O′点就是圆周的圆心.质点在磁场区域中的轨道就是以O′为圆心、R为半径的圆(图中虚线圆)上的圆弧MN,M点和N点应在所求圆形磁场区域的边界上.
在通过M、N两点的不同的圆周中,最小的一个是以MN连线为直径的圆周.所以本题所求的圆形磁场区域的最小半径为:
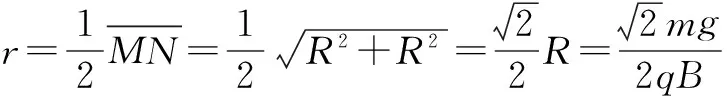
策略二 充分利用示意图中的几何关系找半径
在找到圆心后,建议大家在解题时可不管三七二十一先在草稿纸上画一个完整的圆,然后分析原题中入射粒子的洛伦磁力,确定粒子的运动轨迹朝哪边弯(顺时针还是逆时针),再将其与我们画好的圆相对照,根据题目的意思看题中的轨迹是落在这个完整圆中的哪一部分,逐渐完善.等画好示意图后,能否充分利用好示意图中的几何关系,找到半径的表达式是解决问题的关键.
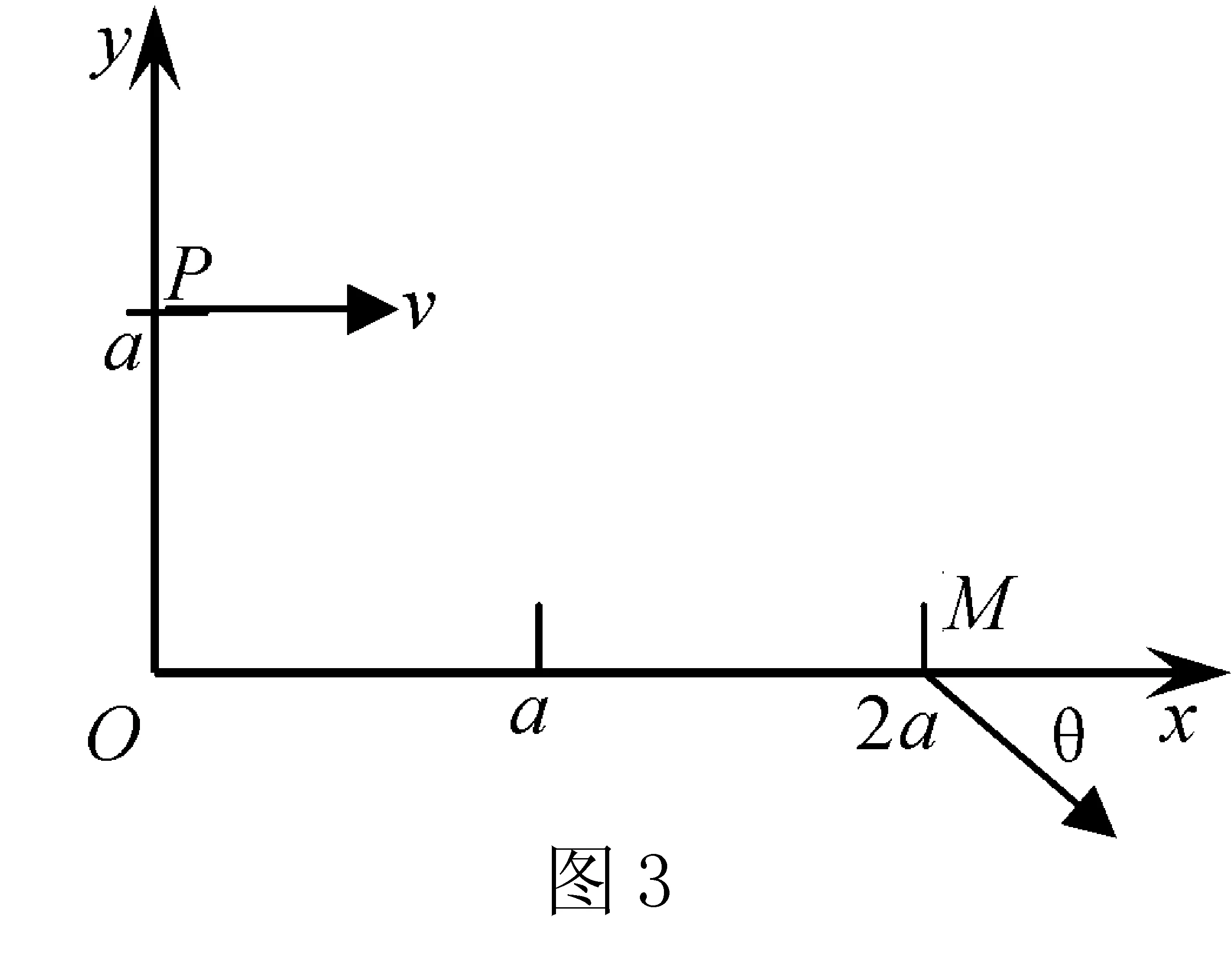
例2 电量为q、质量为m的带正电粒子在XOY平面内沿着Y=a的直线以速度v经Y轴上的P点射入XOY平面的第一象限.要求在第一象限内设置磁感应强度为B的一个圆形区域,使带电粒子发生偏转,最后经X轴上的M点(XM=2a)射出,且偏转角θ=60°,如图3所示.试求能达到此目的的最小圆形磁场区域的半径(粒子的重力不计).
解析 依题意,磁场的方向垂直纸面向外.由于带电粒子的速度和磁场都是确定的,所以带电粒子作圆周运动的半径r=mv/qB也是确定的.将X轴和Y轴上的两个速度矢量(或反向)延长,与X、Y轴组成一个梯形,再画一个半径确定的圆(轨迹),并将此圆移至坐
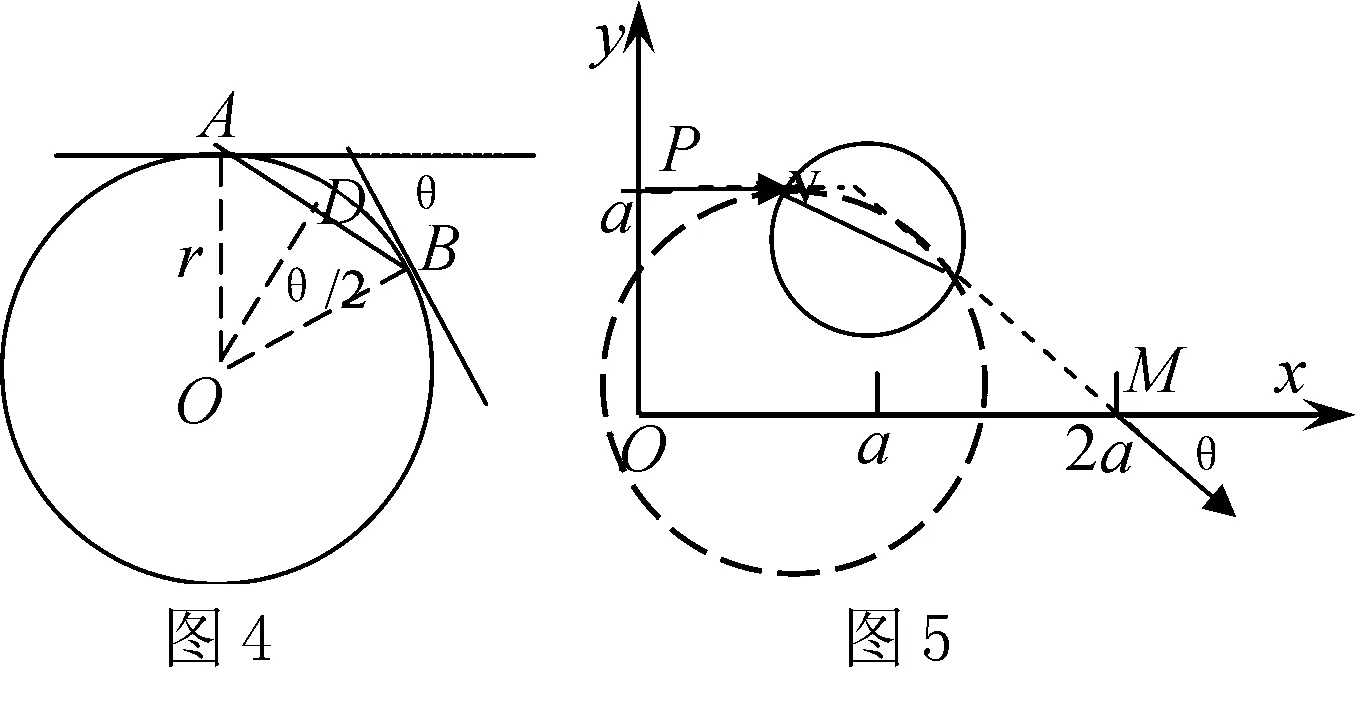
标中与两速度矢量相切(如图5所示),过两切点作轨迹圆的弦,则最小圆形磁场的区域的圆直径就是此弦的长度.弦的长度AB可根据几何关系求得,如图4所示,过两速度的矢量与圆轨迹的切点A、B各作两条垂线AO、BO相交于O点,则∠AOB=θ= 60°,过O作弦AB的垂线OD,则∠DOB=θ/2=30°, ∴弦AB=2rsin30°=r,故能达到此目的的最小圆形磁场区域的半径R=r/2=mv/2qB.
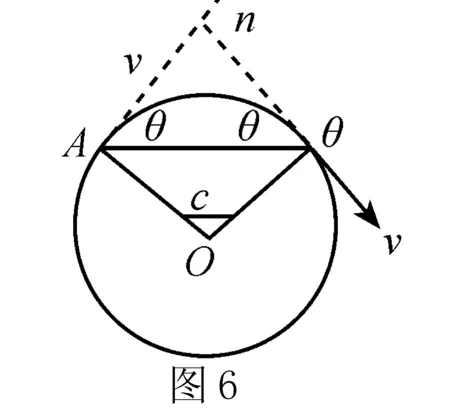
策略四 利用粒子速度的偏向角 等于粒子转过的圆心角找α,偏向角就是指粒子在某一时刻的速度与原来速度之间转过的角度,如图6所示,速度的偏向角φ等于AB所对的圆心角α,并与时间成正比,即φ=α=ωt.
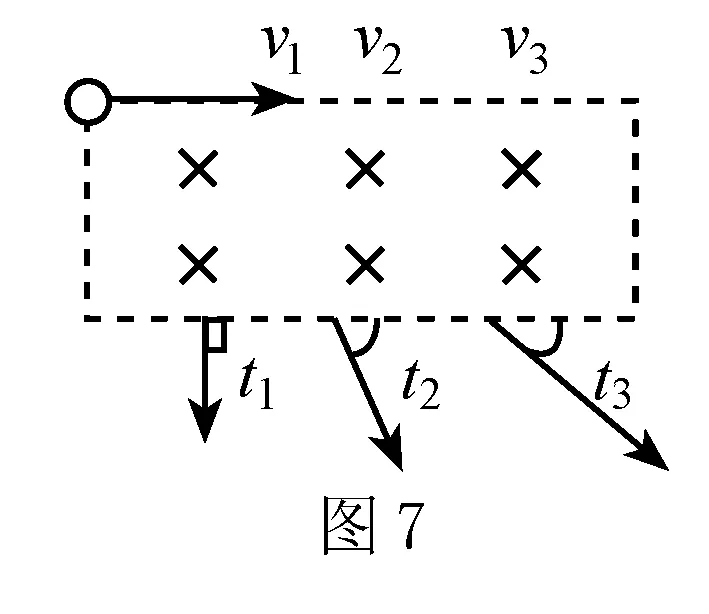
例3 如图4所示,三个同样的带电粒子,分别以速度v1,v2,v3沿水平方向从同一匀强磁场中,离开磁场时它们与水平边界线的夹角依次为α1=90°,α2=60°,α3=30°.若依次以t1,t2和t3表示每个粒子在磁场中的运动时间,下列哪些说法正确?
A.t1最长,t3最短 B.t1最短,t3最长
C.t1=t2=t3D.t1=t2t3
策略五、充分利用圆的对称性, 圆有多种对称性,解题时若能充分利用对称性,可以加速解题的进程.
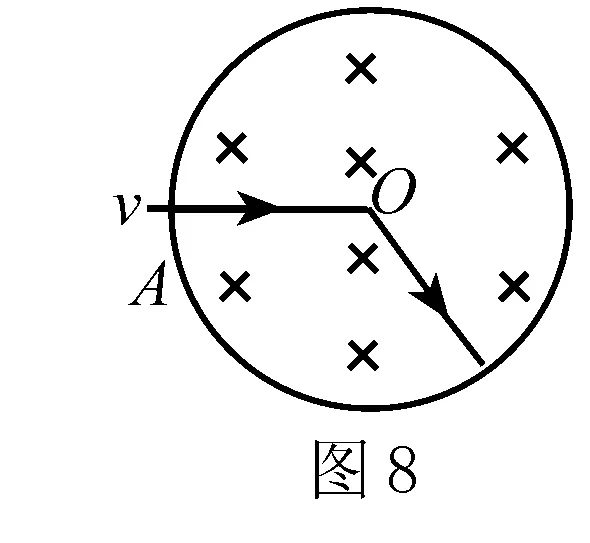
例4 如图8所示,在内部半径为r的绝缘细筒中,有平行于圆筒轴线方向的匀强磁场,筒内为真空环境,一个质量为m,电量为+q的粒子,自筒壁A处的小孔以速度v沿筒半径方向垂直于磁场射入筒中,粒子在筒内空间运动时只受洛伦兹力作用,而且粒子在与筒壁碰撞时无机械能损失,并保持原有电量,如果粒子在筒内与筒壁相继碰撞若干次运行一周后恰好仍从A孔射出,筒内磁感应强度B必须满足什么条件?所需时间t是多少?

策略六、从特殊到一般画出动态圆,探索极值

例5 带电粒子在垂直于磁场方向的平面上受洛伦兹力做圆周运动,而粒子以不同速度射入磁场,每一粒子都在不同的圆轨迹上运动,此类问题先确定动态圆的圆心轨迹,考虑电子在磁场中的约束条件,作出动态圆进行探索,容易发现临界状态,从而找到极值.
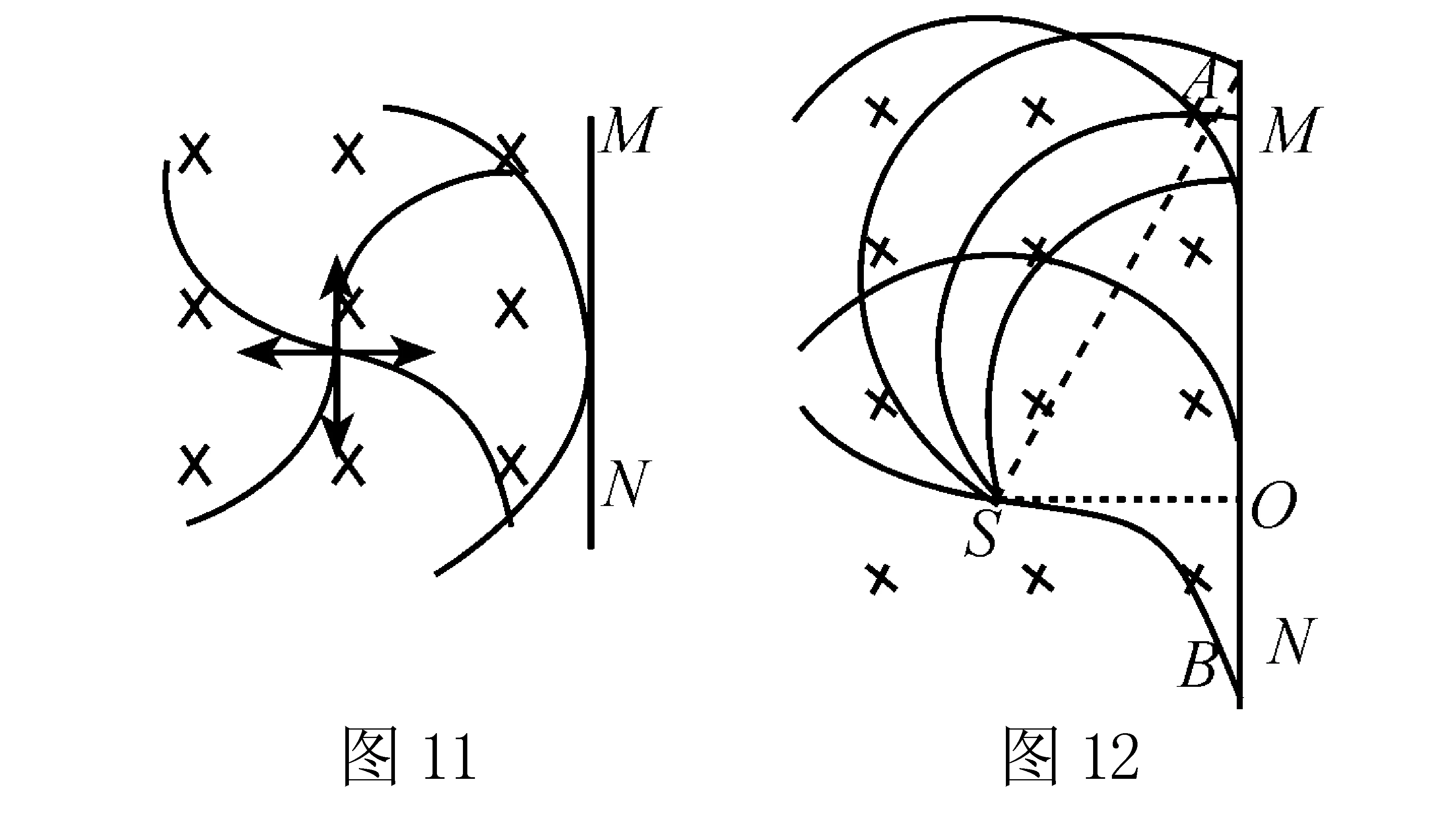
例5S为电子源,它只能在图10中所示纸面上360°范围内发射速率相同,质量为m,电量为e的电子,MN是一块足够大的竖直挡板,与S的水平距离OS=L,挡板左侧有垂直纸面向里的匀强磁场,磁感应强度为B,求:
(1)要使S发射的电子能够到达挡板,则发射电子的速度至少多大?
(2)若电子发射的速度为eBL/m,则挡板被击中的范围多大?
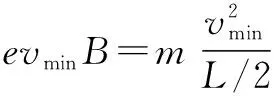
G632
B
1008-0333(2016)28-0069-02
