“等差数列前n项和”两道例题的教学的思考

何金栋●

宁夏固原市隆德县职业中学 (756300)



“等差数列前n项和”两道例题的教学的思考

何金栋●

宁夏固原市隆德县职业中学 (756300)

在数学教学过程中，例题的教学不只是简单讨论解法，教会学生解题方法，而是要更深层次地挖掘例题所蕴含的思想和方法，让学生掌握一种研究知识模块的思路和一般性的方法.

例题教学；例题蕴含的数学思想方法；研究方法

人教A版必修5第二章《数列》中“等差数列的前n项和”一节例3与例4的教学，由于既涉及到刚刚学习了的等差数列的基础知识，又用到前面学习的关于一般数列的重要结论.所以，我认为在教学中要引起教师的足够重视，通过教师设置相关教学问题，引导学生发现例题中所蕴含的数学思想与解题方法，并且能够形成研究数列问题的一般性的流程，为后面等比数列的学习打下良好的基础和提供探索研究的思路.先说说例3的教学.

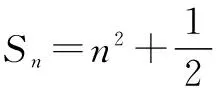
第一，一般数列的通项与前n项和的关系的准确认识.对于一个数列{an}，它的前n项和Sn的意义是，Sn=a1+a2+…+an-1+an，Sn-1=a1+a2+…+an-1，n=1时，a1=S1，当n≥2时，an=Sn-Sn-1.

第二，这里本身就用到了一个结论:等差数列的通项公式是关于n的一次函数或常数函数，其中p、q是常数.这也是在学习等差数列的通项公式时讨论得出的结论，而不必通过它的通项公式再用定义证明.

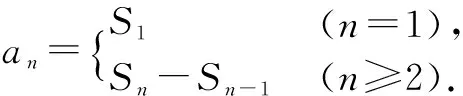
第四，完成课本例3后面的探究：一般的，如果一个数列{an}的前n项和为Sn=pn2+qn+r，其中p、q、r都是常数，且p≠0，那么这个数列一定是等差数列吗？如果是，它的首项和公差分别是什么？

教师要引导学生通过等差数列的前n项和公式：

再说说例4的教学 .

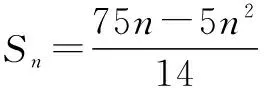
可以看出，例3与例4的学习也是一脉相承的.就是对等差数列的前n项和当公差d≠0时是关于n的二次函数的再认识.同时再次强调了研究数列把它看成是关于n的函数，从函数角度来解决数列问题的方法.

要设置以下类似的相关问题，引导学生进行更深入的研究.①既然数列是函数，数列的通项是函数，数列的前n项和也是函数，那么我们就可以用研究函数的方法去研究数列、数列的通项和数列的前n项和以及与之相关的问题.

②作为函数的数列一定有最大值和最小值 吗？

③等差数列在什么条件下会有最大或最小值？

④除了利用二次函数求等差数列前n项和的最值，还有别的什么方法？

通过以上问题的讨论，可得出以下重要结论：

一、等差数列{an}当a1>0,d<0时，数列为递减数列，前n项和Sn有最大值；当a1<0,d>0时，数列为递增数列，前n项和Sn有最小值.

二、通过通项公式来求等差数列的前n项和的最值的方法：

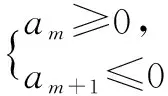
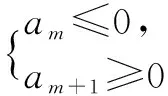
经历以上相关问题的设置与讨论，相信同学们会对等差数列有一个更深的认识，对等差数列的相关知识有一个更全面的掌握，同时对后面将要学习的等比数列，提供了很好的研究思路和方法，为等比数列的学习打下了良好的基础和积累了丰富的经验.也为整个数列模块的学习形成了一个一般性的研究方案.

G632

B

1008-0333(2016)28-0050-01