浅谈变式教学在唤醒数学课堂活力中的作用

唐 鹏●

江苏省外国语学校 (215104)



浅谈变式教学在唤醒数学课堂活力中的作用

唐 鹏●

江苏省外国语学校 (215104)

数学课堂需要活力，不少教师的课堂比较乏味，大量充斥着教师“一讲到底”、 “机械式问答教学”，变式教学可以唤醒数学课堂的活力，给我们的数学教学带来一股春风.

活力;高中数学;课堂教学;变式教学

随着课改的发展，高中数学课堂活动也不断发生着变化.过去的“灌输式”教学往往一片死气沉沉,而热闹的“合作探究”背后往往是虚假的繁荣，学生要么被动地听,要么不动脑筋地做，整个课堂缺乏真正思维的活力.不少教师也在苦恼，为何教了好多遍、强调了好多次的知识点总是错,而刚刚讲了、练了的题型，为何很快就忘了？

课堂教学的魅力不在于形式的多样化，而在于充分激发学生的兴趣，唤醒课堂活力，从而让学生高效扎实掌握知识点并能灵活运用.因而如何让学生真正成为课堂的主体才是唤醒数学课堂活力的根本方向.笔者看来，“变式教学”是一种行之有效的教学手段.

“变式教学”是指在课堂教学中，遵循一定的原则，灵活的使用对命题的合理转化的一种教学模式.教学方式灵活多变，学生适应和接受快，在唤醒数学课堂活力中有其突出的地位和作用.

一、变式教学有助于学生感受到数学美，有利于唤醒课堂教学的活力

在数学课堂中，就一道题讲一道题往往是机械枯燥的，学生兴趣不大，感受不到数学的美、思维的快乐，效率自然低下.恩格斯说，“思维着的精神是地球上最美的花朵”，在变式教学中，教师不仅传授知识，同时也能让学生在数学学习中感受美、追求美，促进他们主动思考，充分发挥其主观能动性，使数学课堂焕发出新的活力.

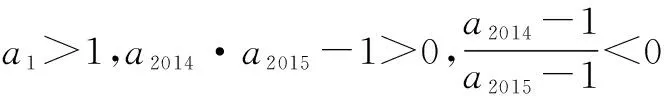
变式 设等差数列{bn}的公差为d，其前n项和为Sn，首项b1>0，b5+b6>0，b5·b6<0，则使Sn>0成立的最大自然数n=____.

案例1的难度较大，即便通过教师讲解，也是一知半解，知其然不知其所以然，通过设计变式，巧妙利用了等比数列第一项与最后一项的乘积和第二项与倒数第二项的乘积相等，等差数列第一项与最后一项的和与第二项与倒数第二项的和相等这一类似的性质，让学生在已经解决案例1的前提下，轻松解决变式，把复杂问题变得简单，同时在类比的过程中，深刻感悟到等差、等比数列的本质规律，轻松解题，从中体会到数学的美.每一次这样的发现，都让学生产生一种发自内心的愉悦，体现出数学的无穷魅力.苏霍姆林斯基说：“教给学生能借助已有知识去获得知识，这是最高的教学技巧之所在”.通过变式，找到知识与知识的内在联系，体会到“柳暗花明又一村”的欣喜，这就是数学美的具体体现.变式教学让学生想要去发现，想要去了解，变被动为主动，从而唤醒数学课堂新的活力.

二、变式教学有助于学生自主探究，合作交流，从而唤醒数学课堂的活力

教育心理学家指出，我们教学生怎样思考，怎样创造性的思考，我们教学生怎样解决问题，怎样创造性的解决问题.很多教师的课堂只能听到老师的声音，不能把学生的注意力吸引到对数学问题的探究上，或者有些教师的课堂很“热闹”，但是学生的活动是空洞的，无效的.有活力的数学课堂不仅在于教师讲的精彩，更加在于学生学的主动；有活力的课堂，只有让学生不断的提出自己的问题，自主的解决问题.因此，通过变式教学，我们可以让学生在原来的问题中产生新的碰撞，让学生变成问题的主人，引导学生产生有价值的变式，在合作探究中获得比以往更多的收获.只有这样，才能充分唤醒学生的问题意识，从而唤醒数学课堂的活力.

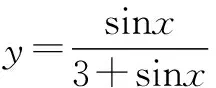
笔者进行了这样的设计，

师：你还能找到哪些类似的函数求值域？大家可以分成小组一起探讨，并找到求这些函数值域的方法，我们再来一起交流.

通过学生的自己努力，他们找到了很多有价值的变式，比如改变分子分母的结构特点，分母次数高于分子的，或者改变函数定义域，从而发现利用基本不等式求最值时，当“=”不能取到时等等……

在数学课堂中，通过变式教学让学生发现问题与问题之间的联系与区别，才能让学生体会到数学是活动的、动态的、开放的，才会更易于理解与接受，在开放的变式教学中让学生说说各自的问题和解决的方法，尽情地发挥自己独特的思维与想象.通过自主探究，合作交流，教师大胆鼓励，让学生在实验中发现、讨论，让学生感到自己是一个发现者、研究者、探索者，是问题的主人，唤醒学生的求知欲，进而唤醒数学课堂的活力.

三、变式教学通过问题串，打开学生思维的大门，唤醒数学课堂的活力

数学课堂重在思维，要提高数学课堂的效率，就必须给学生创设一个充满活力的课堂，变式教学让数学课堂中注入了这样一种活力，不断激发学生的学习热情，唤醒他们的思维活力，让课堂再往前一点，课后留给学生的感悟再多一点.笔者在教授“直线和圆”这一章节时，有这样一个例子：

案例3 已知m为实数，直线l1:mx+y+3=0,l2:(3m-2)x+my+2=0，则“m=1”是“l1∥l2”的____条件.(在“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”中选择一个合适的填空)

为此，设计了以下变式：

变式(1) 已知m为实数，直线l1:mx+2y+1=0，l2:3x+(m+1)y-1=0，则“m=2”是“l1∥l2”的____条件.(在“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”中选择一个合适的填空)

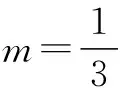
在上述问题中，把学生的易错点，通过变式不断地展现在学生面前，让学生去分析，去思辨，从而加深对数学基础知识的掌握，激起学生强烈的求知欲.学生在解决了案例3时，自我感觉良好，答案也是对的，似乎没什么需要反思和注意的了，结果通过变式1，发现原来没有考虑直线重合这一特殊情况，等教师讲解了，感觉又没有问题了，教师再抛出变式2，学生做完发现自己又出现问题了，忽略了斜率不存在的情况.这时候学生就会去反思，自己做题出现漏洞的原因是什么，在解决直线平行与垂直问题中应注意些什么.通过一题多变，拓宽学生思维的深度与宽度，开阔学生的视野，使学生感受到思考问题，应用数学的乐趣，激发数学课堂的活力.

在高中数学课堂中，我们需要去思考怎样运用教材，合理设置教学步骤，怎样将有利于唤醒课堂的活力并有利于学生创造思维的培养.同时还要注意，课堂有时候的活跃不等于学生思维活跃，是否存在为活动而活动的倾向，是否所有学生或者大部分学生都参与到我们的教学过程中来了.教师必须灵活运用各种教学手段，比如变式教学，根据学生现有的知识水平，引导学生积极有效的思维，保持数学课堂的活力.设法由学生自己提出变式，然后再将学生的思考引向深入.最后要反思，我们是否从根本上解决了学生存在的问题，我们讲解的是否是学生真正希望了解的.德国教育学家第斯多惠：教学的艺术不在于传授的本领，而在于激励、唤醒、鼓舞.数学课堂不应是一成不变的，教师通过灵活运用变式教学等教学方法，通过多种方式促进学生思维的发展，才能真正唤醒数学课堂的活力，真正将学生作为课堂的主体.

[1]郑毓信.数学教育的现代发展[M]. 南京：江苏教育出版社，1999.

[2]曹才翰,章建跃.数学教育心理学[M].北京：北京师范大学出版社，1999.

[3]吴小峰.数学变式教学的作用与意义[J].数学教学.2009(6)

[4]王淼生.数学美本质上终究是简单[J]. 数学教学,2013(03)

G632

B

1008-0333(2016)28-0046-02