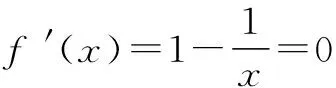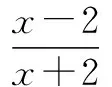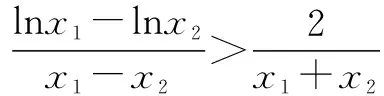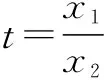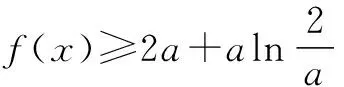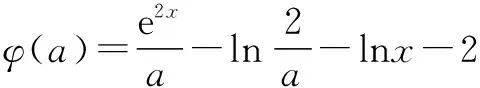利用导数证明不等式的常见题型与解法研究

江 浩●

江苏省沭阳如东中学(223600)



利用导数证明不等式的常见题型与解法研究

江 浩●

江苏省沭阳如东中学(223600)

题型一 证明f(x)

例1 (2016年全国卷Ⅱ第21题改编)证明：当x>0时，(x-2)ex>-x-2.

证明 令f(x)=(x-2)ex+x+2，则f′(x)=(x-1)ex+1.记φ(x)=f′(x)，则φ′(x)=xex>0，即f′(x)在(0,+∞)上递增，所以f′(x)>f′(0)=0，可见f(x)在(0,+∞)上递增，所以f(x)=(x-2)ex+x+2>f(0)=0，故原不等式得证.

题型二 证明ψ(x1,x2)>α

例3 (2016年全国卷Ⅰ第21题)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.

(Ⅰ)求a的取值范围；(答案：a>0)

(Ⅱ)设x1,x2是f(x)的两个零点，证明：x1+x2<2.

证明 通过对(Ⅰ)的求解，可知当a>0时，f(x)在(-∞,1)上单调递减，在(1,+∞)上单调递增.不妨设x1f(2-x2)，只要证明f(2-x2)<0.由于f(2-x2)=-x2e2-x2+a(x2-1)2，f(x2)=(x2-2)ex2+a(x2-1)2=0，所以f(2-x2)=-x2e2-x2-(x2-2)ex2.设g(x)=-xe2-x-(x-2)ex，则g′(x)=(x-1)(e2-x-ex).当x>1时，g′(x)<0，而g(1)=0，故当x>1时，g(x)<0，故x1+x2<2得证.

例4 (2014年南京三模)已知函数f(x)=lnx-mx有两个不同的零点x1,x2，求证：x1x2>e2.

证明 不妨设x1>x2>0，则f(x1)=lnx1-mx1=0，f(x2)=lnx2-mx2=0.

题型三 证明φ(x,α)>α

对于证明φ(x,α)>α类型问题，可以采用更换主元的方法使问题变得简单易解.此类问题还有如：已知1≤ylnx-lny，也可以采用这种方法求解；当然也可以先利用导数求f(x)=φ(x,α)的最小值，然后进行适当放缩达到目的.

G632

B

1008-0333(2016)28-0034-01