一道黑龙江省考题的解法研究

苏保明●

云南省蒙自市蒙自一中(新校区)(661100)



一道黑龙江省考题的解法研究

苏保明●

云南省蒙自市蒙自一中(新校区)(661100)

在平时的解题中常常会遇到一类带条件的整式型最值问题，而这类问题解决难度不大，只要认真思考、仔细研究，就一定能找到最佳解法. 本文列举一例解析如下：

(Ⅰ)求实数m的取值范围；

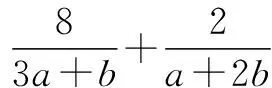
解 (Ⅰ)因为函数f(x)的定义域为R，所以|x+2|+|6-x|-m≥0在R上恒成立，所以|x+2|+|6-x|≥m在R上恒成立，设g(x)=|x+2|+|6-x|，则g(x)min≥m．

因为|x+2|+|6-x|≥|(x+2)+(6-x)|=8，所以g(x)min=8,所以m≤8．

针对第(Ⅱ)问，经过笔者认真思考和研究，给出下面多种解法.

方法一 常数代入法

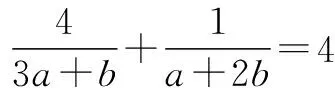
解法1 (Ⅱ)由(Ⅰ)知m≤8，所以n=8，

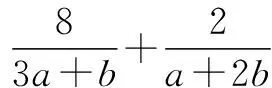
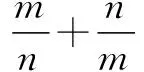
方法二 利用公式求最值.

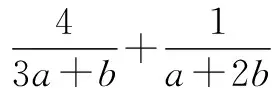
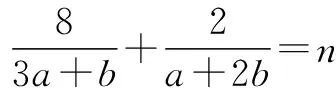
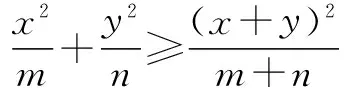
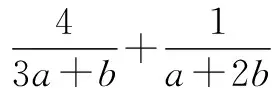
方法三 三角法

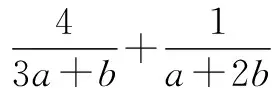
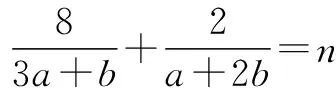
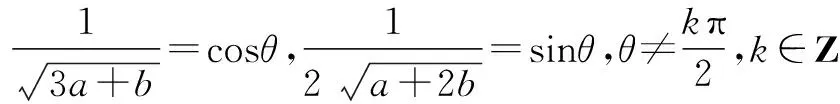
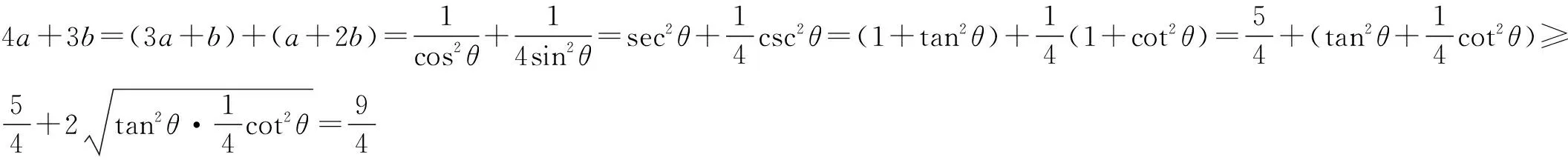
评注 遇到二元二次代数式(或等式),若能化为两个非负数的和为1时,则可利用cos2α+sin2α=1设出适当的三角代换式，即把所求问题转化为三角问题进行求解.

方法四 向量法

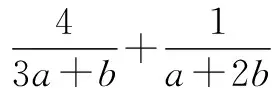
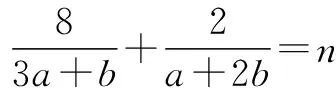
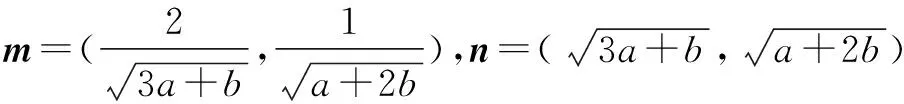
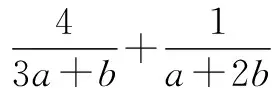
方法五 柯西不等式法

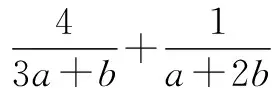
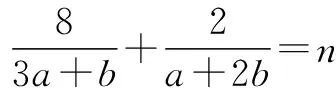
评注 柯西不等式的引入，为解决某些相关的数学问题添增了新的思想方法，并能给解题者一种快乐感和成功感.本题通过柯西不等式把较为复杂的问题转化为简单的代数不等式问题，从而快速、准确解决.

方法六 “零值”法

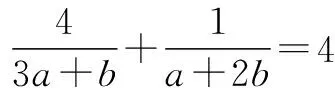
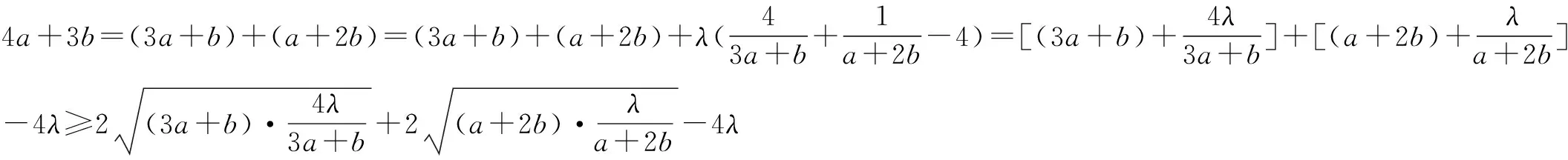
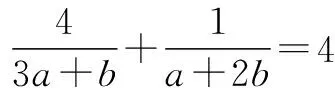
评注 有时求整式(或分式)的最值问题时，可通过构造“零值”型等式，从而转化为含参数λ的不等式，其中需要根据等号成立的条件先求出参数λ的值，进而求出原问题的最值.

G632

B

1008-0333(2016)28-0013-02