圆锥曲线的一组性质探究

杨建益● 吴宝树●

福建省泉州市第七中学(362000)



圆锥曲线的一组性质探究

杨建益● 吴宝树●

福建省泉州市第七中学(362000)

椭圆、双曲线、抛物线源出一族，其性质具有许多相似之处．笔者通过探究，得到圆锥曲线的一个新的共同性质．

将椭圆的性质横向推广到双曲线和抛物线上，还可以得到如下两个性质：

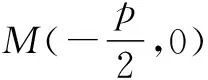
性质2,3证明同性质1，过程略.

分析性质1的推导过程，我们不难发现，直线所过的 轴上的定点具有一般性，进一步推导而可以得到一组更一般的性质.

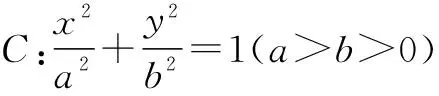
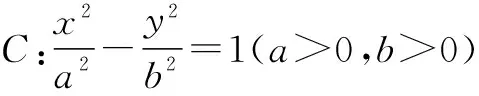
性质6 过x轴上的定点(n,0)(n>0)且不与y轴垂直的直线交抛物线C:y2=2px(p>0)于P,Q两点，则在x轴上存在点M(-n,0)，使得MF平分∠PMQ.

从圆锥曲线的上述性质出发，笔者尝试命制一些有趣的试题，既考查了学生的运算求解能力，又能考查学生对圆锥曲线定义的掌握情况，现展示如下.

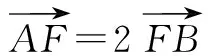
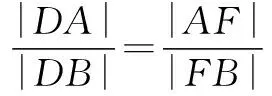
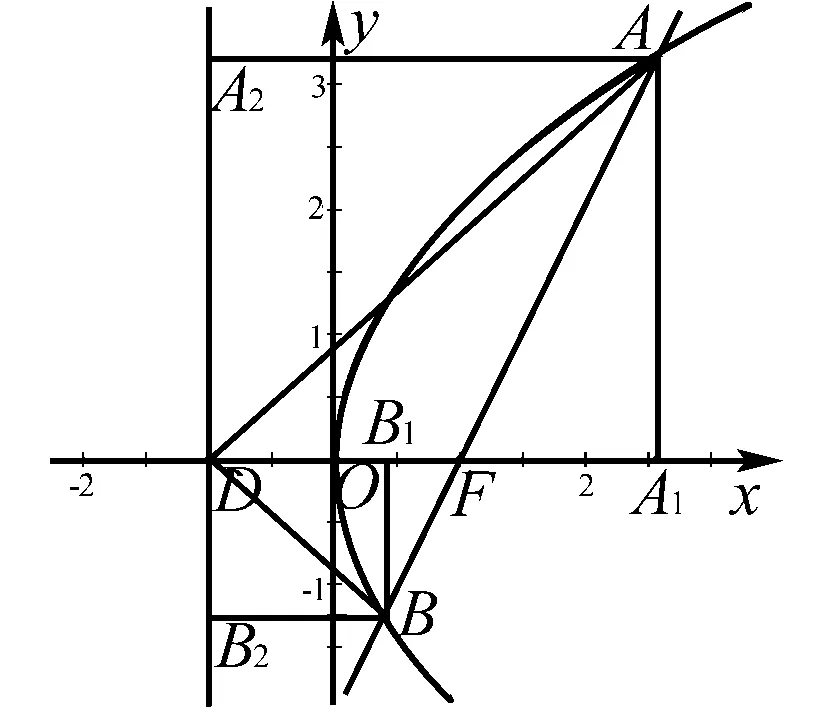
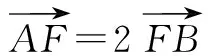
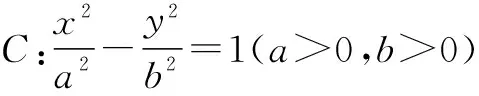
(Ⅰ)求椭圆C方程；

(Ⅱ)若点D(2,0)，连接直线DA，DB,记直线DA的斜率为k1，直线DB的斜率为k2，试探究k1+k2是否为定值.

限于篇幅，本题解析略.

G632

B

1008-0333(2016)28-0015-01