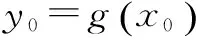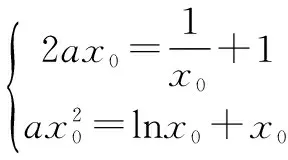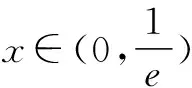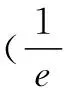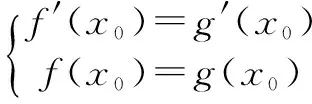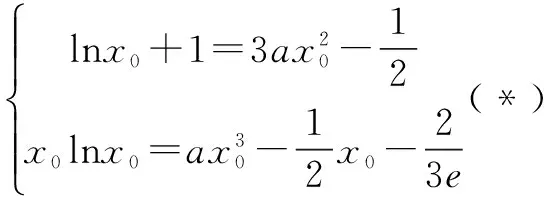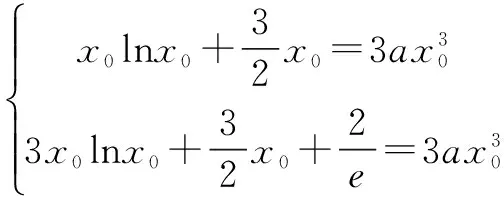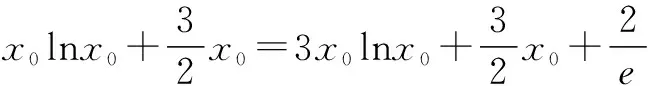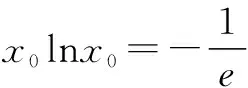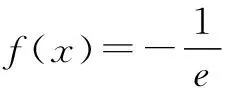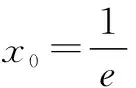例谈两类“相切”问题的求解
2016-12-16童永奇
童永奇●
陕西省西安市临潼区马额中学(710609)
例谈两类“相切”问题的求解
童永奇●
陕西省西安市临潼区马额中学(710609)
本文拟通过归类举例的形式,着重说明:借助导数的几何意义,可以顺利探求与曲线“相切”的一些常考的数学问题.
类型一、直线与曲线“相切”问题
解题理论1 曲线y=f(x)在点(x0,f(x0))处的切线方程为y-f(x0)=f'(x0)·(x-x0).
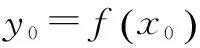
1.根据直线与曲线相切,求参数的值
例1 (2016年高考数学全国Ⅱ卷理科第16题)若直线y=kx+b是曲线y=lnx+2的切线,也是曲线y=ln(x+1)的切线,则b=____________.
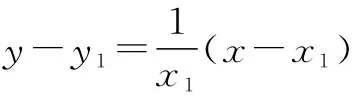
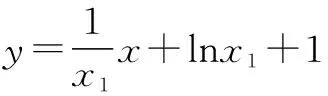
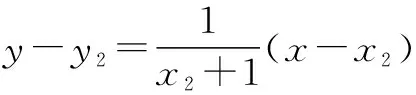

于是,由①②得
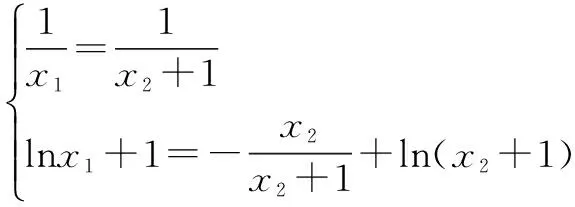
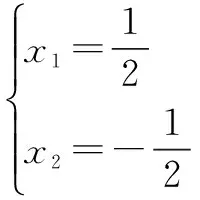
故b=lnx1+1=1-ln2.
(方法二)设直线y=kx+b与曲线y=lnx+2相切于点(x1,y1),则

设直线y=kx+b与曲线y=ln(x+1)相切于点(x2,y2),则
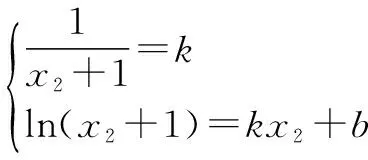
于是,根据③④可得b-1=1-k+b,化简得k=2,将之代入①即得b=1-ln2.
评注 一般地,遇到直线与曲线相切,往往需要设出切点的坐标,或根据切线方程来解决(如方法一),或根据题意列方程组加以灵活处理(如方法二).
2.根据直线与曲线相切,巧求含参函数的零点个数
例2 已知a>1,试讨论函数f(x)=ax-x(a>1)的零点个数.
解析 先分析直线y=x与曲线y=ax(a>1)相切时,参数a的取值.
因为切点在直线y=x上,所以可设切点坐标为(x0,x0).
由y=ax求导得y′=axlna,所以根据切线方程为y=x即得ax0lna=1. (*)
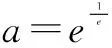
接下来,再结合图形分析.

评注 上述求解的关键是先分析临界情形,再灵活运用指数函数的图像规律加以思考.
3.根据直线与曲线相切,巧求参数的取值范围
例3 (2016年西安八校联考(三)理科第12题)函数f(x)=lnx-ax2+x有两个零点,则实数a的取值范围是( )

当x>e时,t′(x)<0.所以函数t(x)在(0,e)上递增,在(e,+)上递减.
又易知:当x→0时,t(x)→-;当x→+时,t(x)→1.
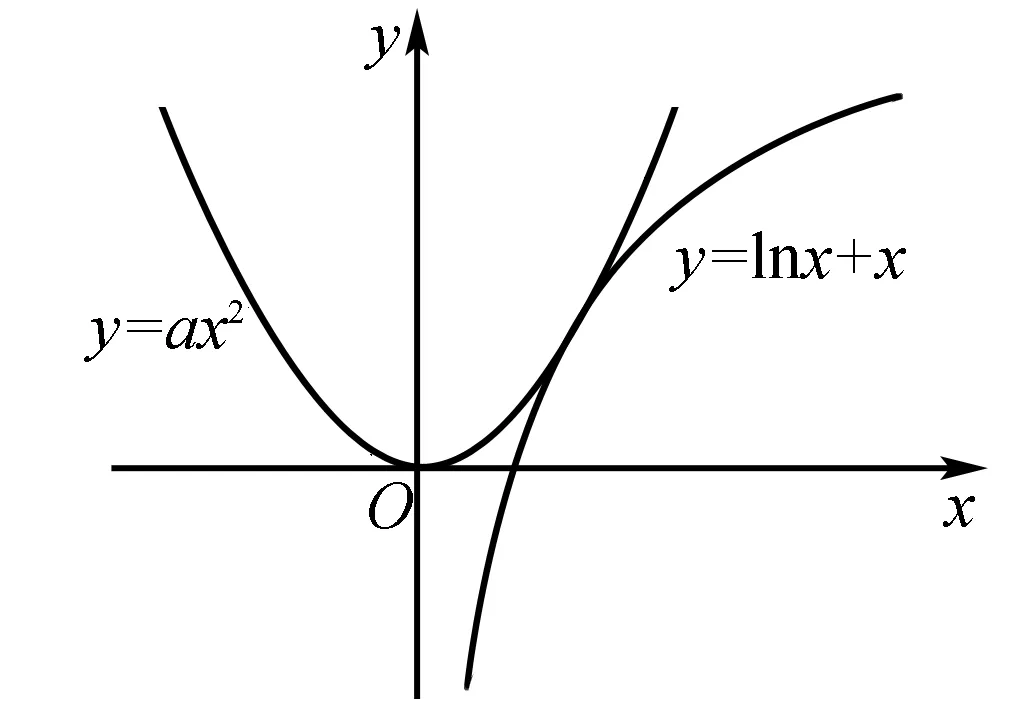
据此可画出函数t(x)的图像(如图1),让直线y=ax绕着坐标原点旋转分析即知:为满足题意,需要0 图1 接下来,具体分析直线与曲线相切情形. 令s(x)=2lnx+x-1,则因为易知函数s(x)在t(x)在(0,+)上递增,且s(1)=0,所以方程2lnx+x-1=0有唯一实数根x=1.从而,可知x0=1,所以kOP=t′(1)=1. 综上,由(**)知所求0 1.根据曲线与曲线相切,巧求函数的取值范围 例4 【同例3】(2016年西安八校联考(三)理科第12题)函数f(x)=lnx-ax2+x有两个零点,则实数a的取值范围是( ) 解析 由题设得方程f(x)=0,即ax2=lnx+x有两个不相等的实数根.于是,原问题可化归为当曲线y=ax2与y=lnx+x有两个交点时,求实数a的取值范围.先分析曲线y=ax2与y=lnx+x相切时,参数a的取值. 图2 令s(x)=2lnx+x-1,则因为易知函数s(x)在t(x)在(0,+)上递增,且s(1)=0,所以方程2lnx+x-1=0有唯一实数根x=1.从而,可知x0=1,进而可得a=1. 接下来,再结合图形分析. 根据二次函数的图像规律“二次项系数的绝对值越大,则开口越小”,可知:为满足题意,需要0 评注 上述求解的关键是先分析临界情形,再灵活运用二次函数的图像规律加以思考. 2.根据曲线与曲线相切,巧求参数的值 (Ⅰ)求函数f(x)的单调递增区间和最小值; (Ⅱ)若函数y=f(x)与函数y=g(x)的图像在交点处存在公共切线,求实数a的值. 评注 本题第一问比较简单,难点在于第二问,如何求解方程组(*)——这里采取的方法是:先消去实数a,借助(Ⅰ)的解析过程得到x0的值,再根据其中的一个方程求a的值. 综上,多关注直线与曲线“相切”,或曲线与曲线“相切”在解题中的灵活运用,可帮助我们巧妙分析、解决一些相关的数学问题,从而不断积累解题经验,逐步提升解题技能. G632 B 1008-0333(2016)28-0004-02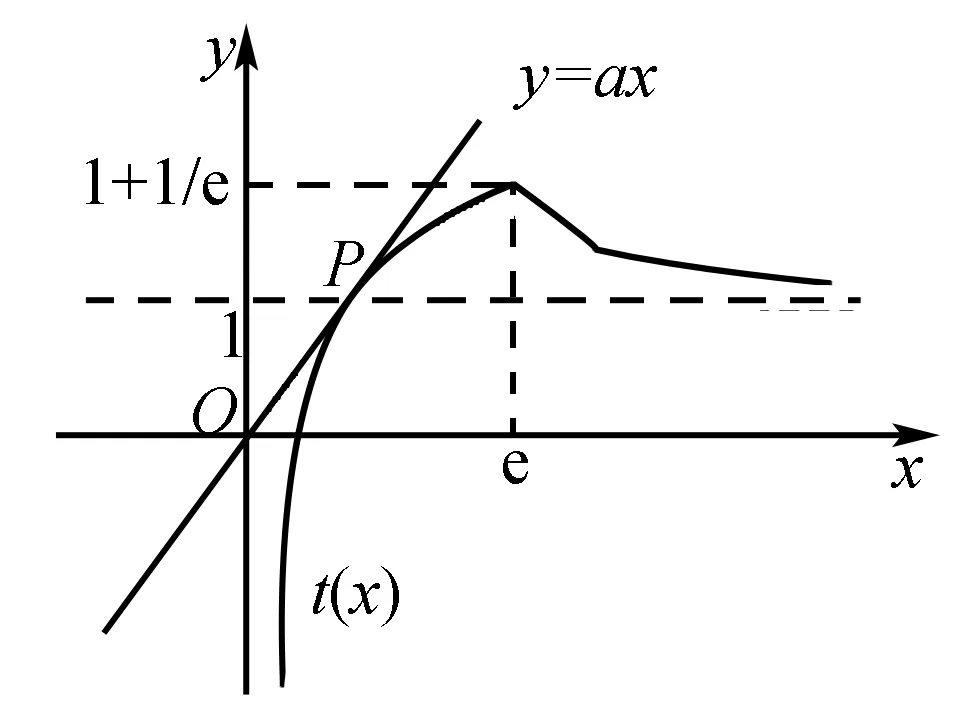
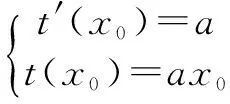
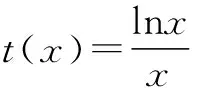
类型二、曲线与曲线“相切”问题