计重收费模式下运营车辆荷载的POT模型
2016-12-16赵高鹏黄海云张俊平袁伟璋
赵高鹏,黄海云,张俊平,2,袁伟璋
(1.广州大学,广东 广州 510006;2.广东交通职业技术学院,广东 广州 510650)
计重收费模式下运营车辆荷载的POT模型
赵高鹏1,黄海云1,张俊平1,2,袁伟璋1
(1.广州大学,广东 广州 510006;2.广东交通职业技术学院,广东广州 510650)
当前我国高速公路车辆超载超限运营现象尤为严重,研究在计重收费模式下运营车辆荷载的极值以及其发展变化趋势成为十分迫切的问题。基于计重收费模式下广东省某高速公路的动态称重数据,对车辆荷载按车型进行了车辆总重的统计分析,采用极值分析理论建立POT模型,得出车辆总重分布的尾部分布函数,并科学地预测出未来任意重现期内可能出现的车辆荷载极值。结果表明,该高速路段出现超大吨位车辆并非偶然,在未来还可能出现更大吨位的车辆荷载,对既有道路桥梁的安全运营构成了严重的威胁。可为有效控制运营车辆超载提供参考。
车辆荷载;计重收费;极值理论;POT模型
0 引 言
随着我国经济与社会及汽车工业的不断发展,超载超限运输不断加剧,公路运营车辆荷载产生了显著的变异,成为新兴研究热点课题之一。为了有效地遏制日趋严重的超载现状,更好的保障交通安全畅通,计重收费的管理模式应运而生。车辆计重一般多采取动态称重技术(WeightInMotion,简称WIM),已在我国多条高速公路上成功应用。在计重收费模式下,超载超重车辆是否得到有效控制?运营车辆荷载的特征有何变化?如按现行计重收费政策,运营车辆荷载的发展变化趋势是什么?如何才能做到较为科学合理地预测、并以此来改进计重收费政策?等等。围绕这些问题,一些研究者进行了探索分析[1~6],但总的说来,这些研究尚属初步,得出的结论也大相径庭,加之运营车辆荷载特征本身也存在比较明显的地域性,导致问题更为复杂。鉴于此,本文以京珠高速广韶段某收费站的实测数据为基础,运用极值分析理论[7]构建了运营车辆荷载模型,对计重收费模式下运营车辆荷载的现状、发展趋势进行较为系统全面地探讨。
1 车辆荷载统计分析
京珠高速是一条首都放射性高速公路,连接北京和广州、珠海、香港等南部城市,为我国南北交通的大动脉,在珠三角路网中起骨架作用。广东省于2009年11月1日起对境内的京珠高速开始实行高速公路货车计重收费政策,本文随机选取了其中具有代表性的某计重收费站2014年4月为期30d 的80181个车辆荷载数据进行研究分析。
实测的车流量数据的整理按照《广东省高速公路收费车辆车型分类标准》划分为五类,在五类车型中:
一型车最多,占总车流量的49.3%,主要有小轿车、吉普车、的士头货车、摩托车等,共测得39533辆车,平均总重1.8t,分布范围较为集中,数据的离散型小。
其次是五型车,总车流量的32.4%,主要包括重型货车、重型拖(挂)车、40in集装箱车等车辆,共采集到25952辆车,平均车重48.8t。其总重分布范围最大,车重分布从10~110t,有两个峰值,分别在20t和55t附近,最大车重107.9t。
再次是三型车,占总车流量的13.5%,三型车以中型客车、大型客车、中型货车为主,共测得10826辆车,平均车重11.2t。其总重分布范围比较分散,总重分布出现两个峰值,分别在3.5t和14.5t附近。
最少的是二型车和四型车,分别占车流总量的2.0%和2.8%[8]。
整理结果可知,一型车数量较多,但以小轿车为主,车辆荷载相对较小;三至五型车则以重车为主,是本文需要研究的重点。三型车、五型车总重频数直方图见图1、图2。
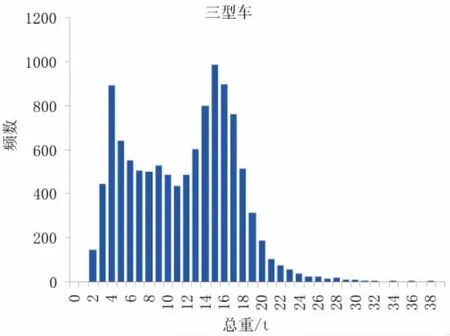
图1 三型车总重频数直方图
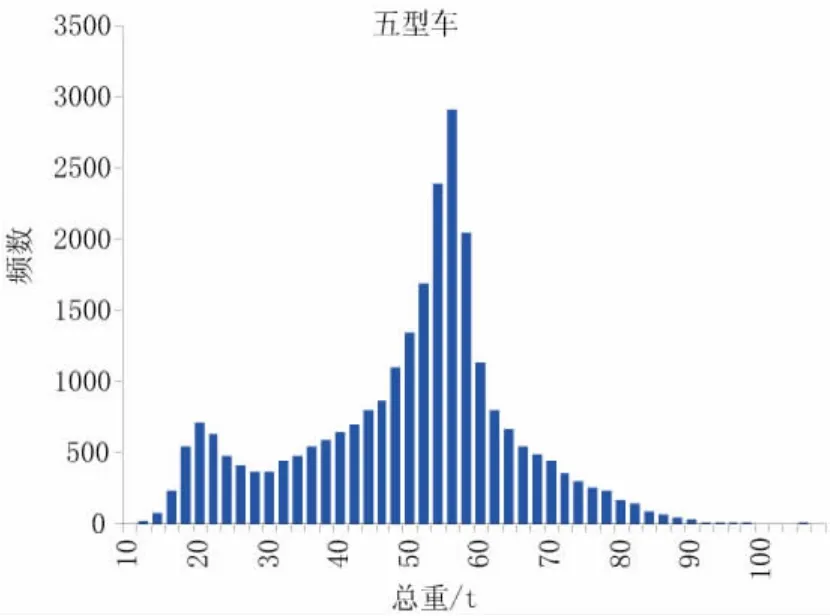
图2 五型车总重频数直方图
2 基于极值分析理论的POT模型
目前,国内外大多数研究者在构建运营车辆荷载模型时,通常采用假设检验、分析参数的技术路线[2,7,8]。这种试错的分析方法具有较强的主观性,即使能通过K-S、x2、U2等检验,也只能较好地模拟分布的中部,却未能恰当地、准确地描述运营车辆荷载分布的尾部,而分布的右尾部亦即运营车辆荷载的极值才是构建运营车辆荷载模型的关键和核心。基于此,本文拟采用极值分析理论来构建运营车辆荷载模型。
2.1POT模型[10]
假设独立同分布随机变量序列{Xi}的任意分布函数为F(x),F(x)支撑的上端点x*,存在某个值Xi<μ<x*,称μ为阈值(Threshold),Xi为随机变量序列,(Xi-μ)为超出量序列。定义Fμ(y)为随机变量超过阈值μ的条件分布函数,则可表示为:
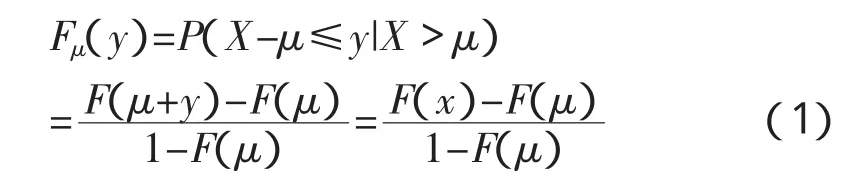
则

设X1,X2,…,Xn是来自同分布F(x)总体的一个样本,如果随机变量X的分布函数能满足:
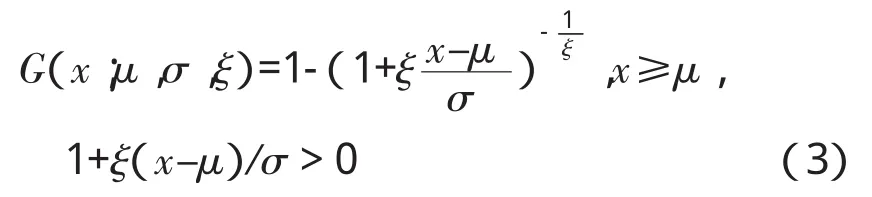
则称X服从广义帕累托分布(GeneralPareto Distribution,简称GPD分布)。其中μ∈R是位置函数,σ>0是尺度参数,ξ∈R是形状参数。
若存在常数an和bn,使得当趋近F(x)的上端点时,Fμ(an+bn)有连续的极限分布,则极限分布定理成立。
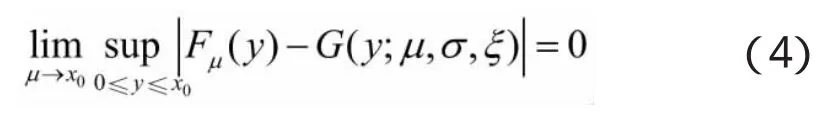
该定理说明:对于充分大的阈值μ,多数未知分布函数F(x)的超出量分布函数Fμ(y)可用GPD分布G(y;μ,σ,ξ)近似,即为Fμ(y)≈G(y;μ,σ,ξ),将该式代入式(2)可得:
F(x)=G(y;μ,σ,ξ)(1-F(μ))+F(μ) (5)
当μ确定以后,可以得到{Xi}中比阈值μ大的个数Nμ,根据式(5)用频率(1-Nμ/n)代替F(μ)的值,可以得到F(x)的表达式:


用阈值模型(PeaksOverThresholdModel,简称POT模型)估计车辆荷载的分布尾部时,关键在于阈值μ的选取。阈值μ太大,将只有很少的超出量样本,估计量的方差会偏高;阈值μ太小,则超出量Y与GPD分布相差较大,估计量成为有偏估计。
2.2阈值选取
阈值μ选取的方法主要有图解法和计算法两大类。图解法是根据平均超出量函数e(μ)的线性变化或判断阈值μ改变所引起的参数估计量的变化来进行阈值的选取。计算法主要有Hill法、峰度法等[11-13]。虽然图解法应用较为广泛,但其存在较强的主观性,因此,本文采用峰度法进行阈值选取,计算步骤如下:
(1)计算样本峰度Kn;
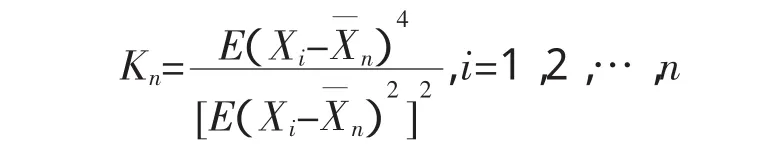
(2)对峰度进行判断,若Kn≥3,则选取使得
(3)重复步骤第一、第二步,直到峰度小于3为止;
(4)在留下来的样本点中选取最大的Xi,此值即为阈值。
2.3参数估计
参数估计即是基于现有的车辆荷载数据去估计POT模型的未知参数,主要有极大似然估计、矩估计、Bayes估计等方法[14]。经对比分析后,选取极大似然法进行参数估计。
假定观测到车辆荷载样本序列X1,X2,…,Xn,用极大似然估计方法对参数ξ和σ进行假设推断。由式(3)两边求导可以得到GPD分布的密度函数:

对式(8)两边求自然对数可得GPD分布的对数极大似然估计函数:
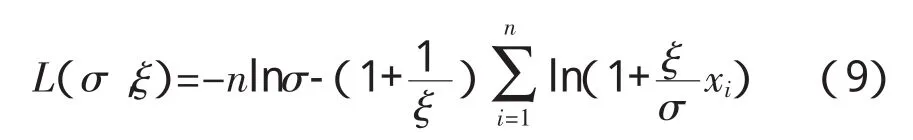
分别对σ和ξ求偏导,并令其等于0,得:

3 实例分析
选取某站点2014年4月份共计30d五型车的车辆荷载为研究对象,共计25952组数据用于实例分析。采用峰度法选择阈值,将五型车数据通过matlabR2010b[15,16]程序运算即可获得阈值μ为76.8,见表1。

表1 峰度法计算的阈值
然后,根据式(10),应用MatlabR2010b程序对GPD分布参数σ和ξ进行估计,估计结果见表2。

表2 参数估计结果
根据参数估计的结果,超阈值数据的峰度远大于正态分布的峰度3,且JB检验的P值为0.001,可以看出阈值超出量不服从正态分布,具有尖峰厚尾性,因此可以利用基于GPD分布的POT模型对数据的尾部进行拟合。根据式(7),可得任意一个五型车总重的分布尾部为:

将五型车总重的尾部分布绘制于图3,由图3可见,分布尾部的实测值与分布尾部的拟合结果符合较好。
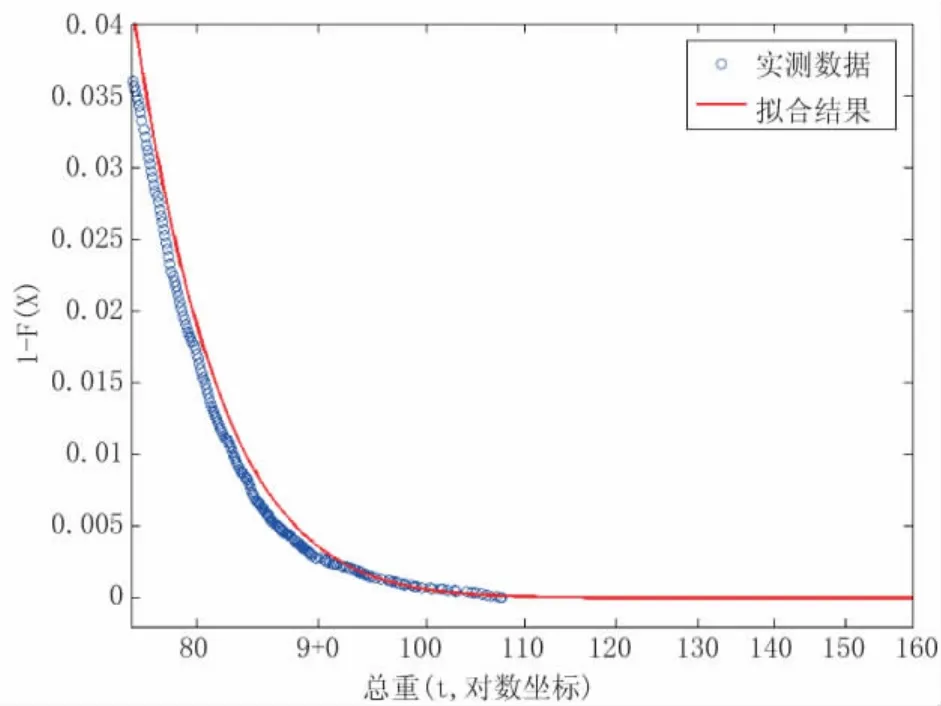
图3 五型车总重的分布尾部的拟合效果
对于车辆荷载整体状况的估计,由全概率公式[17]可得任意一辆重车w的分布函数Fw(x)为:
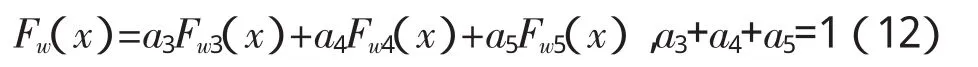
根据多模态变量的极值分析理论[1],对式(12)近似得:
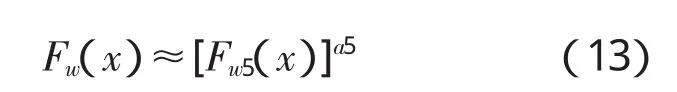
根据广东省京珠高速管理中心近几年来的观测数据,五型车约占所有重车(包括三、四、五型车)总流量的66.5%,因此可取a5=0.665。
如果分析基准期T内的重车总流量为n,那么T内车辆荷载的重现水平U(T),即车辆总重分布的p=1-1/n分位数概率值。而T内车辆荷载的最大值(保证率为95%)为最大重量分布的0.95分位数W0.95,即n辆重车的最大重量分布的p1/a5=(0.951/n)1/0.665= 0.951/0.665n分位数。据此,计算不同基准期T内的车辆荷载重现水平U(T)与最大值W0.95,结果汇总于表3。
从估计结果来看,超过114.8t的重车平均每月会出现一次,超过126.5t的重车平均每年出现一次。对比计重收费政策实施前的重车车重及频次统计情况,说明计重收费政策对超重车辆的总重、出现频次有一定的抑制效果,但并未有效控制超重车辆的变异情况。2008年应天益于对佛开高速公路进行统计分析,外推50a重现期的荷载最大值为156.5t[18],与本文的153.9t非常接近。另一方面,现实车辆荷载已经远远超过了设计荷载标准,对道路桥梁安全正常服役构成了严重的威胁。事实上,在30d的实测数据中,已经出现重达107.9t的车辆,而且,随着重现期的增加,有充分的理由确信还会出现更大重量的车辆荷载。因此,有必要不断改进完善计重收费政策。
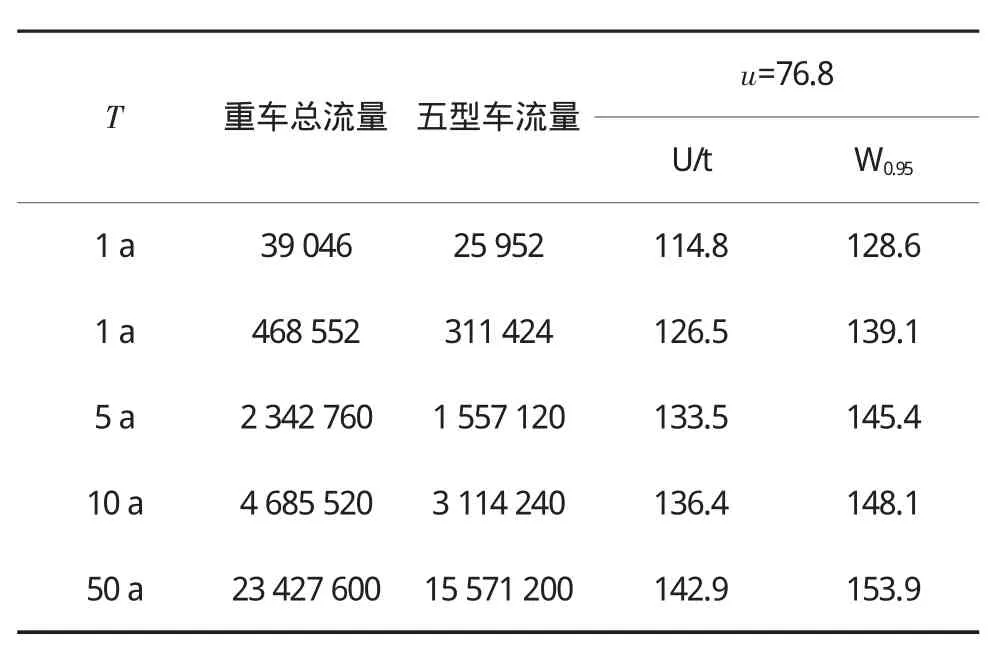
表3 车辆总重的重现水平与最大值
5 结论
本文基于计重收费模式下的WIM实测数据,利用极值理论构建了运营车辆荷载的POT模型,较好地描述了车辆总重分布尾部特征,在此基础上,预测了运营车辆荷载的发展变异趋势。结果表明,超大吨位车辆出现并非偶然,在未来还可能出现更大吨位的车辆荷载,对既有道路桥梁的安全运营构成了严重的威胁。
[1]梅刚,秦权,林道锦,等.公路桥梁车辆荷载的双峰分布概率模型[J].清华大学学报(自然科学版),2003,43(10):1394-1397.
[2]王涛.高速公路桥梁交通荷载调查分析及仿真模拟[D].陕西西安:长安大学,2010.
[3]王涛,韩万水,黄平明.公路桥梁交通荷载研究现状及展望[J].建筑科学与工程学报,2010(4):31-37.
[4]孙吉书,杨春风,窦远明,等.基于交通调查的重载交通公路桥梁设计车辆荷载探讨[J].河北工业大学学报,2009(1):91-95.
[5]贡金鑫,李文杰,赵君黎,等.公路桥梁车辆荷载概率模型研究(一)-非治超地区[J].公路交通科技,2010(6):40-45.
[6]贡金鑫,李文杰,赵君黎,等.公路桥梁车辆荷载概率模型研究(二)--计重收费地区和强制治超地区 [J].公路交通科技,2010(7): 56-60.
[7]史道济.实用极值统计方法 [M].天津:天津科学技术出版社, 2005.
[8]茆诗松,王静龙,濮晓龙,等.高等数理统计[M].北京:高等教育出版社,2006.
[9]ROLFDIDTER,MICHAELT.Statisticalanalysisofextremevalues frominsurance,finance,hydrologyandotherfields[M].Basel: BirdhouseVerlag,2001.
[10]余丹如.公路桥梁活载与活载模型[J].中南公路工程,1992(3): 31-37.
[11]花拥军,张宗益.基于峰度法的POT模型对沪深股市极端风险的度量[J].系统工程理论与实践,2010,30(5):786-796.
[12]DUJing.DiscussonBridgemanagementsystemofsafety assessmentandmaintenancedecisionanalysismethod[D].A DissertationSubmittedfortheDegreeofDoctor,2008.
[13]欧阳资生,龚署明.广义帕累托分布模型:风险管理的工具[J].财经理论与实践(双月刊),2005,26(137):88-92.
[14]高娟.极值分布参数估计方法的研究[D].北京:华北电力大学, 2008.
[15]邓薇.MATLAB函数速查手册[M].北京:人民邮电出版社,2008.
[16]赵海滨.MATLAB应用大全[M].北京:清华大学出版社,2012.
[17]茆诗松,王静龙,濮晓龙,等.高等数理统计[M].北京:高等教育出版社,2006.
[18]应天益.基于WIM数据的桥梁汽车荷载及其效应分析[D].上海:同济大学,2009.
U491.1
A
1009-7716(2016)11-0143-04
10.16799/j.cnki.csdqyfh.2016.11.041
2016-07-13
国家自然科学基金资助项目(51278134);教育部博士点基金项目(20114410110003);广东省交通运输厅科技项目(201402022)
赵高鹏(1988-),男,安徽阜阳人,硕士研究生,从事桥梁结构性能评估与试验研究工作。
