基于多项型高斯函数的过渡段路基沉降预测

王江荣，赵 睿，袁维红，任泰明

（兰州石化职业技术学院，甘肃 兰州730060）

基于多项型高斯函数的过渡段路基沉降预测

王江荣，赵 睿，袁维红，任泰明

（兰州石化职业技术学院，甘肃 兰州730060）

高速铁路过渡段路基沉降是复杂的非线性系统，提高路基沉降的预测精度对于高速铁路建设和运营具有重要意义。利用MATLAB工具箱分别建立路基沉降与累计时间和累计填土高度的单因素高斯型数学模型，通过线性回归分析得到了两个单因素的非线性综合模型。实证分析表明该综合模型具有较高的精确度，预测效果好于BP神经网络模型，能够较好地指导工程建设。

过渡段路基沉降；高斯函数；综合模型；非线性回归；预测

0　引　言

在我国高速铁路路基结构中设置了一个过渡段，该过渡段位于土质路基与刚性结构物之间，它的沉降变形（在纵向是不均匀的）对高速铁路的平顺、安全和耐久性具有控制作用[1-2]。合理地预测过渡段路基的沉降量是高速铁路建设中需要解决的一个重要问题。目前的高铁路基沉降预测方法有BP神经网络[3]、时间序列分析法[4-5]、灰色理论[6]及卡尔曼滤波[7]等方法，这些方法在高铁路基沉降预测方面均取了不错的效果，但也存在着一些不足。BP神经网络具有良好非线性数据逼近能力，适合多因素建模，但存在着对数据质量和数量要求较高的问题，而且运算结果不稳定，容易发生过拟合现象；时间序列分析法、灰色理论与卡尔曼滤波算法更适合因变量（被解释变量）自身间的建模，难以反映解释变量和被解释变量间的关系。本文在已有研究成果的基础上提出了一种确定性多元非线性初等模型——多项型高斯函数综合模型，该模型的优点是解释变量和被解释变量间的依赖关系清晰，计算结果稳定。工程实例分析表明本文所建模型具有较高的精确度，预测效果好于BP神经网络模型，能够满足工程建设需要，具有一定的借鉴意义。

1　基本数据

影响高铁路基过渡段路基沉降的因素有时间、填土高度、填料类型、地基型式、地质环境、至桥台距离和施工等。对于具体工程而言，地质环境和施工影响可看成是相同的；另外填料类型、地基型式和至桥台距离相对施工过程和沉降过程而言可看是不变因素。所以对某观测点来说影响沉降量的变化主要因素是时间和填土高度。文献[8]给出了津秦客运专线路桥过渡段某监测点的一组沉降数据，见表1。

将表1中序号1～26即前26组数据作为建模样本，序号27～34即后8组数据作为测试样本，进行建模及模型检验。

2　多元非线性回归模型建立

设解释变量x1=累计时间（d），x2=累计填土高度（m），被解释变量y=累计沉降量（mm）。

按如下步骤完成模型建立：

（1）分别建立被解释变量y对解释变量x1和x2的两个单因素非线性回归模型，分别记作y1=f1（x1）和y2=f2（x2）。

（2）建立被解释变量y对y1和y2的二元线性回归模型：y=ay1+by2+c（a，b，c为回归系数），进而得到非线性回归模型，并对所建模型进行检验。

2.1单因素非线性回归模型

（1）路基沉降量与时间因素的非线性回归模型

利用表1前26组数据（时间-累计沉降量）建模。利用MATLAB曲线拟合工具箱cftool（cure fittingtool）容易得到二项型高斯曲线的判定系数R2=0.9964（调整的决定系数R2=0.9957），均方根误差RMSE=0.2749，残差平方和SSE=2.115。模型性能指标表明模型拟合效果显著，见图1。

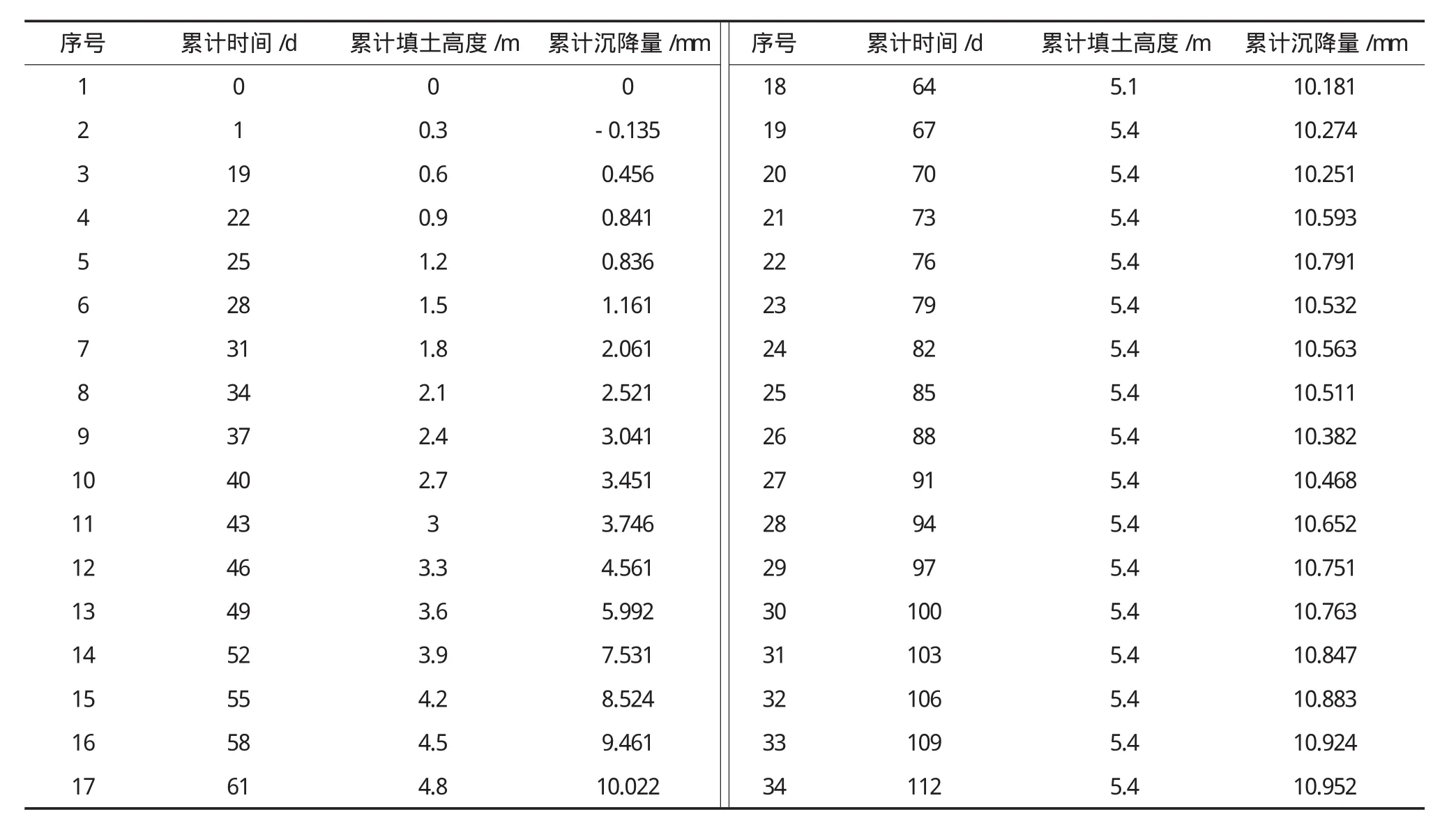
表1　沉降数据[8]

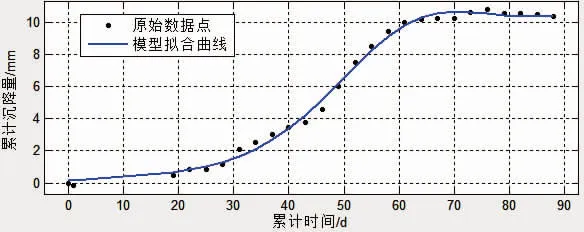
图1　二项型高斯模型的时间-沉降量拟合曲线

建立的二项型高斯时间-沉降量的一元非线性回归模型为：

说明一点，对于不同的沉降问题可按拟合优度值（R2越接近1越好）选用一项型、二项型或三项型等高斯模型进行数据拟合及预测。

（2）路基沉降量与累计填土高度因素的非线性回归模型

利用表1前26组数据（累计填土高度-累计沉降量）建模。利用MATLAB曲线拟合工具箱cftool（cure fittingtool）容易得到一项型高斯曲线的判定系数R2=0.9951（调整的决定系数R2=0.9948），此时的均方根误差RMSE=0.3029，残差平方和SSE=2.845。模型性能指标表明模型拟合效果显著，见图2。

图2　一项型高斯模型的填土高度-沉降量拟合曲线

建立的一项型高斯填土高度-沉降量的一元非线性回归模型：

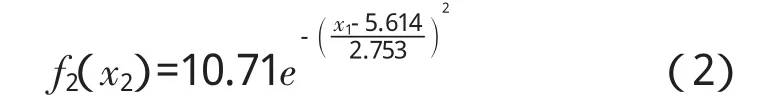
2.2二元非线性回归模型

建立累计沉降量y对f1（x1）和f2（x2）的线性回归方程：y=af1（x1）+bf2（x2）+c。利用MATLAB提供的regstats函数[9]计算回归系数，并对回归方程进行显著性检验。得到的二元线性回归方程为：

模型显著性检验：决定系数R2=0.9964，调整的决定系数R2=0.9962，均方根误差RMSE=0.2596，方差分析中的p≤0.0001，说明模型（3）是极显著的，拟合效果非常好，可以用以路基沉降预测。

将式（1）和式（2）代入式（3）得累计沉降量（y/mm）关于累计时间（x1/d）因素和累计填土高度（x2/m）因素的多元非线性回归方程：

3　模型检验

将表1中的检验数据（序号27～34的因素指标：累计时间及累计填土高度）代入模型（4）可得累计沉降量的预测值，结果见表2。

表2　测试数据累计沉降量的预测值

从表2给出的平均绝对误差和平均相对误差可看出，本文建立的多项型高斯函数路基沉降回归模型具有较高的预测精度，和文献[8]给出的BP神经网络预测结果相比本文模型预测效果更好，预测精度得到了显著提高。另外，多项型高斯路基沉降回归模型还具有结构简单、可操作性强、解析式清晰和运算结果稳定的优点（神经网络结构复杂，变量间的依赖关系不明晰，运算结果不稳定）。

4　结　语

本文选取影响高速铁路过渡段路基沉降的两个动态因素即累计时间和累计填土高度建立了多项型高斯函数路基沉降预测模型。首先利用MATLAB曲线拟合工具箱分别建立了路基沉降量与时间因素的高斯型函数模型和路基沉降量与填土高度因素的高斯型函数模型，然后利用MATLAB统计工具箱建了这两个单因素模型的组合模型。两个单因素模型分别揭示了它们与路基沉降之间的内在联系，它们与路基沉降间有着很强的非线性关系。组合模型是两个单因素模型的综合体，它是两个动态因素对路基沉降的综合反应。工程实例分析表明基于累计时间和累计填土高度的多项型高斯组合模型具有较高的精确度，预测效果好于BP神经网络，而且模型结构简单、解析式明确，具有很强的可操作性，完全可用以指导高速铁路建设。另外，整个建模过程可在MATLAB工具箱内完成，该建模方法可供工程技术人员借鉴。

[1]余泽西,李成辉,王小韬.高速铁路线路过渡段动态不平顺研究[J].中国铁路,2009(4):55-57.

[2]郝建芳.高速铁路路桥过渡段轨道动力特性分析及优化设计研究[D].北京:北京交通大学,2014.

[3]魏 静,蒲兴波,钱耀峰,等.基于动量BP算法的过渡段路基沉降预测[J].北京交通大学学报,2012,36(1):52-55,62.

[4]王刘准,邱卫宁,花向红,等.小波时间序列分析在高铁沉降变形中的应用[J].测绘地理信息,2013,38(40):45-47,51.

[5]刘 闯,花向红,赵杰.基于小波去噪的高铁沉降预测模型研究[J].测绘地理信息,2015,40(1):37-40.

[6]王富麟.改进BP算法的灰色神经网络模型在高铁沉降预测中的应用研究[D].江西南昌:江西理工大学,2013.

[7]陈大勇,刘大伟.卡尔曼滤波法在城际高铁沉降变形监测与分析的应用[J].测绘与空间地理信息,2015,38(6):183-185.

[9]谢中华.MATLAB统计分析与应用40个案例分析[M].北京:北京航空航天大学出版社,2010.

U416.1

A

1009-7716（2016）11-0135-03

10.16799/j.cnki.csdqyfh.2016.11.038

2016-05-17

兰州市科学技术局计划项目（兰财建发[2015]85号）；兰州石化职业技术学院科技资助项目（院发〔2015〕69号）；甘肃省科技厅计划项目（1204GKCA004)；甘肃省财政厅专项资金立项资助（甘财教[2013]116号）

王江荣（1966－），男，甘肃静宁人，教授，从事路基沉降、控制理论与应用方面的教学、研究工作。