学生个体与监考人员间的博弈模型建立

卫思彤

鞍山市鞍钢高级中学

学生个体与监考人员间的博弈模型建立

卫思彤

鞍山市鞍钢高级中学

本文将运用博弈和演化手段，通过构建考生个体与监考人员间的博弈模型，和考生群体在学校对监考人员采取不同激励政策的条件下的演化模型，研究在一定条件下激励政策与作弊人数比例间的关系。

学生个体；监考人员；博弈

一、问题引入及研究思路

考试是教学过程中的一个重要环节，考试作弊现象伴随着考试制度的出现而出现，在各高等院校均有不同程度的存在，且有愈演愈烈的趋势。除去考生自身方面的因素，如学业外的其它琐事分散了时间和精力等，影响考生个人是否作弊之外，还有另一个重要的影响因素是监考人员(考场老师)对参与考试的所有考生的统一监考策略。具体分析如下：

一方面是学生个人与监考人员的博弈。作弊在一定条件下会使考生获得更高收益，例如得到更高分数；同时也有一定风险被监考人员发现并除以责罚。作为经济人，每位考生都将时刻遵循收益最大化原则做出决策，即自己承担最小风险及付出最低成本以获取最大收益。因此考生是否选择作弊及选择使用何种作弊手段将直接被监考人员的监考策略影响。监考人员采取两种监考策略“严格监考”与“不严格监考”，和考生采取两种应对策略“作弊”与“不作弊”及“作弊”策略中的三种作弊手段“手机作弊”“打小抄”“抄同学”，双方都不能通过单独改变策略或概率以改善自身的期望得益，因此构成混合策略纳什均衡，也是该博弈模型的唯一纳什均衡解。

另一方面是学校管理层给予监考人员一定激励机制。监考人员采取两种监考策略“严格监考”与“不严格监考”的意愿直接决定于学校管理层给出的对激励其监考严格的机制，显然激励程度越高或称为强策略(通常表现在更高的报酬﹑更优的评级)，监考人员“严格监考”意愿越强烈即概率越大，考生作弊被发现风险越高，考生收益下降甚至为负。激励程度越低则恰恰相反。因此单个考生的作弊决策也间接受学校管理层制定的激励机制的影响。

二、博弈建立

1.博弈过程说明

t=0时，学校管理层给出激励政策直接决定监考人员收益类型。在这里，假设学校采取强激励策略的概率为θ，弱激励策略的概率为1-θ。因此也可将θ视为激励强度，此处θ可视为博弈过程中的外生变量，它影响模型中其他变量的值，但不受其他变量的影响。则θ可以作为考生与监考人员的共同信息，即学校管理层的激励政策完全对另外两方公开。因此考生能够确定本场考试中所遇到的监考人员是何种收益类型的概率，虽然考生并不能确定监考人员的具体收益类型。

t=1时，监考人员进入考场的同时向考生给出其监考策略“严格”(t1)或“不严格”(t2)，此步骤对应的实际现象是，考生可以在监考人员进入考场的几分钟及考试开始不久的短暂时间内，通过对监考人员言语和行为判断出监考人员是否严格。

t=2时，选择作弊的学生给出对应的作弊策略：“手机作弊”(s1)，“打小抄”(s2)，“抄同学”(s3)，此博弈可进行重复博弈分析，即可在充分多次博弈后得到最佳混合策略。

2.符号说明

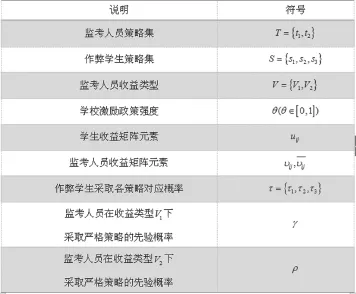
表1

3.模型过程具体分析

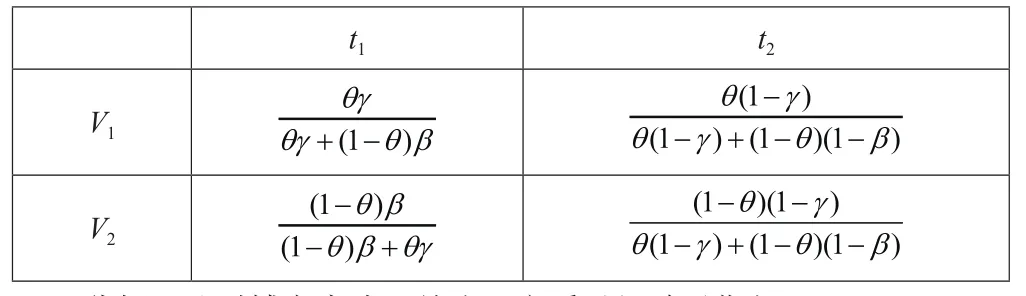
t1 t2 V1V2

分析，此时博弈完成，给出双方受益矩阵及期望。

3.1 学生收益矩阵及期望

(1)T=t1，即监考人员采取严格策略，又在重复博弈中，监考人员采取严格策略的概率为，则。

(2)T=t2，即监考人员采取非严格策略，又在重复博弈中，监考人员采取不严格策略的概率为则学生收益期望为

3.2 监考人员收益矩阵及期望

(1)监考人员收益类型为V1，此时。所以期望为

(2)监考人员收益类型为V2，此时所以期望为

综上

至此，博弈建立完成。

三、结语

文章通过构建考生个体与监考人员间的博弈模型，和考生群体在学校对监考人员采取不同激励政策的条件下的演化模型，结合数理推到与统计结果，经过计算机的演化模拟，最终得到作弊人数N关于激励强度 的关系。

此结果对于学校的实际参考意义是：

(1)提供一个有价值的，能够作为参考让学校决定控制作弊人数手段的模型。论文中各项参数皆可通过统计学方法得到，学校可以用此模型从管理层面得到控制作弊人数在一定范围内的最经济手段。

(2)说明学校需要将激励政策强度控制在一定范围，当激励政策达到一定强度时，学校若继续加强，只会造成成本的浪费。即模型中激励政策的调节函数与横轴有交点。

[1]于久洪，张剑.基于贝叶斯博弈的银行贷款定价研究；统计与决策，2010，(7)

[2] Gy¨orgy Szab´o, Kinga S. Bod´o, Benjamin Allen, and Martin A. Nowak.Four classes of interactions for evolutionary games; Physical Review E 92, 022820 (2015)