基于改进迭代模型的车-桥耦合系统竖向随机振动研究

朱志辉，王力东，龚 威，余志武,2，蔡成标

(1.中南大学 土木工程学院，湖南 长沙 410075；2.中南大学 高速铁路建造技术国家工程实验室，湖南 长沙 410075；3.西南交通大学 牵引动力国家重点实验室，四川 成都 610031)



基于改进迭代模型的车-桥耦合系统竖向随机振动研究

朱志辉1,2†，王力东1，龚 威1，余志武1,2，蔡成标3

(1.中南大学 土木工程学院，湖南 长沙 410075；2.中南大学 高速铁路建造技术国家工程实验室，湖南 长沙 410075；3.西南交通大学 牵引动力国家重点实验室，四川 成都 610031)

采用改进的车-桥耦合系统迭代计算模型，建立了基于虚拟激励法(PEM)的列车-轨道-桥梁竖向随机振动分析模型.采用虚拟激励法将轨道不平顺精确地转化为一系列竖向简谐不平顺的叠加，并运用分离迭代法求解车-桥耦合系统振动方程.以CRH2高速列车通过5跨简支梁桥为例，对改进的车-桥耦合系统迭代计算模型的计算精度和效率进行了验证．结果表明：在保持与传统模型相同计算精度的前提下，改进模型能使计算效率提高5倍左右.通过对列车-轨道-简支梁桥竖向随机振动响应中确定性激励引起的均值和轨道不平顺引起的均方根进行分析可知：桥梁竖向位移主要受列车自重控制，轨道不平顺引起的桥梁竖向位移影响很小；桥梁和车体竖向加速度受轨道不平顺影响显著，改善线路条件能有效提高列车的乘车舒适性；同时，车速越高，桥梁和车辆随机响应的均方根越大，由轨道不平顺引起的耦合系统振动响应的离散度越大.

车-桥耦合振动;迭代模型;赫兹接触;虚拟激励法;简支梁桥

在车-桥耦合系统动力响应研究中，轨道不平顺是引起耦合系统振动的重要激励源.由于轨道不平顺是一个近似各态历经的随机分布，由此引起的车-桥耦合振动也是一个典型的随机过程[1].潘家英[2]在分析列车通过广西红水河铁路斜拉桥的动力响应时发现，桥梁结构动力响应主要随车速及轨道不平顺样本函数的不同而变化，且具有较大的随机性.夏禾[3]选取20个激励样本对车辆通过单跨桥梁时的系统响应进行统计分析，发现桥梁跨中横向振幅和机车车体横向振动加速度变异系数分别高达38%和23.7%.因此开展基于随机振动方法的车-桥耦合振动研究对准确评估车-桥耦合振动特性显得尤为重要.

在车-桥耦合系统随机振动研究中，计算效率和计算精度一直都是制约该问题研究的重要因素.传统随机振动研究常用的Monte Carlo法是一种基于大样本容量的随机分析方法，必须取足够数量的样本才能保证统计结果的可靠性[4].为降低随机振动分析的计算量，同时提高随机振动分析的准确性，林家浩[5]提出了随机振动的虚拟激励法，其特点是将平稳随机响应分析转化为谐响应分析，将非平稳随机响应分析转化为时间历程分析，并广泛应用于航空、地震、风等多领域的研究工作.同时，LV[4],ZHANG[6],李小珍[7]等将虚拟激励法用于车-桥耦合振动，研究了列车荷载作用下车辆-简支梁桥和连续梁桥耦合系统的随机振动特性.在这些研究中，为简化所分析问题的难度，通常假定钢轨与桥面之间无相对运动，忽略了轨道结构弹性变形作用.

随着研究的逐步深入，轨道结构的弹性支承和变形作用在车-桥耦合振动中的影响逐步引起了研究人员的重视[8-9].但当车-桥耦合振动研究考虑轨道结构时，会使以往基于分离迭代方法的耦合系统动力方程计算效率、收敛性和计算精度问题变得更为重要.吴定俊[10]、杜宪亭[11]等分别针对轮轨弹性接触模型和密贴模型，讨论了分离迭代算法的数值求解稳定性问题.研究结果表明虽然轮轨弹性模型在足够小的时间积分步长下可以收敛，但会导致计算时间过长；同时，当采用轮轨密贴模型时，由于簧下车轮质量大于轮轨接触点处钢轨质量，从而导致密贴模型计算不收敛.ZHANG[12]、杜宪亭[13]为提高车-桥耦合系统动力方程求解效率，分别提出了全过程迭代法和精细Rung-Kutta混合积分法，但上述研究并未考虑轨道结构对计算方法的影响.

针对车-桥耦合系统随机振动研究中存在的计算效率和迭代计算收敛性问题，本文首先建立了改进的列车-轨道-桥梁耦合系统迭代计算模型，并通过谱半径理论和数值算例对比分析了改进迭代计算模型的迭代稳定性和精度.其次，推导了基于改进迭代计算模型和虚拟激励法的车-轨-桥耦合系统随机振动分析方法.以高速列车通过简支箱梁桥为算例，分析了高速列车-轨道-桥梁耦合系统竖向随机振动响应特征，讨论了车速、轨道不平顺以及轨道结构的影响规律.

1 改进的车-桥系统迭代计算模型

基于迭代算法的车-桥耦合振动分析模型通常以轮轨接触面为界，分为车辆子系统和桥梁子系统两部分，每个子系统的组成如图1(a)所示.依据D’Alembert原理，图1(a)中基于平衡位置的车体轮对质量块的动力平衡方程可以表示为：

(1)

kh(ut+uir-uw)

(2)

轮下质量块的动力平衡方程可以表示为：

(mw+mv)g

(3)

式中:m,c,k分别表示质量、阻尼、刚度，u表示位移；下标v,w,t分别代表车体质量块、轮对质量块、轮下质量块；下标p代表车辆悬挂系统，ir代表轨道不平顺；kh为轮轨接触刚度系数，g为重力加速度.

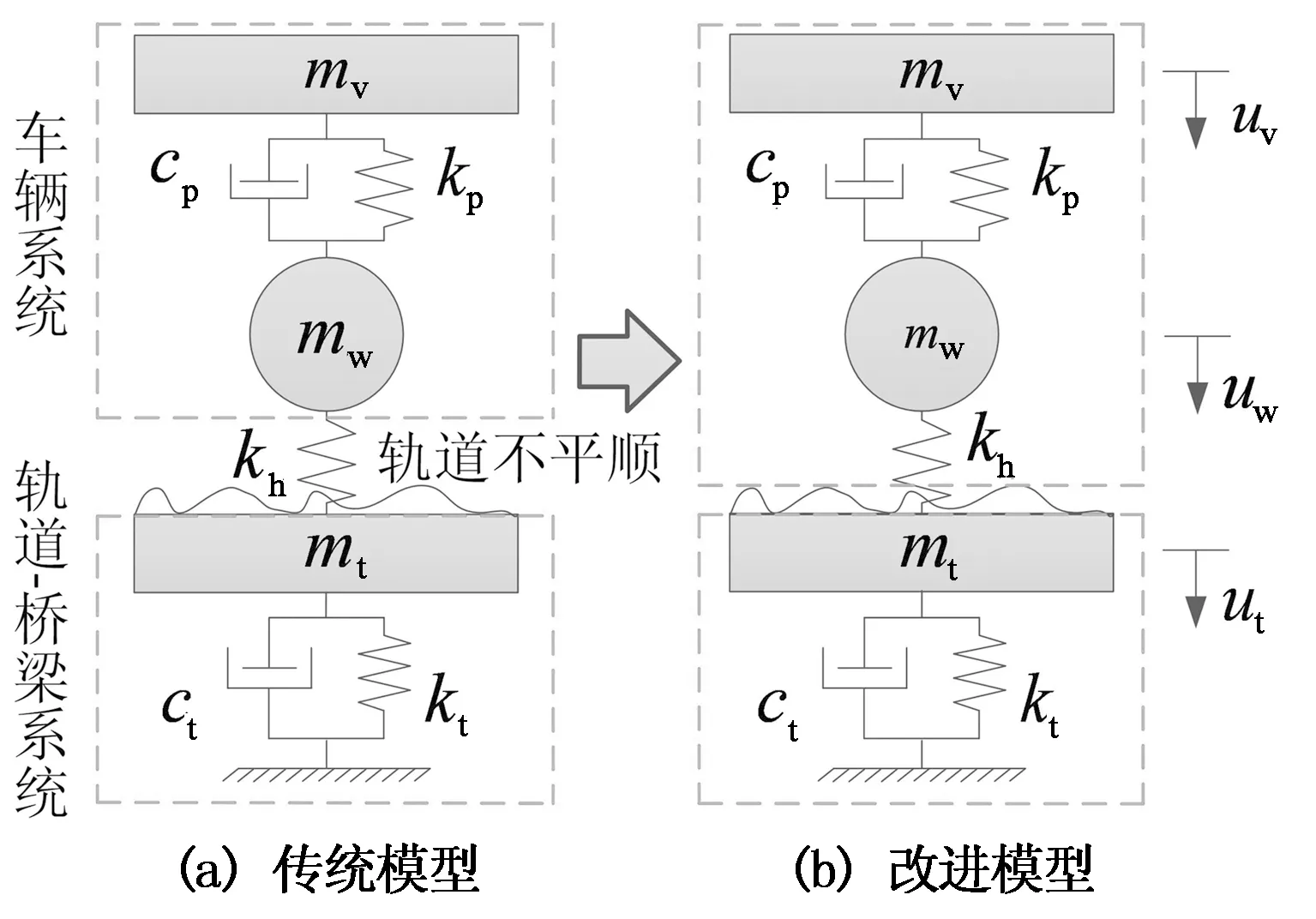
图1 简化的轮轨线性赫兹接触车-桥系统Fig.1 Simplified train-bridge system under the wheel-rail linear Hertz contact

根据文献[10]可知，在传统的车-桥耦合系统迭代计算模型中，车辆系统的迭代稳定性在车-桥耦合振动问题中起控制作用.由于轮轨间接触刚度kh通常在109N/m，为保证车-桥耦合系统迭代计算的收敛性，时间积分步长一般在10-5s；同时，当考虑轨道结构时，mw通常大于mt，很难保证收敛.

为提高传统迭代计算模型的计算效率，本文建立了改进的车-桥耦合系统迭代计算模型(Improved iteration model for train-bridge coupled system, IIM)，如图1(b)所示.通过建立包含轮轨接触弹簧kh的车辆模型来提高车辆系统的迭代稳定性.

相对于传统车-桥耦合系统迭代计算模型，图1(b)所示改进模型的轮对质量块动力平衡方程为：

kh(ut+uir)

(4)

改进模型在时间步t上第k次和第k+1次迭代之间的直接迭代格式为：

(5)

(6)

(7)

1.1 谱半径分析

对于车-桥耦合迭代计算模型，可以通过建立耦合系统动力方程前后迭代步之间的递推关系，根据迭代矩阵谱半径的大小来判断迭代计算稳定性[10].以Newmark-β法数值积分格式为例，根据式(5)～(7)可建立改进模型在t时刻上的迭代计算格式如下：

Xk+1=MXk+f(t)

(8)

式中:

(9)

上标T表示转置，M为迭代矩阵，其非零元素为：

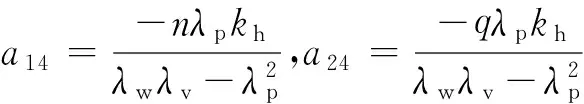
(10)

其中，

λv=mv+qcp+nkp;λt=mt+qct+nkt;

λw=mw+qcp+nkp+nkh;

λp=qcp+nkp;n=βΔt2;q=γΔt

(11)

常数项f(t)为上一时间步系统运动状态、轨道不平顺以及车辆重力的函数，因与收敛性无关，无需给出具体形式.

通过求解迭代矩阵M的特征值多项式，得相应的谱半径为：

(12)

其中，

(13)

通过与上述类似的分析过程，可得传统模型的迭代矩阵谱半径如下：

(14)

其中，

(15)

根据一般高速列车的车辆参数，可以近似假定图1所示的简化模型系统参数为：mv=6 800kg,mw= 1 200kg,mt=36kg,kp=1.04×106N/m,cp=4.0×104N·s/m,kt=1.6×108N/m,ct=5.2×106N·s/m,kh=1.35×109N/m.根据式(12)和式(14)可绘出如图2所示的改进模型和传统模型的迭代矩阵谱半径随积分步长的变化规律.

从图2中可以看出，改进模型和传统模型的迭代矩阵谱半径随积分步长的变化规律具有完全不同的变化趋势.传统模型的谱半径随着积分步长的增大呈开口向上的抛物线形递增；改进模型的谱半径随积分步长的增大以较为缓慢的趋势递增，且相同积分步长下改进模型的谱半径均小于传统模型.

积分步长/(10-3·s)图2 改进模型和传统模型谱半径随积分步长变化规律Fig.2 The change rule of the spectral radiusof the improved model and the traditionalmodel with the integral step

1.2 线性赫兹接触刚度

针对线性赫兹接触刚度系数kh，目前主要有两种取值方法，分别是切线斜率法[14]和割线斜率法[15].

1.2.1 切线斜率法

切线斜率法是指过非线性赫兹接触刚度曲线中静态轮轨力P0对应的A0点作切线，切线的斜率即为kh的取值，如图3虚线所示.

轮轨压缩量/mm图3 非线性和线性赫兹接触曲线Fig.3 Nonlinear and linear Hertz contact curve

根据非线性赫兹接触理论，轮轨竖向作用力P(t)与轮轨弹性压缩量δZ(t)之间存在如下关系：

(16)

式中G为轮轨接触常数(m/N2/3).

根据式(16)，可以求得A0点切线的斜率，即

(17)

其中δZ0(t)是静态轮轨力P0对应的轮轨静压缩量.

1.2.2 割线斜率法

割线斜率法是指取非线性赫兹接触曲线中静态轮轨力P0对应的A0点和轮轨力变化范围常见最大值P1对应的A1点的连线的斜率作为kh的取值，如图3点画线所示.根据A0点的坐标(GP02-3，P0)和A1点的坐标(GP12-3，P1)，可得A0点和A1点连线的斜率为

(18)

2 车-桥竖向耦合系统随机振动分析

2．1 基于IIM的车辆模型

基于IIM的车辆模型如图4所示，每节车辆由1个车体、2个转向架和4个轮对组成，且均视为刚体，转向架和轮对之间通过一系悬挂连接，车体和转向架之间通过二系悬挂连接，悬挂系统均视为线性系统.每节车共10个自由度，包括车体、转向架的沉浮(Zc,Zt1,Zt2)和点头(βc,βt1,βt2)以及轮对的沉浮(Zw1,Zw2,Zw3,Zw4).轮轨之间通过线性赫兹接触弹簧kh联结.

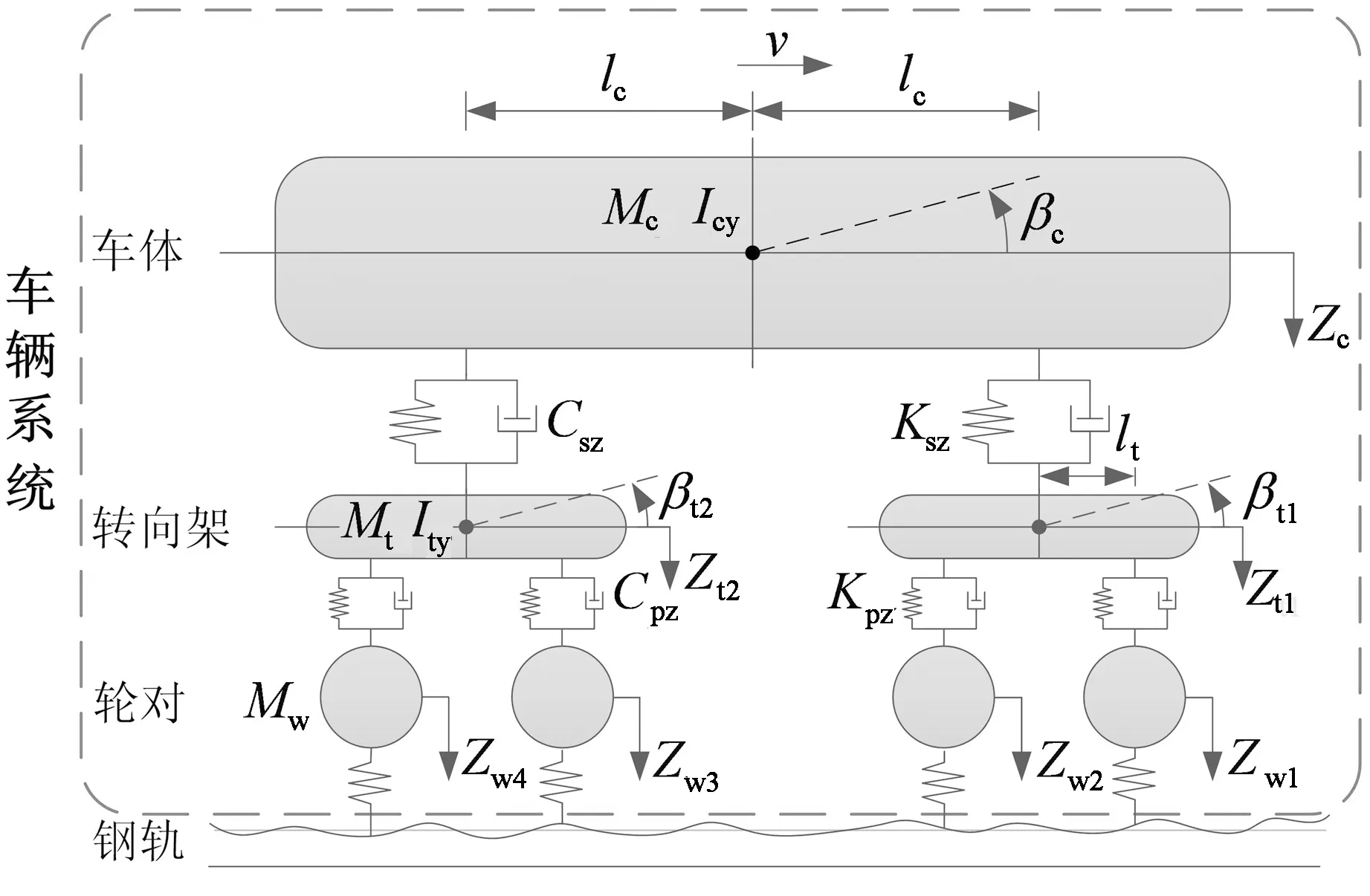
图4 基于IIM的车辆模型Fig.4 Vehicle model based on IIM

采用D’Alembert原理，可建立基于平衡位置的车辆运动方程如下：

(19)

式中:MV,CV,KV分别为车辆的质量矩阵、阻尼矩阵、刚度矩阵；UV和FV分别为车辆的位移向量和力向量.UV,MV,KV,FV的具体表达式如下：

(20)

(21)

(22)

其中，

(23)

式中，Zri(t)和ri(t)分别为第i(i=1～4)个轮对轮轨接触处的钢轨竖向位移和轨道不平顺附加位移.

由于除轮轨接触弹簧kh外，车辆的阻尼元件和弹簧元件布置方式相同，因此CV的表达式只需去掉KV中的kh，然后将K改为C即可.通常，列车由多节车辆编组形成，由于各节车辆相互独立，可采用“对号入座”法则建立列车的运动方程.

(24)

2．2 轨道-桥梁模型

轨道桥梁系统运动方程可表示如下：

(25)

式中:MB,CB,KB分别为轨道桥梁系统的总体质量矩阵、总体阻尼矩阵和总体刚度矩阵；UB和FB分别为轨道桥梁系统的位移向量和力向量.由于本文仅考虑车辆引起的车-桥耦合振动，因此外荷载项FB(t)中仅包含车辆对轨道的作用力.其中，车辆各轮对作用于轨道的轮轨力可表示为：

(26)

2．3 基于虚拟激励法的车-桥耦合系统随机振动分析

受轨道高低不平顺随机激励的车-桥竖向耦合系统运动方程可以写成如下形式[4]：

F1(t)+F2(t)

(27)

式中:M,K,C为耦合系统整体质量、刚度、阻尼矩阵；F1(t)为车辆自重引起的确定性激励；F2(t)为轨道高低不平顺引起的非平稳随机性激励.

实际线路上存在的轨道不平顺是由不同波长、不同相位和不同幅值的随机不平顺波叠加而成的.它是一个近似各态历经的弱平稳过程，而对局部不平顺来说，又是一个非平稳过程.因此，对于随机性激励F2(t)，可将其表示为如下形式：

F2(t)=Γ(t)G(t)x(t)

(28)

(29)

(30)

其中，Γ(t)为作用力指示向量，G(t)为慢变均匀调制函数矩阵，x(t)为轨道不平顺引起的多点异相位平稳随机激励向量，n为列车轮对总数.

由于假设轨道不平顺为零均值平稳随机过程，因此系统随机响应均值μu是由确定性激励F1(t)引起的[4]，而随机性激励F2(t)可以构造为均匀调制多点异相位非平稳随机响应的虚拟激励：

(31)

(32)

(33)

从而可快速获得系统随机响应的功率谱密度矩阵：

(34)

其中，

(35)

式中:h(t-τ,τ)为脉冲响应函数，Sxx(ω)为x(t)的自谱密度矩阵.最后，根据随机响应的功率谱密度矩阵，可通过下式求得系统随机响应的均方根：

(36)

其中，Δω为频率增量.

考虑由车轮间距所产生的轮轨间随机激励的相位差，第j(j=1～n)轮对由轨道不平顺引起的虚拟轨道不平顺rj可以表示为：

(37)

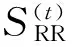
(38)

式中，ω为轨道不平顺的时间圆频率，单位rad/s；λ为轨道不平顺函数谐波分量的波长，单位m.

因此，第j轮对所受虚拟轮轨力为：

(39)

相应的，第j轮对作用于钢轨的虚拟轮轨力为：

(40)

工程设计中，结构响应的最大值往往是主要关注对象，本文采用3σ法则(即μu±3σu)确定车-桥耦合系统中桥梁和车辆随机响应的上下限值.

3 计算模型及验证

3.1 基本参数

以我国高速线路总里程中比例最大的32m预应力混凝土简支箱梁桥为研究对象，建立如图5所示的轨道-桥梁子系统有限元模型.桥梁模型按5跨简支梁建立，墩高为18m，主梁和桥墩截面如图6所示.

图5 轨道桥梁模型Fig.5 Track-bridge model

图6 桥梁截面示意图(单位：mm)Fig.6 Schematic diagram of bridge (unit:mm)

有限元模型中，主梁和桥墩均采用空间梁单元离散；钢轨采用空间梁单元离散，并通过刚臂考虑线路偏心[16].钢轨节点和刚臂节点之间通过弹簧-阻尼器联结，考虑轨下扣件和垫板的弹性支撑作用，竖向刚度和阻尼分别为4.76×107N/m和7.5×104N·s/m，横向刚度和阻尼分别为2.5×107N/m和6×104N·s/m，桥面二期恒载取160kN/m.全桥节点数共计2 540个，单元数共计6 834个.

选取我国CRH2高速列车按8车编组形成车辆系统，具体车辆参数见文献[17].轨道不平顺谱函数则根据我国规范《高速铁路无砟轨道不平顺谱》(TB/T33522014)的规定，采用分段拟合方式给出了适用于我国线路速度300～350km/h的高速铁路无砟轨道不平顺谱，具体拟合公式如下：

(41)

式中：f为空间频率；A,k为拟合公式系数.本文计算中取轨道高低不平顺作为轮轨竖向激扰，其分段拟合系数如表1所示.

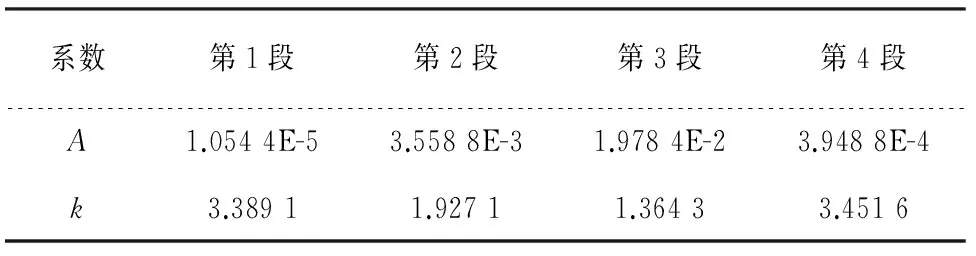
表1 轨道高低不平顺功率谱拟合公式系数Tab.1 Fitting formula coefficient of track vertical profile irregularity PSD

图7(a)和(b)分别给出了轨道高低不平顺功率谱密度曲线和采用三角级数法[3]生成的不平顺样本曲线.同时，为模拟列车进入桥梁之前的初始振动状态，计算时假定列车从距桥头40 m处开始匀速运动.

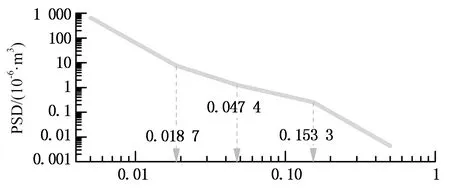
空间频率/m-1(a) 功率谱密度曲线

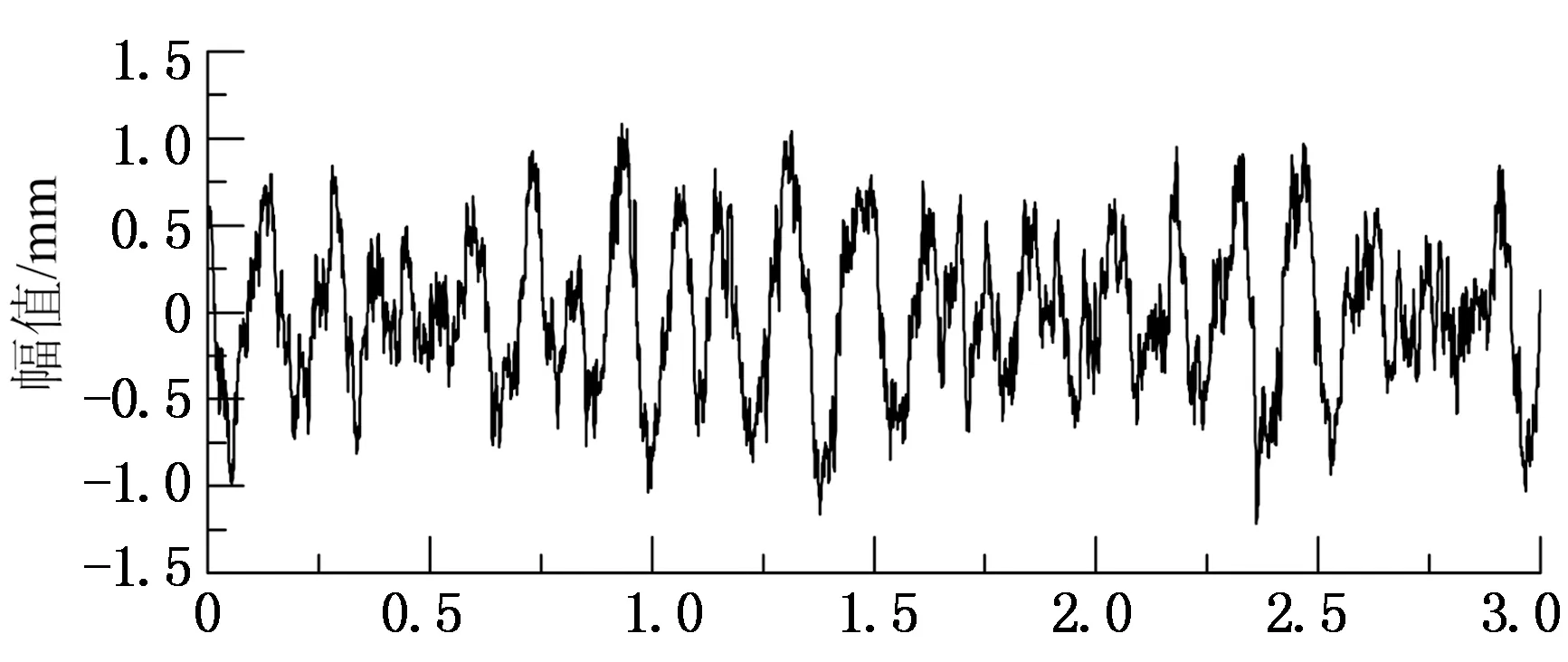
里程/km (b) 样本曲线图7 轨道高低不平顺Fig.7 Track vertical profile irregularity

3.2 改进模型的计算精度和效率

根据车-桥耦合振动的虚拟激励法原理可知，单次计算的精度和效率是整个随机计算过程的基础.为验证IIM的计算结果和效率，本文采用如表2所示的4种不同的轮轨接触模型开展车-线-桥竖向耦合振动分析.其中，基于切线斜率法的动车和拖车的

轮轨接触刚度分别为1.44×109N/m和1.38×109N/m；基于割线斜率法的动车和拖车的轮轨接触刚度分别为1.53×109N/m和1.47×109N/m，即取P1=1.45P0[18].车速设为300 km/h，轨道不平顺样本值如图7(b)所示.同时，本文所有计算均在64位8线程Intel Core i74790K(4.00 GHz,16 G内存)计算机上完成.

表3给出了不同轮轨接触模型计算得到的车-线-桥系统竖向响应最大值及计算效率对比.从表3中可以看出，4种模型计算结果均吻合较好，其中钢轨加速度的误差为8.6%，表明切线斜率法和割线斜率法得到的线性化轮轨接触刚度具有较高的计算精度.另一方面，由于通过切线斜率法得到的轮轨接触刚度小于割线斜率法，因此CTH模型和NTH模型计算的钢轨振动加速度均小于CSH模型和NSH模型.和传统迭代计算模型相比，改进的迭代计算模型具有更高的计算效率，可以使计算时间缩短5倍左右.

表2 轮轨接触模型Tab.2 Wheelrail contact model

表3 不同轮轨接触模型下车-线-桥系统竖向响应最大值及计算效率对比Tab.3 Comparing maximum value and computation efficiency of train-uack-bridge system vertical response with different wheelrail contact models

3．3 轨道结构对车-桥系统随机响应影响

在车-桥耦合振动研究中，轨道结构为上部车辆提供支撑和弹性减振作用.为分析轨道结构对车-桥耦合系统竖向随机振动的影响，本文建立了如表4所示的两种车-桥耦合系统计算模型，并采用虚拟激励法计算两种模型在相同计算条件下的随机响应.当不考虑轨道结构时，将轨道结构以参振质量形式在桥梁自重中加以考虑，其余计算条件不变.

表4 车-桥耦合系统计算模型Tab.4 Calculation model of train-bridge coupled system

表5给出了两种计算模型下桥梁和车辆随机响应最大值.从表5可以看出，轨道结构对桥梁和车辆随机响应影响较为显著.当考虑轨道结构时，由于轨道结构刚度的影响，中跨桥梁跨中竖向位移均值、均方根和限值均比不考虑轨道结构的模型2分别减小42.9%,9.5%和41.8%；同时，在列车动力荷载作用下，轨道结构自身的变形会增加轨面的动态不平顺度，加剧车辆对桥梁结构的动力作用，从而使中跨桥梁跨中竖向加速度均值、均方根和限值比模型2分别增大12.2%,24.1%和17.4%.相比动车，拖车车体竖向加速度均值和限值受轨道结构影响较显著，模型1比模型2分别减小62.5%和5.4%；均方根值则变化不大.因此，为得到更为合理的仿真结果，车-桥耦合振动模型中应该考虑轨道结构的影响.

表5 两种计算模型下桥梁和车辆竖向随机响应最大值Tab.5 Maximum value of vertical random response of bridge and train under two types of calculation models

4 车-桥耦合系统随机响应分析

4.1 振动响应特征分析

基于IIM和切线斜率法的轮轨线性赫兹接触，本文开展了列车-轨道-简支梁桥竖向随机振动分析.车速为300 km/h，不平顺空间频率范围取0.005～0.5(1/m)，并离散为100个频点.图8～图10分别给出了中跨桥梁跨中竖向位移、竖向加速度和动车车体竖向加速度的均值、均方根和上、下限值时程曲线.

从图8可以看出，中跨桥梁跨中竖向位移均值和均方根最大值分别为0.8 mm和0.001 mm左右，两者相差近80倍；同时，由3σ法则得到的桥梁上、下限值十分接近.由此说明，桥梁竖向位移主要受车辆自重控制，轨道不平顺对其影响很小.从图9可以看出，中跨跨中桥梁竖向加速度均值和均方根最大值分别在0.45 m/s2和0.12 m/s2左右，两者处于同一数量级，前者为后者的4倍.表明在轨道不平顺的影响下，桥梁竖向加速度离散度大，其受轨道不平顺的影响显著，改善线路条件能有效减低桥梁振动加速度.

从图10可以看出，动车车体竖向加速度均值和均方根最大值分别在0.03 m/s2和0.037 m/s2左右，后者略大于前者.由此可知，动车车体竖向加速度响应受轨道不平顺影响显著，改善线路条件能有效提高列车的乘车舒适性.拖车随机响应与动车类似，文中未给出计算结果.

图8 中跨跨中桥梁竖向位移随机响应Fig.8 Random response of vertical displacement of middle span midpoint

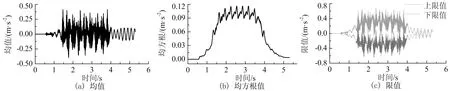
图9 中跨跨中桥梁竖向加速度随机响应Fig.9 Random response of vertical acceleration of middle span midpoint

图11和图12分别给出了中跨跨中桥梁和动车车体竖向加速度功率谱.从图11可以看出，由列车重力荷载引起的确定性响应功率谱的主要频率小于7 Hz，而轨道不平顺引起的随机性功率谱主要分布在25～40 Hz之间.总体来说，列车重力对桥梁竖向振动起主要作用，但7 Hz以上的高频振动还主要是由轨道不平顺引起的.

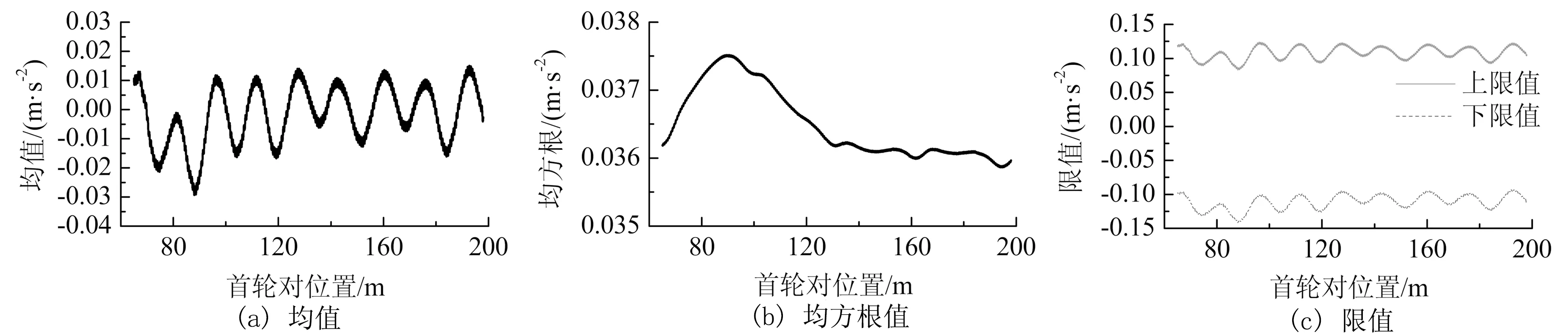
图10 动车车体竖向加速度随机响应Fig.10 Random response of vertical acceleration of trailer car body

频率/Hz (a) 确定性响应

频率/Hz (b) 随机性响应图11 中跨桥梁跨中竖向加速度功率谱Fig.11 PSD of vertical acceleration of bridge middle span midpoint

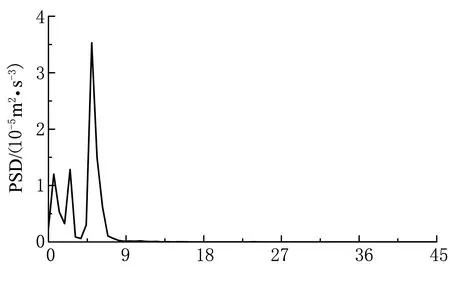
频率/Hz (a) 确定性响应

频率/Hz (b) 随机性响应图12 动车车体竖向加速度功率谱Fig.12 PSD of vertical acceleration of locomotive car body

从图12可以看出，动车车体竖向加速度的确定性功率谱和随机性功率谱均主要分布在0～9 Hz的低频范围，这是由于车辆悬挂系统的减振作用，高频轮轨振动被大大削弱.另外，车体随机响应功率谱随列车运行时间波动并不显著，说明下部桥梁变形对车体振动影响不大，车体振动是一个近乎平稳的随机过程.

4．2 车速影响分析

为研究车-桥耦合系统随机响应随车速的变化规律，结合线路实际运营情况，本文选取了9种不同的车速开展车-桥随机振动分析，其中车速从200 km/h～400 km/h，按25 km/h递增.表6给出了不同车速下车辆和桥梁随机响应最大值.从表中可以看出：

表6 不同车速下车辆和桥梁竖向随机响应最大值Tab.6 Maximum value of random response of train and bridge under different speeds

1)桥梁和车辆随机动力响应的均方根随车速的增大而增加，表明车速越高，由轨道不平顺引起的耦合系统振动响应离散度越大，以往根据单样本计算的车-桥耦合振动响应的误差越大.

2)不同车速下，桥梁跨中竖向随机振动位移最大值为0.85 mm，满足我国《铁路桥涵设计基本规范》(TB 10002.199)中关于预应力混凝土简支梁跨中竖向挠度小于L/800的规定.跨中桥梁竖向随机振动加速度最大值为0.98m/s2，满足我国《高速铁路设计规范》中关于无砟轨道桥梁桥面竖向振动加速度小于5 m/s2的规定.动车和拖车车体竖向随机振动加速度最大值分别为0.168 m/s2和0.202 m/s2，满足我国《高速铁路设计规范》中关于桥上列车车体竖向振动加速度半峰值小于1.3 m/s2的要求.同时，不同车速下耦合系统振动响应的最大值远低于规范要求，表明我国现有高速铁路线路简支桥梁安全富余度较大，线路平顺等级较高.

5 结 论

通过建立基于IIM和虚拟激励法的列车-轨道-桥梁耦合系统竖向随机振动分析模型，开展了高速铁路列车-简支梁桥竖向随机振动研究，主要得到如下结论：

1)改进的车-桥耦合迭代计算模型在保持与传统模型相同精度计算结果的前提下，能使计算效率提高5倍左右.

2)在车-桥耦合系统中，轨道结构的弹性作用对桥梁和车辆动力响应具有显著影响，建立合理的列车-轨道-桥梁耦合系统模型能更加准确地计算车辆及桥梁系统的动力响应.

3)由于轨道随机不平顺的激励作用，采用基于虚拟激励法的车-桥耦合系统随机振动分析模型能更加精确和高效地开展车-桥随机振动分析.

4)高速铁路简支梁桥竖向位移主要受列车自重控制，轨道不平顺对其影响很小；桥梁和车辆竖向加速度受轨道不平顺影响显著，改善线路条件能有效提高列车的乘车舒适性；同时，车速越高，桥梁和车辆随机响应的均方根越大，由轨道不平顺引起的耦合系统振动响应离散度越大.

[1] 张志超,张亚辉,林家浩.基于虚拟激励法的车桥系统车速影响分析[J].铁道学报,2011,33(4):93-99.

ZHANG Zhi-chao, ZHANG Ya-hui, LIN Jia-hao. Influence of train speeds on random vibration of trainbridge systems[J]. Journal of the China Railway Society, 2011,33(4):93-99.(In Chinese)

[2] 王贵春,潘家英.轨道不平顺导致的车桥耦合振动分析[J].铁道工程学报，2006,23(8): 30-33，57.

WANG Gui-chun, PAN Jia-ying. Analysis of vehiclebridge coupled vibration due to track irregularities[J]. Journal of Railway Engineering Society，2006,23(8): 30-33，57. (In Chinese)

[3] 夏禾,张楠.车辆与结构动力相互作用[M].北京:科学出版社,2005:105-106,313-319.

XIA He, ZHANG Nan. Dynamic interaction of vehicles and structures[M]. Beijing: Science Press,2005:105-106,313-319. (In Chinese)

[4] LV F, LIN J H, KENNEDY D,etal. An algorithm to study non-stationary random vibrations of vehicle-bridge systems[J]. Computers and Structures,2009,87(3):177-185.

[5] 林家浩,张亚辉.随机振动的虚拟激励法[M].北京:科学出版社,2004:42-58.

LIN Jia-hao, ZHANG Ya-hui. Pseudo excitation method in random vibration[M]. Beijing: Science Press,2004:42-58. (In Chinese)

[6] ZHANG Z C, ZHANG Y H, LIN J H,etal. Random vibration of a train traversing a bridge subjected to traveling seismic waves[J]. Engineering Structures, 2011, 33(12): 3546-3558.

[7] 朱艳,李小珍.车桥时变耦合系统的随机响应分析[J].武汉理工大学学报,2010,32(9):352-355;

ZHU Yan, LI Xiao-zhen. Stochastic dynamic responses analysis of train-bridge timevarying system[J]. Journal of Wuhan University of Technology,2010,32(9):352-355. (In Chinese)

[8] LOU P, YU Z W, AU F T K. Rail-bridge coupling element of unequal lengths for analyzingtrain-track-bridge interaction systems[J]. Applied Mathematical Modelling, 2012,36(4):1395-1414.

[9] 朱志辉, 朱玉龙, 余志武,等. 96m钢箱系杆拱桥动力响应及行车安全性分析[J]. 中国铁道科学, 2013,34(6):21-29.

ZHU Zhi-hui, ZHU Yu-long, YU Zhi-wu,etal. Analysis on the dynamic response and running safety of 96 m steel box tied arch bridge[J]. China Railway Science,2013,34(6):21-29. (In Chinese)

[10]吴定俊,李奇,陈艾荣.车桥耦合振动迭代求解数值稳定性问题[J].力学季刊,2007,28(3):405-411.

WU Ding-jun, LI Qi, CHEN Ai-rong. Numerical stability of iteration scheme for solution of vehiclebridge coupling vibration[J]. Chinese Quarterly of Mechanics, 2007, 28(3): 405-411. (In Chinese)

[11]杜宪亭,夏禾,张田.车桥耦合振动迭代求解稳定性研究[J].振动与冲击,2012,31(22):62-65.

DU Xian-ting, XIA He, ZHANG Tian. Numerical stability of iterative scheme in solving coupled vibration of a train-bridge system[J]. Journal of Vibration and Shock, 2012,31(22):62-65. (In Chinese)

[12]ZHANG N, XIA H. Dynamic analysis of coupled vehicle-bridge system based on inter-system iteration method[J]. Computers & Structures, 2013, 114(1): 26-34.

[13]杜宪亭,夏禾,张田,等. 基于精细Runge-Kutta混合积分法的车桥耦合振动非迭代求解算法[J]. 振动与冲击,2013,13:39-42，55.

DU Xian-ting, XIA He, ZHANG Tian,etal. Non-iterative solving algorithm for coupled vibration of a train-bridge system based on precise Runge-Kutta hybrid integration method[J]. Journal of Vibration and Shock,2013,13:39-42，55. (In Chinese)

[14]全顺喜.高速道岔几何不平顺动力分析及其控制方法研究[D].成都:西南交通大学土木工程学院,2012:49-50.

QUAN Shun-xi. Study on dynamic analysis and control methods of the geometric irregularity in high-speed turnout[D]. Chengdu: School of Civil Engineering, Southwest Jiaotong University, 2012:49-50. (In Chinese)

[15]周毅.CRTSⅢ型板式轨道减振特性研究[D].成都:西南交通大学土木工程学院,2011: 14-16.

ZHOU Yi. Research on vibration-reduction performance of CRTSⅢ slab ballastless track[D]. Chengdu: School of Civil Engineering, Southwest Jiaotong University, 2011: 14-16. (In Chinese)

[16]朱志辉,余志武,朱玉龙,等. 车桥振动诱发周围环境及建筑物振动分析[J].铁道学报,2013,35(4):102-109.

ZHU Zhi-hui, YU Zhi-wu, ZHU Yu-long,etal. Analysis on environment and building vibration induced by passing trains on bridge structures[J]. Journal of the China Railway Society,2013,35(4):102-109. (In Chinese)

[17]程潜.考虑列车纵向相互作用的高架车站动力分析[D].北京:北京交通大学土木工程学院,2013:50-51.

CHENG Qian. Dynamic analysis of elevated station considering vehicle longitudinal effects[D].Beijing: School of Civil Engineering, Beijing Jiaotong University,2013:50-51. (In Chinese)

[18]范俊杰.现代铁路轨道[M].第2版．北京:中国铁道出版社,2004:67.

FAN Jun-jie. Modern railway track[M].2nd ed.Beijing: China Railway Publishing House,2004:67. (In Chinese)

Study on Vertical Random Vibration of Train-bridge Coupled System Based on Improved Iteration Model

ZHU Zhi-hui1,2†, WANG Li-dong1, GONG Wei1, YU Zhi-wu1,2, CAI Cheng-biao3

(1. School of Civil Engineering, Central South Univ, Changsha, Hunan 410075, China；2. National Engineering Laboratory for High Speed Railway Construction, Central South Univ, Changsha, Hunan 410075, China；3. State Key Laboratory of Traction Power, Southwest Jiaotong Univ, Chengdu, Sichuan 610031, China)

By using the improved iteration model for train-bridge coupled system, the analysis model of train-track bridge vertical random vibration based on Pseudo Excitation Method (PEM) was established. PEM was applied to transform the random track irregularities into the superposition of a series of vertical harmonic irregularities, while the iteration calculation was applied to solve the equation of the train-bridge coupled system. Taking a five-span simply-supported beam bridge passed through by a CRH2 high-speed train as numerical example, the accuracy and efficiency of the improved iteration model for train-bridge coupled system was verified. The results show that the calculation efficiency of the improved model is about 5 times that of the conventional model under the same calculation accuracy. The mean value and the root mean square (RMS) of the vertical random vibration response for train-track-simply supported beam bridge, which are caused by deterministic load and track irregularities, respectively, were calculated. It can be seen that the vertical displacement of the bridge is mainly controlled by the weight of the train, but the excitation of track irregularity has little effect on it. The vertical acceleration of the bridge and car bodies are significantly influenced by track irregularities, and the improvement of the track condition can effectively improve the riding comfort. The RMS of the train-bridge coupled system random vibration and the discrete of the vibration caused by track irregularities increase with the acceleration of train speed.

train-bridge coupled vibration; iteration model; Hertz contact; pseudo excitation method; simply supported beam bridge

1674-2974(2016)11-0120-11

2015-12-13

国家自然科学基金资助项目(51378511, 51678576), National Natural Science Foundation of China(51378511, 51678576); 牵引动力国家重点实验室开放课题(TPL1601)

朱志辉(1979-)，男，河南潢川人，中南大学副教授，工学博士†通讯联系人，E-mail:zzhh0703@163.com

U213

A