多级三角形格栅加筋板的力学性能

范华林,江 舒

(河海大学力学与材料学院,江苏 南京 210098)



多级三角形格栅加筋板的力学性能

范华林,江 舒

(河海大学力学与材料学院,江苏 南京 210098)

为了研究碳纤维格栅结构的力学性能,设计一种多级格栅加筋板结构,并采用理论分析和有限元计算等方法对该结构的力学性能进行分析。将格栅结构等效为均质连续结构,推导了格栅结构的等效计算方法,计算多级格栅加筋结构的等效弹性模量及等效弯曲刚度。结果表明,多级三角形格栅加筋结构的存在将大大提高超轻质材料的抗屈曲能力;当截面面积相同时,三角形格栅的弯曲刚度比实体结构提高10%,表明多级格栅比普通格栅具有更高的屈曲荷载。

多级结构;格栅加筋板;三角形格栅;力学性能;等效弹性模量

图1 格栅加筋板壳结构形式Fig. 1 Grid-stiffened plate and shell structures

点阵结构是一种有序的多孔结构,胞元呈周期性排列、胞元杆系为拉伸主导型构型的一类结构,具有很强的断裂韧性[1-3]。范华林等[4-6]研究发现,通过改进胞元壁结构特征,引入多级结构,将复合材料以不同尺度的结构基元通过多种相互作用搭建,可以有效提高材料的比刚度和比强度,进一步提高材料的抗屈曲性能和断裂韧性,突出了材料的高韧性特征。Kim[7]制备的格栅加筋筒结构在端部采用了法兰加强结构(图1)使结构各部分受力更加均匀。研究发现,相比于纯粹的网格结构,柱壳加筋结构可更有效的增加结构的整体刚度,有利于提高结构的质量效率。

在二维点阵结构中,三角形格栅在宏观应力作用下是拉伸主导型结构,具有较强的承压和抗弯能力,并且三角形格栅是最稳定的,可以作为承力结构单独使用[8-9]。三角形格栅加筋板壳结构是目前格栅材料在工程领域中的最主要结构形式[8]。隋倩倩等[10]提出多级三角形格栅夹芯板结构为典型的双侧蒙皮格栅结构。轻质点阵结构材料作为一种新型的轻质多功能复合材料,在航空航天等领域有着广泛的发展前景[11-13],但是对于格栅加筋板的等效计算理论还不完善,因此对于多级格栅加筋板结构力学性能的计算是非常有意义的。本文提出了单侧蒙皮三角形格栅结构,分析其面内外弹性本构关系,由杆件的轴向力和变形间的线性关系转换得到等效连续介质计算模型。计算加筋板的等效弹性模量和弯曲刚度,将其与传统格栅板进行对比,并对其承载力进行分析。

1 多级格栅基本结构

设计了一种新型格栅板,如图2所示。传统格栅结构为矩形截面,而该格栅结构为T形截面,具体尺寸见图3。图3中:t1、t2分别为T形截面上部宽度和下部宽度;b1、b2分别为T形截面上部高度和下部高度;w为矩形截面宽;h为矩形截面高。

图2 T形截面格栅加筋板结构形式Fig. 2 Grid-stiffened plate with T-type cross-section

2 多级格栅板的理论分析

Hohe等[14-15]提出了一种能量等效方法。假设典型体单元中所有单元变形能与宏观等效均质尺度上单元的变形能相等,计算等效应变、应力和应变能。根据每个方向上杆件的轴向力和变形与等效均质单元应力应变的转换关系,由杆件的轴向力和变形间的线性转换关系得到等效连续介质计算模型。点阵格栅单元是由多组不同方向的基本杆件单元组成的周期结构,单元长度一般在厘米量级以下,远小于工程结构尺寸,因此可将点阵材料视作均匀连续介质,用连续介质力学的方法求解点阵材料的力学参数。

图3 T形截面尺寸及等效为矩形截面的尺寸Fig. 3 Sizes of T-type cross-section and equivalent rectangular cross-section

2.1 面内弹性本构关系

(1)

式中:ρ*——点阵材料整体密度;ρs——胞壁母体材料密度;t——壁厚;l——三角形的边长。胞壁沿x3向的厚度用b表示,此处取单位厚度,即b=1。三角形格栅受x2方向的单向应力σ22作用,如图4所示。图4中，1,2,3为杆件编号;Δh为高度在x2方向的增量;Δli为杆i的增量。令Ni为第i组杆件中的内力(i=1,2,3),则单胞的平衡方程可写为

(2)

各杆内力为

(3)

考虑点阵单胞的变形模式,如图4(c)所示,在变形后的构型基础上可建立如下几何关系：

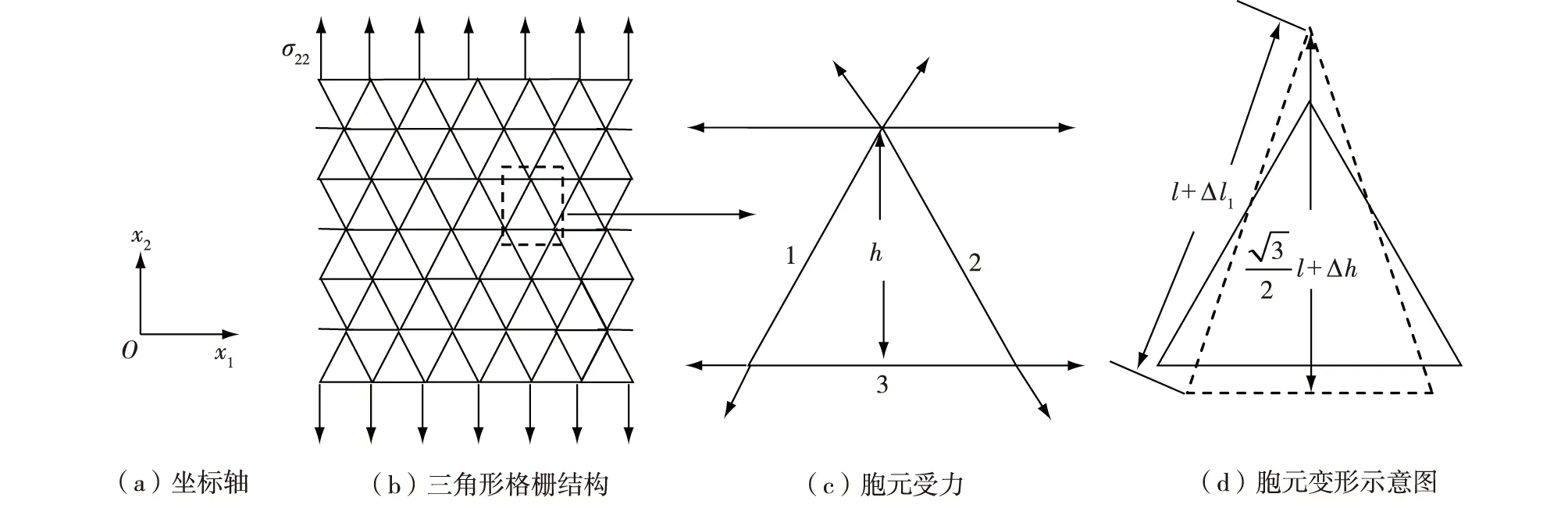
图4 三角形格栅结构的平面受力及变形示意图Fig. 4 Sketch of plane stress and deformation of triangular grid structure

(4)

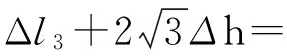
(5)

式中:F——杆件所受外力;L——杆长;E——弹性模量;A——截面积;Es——材料的弹性模量。单胞有效应变和变形量之间的关系为

(6)

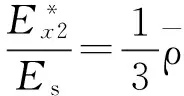
(7)

(8)

式中:E*——均质结构弹性模量;w*——等效结构宽度。

2.2 面外弹性本构关系

假设格栅加筋板等效前后的弯曲刚度和拉伸刚度不变,将格栅结构视为连续的层合板结构,如图5所示。加筋板等效为中间等效结构时(图5(a)、图5(b)),上、下两部分截面高度和弹性模量不变,中间结构等效为均质结构时,总高度,宽度,抗弯刚度和抗拉刚度不变(图5(b)、图5(c))。根据复合材料层合板计算公式,结构的拉伸刚度计算表达式为

(9)

其中,z方向即为x3方向。则弯曲刚度D的计算表达式为

(10)

式中:υ——泊松比;E(z)——层合板的弹性模量。根据平行移轴定理,截面惯性矩I为

(11)

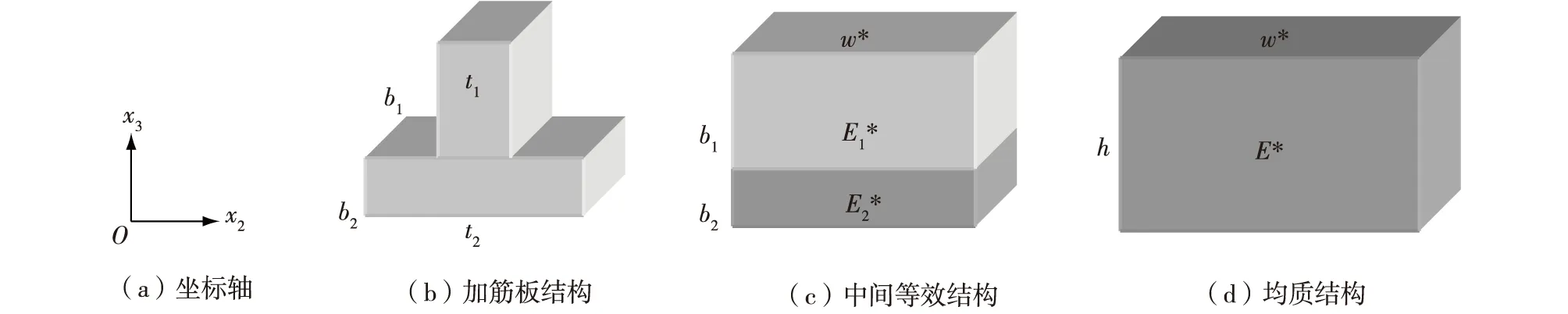
图5 格栅夹芯板结构的等效形式Fig. 5 Equivalent structure of grid-stiffened structure

如果将层合板结构等效为均质板,则其参考面可由下式确定

(12)

(13)

其中

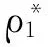
T形截面的面积为:A梯=t1b1+t2b2,矩形截面的面积为:A矩=h*w,其中,b1+b2=h*。

(14)

根据格栅加筋板与均质层合板的弯曲刚度和拉伸刚度相等,可得

(15)

式中:I1——T形截面上部的惯性矩;I2——T形截面下部的惯性矩;I——矩形截面的惯性矩。I1、I2可由下式求出

(16)

式中：yc——T形截面形心坐标值。代入上式可以解得

(17)

根据等效前后界面的拉伸刚度和弯曲刚度相等,可以解得

(18)

2.3 与传统格栅结构的弯曲刚度对比

传统格栅结构为矩形截面,宽度为w,高度为h,则矩形截面三角形格栅(边长为l)结构的弯曲刚度为

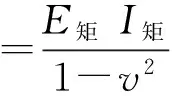
(19)

由式(7)可得

(20)

根据惯性矩公式,可得

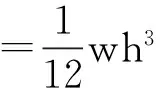
(21)

(22)

分别绘制出矩形和T形截面的弯曲刚度D随着三角形格栅长细比变化的图像,如图6所示。当T形截面和矩形截面面积相同时,T形截面的弯曲刚度明显比矩形截面的弯曲刚度大,因此,多级格栅加筋板的抗屈曲能力高于传统格栅板10%。

3 多级格栅承载能力分析

3.1 强度破坏理论

在截面积相同的条件下,当材料强度控制结构破坏时,多级格栅具有与普通格栅相同的极限承载能力。

3.2 整体屈曲理论

图6 T形截面与矩形截面的弯曲刚度Fig. 6 Bending stiffness of T-type and rectangular cross-sections

图7 三角形格栅的两种屈曲模态Fig. 7 Two buckling modes of triangular grid

4 结 语

本文将多级三角形格栅结构等效为均质板结构,采用两种理论进行等效计算。理论一为面内等效理论,将两层均质板采用叠加原理进行等效叠加,求得等效弹性模量。理论二为面外等效理论,通过等效前后弯曲刚度和拉伸刚度不变,得到等效均质板的厚度与等效模量的计算公式。

通过与传统格栅结构进行对比,多级格栅加筋板的刚度相对于传统格栅板有了明显的提高,即多级格栅加筋板在一定程度上将提高材料的抗屈曲能力,具有更高的弯曲刚度,即具有更好的抗弯和抗屈曲性能,体现出多级格栅加筋板的优越性。

[1] VASILIEV V V, BARYNIN V A, RASIN A F. Anisogrid lattice structures survey of development and application[J]. Composite Structures, 2001, 54(2/3): 361-370.

[2] KIM T D. Fabrication and testing of composite isogrid stiffened cylinder[J]. Composite Structures 1999,45 (1): 1-6.

[3] KIDANE S. Buckling analysis of grid stiffened composite structures[D]. Ababa:Addis Ababa University, 1997.

[4] 范华林,孟凡颢,杨卫.碳纤维格栅结构力学性能研究[J].工程力学,2007,24(5):42-46. (FAN Hualin, MENG Haofan,YANG Wei. Structural mechanics of lattice grids reinforced by carbon fibers [J]. Engineering Mechanics, 2007, 24(5):42-46.(in Chinese))

[5] FAN H L, FANG D N. Enhancement of mechanical properties of hollow strut foams: analysis[J]. Materials & Design, 2009, 30(5): 1659-1666.

[6] FAN H L, JIN F N, FANG D N. Mechanical properties of hierarchical cellular materials: Part I. analysis[J]. Composites Science and Technology, 2008, 68(15-16):3380-3387.

[7] KIM T D. Fabrication and testing of composite isogrid stiffened cylinder[J]. Composite Structures, 1999,45 (1): 1-6.

[8] ABRATE S. Continuum modeling of latticed structures: Part I [J]. Shock and Vibration Digest, 1985, 17(1): 15-21.

[9] LAI C L, WANG J B, LIU C. Parameterized finite element modeling and buckling analysis of six typical composite grid cylindrical shells[J]. Applied Composite Materials, 2014, 12: 739-758.

[10] 隋倩倩,江舒,孙方方,等.多级三角形格栅夹芯板力学分析[J].复合材料学报,2016,33(3): 675-680.(SUI Qianqian, JIANG Shu,SUN Fangfang,et al. Mechanical analysis of hierarchical isogrid sandwich plate[J]. Acta Materiae Compositae Sinica, 2016,33(3): 675-680.(in Chinese))

[11] RALPH E L, LINDER E B. Advanced solar panel designs advanced solar panel designs[C]//Piscataway.Conference Record of the IEEE Photovoltaic Specialists Conference. NJ:IEEE Press, 1996:297-300.

[12] MOROZOV E V, LOPATIN A V, NESTEROV V A.Finite-element modeling and buckling analysis of anisogrid composite lattice cylindrical shells[J].Composite Structures, 2011, 93: 308-323.

[13] KIM T D. Fabrication and testing of composite isogrid stiffened cylinder[J]. Composite Structure, 1999,45:1-6.

[14] HOHE J, BECKER W. Effective elastic properties of triangular grid structures[J]. Composite Structures, 1999, 45(2): 131-145.

[15] HOHE J, BESCHORNER C, BECKER W. Effective elastic properties of hexagonal and quadrilateral grid structures [J]. Composite Structures, 1999, 46(1): 73-89.

[16] WANG A J, MCDOWELL D L. In-plane stiffness and yield strength of periodic metal honeycombs [J]. ASME Journal of Engineering Materials and Technology, 2004, 126:137-156.

[17] 章继峰, 张博明, 杜善义.平板型复合材料格栅结构的增强改进与参数设计[J].复合材料学报,2006,23(3): 153-157(ZHANG Jifeng,ZHANG Boming,DU Shanyi.Im provement and parameter design of advanced composite grid plate structures [J]. Acta Materiae Compositae Sinica,2006,23(3):153-157.(in Chinese))

[18] FAN H, JIN F, FANG D. Uniaxial local buckling strength of periodic lattice composites[J]. Materials & Design, 2009, 30(10): 4136-4145.

Mechanical properties of multilevel triangular grid-stiffened plate

FAN Hualin, JIANG Shu

(CollegeofMechanicsandMaterials,HohaiUniversity,Nanjing210098,China)

In order to study mechanical properties of a carbon fiber grid structure, a type of multilevel grid-stiffened plate was designed, and its mechanical properties were analyzed using theoretical analysis and the finite element method. The grid structure was equivalent to a homogeneous continuous structure. Based on this, an equivalent method for calculation of the grid structure was derived, and the equivalent elastic modulus and the equivalent flexural stiffness of a multilevel grid-stiffened structure were calculated. The results show that the multilevel triangular grid-stiffened structure can improve the anti-buckling ability of ultra-light materials. When the cross-sectional area is the same, the flexural stiffness of the triangular grid is 10% higher than that of the solid structure, indicating that the buckling load of the multilevel grid is higher than that of an ordinary grid.

multilevel structure; grid-stiffened plate; triangular grid; mechanical property; equivalent elastic modulus

10.3876/j.issn.1000-1980.2016.06.005

2016-01-26

国家自然科学基金(11172089,11372095)

范华林(1974—),男,四川富顺人,教授,博士,主要从事复合材料力学研究。E-mail:fhl02@mails.tsinghua.edu.cn

O341

A

1000-1980(2016)06-0498-06