基于多因素分析的配网线损改进方法研究

李德祥，吕驰，陈薇冰，付家志，程乐峰，李石东，胡锡，李正佳

（1. 广西电网有限责任公司南宁供电局，广西 南宁，530032；2. 苏州华天国科电力科技有限公司，江苏 苏州 215000）

基于多因素分析的配网线损改进方法研究

李德祥1，吕驰1，陈薇冰1，付家志1，程乐峰2，李石东2，胡锡2，李正佳2

（1. 广西电网有限责任公司南宁供电局，广西 南宁，530032；2. 苏州华天国科电力科技有限公司，江苏 苏州 215000）

对于配网线损计算，在传统算法中应用较多的是均方根电流法，它一般用于三相供电较平衡、负荷变化平缓、日负荷曲线峰谷差较小的情况。但由于目前配电网的自动化水平较低，数据采集系统存在一定误差，导致按照传统线损计算方法得到的结果会产生较大偏差。因此，通过对多种线损影响因素进行分析，引入电网规划建设因素、电网技术因素、运行管理因素，提出了一种基于多因素分析的配网线损改进方法，并根据实际数据对算法进行了验证。结果表明配网线损改进方法的计算结果精度更高，更加符合实际情况，有利于准确分析配网线损来源，合理使用降损措施，提高电网运行的经济性。

配电网；多因素分析；改进算法；线损；电网规划

0 引言

线损计算是电网众多计算技术中的重要一部分，计算所得的线损率直接反映了电网的损耗大小和运行效率，是评价电网公司的一项重要经济技术指标，对电网部门的线损管理和评估起到重要指导作用，并对电网的实际规划具有指导意义。线损的大小整体上体现了电网的设计、运行以及相关部门管理维护水平的高低。所以，线损率的准确计算、预测是减少供电成本、提高电网运行效率的重要环节。

目前，在10kv配网系统中，线损计算应用较为基础是均方根电流法[1，2]。并在此算法基础上，发展出了等值电阻法、平均电流法和最大电流法等计算方法[3]。但这些方法对电网拓扑结构的基本原始参数要求很高，在电网实际计算中，使用这些方法往往需要花费大量的人力、物力、财力，因此实施难度很大。回路电流法[4]能结合实际监控终端数据，是电网计算中较为理想的计算方法。但因实际配网系统自动化水平较低、测量数据存在一定误差等原因，使得回路电流法计算所得的线损与实际线损误差较大，不明损耗明显，影响了电网公司的综合管理，不利于评估配电网结构及其运行方式的经济性。回归分析法[5，6]在电网中也有相当广泛的应用，但回归方程的确定需丰富的个人经验，不利于在不同的电网结构中广泛使用。另外，随着人工神经网络的发展，为配电网线损计算提供了新思路[7-14]，神经网络算法无需输入和输出数学表达式，仅通过样本的训练就能实现从输入到输出的函数映射。但计算过程过于复杂，不利于大规模电网线损计算的实施。分群算法[8]将样本数据分类，再利用BP型神经网络映射到每个群的样本数据，利用这种算法计算配网线损精度高，误差小，但计算速度过慢且计算过程复杂，无法结合到实际电网的线损计算中。

以上电网配网线损计算方法并没有系统全面的考虑实际运行中的各项影响因素，对实际电网中的应用意义不大，缺少可操作性，很难对电网中配网线损计算提出实质性帮助[9-12]。综合考虑以上情况，本文将建立精确、全面、符合实际的配网线损计算模型。

本文主要通过对电力网线损理论计算进行分析，在满足计算要求的精度下，将影响电网线损因素进行分类，考虑主要因素，忽略次要因素，并对主要因素进行量化，建立相应数学模型，利用数学模型对电网技术线损计算分析。最终结合南宁供电局算例，进一步缩小管理因素线损，分析不明线损，达到配网线损合理化、透明化的目的。

1 线损影响因素分析

在配电网中，线损的大小受到多方面因素影响，按照各因素性质主要可以分为四类：规划建设因素、技术因素、管理因素和外在因素[15]。

规划建设因素主要分为四大类：即电网设备配置、电 压等级的确定、电网布局、设备的选型等。在传统电网设计中，虽然已经较全面地考虑了以上因素，但很少考虑因自然因素、人为因素等导致的设备老化[16]而带来的额外损耗。因此，本文着重分析设备老化对配网线损的影响。

管理因素指电网的实际运行方式、三相不平衡度、供电设备的维护和健康情况，以及所采取的抄表方式、用户违章用电和窃电损失、电网元件漏电与故障损失、营业中抄表核收差错损失等。三相负荷不平衡是在配电网中普遍存在的一个问题，可以通过提高管理方式等来有效改善三相不平衡的情况，对此，本文根据配网实际情况着重分析三相不平衡度和线损之 间的关系。

电网技术因素指通过技术手段改变线损大小的方式，主要包括：调压、调频、调容技术、无功补偿技术、电网规划设计安装技术等。其中，调压和无功补偿是电网中较常用、成本较低的技术，由于无功补偿也可以改善电网的电压水平，所以本文主要对配网中电压合格率进行评估，并考虑其对配网线损的量化影响。

外在因素指当地气象条件、实际负荷特性等不属于上述三者因素、不受人为影响的一些客观变量，此类因素在电网运行过程中很难通过人为因素来改进，或者改进的成本太高，因此暂不考虑外在因素对线损计算的影响。

1.1 设备老化影响

在配电网线损中，变压器和线路的损耗占绝大部分，其中变压器的老化对其损耗的影响更大，因此在设备老化问题中，主要选取变压器作为研究对象。在1954 年，美国通用电气对设备寿命的评估问题[17]提出了一种理论，其基本思想是基于“预知维护”的一种评估模式，通过各种有效手段对运行中的电力设备做出健康程度的诊断和预测，并根据结果对电力设备的寿命进行合理评估，同时还可以有针对性地进行检修。在1996 年，该公司再次提出了基于电力变压器的诊断技术的寿命预测模型。对于预知维护和评估技术，它们的核心思想都是基于电力设备中各元件的健康水平状况，并由此对未来的运行状况做出科学性预测。此类评估思想对于设备安全稳定运行的意义是极具参考价值的[18，19]。但是，无可置否，此类评估思想的重点始终集中于设备自身，其明显缺点是无法考虑到设备的运行环境和影响设备运行的其他因素。作为一种设备运行寿命的评估方法，它缺少全面性、综合性。本文在现有研究的基础上，除了考虑影响变压器运行的内在和外在因素之外，并主要分析变压器的老化对线损的影响。

在变压器老化所增加的线损中，损耗主要包括两个部分[20]：

1）变压器的固定损耗会随着变压器的老化而逐渐增加，并随着变压器泄漏电流的增大而增大；

2）变压器的可变损耗与流经变压器的电流及变压器自身等效内阻有关，随着变压器的老化，其自身等效内阻逐渐增大，导致变压器损耗增加。

本文在建立变压器老化影响模型中，考虑了EA公司的健康评估计算模型，该模型的核心是在设备老化原理的基础上，评估设备健康水平与运行时间的变化关系，该模型广泛应用于北美和英国电力设备的健康状态预测。

健康水平指数计算公式[21]：

式中，HI0为变压器的健康水平指数的初值 ，HI 是经过一段时间运行后变压器的健康水平指数 ，B 为老化系数，T1是全新变压器HI0对应的年份，一般为该变压器投运年份，T2是与所要计算的 HI 对应的年份，可为当前年份，也可为未来年份。

文献[21]指出健康水平指数的评估范围为 0-10，其值越低等效于变压器状态越好。健康水平指数处于 0-3 之间代表变压 器运行状态良好，且变压器性能稳定、故障发生概率处于较低的水平，变压器的健康水平指数和故障发生概率在评估有效时间内不会有太大的波动和起伏；健康水平指数处在 3-6.5 之间代表变压器已经出现一定程度上的老化现象，并且老化过程开始上升，虽然这时变压器的故障发生概率依旧处于较低水平，但已开始进入上升阶段，老化率也开始逐步上升；当健康水平指数大于 6.5 时，代表变压器已经出现严重的老化，处于这种状态下，故障发生概率显著上升，所对应的老化速率也会出现明显上升趋势。

1.2 三相电流不平衡度影响

在电力系统中，当三相负荷不平衡时，各相负荷电流不相等，则等价于在相间产生不平衡电流，最终不平衡电流流过中性线，将会增加中性线负荷。当三相负荷不平衡电流在极端情况下时，线路线损会增加5倍，而在配网中三相不平衡问题比较突出，因此分析配网线损中三相不平衡度对线损计算十分重要。为便于研究三相不平衡与损耗变化的关系，现引入负荷电流不平衡度并考虑三相负荷电流不平衡时线损的增加率[22-24]。

根据南宁市电网中给出的不平衡度数据定义，不平衡度k为三相中最大相电流与最小相电流的差值与该线路额定电流的比值，即

其中，k为三相不平衡度，Imax为最大相电流，Imin为最小相电流，IN为线路额定电流。

假定三相四线制线路的单位长度相线电阻为R，单位长度中性线电阻为2R（一般中性线截面为相线截面的一半）。

则三相不平衡时相线功率损耗P为：

其中，P为三相总功率损耗，ka、kb、kc分别为A、B、C相不平衡率，I为平均电流。

中性线上电流为：

其中，I0为中性线电流，Iav、Ibv、Icv分别为A、B、C各相平均电流，则中性线损耗为：

其中，P0为中性线损耗。

1.3 电压合格率影响

目前，中压电网电压调控手段偏少，在负荷高峰或者低谷时受限于设备自动化水平。负荷分布、配电网结构等条件限制，很多地区只能依靠人工改变电压分接头或者粗犷式无功补偿来调节电压，因此造成在电网中电压合格率严重偏低，很大程度上造成不必要的线路损失[25，26]。因此，将电压合格率考虑到线损计算及降损分析中具有合理、切合实际的作用。

电压合格率，即为在一定时间内，在规定范围值之下的电压与超出规定范围值电压的比值。传统的电压合格率定义为：在电压限定范围之内，监测点实际运行电压累计运行时间和系统总运行时间的比值。其定义表达式如下：

空巢老人缺乏情感慰藉，常伴孤独、焦虑、抑郁等负面情绪，持久、反复体验后，易转为一种长期的精神刺激，直接影响心理健康状态。宋洁等人研究表明，空巢老人情绪低落易诱发免疫功能异常，亦会导致或加重抑郁症状[10]。因此，排解空巢老人生活中的不良情绪，有助于提高其心理健康水平。

其中，Uhg（%）为电压合格率，Tyx为电压越限累计运行时间，Ttotal为监测点电压运行时间。

考虑到电压合格率对配网线损的影响，本文引进一个电压影响系数，对原有计算线损进行修正：

其中，Ku为电压影响系数。

2 基于多因素分析的线损改进算法

在传统线损计算方法中，均方根电流法应用的最为广泛。在主网和高压配电网中，由于电压等级高，管理规范，三相不平衡、电压合格率以及其他技术、管理、规划因素对线损的影响较少，且测量精度高，利用传统均方根电流法能够较准确的反映出线损的实际情况。而在低压配网中，三相不平衡、电压合格率等问题较突出，同时低压线路、变压器等设备众多，管理难度大，导致按照传统线损计算方法无法准确反映出实际损耗，因此需要对现有的线损计算方法进行改进，使其具有更高的应用性，有利于电网管理部门分析和管理线损。

基于多因素分析的线损改进算法是结合传统配网线损计算并将设备老化、三相电流不平衡度、电压合格率等影响因素进行综合考虑的改进算法。结合前文所述，将影响线损的四种因素：规划建设因素、技术因素、管理因素和外在因素分别选取各大因素中的主要影响因子建立数学模型，进而计算出各因素权重模型，在传统均方根电流法基础上，综合考虑各因素影响结果，最后得出基于多因素分析的线损改进算法。

在传统线损计算方法[27-29]中，计算线损分为变压器线损和线路线损两部分，线路线损计算公式为：

其中，R0为线路等效电阻，Ki为第i条线路负荷形状系数，Pi为第i条线路输入供电量，Uav为线路平均电压，cosФav为线路平均电压，T为测量周期，Ai为线路供电量。

其中，Pki为第i个变压器额定功率，INi为第i个变压器额定电流，ii（t）为第i个变压器输入电流，Pi（t）为第i个变压器输入电量，Ui（t）为第i个变压器额定电压。

在此基础上，进一步考虑前文提及的影响因素。对于设备老化，根据健康水平指数公式，可以得到老化系数B：

其中，HI=6.5、HI0=0.5、T2-T1=50（选取变压器额定工作年限为50年），计算得B=0.0051。

对于三相电流不平衡度，根据变压器和线路的不同进行分开考虑，假设三相四线制配网中一相负荷重载，一相轻载，一相正常，则有：

其中，k为总三相不平衡度，ka、kb、kc分别为A、B、C相不平衡率。结合上式得三相四线制10kV输电线线损为：

其中，Px为三相四线制10kV输电线线损。对于变压器损耗，同样基于线路一相重载，一相轻载，一相正常的情况，并且不存在中性线的影响，则三相不平衡率略小于线路损耗，其表达式为：

其中，Pb为三相不平衡情况下，变压器损耗。对于电压合格率，则将最终线损乘以前文所定义的电压影响影响系数。综上多因素分析的配网改进算法的线损计算方式为：

其中，ΔAl为未考虑三相不平衡下的线路损耗，ΔAT为未考虑三相不平衡下的变压器损耗，ΔT为变压器实际运行年数。

基于多因素分析的线损算法流程如图1。

3 算例分析

以南宁市10kv配网为例，选取南宁市2015年全年数据。根据均方根电流法，在传统配网线损计算中，依据式（8）、（9）计算，以九月份南宁市兴宁区安波929线路数据为例：其中R0为查询对应线路型号，利用等效电阻法求得0.55Ω/km，馈线总长3km；cosφav为0.94；电压等级选取10kV；周期为一个月720小时；形状系数Ki为1.5；该线路九月输入电量Ai为2103720瓦，计算损耗为252849.799度。此为安波929线路九月线损总和。在变压器损耗中根据变压器型号计算：取安波929线路一号公变，其型号为SCB11-800/10.5，额定功率800kW；空载损耗170kW；负载率0.48；功率因素0.97；电压等级10kV；计算得损耗80度。将南宁市10kV线路损耗与变压器损耗进行统计得九月份总线损为4036万度。图2为传统均方根线损算法结果与南宁局测量数据对比。

图1 基于多因素分析的线损算法流程图Fig.1 Flowchart of line loss algorithm based on multiple factor analysis

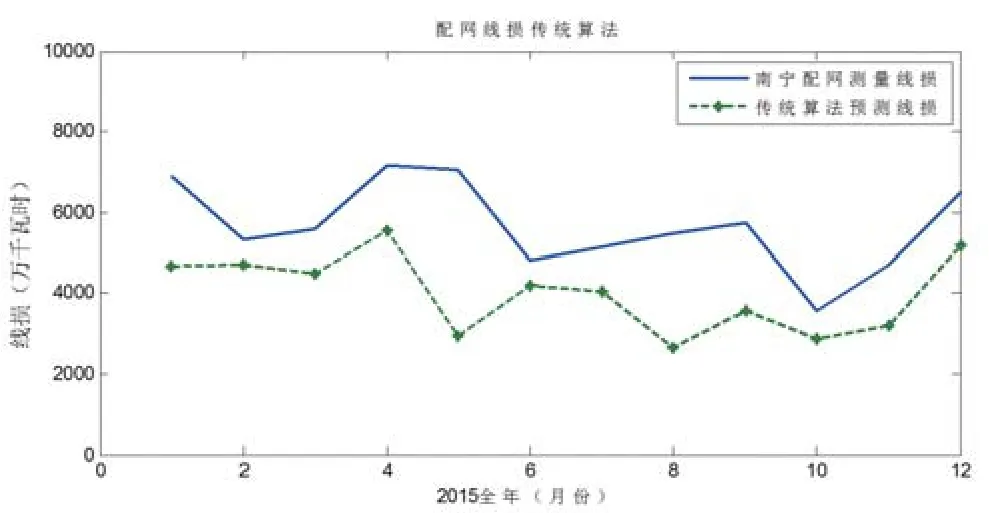
图2 2015南宁市10kV配网测量损耗与传统方均跟值电流法计算结果对比Fig.2 Results comparison between the measuring loss of Nanning 10kV distribution network in 2015 and the conventional RMS current method

从图2可看出，传统的配网计算方法计算出的线损变化趋势与实际测量结果近似相符，反映了传统均方根算法一定的合理性，因此以均方根电流法为基础，同时结合多因素分析进行改进也是比较合理的。但是从计算线损量的绝对值上来看，传统算法计算所得量明显小于测量值，月计算误差在5%～30%之间，平均在11%左右，可见在利用传统均方根法进行配网线损计算的时候，误差较大。通过分析可以得知，在传统的线损计算中，特别是主网计算中，三项不平衡、电压合格率等多方面因素的影响较小，加上管理严格，测量装置齐全，精度较高，因此传统的均方根电流算法并没有考虑多方面技术、管理因素的影响。而在实际配网中，考虑到三相不平衡、电压不合格等问题普遍存在，且影响较大，同时线损管理难度大，就会导致按照传统均方根算法计算出的线损值会明显小于实际测量值。所以在配网线损计算中，传统均方根算法对于不明线损的分析较为乏力，不利于电网公司的经济性管理和规划。

根据本文提出的改进配网线损计算方法，在原有的4036万度损耗基础上，考虑多方面影响因素，根据式（14）进行计算，其中Ku为1.159；Δ T取6.68年，得老化系数为1.033；三相不平衡率为0.18；则调整后结果为4948.05906万度。下图3为利用改进算法计算得到的结果，可以发现，相比较传统的均方根电流算法，改进算法得到的结果与实际测量值更加接近，在线损变化趋势基本一致的基础上，相对误差也明显减少。同时由于考虑了设备老化、三相不平衡度等多种因素，并建立了相应计算模型，使得供电单位能够对电网线损的组成进行准确计算，分析各部分因素对线损的影响大小，以便于通过合理、经济的手段来有效降低损耗。

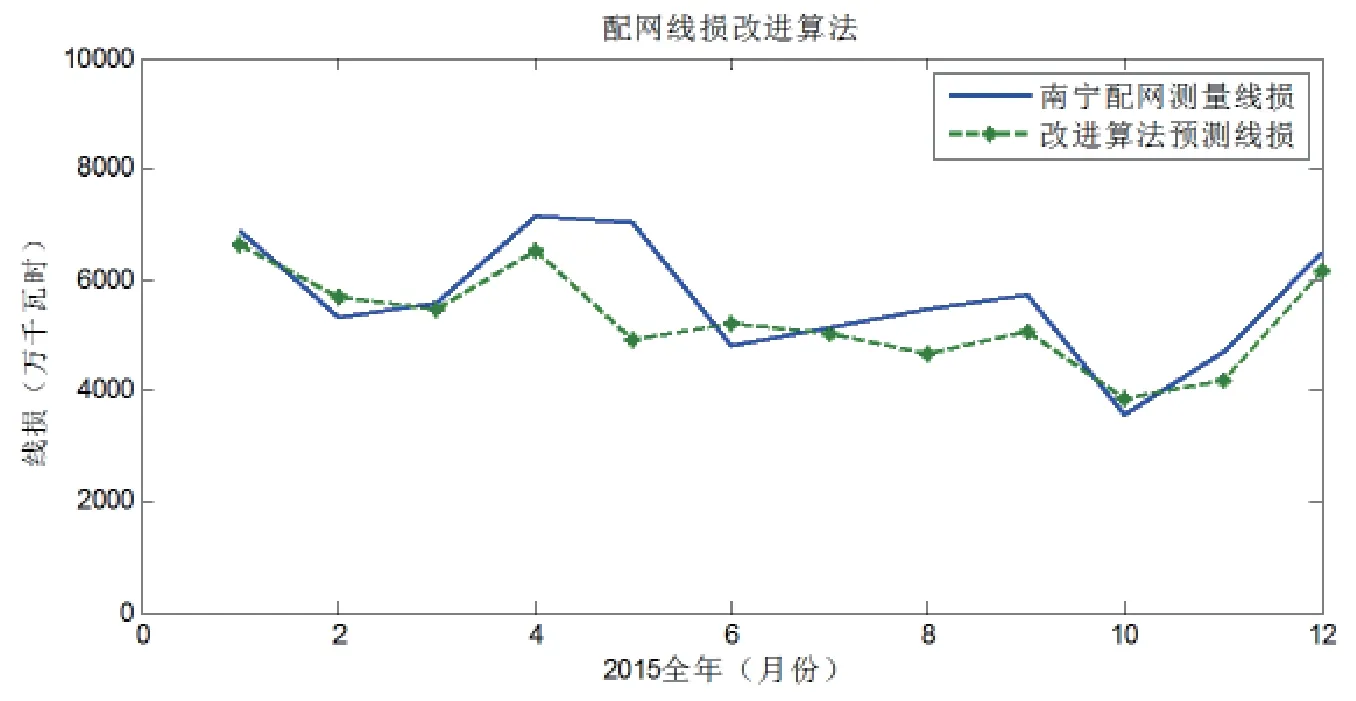
图3 2015南宁市10kV配网测量损耗与改进线损算法结果对比Fig.3 Results comparison between the measuring loss of Nanning 10kV distribution network in 2015 and the improved line loss algorithm

4 总结

本文通过分析配网中线损计算中传统均方根电流法的不足，提出一种基于多因素分析的配网改进线损算法。该算法从实际出发，将设备老化、三相电流不平衡、供电电压三类主要因素加入传统计算模型，实现了对南宁电网线损的合理计算和分析。根据多因素改进算法模型，能有效预测各类因素对实际线损的影响，有利于供电单位对各类降损手段的科学规划，有效提高经济性。

在实际应用中，根据改进算法模型，可以分解出各因素单独对线损的影响，从而使得供电公司能够针对性地采取相应的降损措施，避免盲目地进行各类改造工程。同时也能够对降损工程的投入产出进行量化、分析，使得降损效果能够最大化，这样不但可以提高降损工程的经济性，也最大程度上减少线损，提高电网运行的经济性。另外，尽管基于多因素分析的线损改进算法要求的测量数据要比传统线损算法多，但是大部分数据如三相不平衡度、电压合格率等已经实现计量，能够从供电公司的计量系统直接读取，因此并不会增加太多工作量，而且改进算法模型使用较简便，使得改进算法拥有较高的适应性和易操作性。

[1] 扈国维. 配电网线损计算与降损技术措施研究[D]. 华北电力大学（北京），2015.

G W Hu. The research of distribution network line loss calculation and the measure for reducing loss[D]. North China Electric Power University（Beijing），2015.

[2] 冉兵，宋晓辉. 配电网线损影响因素分析[J]. 华中电力，2009，22（6）：30-33.

B Ran，X H Song. Analysis on Influencing Factors of Distribution Network Line Loss[J]. Central China Electric Power，2009，22（6）：30-33.

[3] 白帆. 等值电阻法计算线损的简化研究[D]. 河北大学，2014.

F Bai. Study on The equivalent resistance method to simplify the calculation of line loss[D]. Hebei University，2014.

[4] 王刚军，王承民，李恒，等．基于实测数据的配网理论网损计算方法[J]．电网技术，2002，26（12）：18-20.

G J Wang，C M Wang，H Li Heng，et al. Calculation method of theoretical network loss in power distribution network based on measured data[J]. Power System Technology，2002，26（12）：18-20.

[5] 王新炜．井冈山茨坪城区电网规划及配电自动化建设研究[D]．华北电力大学，2015.

X W Wang. Research of power grid planning and the construction of distribution automation in Jinggangshan Ciping town[D] . North China Electric Power University，2015.

[6] 何川，蒋晓艳. 基于一元线性回归模型的农村用电量预测[J]. 西藏科技，2013，20 （10）：74-76.

C He，X Y Jiang. Forecast of rural electricity consumption based on variate linear regression model[J]. Xizang Technology，2013，20（10）：74-76.

[7] S W Kau，M Y Cho，C Z Chen，et al．Distribution feeder loss analysis by using an artificial neural network[J]. Electric Power Systems Research，1995，34（2）：85-90.

[8] 文福拴，韩祯祥．基于分群算法和人工神经元网络的配电网线损计算[J]．中国电机工程学报，1993，13（3）：41-50.

F S Wen，Z X Han. The calculati on of energy losses in distribution systems based upon a clustering algorithm and an artificial neural network model[J]. Proceedings of the CSEE，2002，1993，13（3）：41-50.

[9] 唐晓勇．配电网线损计算方法研究[D]．湖南大学，2014.

X Y Tang. Research on line loss calculation method of distribution network [D]. Hunan University，2014.

[10] 韩永强，季小慧. 基于IGA-BP综合算法的人工神经网络在线损计算中的应用[J]. 中国电力教育，2011，27（9）：101-103.

Y Q Han，X H Ji. Application of artificial neural network in line loss calculation based on IGA-BP [J]. China Electric Power Education，2011，27（9）：101-103.

[11] 姜惠兰，安敏，刘晓津，等．基于动态聚类算法径向基函数网络的配电网线损计算[J]．中国电机工程学报，2005，25（10）：35-39 .

H L Jiang，M An，X J Liu，et al. The calculation of energy losses in distribution systems based on RBF network with dynamic clustering algorithm[J]，Proceedings of the CSEE，2005，25（10）：35-39.

[12] 李亚，刘丽平，李柏青，等．基于改进 K-Means 聚类和 BP 神经网络的台区线损率计算方法．中国电机工程学报，2016，36（17）：4543-4550.

Y Li，L P Liu，B Q Li，et al. Calculation of line loss rate in transformer district based on improved K-Means clustering algorithm and BP neural network[J]. Proceedings of the CSEE，2016，36（17）：4543-4550.

[13] 郝庆辉. 基于RBF神经网络的配电网线损计算与分析[D]．东北石油大学，2014 .

Q H Hao. Calculation and analysis of power distribution network line loss on RBF neural network[D]，Northeast Petroleum University，2014.

[14] 饶尧，邱泽晶，彭旭东. 基于层次分析法的电网能效影响因子分析研究[J]. 节能技术，2014，32（1）：51-54.

Y Rao，Z J Qiu，X D Peng. Analysis of grid energy efficiency factors based on analytic hierarchy process[J]，Energy Conservation Technology，2014，32（1）：51-54.

[15] 饶锐，程乐峰，宋浩佳，等. 基于多频超声波原理的变压器故障检测方法探究[J]. 新型工业化，2015，5（7）：57-63.

R Rao，L F Cheng，H J Song，et al. Research on transformer fault detection method based on the principle of multi-frequency ultrasonic waves[J]，The Journal of New Industrialization，2015，5（7）：57-63.

[16] 刘有为，马麟，吴立远，等. 电力变压器经济寿命模型及应用实例[J]. 电网技术，2012，36（10）：235-240.

Y W Liu，L Ma，L Y Wu，et al. Economic life model of power transformer and its application[J]，Power System Technology，2012，36（10）：235-240.

[17] T Nakagawa. Sequential imperfect preventive maintenance policies [J]，IEEE Transactions on Reliability，1988 ，37（3）：295-298.

[18] 高亚娴. 电力变压器故障诊断及寿命预测方法的研究[D]. 西安电子科技大学，2007.

Y X Gao. A study of fault diagnosis and life expectancy for transformer [D]，Xidian University，2007.

[19] 王慧芳，赵婉芳，杜振东，等. 基于寿命数据的电力变压器经济寿命预测[J]. 电网技术，2015，39（3）：810-816.

H F Wang，W F Zhao，Z D Du，et al. Economic life prediction of power transformers based on the lifetime data [J]，Power System Technology，2015，39（3）：810-816.

[20] 潘艳蓉. 配电网线损考核指标及降损策略的研究[D]. 武汉大学，2004.

Y R Pan. Study on the check index for line losses and strategy to reduce line losses in distribution grid [D]. Wuhan University，2004.

[21] 梁博渊，刘伟，杨欣桐. 变压器健康状况评估与剩余寿命预测[J]. 电网与清洁能源，2010，26（11）：37-43.

B Y Liang，W Liu，X T Yang. Transformer condition assessment and residual life prediction [J]，Power System and Clean Energy，2010，26（11）：37-43.

[22] 曾惜，肖敏. 三相负荷不平衡对线损的影响[J]. 贵州电力技术，2016，19（3）：82-84.

X Zeng，M Xiao. The influence of three-phase unbalanced load on line loss[J]，Guizhou Electric Power Technology，2016，19（3）：82-84.

[23] 牛迎水，崔素媛. 低压三相电流不平衡对线损的影响与治理[C]. 电能质量及柔性输电技术研讨会，2014：409-414.

Y S Niu，S Y Cui. Impacts and control of low-voltage three-phase current unbalance on linw loss [C]，Power Quality and Flexible Transmission Technology Seminar，2014：409-414.

[24] 冯成，徐长宝，李怀宇，等. 三相电流不平衡及谐波对电网损耗的影响分析[J]. 电气应用，2016，35（13）：47-52.

C Feng，C B Xu，H Y Li，et al. Impact analysis of three-phase current unbalance and harmonic on power grid loss [J]，Electrotechnical Application，2016，35（13）：47-52.

[25] 张先泰，蔡金锭，丁智华，等. 电容补偿在配电网电压调节中的应用[J]. 电力自动化设备，2011，31（2）：116-118+128.

X T Zhang，J D Cai，Z H Ding，et al. Application of capacitance compensation in voltage adjustment of distribution power system [J]，Electric Power Automation Equipment，2011，31（2）：116-118+128.

[26] 郑霓虹. 配电网无功优化方法的研究[D]. 重庆大学，2002.

N H Zheng. Research on reactive power optimization of the radial distribution system [D]，Chongqing University，2002.

[27] 张祥华. 10kV配电网极限线损计算方法研究[D]. 华南理工大学，2014.

X H Zhang. Calculation method research about ultimate line losses of 10 kV distribution network [D]. South China University of Technology，2014.

[28] 苏志雄，曾民星，孔灿，等. 基于线损影响因素的配电网线损计算方法研究[J]. 电气应用，2013，S1：413-416.

Z X Su，M X Zeng，C Kong，et al. Research on distribution network line loss calculation method based on line loss impact factors [J]，HElectrotechnical Application，2013，S1：413-416.

[29] 温建春，韩学山，张利. 一种配电网理论线损计算的改进算法[J]. 电力系统及其自动化学报，2008，20（4）：72-76.

J C Wen，X S Han，L Zhang. Improved method for theoretical line loss calculation of distribution network [J]，Proceedings of the CSU-EPSA，2008，20（4）：72-76.

[30] 程乐峰，陈艺璇，余涛. 配网变压器节能改造技术和方法探讨[J]. 新型工业化，2016，6（6）：23-38.

L F Cheng，Y X Chen，T Yu. Discussion on energy conservation and reconstruction techniques and methods of distribution transformers [J]，The Journal of New Industrialization，2016，6（6）：23-38.

[31] 徐志，程乐峰，余涛，郭成，郑炜楠. 基于Android平台的电力节能诊断计算器APP设计与应用[J]. 广东电力，2015，28（11）：116-120.

Z Xu，L F Cheng，T Yu，et al. Development and Application of a power energy conservation and diagnosis calculator based on Android platform [J]，Guangdong Electric Power，2015，28（11）：116-120.

Study on Improved Loss Calculation Method for Distribution Network Based on Multiple Factor Analysis

LI De-xiang1, LV Chi1, CHEN Wei-bing1, FU Jia-zhi1, CHENG Le-feng2, LI Shi-dong2, HU Xi2, LI Zheng-jia2
(1. Nanning Power Supply Bureau, Guangxi Power Grid Co., Ltd., Nanning 530032, China; 2. Suzhou Huatian Power Technology Co., Ltd., Suzhou 215000, China)

Root-mean-square (RMS) current method is widely used in loss calculation of distribution network. It’s applicable to the situation of balanced three-phase power and small change in load. But because of the low automation level, there still exists a certain amount of err ors in data collection system, which leads to the large errors in the results of loss calculation. Thus, the paper came up with an improved loss calculation method based on multiple factors, including power network planning factors, technical factors and management factors. By the calculation case with actual data, the result showed that the improved method was more accurate than the traditional RMS current method, and can help to analyze loss composition more precisely, take reduction measures more reasonably and enhance economy of power network.

Distribution network; Multiple factors analysis; Improved algorithm; Line loss; Power system planning

李德祥，吕驰，陈薇冰，等. 基于多因素分析的配网线损改进方法研究[J]. 新型工业化，2016，6（10）：20-28.

10.19335/j.cnki.2095-6649.2016.10.004

: LI De-xiang, LV Chi, CHEN Wei-bing, et al. Study on Improved Loss Calculation Method for Distribution Network Based on Multiple Factor Analysis[J]. The Journal of New Industrialization, 2016, 6(10)： 20-28.

中国南方电网科技项目资助(040100 [2016] 030200JH00090)

李德祥（1986-）男，通信作者，工程师，本科，从事节能、线损等工作；吕驰（1974-），男，电力工程师，本科，从事电力规划及节能环保工作；陈薇冰（1978-），女，工程师，硕士，从事节能、线损工作，对管理降损方面有较深研究；付家志（1986-），男，电气工程师，本科，从事管理线损方面；程乐峰（1990-），男，博士研究生，主要研究方向为配网自动化、电力系统优化运行与控制等；李石东（1995-），男，湖南岳阳，研究生，从事电能质量与节能方向；胡锡（1991-），男，研究生，从事电能质量与节能方向；李正佳（1972-），男，高级工程师，硕士，主要从事电力通信、电力系统行业等研究工作