考虑轨道约束的重载铁路大跨度连续刚构桥地震响应
2016-12-16涂鹏周文涛闫斌
涂鹏,周文涛,闫斌,2
(1.中南大学 土木工程学院,湖南 长沙 410075;2.高速铁路建造技术国家工程实验室,湖南 长沙 410075)
考虑轨道约束的重载铁路大跨度连续刚构桥地震响应
涂鹏1,周文涛1,闫斌1,2
(1.中南大学 土木工程学院,湖南 长沙 410075;2.高速铁路建造技术国家工程实验室,湖南 长沙 410075)
为研究大跨度重载铁路连续刚构桥与轨道系统地震响应规律,建立考虑轨道约束的重载铁路大跨度连续刚构桥与轨道系统一体化仿真模型。以某6-32 m简支梁+(108+180+108) m重载铁路连续刚构桥+6-32 m简支梁为例,分析轨道约束和相邻桥跨对自振特性的影响,研究一致激励下梁轨系统地震响应,探讨路基段长度、线路纵向阻力和地形对系统地震响应的影响,研究地震与温度的耦合作用机理。研究表明:轨道约束和相邻桥跨会使自振频率增大;系统地震响应与地震频谱特性有关;考虑相邻桥跨后,钢轨最大地震应力、墩顶水平力最大值和墩顶水平位移均有所增大;随着路基段长度的增大,钢轨地震应力最大值增大,墩底水平力最大值和墩顶水平位移减小,路基段长度建议至少取100 m;铺设无砟轨道时的钢轨地震应力最大值大于有砟轨道和小阻力扣件,其墩顶水平力和墩顶水平位移三者最小。随着桥墩高度的增大,墩顶水平力增大;地震与温度荷载耦合作用时的钢轨应力不等于两者单独作用时结果的线性叠加。
重载铁路;轨道约束;相邻桥跨;连续刚构桥;梁轨相互作用;地震响应
重载铁路以运量大、低成本、高效率为特点,可加强地区的货物运输,是今后铁路货运的重点发展方向[1]。近些年来,在我国发展迅速,已相继修建了山西晋煤-渤海湾铁路、朔黄铁路、瓦日线铁路等一系列重载铁路。大跨度连续刚构桥具有刚度大,变形小的优点,在重载铁路中的应用日益广泛,但因为梁墩刚接,所以连续刚构桥-轨道系统对下部结构变形极为敏感。近年来,地震频发,研究考虑轨道约束的重载铁路大跨度连续刚构桥地震响应规律是十分有必要的。
国内外学者关于重载铁路梁轨相互作用课题进行了一定研究,YANG[2]研究了重载铁路线路检修;戴公连等[3]研究了不同小阻力扣件布置方案对重载铁路连续梁桥上无缝线路的受力特性;殷明旻等[4-5]研究了30t和40t轴重重载铁路无缝线路纵向力分布规律;张永亮等[6]采用反应谱法及弹塑性时程反应分析法对一实桥进行了地震反应分析及抗震性能评价。但是,关于大跨度重载铁路连续刚构桥与轨道系统地震响应研究相当匮乏,地震作用下的系统受力特性仍不明确。
本文采用非线性杆单元来模拟线路纵向阻力,用竖向刚臂模拟梁高,用线性弹簧模拟扣件竖向刚度[7-9],以某6-32 m简支梁+(108+180+108) m连续刚构桥+6-32 m简支梁为例,建立了考虑轨道约束的重载铁路大跨度连续刚构桥与轨道系统一体化仿真模型,分析了轨道约束和相邻桥跨对自振特性的影响,研究了一致激励下梁轨系统地震响应,探讨了路基段长度、线路纵向阻力和地形对系统地震响应的影响,研究了地震与温度的耦合作用机理。

1 考虑相邻桥跨的连续刚构桥-轨道系统仿真模型
文中(108+180+108) m连续刚构桥采用单箱单室箱型截面,箱梁采用C60混凝土,桥面宽度为12 m,跨中梁高7.5 m,支点梁高13.5 m(截面见图1(a))。
32 m简支梁截面形式如图1(b)所示,由四片T梁组成。桥面宽度为9.1 m,梁高2.6 m。

(a)连续刚构桥截面;(b)重载铁路32 m简支梁截面示意图单位:cm图1 桥梁截面Fig.1 Section
本文中的桥梁场地属于“V型峡谷”,7号-10号桥墩为连续刚构桥桥墩,7号和10号桥墩高60 m,8号和9号桥墩高80 m。桥墩采用矩形薄壁墩,墩体采用C40混凝土,墩壁内侧布置直径22 mm的HRB335钢筋,采用纤维梁单元来模拟桥墩混凝土采用Kent-Park模型,钢筋采用Menegotto-Pinto模型,桥墩截面弯矩-曲率特性如图2(a)所示。
1号-6号和11号-16号桥墩为简支梁桥墩,1号-6号桥墩高度分别为6,15,24,33,42和51 m,11号-16号桥墩高度与1号-6号对称。简支梁桥墩采用圆形薄壁墩,墩壁内侧布置布置直径22 mm的HRB335钢筋,采用纤维梁单元来模拟桥墩混凝土采用Kent-Park模型,钢筋采用Menegotto-Pinto模型,桥墩截面弯矩-曲率特性如图2(b)所示。

(a)连续刚构桥桥墩弯矩-曲率曲线;(b)简支梁桥墩弯矩-曲率曲线图2 桥墩弯矩-曲率曲线Fig.2 Moment-curvature curve of pier
采用带刚臂的梁单元模拟梁体,梁墩刚接,墩底固结。
桥上铺设双线有砟轨道,钢轨为75 kg/m轨[10]。二期恒载180 kN/m。在桥台两侧各建立200 m路基上的钢轨[11]。简支梁的支座布置顺序都是左固右活,固定支座采用线性弹簧模拟,活动支座采用非线性弹簧模拟,摩擦系数取0.03,开始滑动的临界位移为3.0 mm。
有砟轨道线路纵向阻力r与梁轨相对位移u的关系可表示为式(1)[6]:
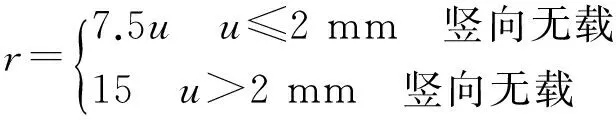
(1)
系统采用Rayleigh阻尼,阻尼比h为0.05,阻尼系数α和β按下式(2)取值:
(2)
式中:w1和w2为第一阶和对结构纵向振型贡献最大的一阶频率。
桥梁场地属于Ⅱ类场地,抗震设防烈度为8度。在进行地震荷载作用分析时,地震波选用1 940,Elcentro Site,270Deg波(PGA=0.356 9 g)、1 952, Taft Lincoln School, 69 Deg波(PGA=-0.155 7 g)和1 971, San Fernando, 69 Deg波(PGA=0.315 4 g),保留各地震波的频谱特性,仅将地震最大峰值加速度调整为0.3 g(设计地震)[12],地震波持续时间取30 s,地震反应谱如图3所示。
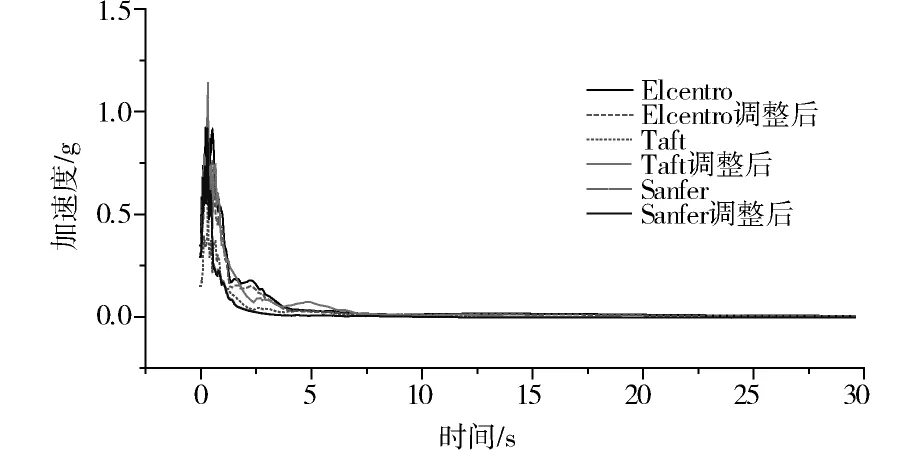
图3 地震反应谱Fig.3 Earthquake response spectrum
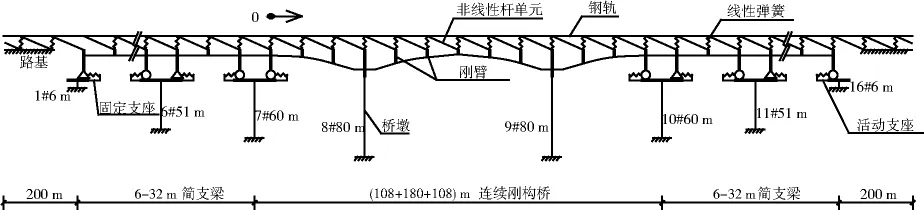
图4 重载大跨度连续刚构桥-轨道相互作用模型Fig.4 Simulation model for large span continuous rigid frame bridges and track system under heavy haul railway
2 重载大跨度连续刚构桥-轨道系统动力特性
2.1 轨道约束的影响
分别计算考虑轨道约束和不考虑轨道约束时的自振特性[13-14],并提取前10阶进行对比分析,结果见表1。
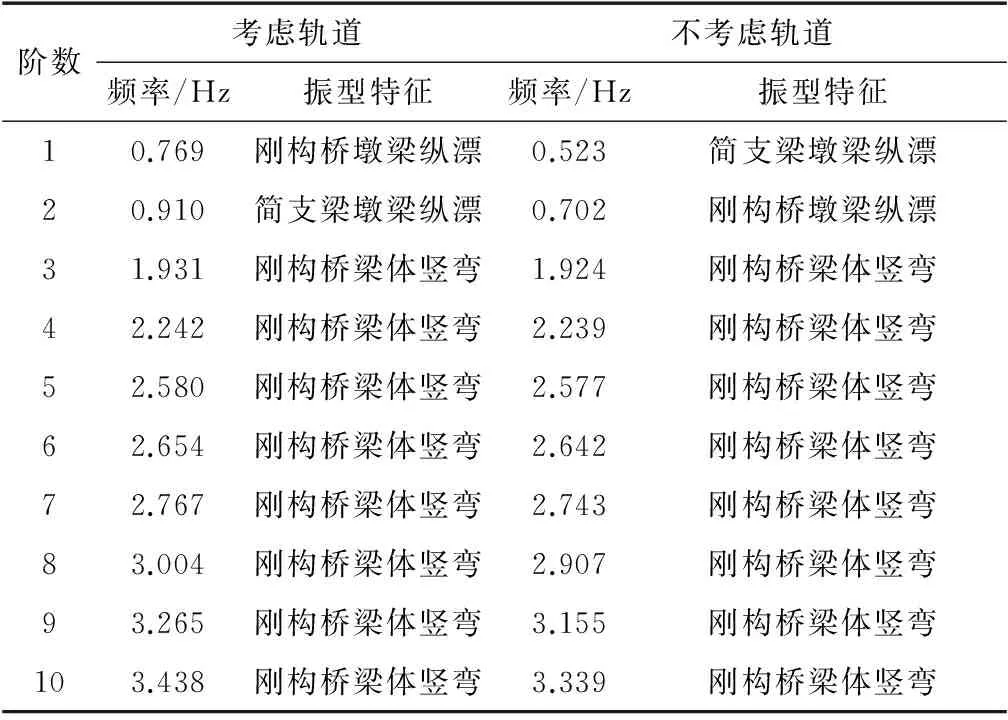
表1 轨道对自振特性的影响
由表1可知,考虑轨道约束作用时,轨道结构增强了桥梁的顺桥向约束,系统整体性得到增强,前两阶自振频率大幅增大,增幅达47.0%,后8阶系统自振频率两者几乎一致。因此,在计算系统自振特性的时候,需要考虑轨道带来的纵向约束影响。
2.2 相邻桥跨的影响
在考虑轨道约束的条件下,分别计算考虑简支梁和不考虑简支梁时的自振特性,并提取前10阶进行对比分析,结果见表2。
表2 相邻桥跨对自振特性的影响
Table 2 Influence of adjacent bridge span on self-vibration characteristics
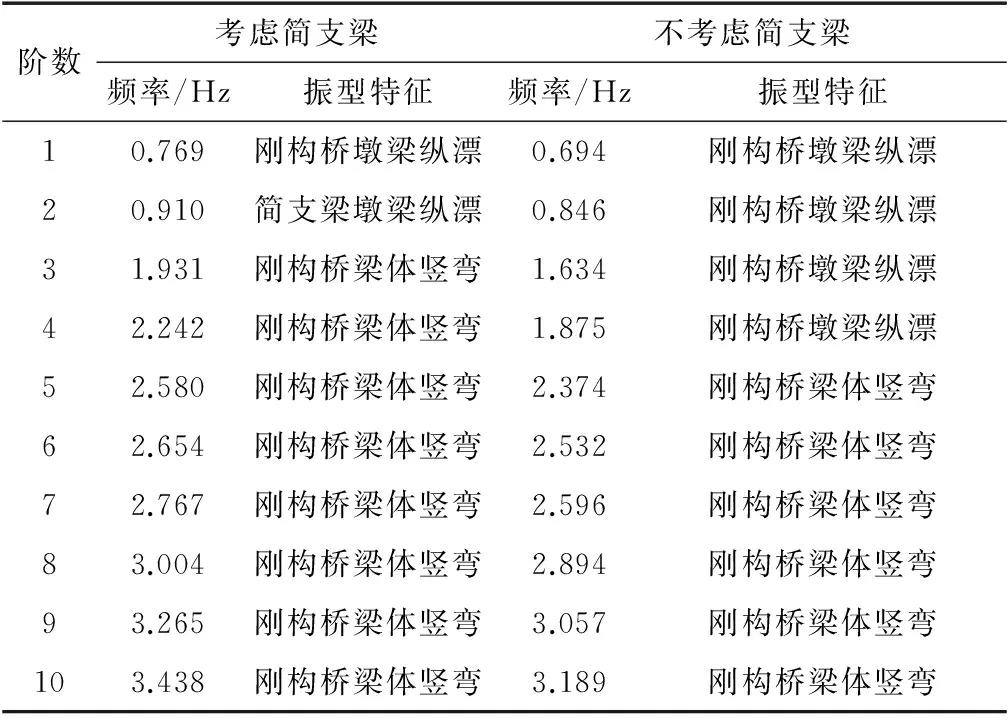
阶数考虑简支梁不考虑简支梁频率/Hz振型特征频率/Hz振型特征10.769刚构桥墩梁纵漂0.694刚构桥墩梁纵漂20.910简支梁墩梁纵漂0.846刚构桥墩梁纵漂31.931刚构桥梁体竖弯1.634刚构桥墩梁纵漂42.242刚构桥梁体竖弯1.875刚构桥墩梁纵漂52.580刚构桥梁体竖弯2.374刚构桥梁体竖弯62.654刚构桥梁体竖弯2.532刚构桥梁体竖弯72.767刚构桥梁体竖弯2.596刚构桥梁体竖弯83.004刚构桥梁体竖弯2.894刚构桥梁体竖弯93.265刚构桥梁体竖弯3.057刚构桥梁体竖弯103.438刚构桥梁体竖弯3.189刚构桥梁体竖弯
由表2可知,考虑简支梁时,系统前10阶自振频率均有增大,最大增幅达18.0%。考虑简支梁时,系统刚度和质量发生改变,顺桥向约束增强,各制动墩承受的桥梁质量增大,地震响应增强,系统自振频率有所增大。
3 重载大跨度连续刚构桥-轨道系统地震响应
3.1 系统地震响应规律
在进行地震响应分析时,地震激励选用Elcentro波、Taft波和Sanfer波,计算一致激励下的钢轨和桥墩(9号)受力和水平位移,计算结果见图5。
由图5可知,梁轨系统地震响应与地震频谱特性有关。最大钢轨地震应力发生在连续刚构桥与简支梁相连处,Elcentro波的最大钢轨应力大于Taft波和Sanfer波,为168.0 MPa(压)和171.0 MPa(拉)。地震作用下,最大墩顶水平力都是位于9号桥墩处,Elcentro波的最大墩顶水平力大于Taft波和Sanfer波,为6 697.3 kN。因为7号桥墩处布置了两个活动支座,所以其墩顶水平力迅速减小。最大墩顶水平位移均发生在9号桥墩处,Elcentro波作用时,为186.3 mm。
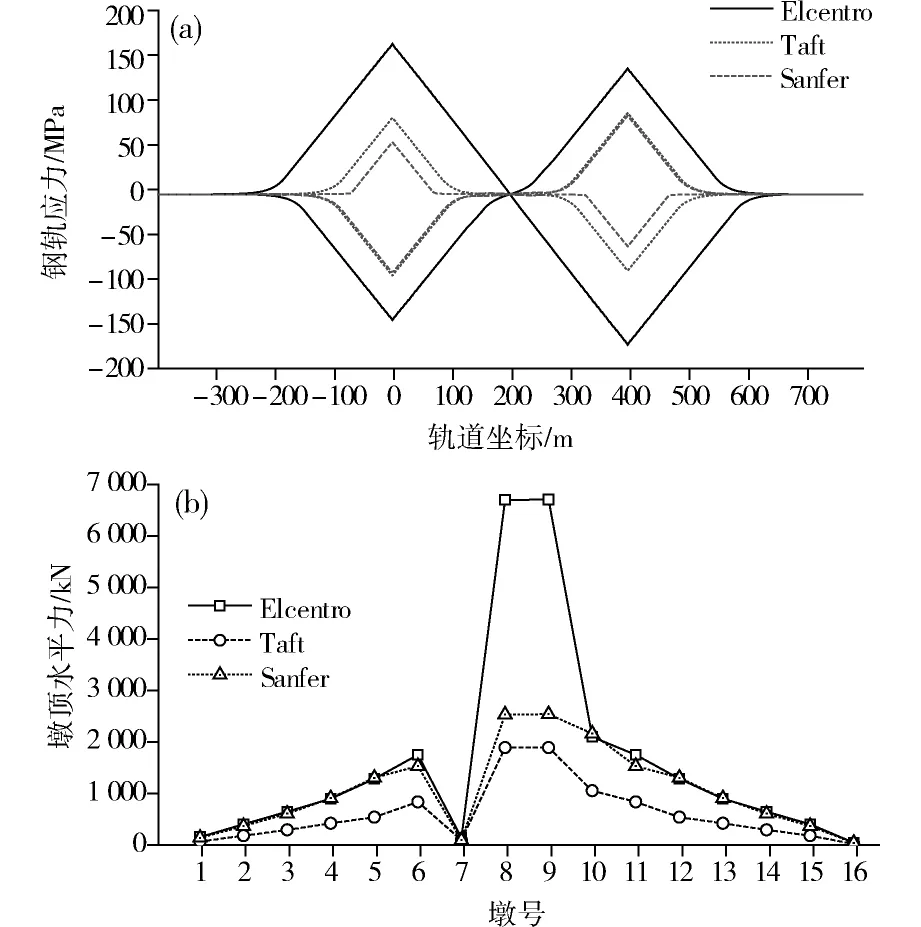
(a)钢轨地震应力包络;(b)墩顶水平力最大值图5 系统地震响应Fig.5 Seismic response of system
3.2 相邻桥跨对系统地震响应的影响
为研究相邻桥跨对系统地震响应的影响,分别选取Taft波和Sanfer波,计算一致激励下有无相邻桥跨的钢轨、桥墩(9号)受力和水平位移,计算结果见图6。
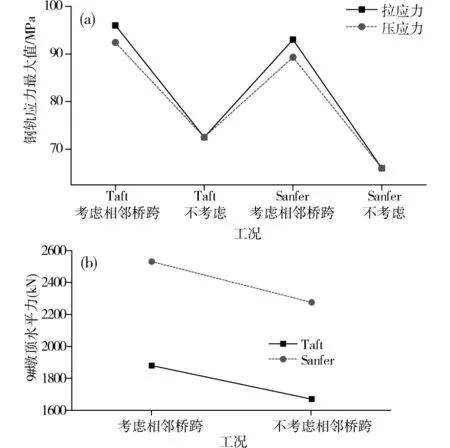
(a)钢轨地震应力最大值;(b)墩顶水平力最大值图6 相邻桥跨对系统地震响应的影响Fig.6 Influence of adjacent bridge span on seismic response of the system
由图6可知,考虑相邻桥跨后,钢轨最大地震应力、墩顶水平力最大值和墩顶水平位移均有所增大。考虑相邻桥跨时,Taft波作用下,钢轨最大地震应力为96.0 MPa(拉),9号墩顶水平力和水平位移最大值分别为1 888.3 kN和76.1 mm。不考虑相邻桥跨时,钢轨最大地震应力为72.5 MPa(拉),9号墩顶水平力和水平位移最大值分别为1 678.6 kN和63.5 mm。
4 设计参数影响分析
为探讨设计参数对系统地震响应的影响,分别对路基段长度、线路纵向阻力和地形这三个参数进行分析,地震波选用Elcentro波,将峰值加速度调整为0.3 g(设计地震)[12],在探讨各参数影响时,其他参数不变。
4.1 路基段长度的影响
为研究路基段长度对系统地震响应的影响,路基段长度分别取0,50,100,150和200 m,选取9号墩顶水平力作为分析对象,计算结果如图7。
由图7可知,随着路基段长度的增大,钢轨地震拉、压应力最大值都在增大,而9号墩底水平力最大值和墩顶最大水平位移在减小,在100 m以后,三者都趋于稳定,此时钢轨地震应力最大为171.0 MPa(拉)和168.0 MPa(压),墩顶水平力为6 697.3 kN,墩顶水平位移为186.3 mm。
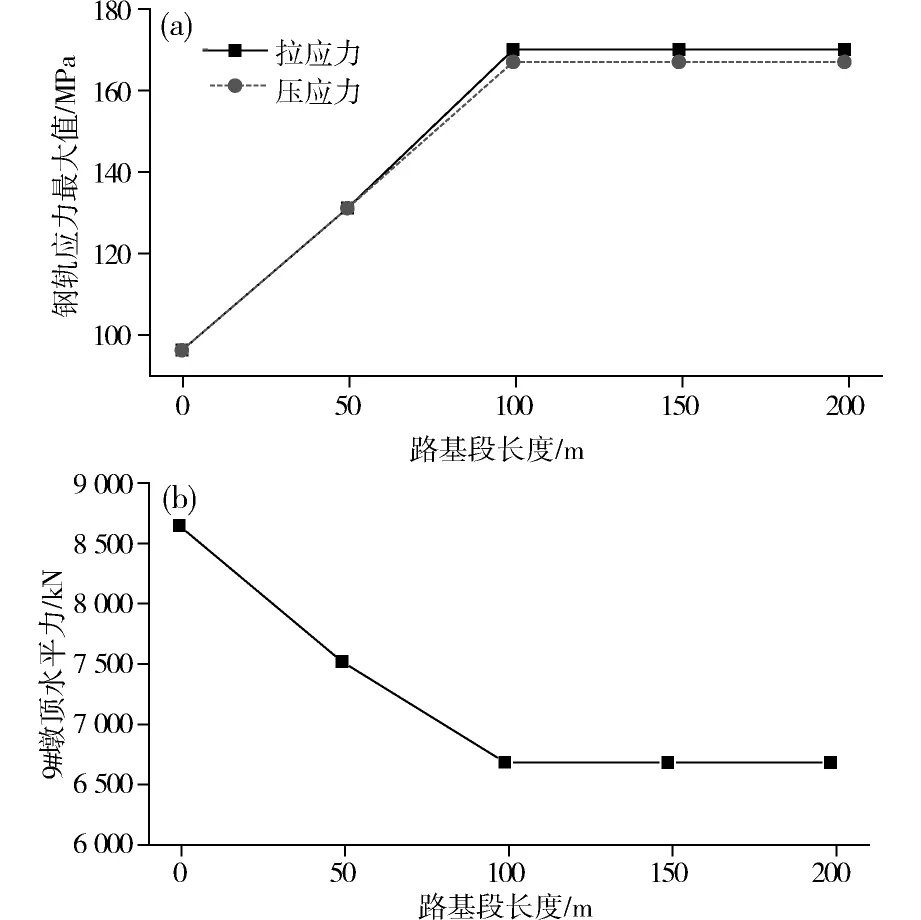
(a)钢轨地震应力最大值;(b)墩顶水平力最大值图7 路基段长度对系统地震响应的影响Fig.7 Influence of the length of the subgrade on seismic response of the system
4.2 线路纵向阻力的影响
为研究线路纵向阻力对系统地震响应的影响,将有砟轨道的线路纵向阻力换成无砟轨道和铺设小阻力扣件时的线路纵向阻力,按式(3)取值,计算结果如图8。
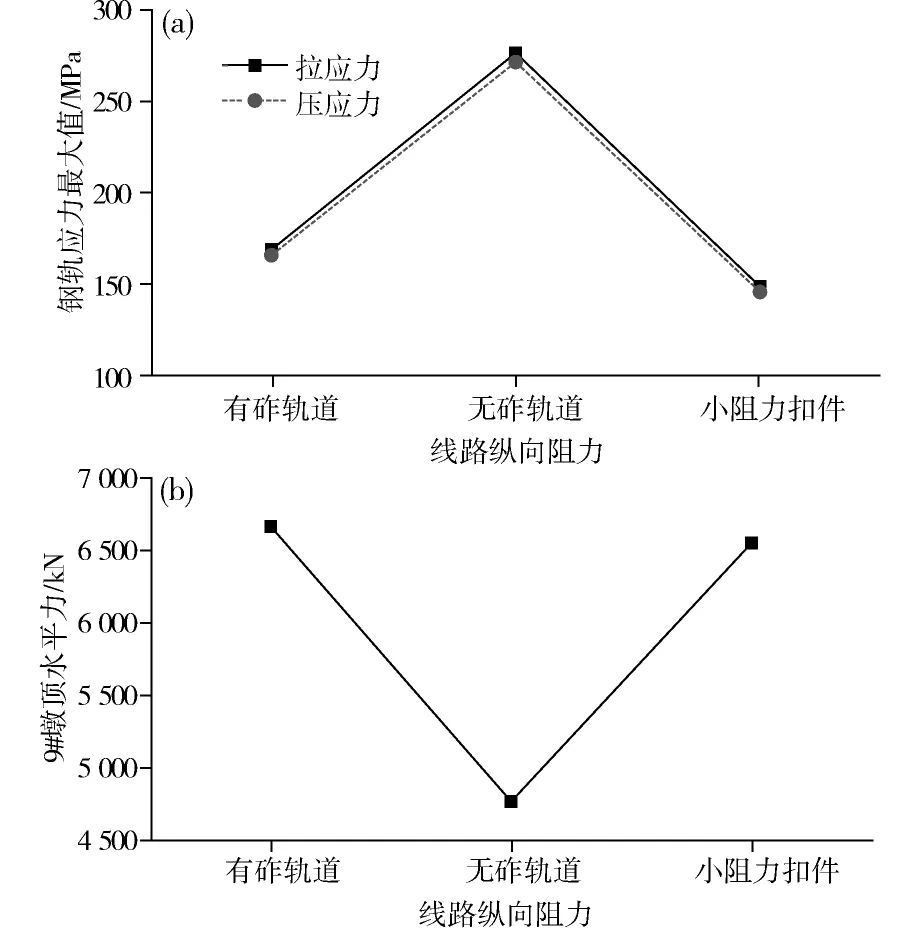
(a)钢轨地震应力最大值;(b)墩顶水平力最大值图8 线路纵向阻力对系统地震响应的影响Fig.8 Influence of the longitudinal resistance of the line on seismic response of the system
(3)
由图8可知,随着线路纵向阻力的增加,梁轨相互作用增强,铺设无砟轨道时,钢轨地震应力为三者最大,对本桥而言,约是有砟轨道的1.6倍,铺设小阻力扣件的钢轨应力最大值较有砟轨道有所减小。
对9号刚构桥制动墩而言,铺设无砟轨道时,墩顶水平力和墩顶水平位移为三者最小,为4 797.5 kN和142.4 mm。铺设小阻力扣件时,墩顶水平力为6 583.2 kN,墩顶水平位移为180.3 mm。
4.3 地形的影响
为研究地形对系统地震响应的影响,仅改变桥墩高度,选择平坦谷地与V型峡谷作比较,地形示意图如图9,计算结果见图10。
由图10可知,桥墩高度对钢轨应力影响不大,随着桥墩高度的增大,墩顶水平力增大。1号-6号和10号-15号桥墩墩顶水平力大幅增大,1号桥墩处增幅最大,从153.1 kN增大到2 978.2 kN。因为7号和16号桥墩处分别是布置了两个活动支座和单独一个活动支座,所以墩顶水平力变化很小。
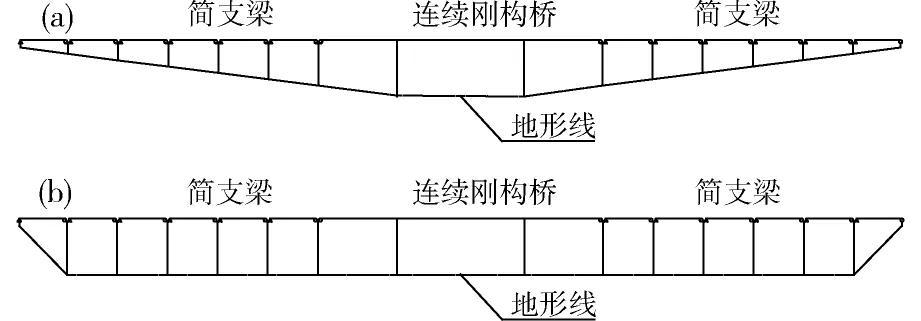
(a)V型峡谷;(b)平坦谷地图9 地形示意简图Fig.9 Topographic sketch map
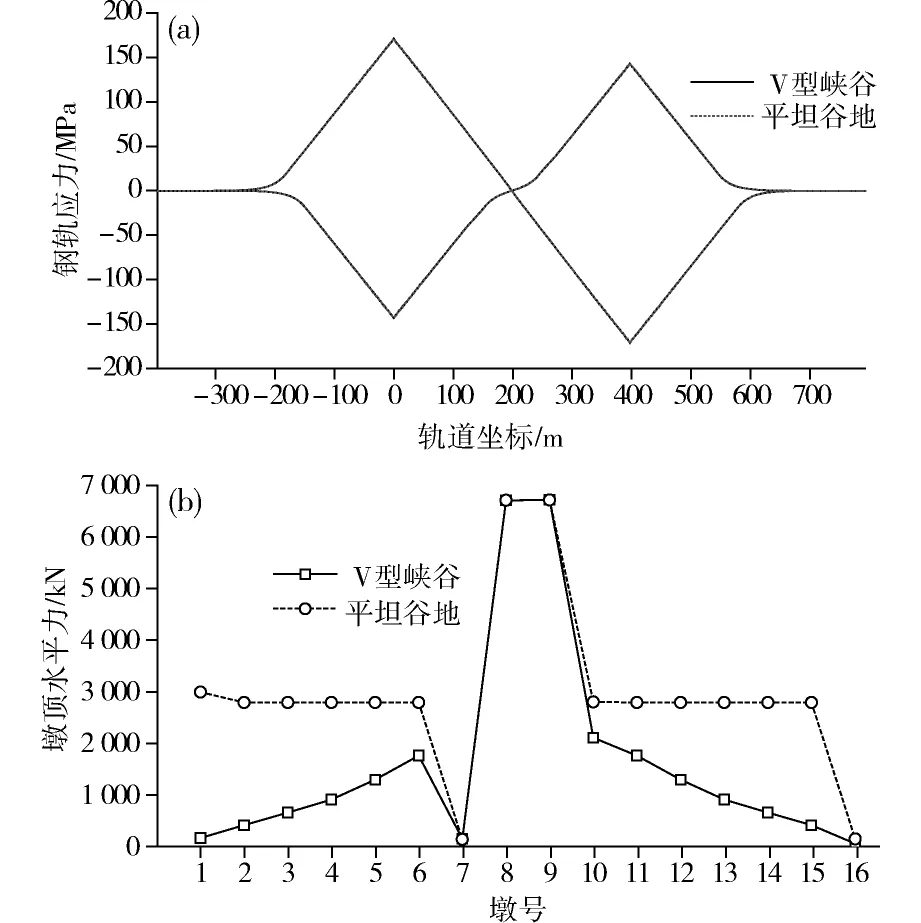
(a)钢轨地震应力包络;(b)墩顶水平力最大值图10 地形对系统地震响应的影响Fig.10 Influence of terrain on seismic response of the system
5 地震与温度荷载耦合作用的探讨
上述地震响应分析时,并没有考虑温度荷载的影响。实际上,地震发生前就可能有温度荷载的作用,需要考虑温度荷载引起的附加力。为探讨地震与温度荷载的耦合作用,分别计算施加地震荷载、施加温度荷载和两者耦合作用下的受力特性,施加温度荷载为梁体升温15 ℃[15],地震波选用Elcentro波,并选取6号-11号桥墩处的钢轨作为研究对象,计算结果见表3和图11。
由表3和图11可知,地震与温度荷载耦合作用下的6号-11号桥墩处的钢轨应力不等于两者单独作用时的钢轨应力之和。因此,简单的将温度荷载作用和地震作用时的钢轨应力线性叠加后的结果认为等于两者耦合作用时的钢轨应力,这是欠考虑的。这是因为桥梁与轨道之间是非线性的相互作用,加载历史是温度荷载先作用在桥梁和轨道系统,然后保留温度荷载及温度变形再进行地震响应,温度荷载是长期缓慢的过程,地震荷载是偶然快速的过程,梁轨之间存在非线性约束,故线性叠加原理不在适用,所以要考虑温度荷载和地震荷载加载历史的影响。
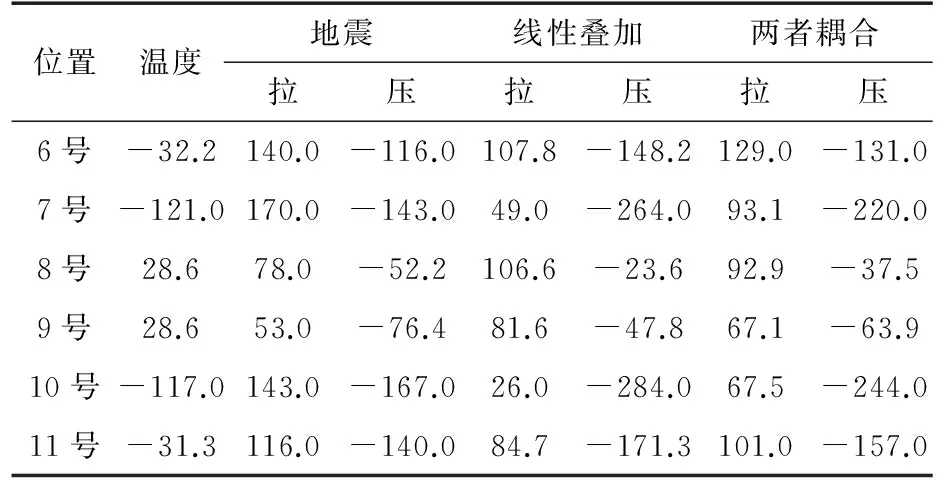
表3 钢轨应力最大值

图11 地震与温度荷载耦合作用Fig.11 Coupling effect of seismic and temperature loads
6 结论
1)桥上轨道的约束作用对系统的低阶自振频率有较大的影响,增幅达47.0%。相邻桥跨也会使系统的自振频率增大,最大增幅达18.0%。因此,在分析系统动力特性时,需要考虑轨道约束和相邻桥跨的影响。
2)地震激励下,系统地震响应与地震频谱特性有关。钢轨地震应力最大值发生在连续刚构桥和简支梁相连处,墩顶水平力最大值和水平位移最大值均是发生在9号刚构桥制动墩处。考虑相邻桥跨后,钢轨最大地震应力、墩顶水平力最大值和墩顶水平位移均有所增大。
3)随着路基段长度的增大,钢轨地震应力最大值增大,墩顶水平力最大值和墩顶水平位移最大值减小,在本文中,路基段长度大于100 m以后,三者都趋于稳定。
4)铺设无砟轨道的时钢轨地震应力最大值大于铺设有砟轨道和小阻力扣件时的钢轨应力,约是有砟轨道的1.6倍,其墩顶水平力最大值和墩顶水平位移最大值是三者中最小的。
5)不同地形(不同桥墩的高度)对钢轨应力影响不大,桥墩高度增大,墩顶水平力增大。
6)桥梁与轨道之间是非线性的相互作用,地震与温度荷载耦合作用时的钢轨应力不等于两者单独作用时结果的线性叠加。
[1] 李宏. 国外重载铁路综述[J]. 铁道工程学报, 2000(4): 32-34. LI Hong. Comprehensive description of heavy haul railways abroad[J]. Journal of Railway Engineering Society, 2000(4): 32-34.
[2] YANG A H. Study on maintenance for heavy haul railway lines[C]// 9th International Heavy Hau l Conference, 2009:308-313.
[3] 戴公连, 朱俊樸, 闫斌. 大跨度重载铁路连续梁桥的小阻力扣件适应性[J].华南理工大学学报(自然科学版),2015,42(4): 48-55. DAI Gonglian, ZHU Junpu, YAN Bin.The adaptability of small resistance fasteners for large span and heavy haul railway continuous girder bridge[J]. Journal of South China University of Technology(Natural Science Edition),2015,42(4): 48-55.
[4] 殷明旻, 易南福, 孟文力, 等. 40t 轴重重载铁路无缝线路纵向附加力研究[J]. 铁道工程学报, 2012, 169(10): 37-42. YIN Mingmin, YI Nanfu, MENG Wenli, et al. Study on additional longitudlmal forces of CWK of heavy haul railway bearing 40 t axle load of vehide[J]. Journal of Railway Engineering Society, 2012, 169(10): 37-42.
[5] 戴公连, 朱俊樸, 闫斌. 30t轴重重载铁路简支梁桥上无缝线路纵向力研究[J]. 土木工程学报, 2015,48(8):59-69. DAI Gonglian, ZHU Junpu, YAN Bin. Study on the longitudinal force of CWR 30t axle load railway bridge[J].China Civil Engineering Journal, 2015,48(8):59-69.
[6] 张永亮, 孙建飞, 徐家林. 高速铁路大跨连续梁桥地震反应分析及抗震校核[J]. 地震工程学报, 2013,35(2):226-231. ZHANG Yongliang, SUN Jianfei, XU Jialin. Analysis of seismic response and seismic checking in a long-span continuous beam bridge on a High-speed Railway[J].China Earthquake Engineering Journal, 2013,35(2):226-231.
[7] 闫斌, 戴公连. 考虑加载历史的高速铁路梁轨相互作用分析 [J]. 铁道学报, 2014,36(6):75-80. YAN Bin, DAI Gonglian. Analysis on the interaction of high speed railway beam and rail considering loading history[J].Journal of the China Railway Society, 2014,36(6):75-80.
[8] 王平, 谢铠泽. 连续刚构桥上无缝线路计算模型及方法的简化[J].中南大学学报,2015,46(7):2735-2744. WANG Ping,XIE Kaize. Calculation model and method of continuous rigid frame bridge with continuous rigid frame bridge[J]. Journal of Central South University, 2015,46(7):2735-2744.
[9] 刘浩, 魏贤奎, 熊震威, 等. 线路纵向阻力形式对桥上无缝线路计算影响[J].铁道标准设计,2013,(10):61-64. LIU Hao,WEI Xiankui, XIONG Zhenwei, et al. Calculation of the effect of line longitudinal drag on the calculation of the bridge[J]. Railway Standard Design, 2013,(10):61-64.
[10] 重载铁路设计规范(征求意见稿)[S]. Code for designing heavy haul railway[S].
[11] Union Interationale Des Chemirs De Fer U. UIC 774-3 Track/bridge interaction. Recanmendations for calcalations[S]. Paris: Ineerational Union of Railways, 2001.
[12] GB50111—2006,铁路工程抗震设计规范[S]. GB50111—2006, Code for seismic design of Railway Engineering[S].
[13] 闫斌, 戴公连, 魏标. 考虑地震行波效应的高铁连续梁桥梁轨互制[J].振动与冲击.2014,33(5):87-90. YAN Bin,DAI Gonglian,WEI Biao. Railway system of high speed railway continuous beam bridge with seismic wave effect[J]. Journal of Vibration and Shock,2014,33(5):87-90.
[14] 黄艳, 阎贵平, 刘林. 轨道约束对铁路桥梁纵向地震反应特性的影响[J].铁道学报.2002,24(5):124-128. HUANG Yan,YAN Guiping,LIU lin.The influence of rail restraint on the longitudinal seismic response of railway bridges[J].Journal of The China Railway Society.2002,24(5):124-128.
[15] TB 10015—2012,铁路无缝线路设计规范[S]. TB10015—2012, Code for design of Railway Continuous Welded Rail[S].
Seismic response of large span continuous rigid frame bridges under heavy haul railway considering track restraint
TU Peng1, ZHOU Wentao1, YAN Bin1,2
(1.School of Civil Engineering,Central South University, Changsha 410075, China;2.National Engineering Laboratory for Construction of High Speed Railway,Changsha 410075, China)
For the study of seismic response law of long span continuous rigid frame bridge and track system in the heavy haul railway, a simulation model for continuous rigid frame bridge and track system considering track restraint under heavy haul railway was established. Taking a 6-32m simply supported beam+(108+180+108) m heavy haul railway continuous rigid-frame bridge +6-32m simply supported beam as an example, the influence of the track constraints and the adjacent bridge span on the self-vibration characteristics was analyzed, and seismic response of the system was studied. The influence of the length of the subgrade, the longitudinal resistance and the topography on the seismic response of the system were also studied. The research shows that track restraint and the adjacent bridge increase the frequency of the system; the seismic response of the system is related to the spectrum characteristics of earthquake; after considering the adjacent bridge, the maximum rail stress, the maximum horizontal force loaded on top and horizontal displacement of pier top increases; with the increase of the length of the subgrade, the maximum value of the stress of the rail increases, and the maximum of the pier horizontal force and horizontal displacement of pier top decreases, and the length of the subgrade should be at least 100m;when the rail laying ballastless track the maximum stress value is greater than the laying of ballasted track and small resistance fastener, the horizontal force of pier top and horizontal displacement of pier top is the minimum of the three cases; with the increase of pier height, the horizontal force of pier top increases; the rail stress of coupling effect of earthquake and temperature loads is not equal to the sum of the two separate effects.
heavy haul railway; track restraint ; adjacent bridge span; continuous rigid-frame bridge; track-bridge interaction; earthquake response
2016-01-03
高速铁路基础研究联合基金资助项目(U13342023);中国博士后科学基金资助项目(2014M552158)
闫斌(1985-),男,河南郑州人,讲师,博士,从事梁轨相互作用方面的研究工作;Email:binyan@csu.edu.cn
U213.912
A
1672-7029(2016)11-2174-07
