列车追踪间隔时间对高速铁路通过能力利用的影响分析

赵欣苗，尹相勇，李茜，高毅，李竹君

(1.北京交通大学 交通运输学院，北京 100044；2.城市交通复杂系统理论与技术教育部重点实验室，北京 100044)



列车追踪间隔时间对高速铁路通过能力利用的影响分析

赵欣苗1,2，尹相勇1，李茜1,2，高毅1,2，李竹君1,2

(1.北京交通大学 交通运输学院，北京 100044；2.城市交通复杂系统理论与技术教育部重点实验室，北京 100044)

列车追踪间隔时间影响高速铁路线路的发车频率，从而影响通过能力。统计分析我国高速铁路和日本东海道新干线的现状运行图中列车追踪间隔时间现状，计算各类列车追踪间隔时间的理论值，并基于现行运行图，制定压缩列车追踪间隔的开行方案。以国内某线路为例，通过仿真法铺画运行图并统计运行指标。研究结果表明：现状运行图的列车追踪间隔时间具有压缩的可能，当现状运行图的到达列车追踪间隔时间压缩到5 min和4 min30 s时，全日区间开行列数从113列分别提高到161列和192列，已超过日本东海道新干线的181列；区间小时开行最大列数从10列分别提高到12列和14列，和日本东海道新干线的14列持平。

高速铁路；通过能力；追踪间隔；开行列数

高速铁路经过多年的运营实践，以其安全、快速、准时和便捷等特点吸引了乘客，目前我国京广、京沪等高速铁路的日行车量已超过110对，列车到达最小追踪间隔达到5 min，然而快速增长的客流量对高铁的运能提出了更高的要求。部分高速铁路区段的上座率已经较高，现场反映开行对数难以增加，出现了能力饱和问题，因此有必要分析我国高速铁路通过能力的利用情况。高速铁路通过能力的定义是：在采取一定数量和类型的动车组和一定的行车组织方法条件下，运营时间内高速铁路区段的各种固定设备在单位时间内(通常1 h或一昼夜)所能通过基准列车的最多列车数或对数[1]。因此本文以列车开行对数来衡量高速铁路的能力水平。

目前国内外学者对线路通过能力的研究较多，国外学者的研究中，Brnnlund[2]研究了不影响通过能力利用的情况下，提高乘客和运营企业的总效益；D’Ariano[3]研究了不影响通过能力利用条件下对列车准时性的提高；Riejos[4]提出了合理的交路设计能够提高通过能力的利用率；由于国外的运输能力超过运输需求，所以研究主要集中在提高乘客的服务质量、减少企业的运营成本等方面，而对高速铁路通过能力利用的研究相对较少；国内学者的研究中，孙焰等[5]研究了列车追踪间隔时间从8 min压缩到7 min时列车开行对数的提高程度，说明压缩列车追踪间隔时间能提高通过能力的利用；张红斌等[6]以京沪线武广段为例，通过加密运行图，提高高速铁路的通过能力，但加密参数中列车追踪间隔按照大于5 min取值；苏顺虎等[7]提出在目前我国高速铁路实际运营条件下，列车追踪间隔时间可以实现3 min，并通过扣除系数法得到线路通过能力为180对以上；Yue等[8]通过优化停站方案和时刻表来提高乘客服务水平和线路通过能力的利用；杨宇正等[9]考虑乘客的弹性需求，计算得到需要开行高速旅客列车191对和中速列车185对；刘敏等[10]对比了仿真法、利用率法和压缩加密法的效果，证明仿真法能更准确地反映车站通过能力的利用情况。

综上所述，线路通过能力通常受到列车追踪间隔时间、停站方案和列车种类等因素的影响，列车追踪间隔时间通常作为约束条件，高速铁路设计规范[11]规定车站间隔时间中，出发和到达间隔时间的最小值是3 min，而我国目前普遍采用5 min计算，可见我国目前应用的列车追踪间隔时间留有比较富裕的安全余量。对列车追踪间隔时间的研究中，田长海等[12]提出了列车追踪间隔时间的计算方法及相关参数取值，说明间隔时间与列车制动和车站咽喉区长度相关，并根据我国高速铁路现场进行了检算；张岳松等[13]综合考虑列车长度、运行速度、常用制动距离、安全防护距离、车站作业时间和闭塞分区长度等影响因素，提出了列车追踪间隔时间的计算方法；上官伟等[14]研究了高速列车不同车型在平直道的常用制动和紧急制动曲线以及对列车追踪间隔的影响；杨欣等[15]提出了满足最高运行速度下制动力与各类列车追踪间隔时间的关系。

本文统计分析了国内外的典型运行图，得到实际运行线路的列车追踪间隔时间现状；借鉴列车追踪间隔时间的研究成果，对列车间隔时间进行理论计算，得到保证安全余量下的理论间隔时间；设计合理的开行方案，并采用仿真方法得到该开行方案开行的列车数量，确定线路通过能力。

1 现状运行图的列车追踪间隔时间分析

列车追踪间隔时间I是指在自动闭塞区段同一方向追踪运行的两列车间的最小间隔时间，包括列车区间追踪间隔时间I追、列车出发追踪间隔时间I发、列车通过追踪间隔时间I通、列车到达追踪间隔时间I到、列车到通追踪间隔时间I到通和列车通发追踪间隔时间I通发等[11]。

分别选取我国高速铁路线路中较为繁忙的线路A和B的某铁路局管段C和D，管段距离分别为626 km和755 km。根据其2014年12月的实际运行图，统计各类列车追踪间隔时间和各区间的分方向列车开行数量等指标，并与日本较为繁忙的东海道新干线(2013年10月)的相关指标进行对比(各线均以下行方向为例)。借助本文编制的运行图仿真与统计分析软件，统计各线路的全部列车追踪间隔时间，按大小分类如表1所示；各线路各区间的全日、分时开行列数如图1所示。

由表1可见，列车追踪间隔时间小于5min的比例中，A线和B线为20%以下，而东海道新干线为46%；且在小于5min的间隔时间中，A线4min以下的比例为39%，B线4min以下的比例仅为20%，而东海道新干线4min以下的比例高达80%。可见，我国高速铁路实际运营中小间隔运用比日本少，实际运营预留了较多安全余量。

表1 列车追踪间隔时间比较

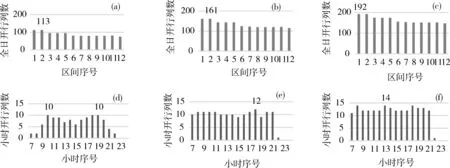
(a) A线C管段全日区间开行列数；(b) B线D管段全日区间开行列数；(c)日本东海道新干线全日区间开行列数(d) A线C管段小时区间最大开行列数；(e) B线D管段小时区间最大开行列数；(f)日本东海道新干线小时区间最大开行列数图1 不同线路各区间开行列数统计Fig.1 Departure frequencies on each sections of different high-speed railways

由图1可见，日本东海道新干线的全日区间最大开行列数达到181列，区间小时最大开行列数达14列；我国高铁A线和B线的全日区间最大开行列数为113和121列，区间小时最大开行列数均为10列。因此，我国高铁的线路通过能力利用与东海道新干线仍有一定差距。

2 理论间隔时间计算方法

根据参考文献[16]计算各类列车追踪间隔时间的理论值，以列车到达追踪间隔时间I到为例说明计算过程，I到是自前行列车到达车站时起，至同方向后行列车到达该站时止的最小间隔时间，包括办理后行列车到达作业的时间和后行列车从监控制动距离运行至站内的时间，如图2所示，计算公式如式(1)所示。

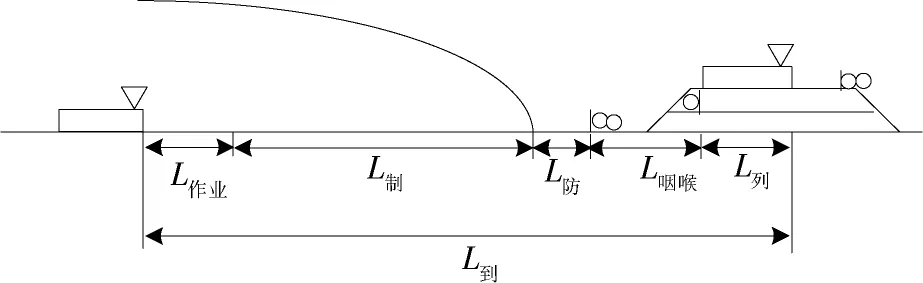
图2 列车到达追踪间隔时间计算条件Fig.2 Calculation condition of train arrival tracking headway

(1)

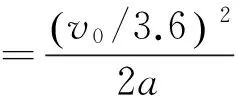
(2)

式中：

I到为列车到达追踪间隔时间，s；

a为列车制动减速度平均值，m/s2；

L制为列控车载设备监控制动距离，即列车从实际最高运行速度v0按a减速制动到0的制动距离，m；

L防为安全防护距离，m；区间取值110 m；车站取值60 m；

L咽喉为车站进站信号机(或出站信号机)至股道反向出站信号机(或反向进站信号机)间的距离，m；

L列为列车长度，m；

v到达为列车到站停车的运行速度，km/h；

t到达为列车到达作业时间，s；CTCS-2级控车取值36 s；CTCS-3级控车取值40 s；

v0为列车实际最高运行速度，即制动初速度，km/h；

分析I到的计算公式及各项参数取值，其中L防、L列和t到达均为定值，L咽喉与车站布置形式有关，L制不固定且取值相对较大。由式(2)可见，在列车最高运行速度v0一定情况下，制动距离L制与列车制动减速度平均值a成反比。分析其他种类列车追踪时间的计算公式，其中：I追、I通和I到通与I到类似，受到L制的影响，且L制与a成反比；I发与I通发与L制无关，不受L制影响。说明制动距离对多种追踪间隔时间具有较大影响，是确定列车追踪间隔时间的一个重要变量。参考文献[16]根据动车组牵引计算软件检算，得到平直道的制动距离为7 509 m，则常用平均制动减速度为0.46 m/s2；因此，本文中制动减速度a采用0.46 m/s2。

3 仿真铺图的算法设计流程

本文编制了运行图仿真与统计软件，在已知列车区间运行时间和列车追踪间隔时间理论值等基础上，以A线C管段下行方向为例，根据提出的开行方案，铺画运行图、调整间隔时间冲突并统计相关指标以检验运行图的铺画效果。

3.1 仿真开行方案内容及设计方法

需要为仿真提供的开行方案内容主要包括：

1)各站各类列车追踪间隔时间的理论计算值。根据参考文献[16]计算列车开行区段不同车站的不同列车追踪间隔时间；

2)各类列车不同状态下的区间运行时间。根据已有实际运行图及调查确定，即按列车等级(G、D等级列车)和列车的区间运行状态(列车在区间前站-后站的状态分别为通过-通过、通过-到达、出发-通过和出发-到达)计算得到8种列车区间运行时间，供计算时选取；

3)列车开行数量(含编组方案)及管内起讫点布局。考虑时空关系与客流的吻合，根据参考文献[1]，起讫点的选择主要根据城市人口规模、社会经济发展程度和区位地理特点等因素，一般选择首都、直辖市、省会城市、连接点以及旅游城市等；并根据现状运行图及客流规律，设定不同类型(直通、管内、高速、动车)列车开行数量及管内起讫点的分布；

4)铺画运行图区段始发站、管内始发站的通过列车及始发列车的通过时刻及始发时刻；

5)列车停站方案。包括经过总站数、停站总站数、停站位置、分时段分区段列车停站比例、最小停站时间以及各次列车在各站的状态(发车、通过、到达或不途经此站)；根据参考文献[1]，停站频率主要根据节点等级划分，重要节点必停，其他节点依据其重要程度交错停站，不同等级列车占总列数的比例根据停站次数要求确定；调整停站车站，应符合分时段分区段列车停站比例；

本论文在开行方案前四项确定的情况下，通过停站方案的停站位置及通过(停车)时刻的不同取值，设计若干方案，其中列车在区段中途站的停站或通过时刻、停站时间以及与前车在车站的间隔类型在仿真软件铺画运行图过程中确定，当仿真方案满足列车开行数量等要求时，能够得出仿真结果；从而可确定此区段不同方案下的某方向开行列车数量，以及该区段某方向的列车通过能力。

3.2 仿真算法流程

本文编制了运行图仿真与统计软件，其中仿真铺画运行图的算法流程如图3所示，某方向运行图铺画仿真的具体步骤为：

step1：输入基础数据，即仿真开行方案，以及各车站某方向的到发线数量；

step2：站序号置1(此方向第一站)，根据开行方案设置区段管内列车始发站或某方向第一站各列车(包括始发、停站和通过列车)的开行时刻；

step3：站序号加1(进入下一站)；

step4：按时间顺序选择经过该站的第1车次号；

step5：根据开行方案判定列车在此站的状态，若为“到达”转到step6，“通过”转到step7，“发车”转到step8；

step6：判断该方向是否有可用到发线，“否”转到step9；“是” 仿真程序记录前一站的状态，并结合后一站的状态，选取列车区间运行时间，得到列车到达本站的时刻，转step10；

step7：仿真程序记录前一站的状态，并结合后一站的状态，选取列车区间运行时间，得到列车通过本站的时刻；转step10；

step8：判断列车与前车在此站形成的间隔时间I发或I通发，是否符合相应种类间隔时间的要求，“否”则延迟发车，并再次判断间隔时间，直到符合要求；“是”转step11；

step9：如果列车需要停在该站，在没有空闲到发线时需在站外等待，直到站内列车发车后有空闲到发线时才能接入列车；如果该列车在上一站的状态是发车而非通过，则在不影响上一站到发的前提下，推迟列车在上一站的出发时间；

step10：如果到达列车或通过列车与前车的间隔时间I到、I通到、I通、或I到通小于对应的理论值，则推迟本次列车到达此站的时刻，即增加站外等待时间以延长区间运行时间；如果列车在上一站的状态是发车，则在不影响上一站到发的前提下，推迟列车在上一站的出发时刻；使列车能够按理论计算间隔值到达或通过该站；

step11：记录到达、通过或发车列车记录；并根据开行方案判断本站车次是否取完：

本站车次取完“是”，则判断是否是终点站，“是”转step12；“否”转step3；

本站车次取完“否”，则按时间顺序取下一车次，车次号+1，转step5；

step 12：记录运行图铺画过程中的仿真指标数据，包括各站实际分类列车追踪间隔时间，列车在站停站时间，列车区段运行时间、列车技术速度、旅行速度和停站比例等，然后仿真结束。

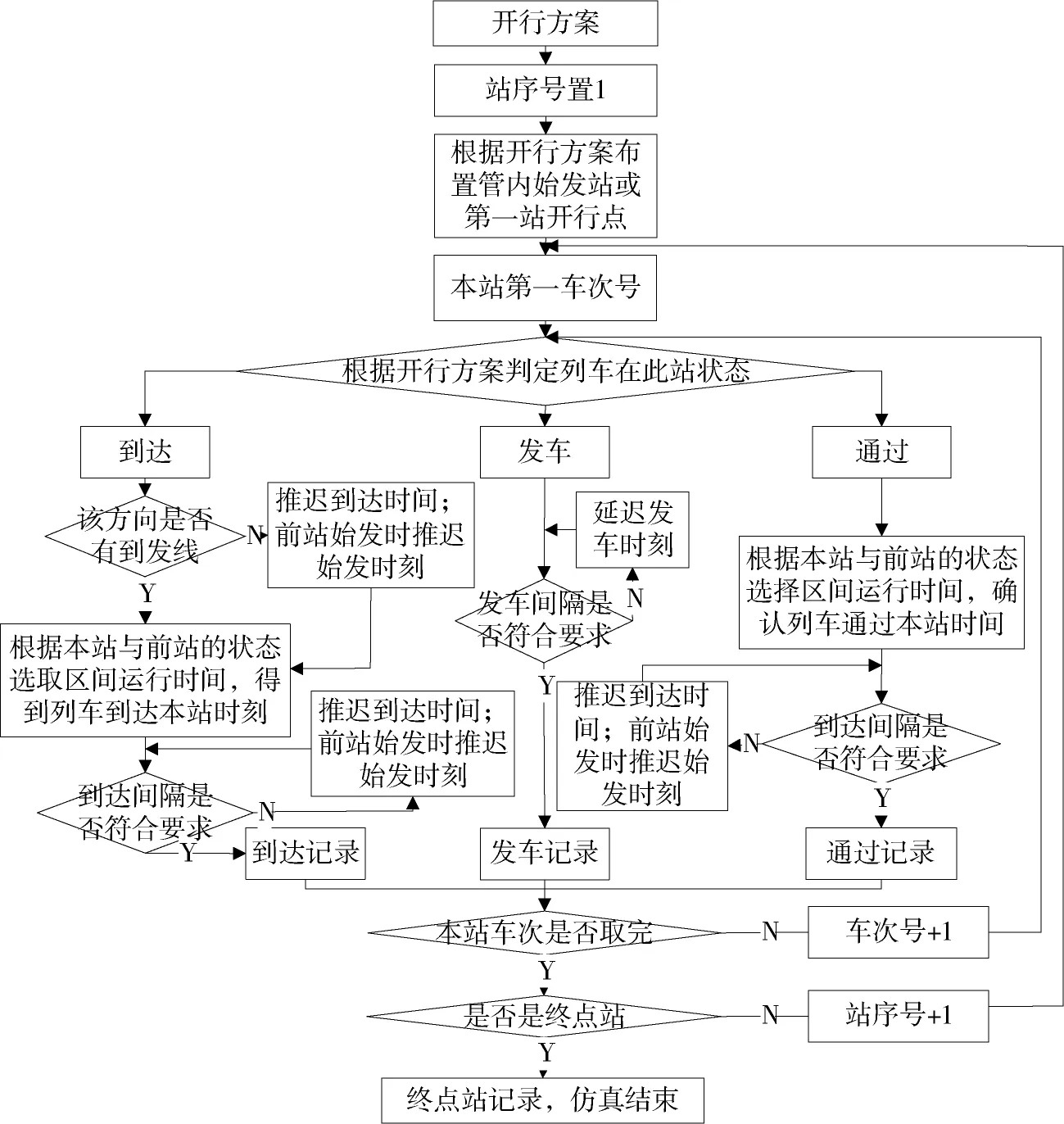
图3 运行图仿真与统计流程图Fig.3 Flowchart of Simulation and statistics on diagrams

4 仿真结果分析

各类列车追踪间隔时间的理论计算公式中，I到、I发和I到通与车站咽喉长度、进站信号机与列车停车标的距离相关，在不同的车站具有不同的理论值，将该理论值作为该类间隔的最小值参照；I通、I通发和I追与车站参数无关，只与闭塞分区长度、列车长度、列车制动距离相关，所以A线C管段各车站选取统一的理论计算值，作为该类间隔的最小值参照。本文中列车制动减速度平均值a取值0.46 m/s2，A线C管段部分车站的各类列车追踪间隔时间如表2所示。

由表2可见，车站咽喉长度不同，同种列车在不同车站的I到、I发、I到通取值不同，但I通、I通发和I追在线路管段取值相同。

以A线C管段为例，以原始运行图(2014年12月)为对照标准，设计在不同间隔时间水平下的新方案。考虑实际运营中，I到取值较大而限制了线路通过能力，所以设计方案1为I到大于5 min的方案，方案2为I到大于4.5 min的方案。运用编制的运行图仿真与统计软件铺画原始运行图和设计方案的运行图，并对列车追踪间隔时间和列车开行对数进行统计，与日本东海道新干线的列车追踪间隔时间统计对比如表3所示。

本文定义的最小间隔数，是指运行图中车站采用的最小列车追踪间隔理论计算值的数量，最小间隔比例是指最小间隔数与运行图中的列车追踪间隔总数的比值。最小间隔比例能够说明运行图铺画的紧密程度，从而反映线路通过能力的利用水平。

表3 A线C管段各方案的间隔时间与日本东海道新干线比较

由表3可见，方案2与原始运行图相比，5 min及以下的间隔比例呈增加趋势，从18%提高到69%；且3 min以下的间隔比例增加，即小间隔的运用比例明显提高；最小间隔比例从18.7%增加到39.8%，反映运行图能力利用水平呈上升趋势。

A线C管段的原始运行图、方案1和方案2与日本东海道新干线的全日开行列数和区间小时最大开行列数如表4和图4所示。

表4 A线各方案的开行列数与日本东海道新干线比较

(a)原始运行图全日区间开行列数；(b)方案1全日区间开行列数；(c)方案2全日区间开行列数(d)原始运行图小时区间开行列数；(e)方案1小时区间开行列数；(f)方案2小时区间开行列数图4 不同方案仿真运行图的区间开行列数Fig.4 Departure frequencies on each sections of different solutions

由表4和图4可见，当原始运行图的列车到达追踪间隔时间最小取值为5 min和4.5 min时，全日区间发车列数从113列提高到161列和192列，与文献[7]中通过扣除系数法，在追踪间隔为3 min时，通过能力基本在180对以上相符。最大区间的最大小时发车列数从10列提高到12列和14列，说明提高了线路通过能力。东海道新干线的统计时段是6:01-23:33，A线C管段的统计时段是7:10-23:53，在统计时段基本相同的情况下，方案2的区间最大列数已超过东海道新干线运行图列数水平，区间小时最大发车列数与东海道新干线持平，部分区间仍有增加列数的可能。各方案全程运行列车比例在50%以上，新方案中长短线列车均衡增加，符合前文对开行方案的设计原则，使新开行方案下的运行图具有较好的时空关系。

5 结论

1)日本东海道新干线对较小列车追踪间隔时间的应用比我国高铁线路更为普遍；与理论计算值相比较，实际运营应用的列车追踪间隔时间仍有压缩空间；

2) 列车到达追踪间隔时间从原始运行图压缩到5 min和4.5 min时，较小列车追踪间隔时间的比例有所提高，全日区间开行列数从113列提高到161列和192列，在统计时段基本接近的情况下，已超过日本东海道新干线的181列；区间小时最大开行列数从10列提高到12列和14列，和日本东海道新干线的14列持平；说明压缩列车追踪间隔时间指标，能够较为明显地提高高速铁路通过能力。

[1] 彭其渊, 文超. 高速铁路运输组织基础[M]. 成都: 西南交通大学出版社, 2014. PENG Qiyuan, WEN Chao. Transportation organization of high speed railway[M], Chengdu: Southwest Jiaotong University Press, 2014.

[2] Brännlund U, Lindberg P O, NU A, et al. Railway timetabling using lagrangian relaxation[J]. Transportation Science, 1998, 32(4):358-369.

[3] Ariano D A, Pacciarelli D, Pranzo M. Assessment of flexible timetables in real-time traffic management of a railway bottleneck[J]. Transportation Research Part C, 2008, 16(2):232-245.

[4] Riejos F A O, Barrena E, Ortiz J D C, et al. Analyzing the theoretical capacity of railway networks with a radial-backbone topology[J]. Transportation Research Part A, 2015, 84:83-92.

[5] 孙焰, 董志国, 季令,等. 沪宁线追踪间隔“8改7”对通过能力的影响[J]. 同济大学学报(自然科学版),2001, 29(4):453-457. SUN Yan, DONG Zhiguo, JI Ling, et al. Analysis of the dffect on the carrying capacity when train trace headway shortened from 8 to 7 on Line Hu Ning[J]. Journal of Tongji University (Natural Science), 2001, 29(4):453-457.

[6] 张红斌, 董宝田. 基于能力计算的运行图加密问题研究[J]. 交通运输系统工程与信息, 2011, 11(4):129-134. ZHANG Hongbin，DONG Baotian. Railway timetable saturation based or capacity calculation[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(4):129-134.

[7] 苏顺虎, 田长海, 陈治亚. 客运专线通过能力的分析计算[J]. 中国铁道科学, 2008, 29(5):119-124. SU Shunhu, TIAN Changhai, CHEN Zhiya. Analysis and calculation of the carrying capacity on Passenger Dedicated Lines[J]. China Railway Science, 2008, 29(5):119-124.

[8] Yue Y X. Optimizing train stopping patterns and schedules for high-speed passenger rail corridors[J]. Transportation Research Part C, 2016, 63(2):126-146.

[9] 杨宇正, 周文梁. 基于弹性需求的高速铁路列车开行方案优化[J]. 铁道科学与工程学报, 2012,9(3):34-38. YANG Yuzheng, ZHOU Wenliang. Optimization of train plan on high-speed railway based on elastic demand[J]. Journal of Railway Science and Engineering, 2012，9(3):34-38.

[10] 刘敏, 韩宝明, 李得伟. 高速铁路车站通过能力计算和评估[J]. 铁道学报, 2012, 34(4):9-15. LIU Min，HAN Baoming，LI Dewei. Calculation and evaluation of carrying capacities at high-speed railway stations[J]. Journal of China Railway Science, 2012, 34(4):9-15.

[11] TB 10621-2014，高速铁路设计规范条文说明[S]. TB 10621-2014， Code fordeisign of high-speed railway[S].

[12] 田长海, 张守帅, 张岳松, 等. 高速铁路列车追踪间隔时间研究[J]. 铁道学报, 2015, 37(10): 1-6. TIAN Changhai, ZHANG Shoushuai, ZHANG Yuesong, et al. Study on the train headway on automatic block sections of high-speed railway[J]. Journal of China Railway Science, 2015, 37(10): 1-6.

[13] 张岳松，田长海，姜昕良，等. 高速铁路列车间隔时间的计算方法[J]. 中国铁道科学, 2013, 34(5):120-125. ZHANG Yuesong，TIAN Changhai，JIANG Xinlian, et al. Calculation method for train headway of high speed railway[J]. China Railway Science, 2013, 34(5):120-125.

[14] 上官伟, 蔡伯根, 王晶晶, 等. 时速 250km 以上高速列车制动模式曲线算法[J]. 交通运输工程学报,2011, 11(3): 41-46. SHANGGUAN Wei, CAI Baigen, WANG Jingjing, et al. Braking mode curve arithmetic of high-speed train above 250 km/h[J]. Journal of Traffic and Transportation Engineering, 2011, 11(3): 41-46.

[15] 杨欣, 邵林, 邵军, 等.基于列车追踪间隔时间的高速动车组制动能力计算方法[J]. 中国铁道科学, 2013, 34(06): 99-104. YANG Xin, SHAO Lin, SHAO Jun, et al. Calculation method for braking capacity of high-speed EMU based on train tracking headway time[J]. China Railway Science, 2013, 34(06): 99-104.

[16] Q/CR 471-2015，高速铁路列车间隔时间查定办法[S]. Q/CR 471-2015, Determination method for the train headway on high-speed railway[S].

Influence of train tracking headways on carrying capacity utilization of high-speed railway

ZHAO Xinmiao1,2，YIN Xiangyong1，LI Xi1,2, GAO Yi1,2, LI Zhujun1,2

(1. Department of Traffic and Transportation; Beijing Jiaotong University, Beijing 100084, China;2. MOE Key Laboratory for Urban Transportation Complex Systems Theory and Technology, Beijing Jiaotong University, Beijing 100044, China)

Train tracking interval times affect departure frequencies and carrying capacity utilization of high-speed railway lines. This paper analyzed current train interval times of high-speed railways in China and Japan by statistical method, and new train planning was designed by compressing train tracking intervals based on current diagrams. A real line in China was taken as an example to study the diagrams of new train planning by simulation. The analysis on train tracking interval times and departure frequencies shows that there's still space for compressing train tracking intervals. When they're compressed to 5min and 4min30s, the departure frequencies of full-day increase from 113 to 161 and 192 respectively, in which the latter one has surpassed Japan Tokaido Shinkansen(181); and the maximum hourly departure frequencies increase from 10 to 12 and 14 respectively, in which the latter one has cought up with Japan Tokaido Shinkansen(14).

high-speed railway;carrying capacity; headway; departure frequency

2016-02-22

国家重点基础研究发展计划(973)计划资助项目(2012CB725406)；国家自然科学基金重大资助项目(71390332，71571016)

尹相勇(1957-)，男，北京人，教授，博士，从事交通运输规划与管理研究；E-mail: xyyin@bjtu.edu.cn

U291

A

1672-7029(2016)11-2099-08