车载下大跨度桥梁动力可靠度评估

鲁乃唯, 罗 媛, 汪勤用, Noori Mohammad

(1. 东南大学 土木工程学院,江苏 南京 210096; 2. 长沙理工大学 土木与建筑学院, 湖南 长沙 410114)



车载下大跨度桥梁动力可靠度评估

鲁乃唯1, 罗 媛2, 汪勤用2, Noori Mohammad1

(1. 东南大学 土木工程学院,江苏 南京 210096; 2. 长沙理工大学 土木与建筑学院, 湖南 长沙 410114)

为了评估大跨度桥梁在车流荷载作用下的适用性,基于某高速公路车流监测数据建立随机车流模型,分析在3种随机车流作用下悬索桥位移的动力可靠度.采用车-桥耦合振动分析方法求解桥梁动力响应,以位移首次超越准则估算失效概率,并分析密集车流占有率对桥梁可靠度的影响规律.结果表明：在随机车流作用下,悬索桥主梁动力响应均值的最大值位于跨中位置,响应均方根最大值位于1/4跨径位置；大跨度桥梁运营期位移超限的适用性可靠度与密集车流的占有率相关；随机车流荷载模型包含车流的概率特征,可用于大跨度桥梁动力响应的概率建模,且在桥梁动力可靠度评估中有一定的适用性.

动力可靠度；随机车流；悬索桥；动态称重；首次超越；均方根；车-桥耦合振动

近年来,随着交通运输行业的不断发展,车辆数量与载重量日益增长,直接影响到既有桥梁的运营安全水平.美国的I-35桥和我国哈尔滨阳明滩匝道桥在重载车流作用下的倒塌事故引起了国内外学者的高度重视[1].我国设计规范中的车辆荷载标准是根据九十年代的车辆统计数据制定,其有效性有待于与现有车辆的统计数据校准，因此,亟需评估现有重载交通荷载作用下既有桥梁的安全性与适用性.

大跨度桥梁的车辆荷载效应与中小跨度桥梁有着显著的区别,主要表现如下：大跨度桥梁主梁刚度低,在荷载作用下主梁变形较大；大跨度桥梁位于交通咽喉位置,车流量较大；大跨度桥梁受车辆密集程度影响较大.大量车流作用致使桥梁构件剧烈振动,该动力效应首次超过某个界限值时就形成首次超越失效[2].基于动力可靠度理论的首次超越准则用于评估车流作用下桥梁的安全性具有较好的适用性.然而,现有随机车流作用下桥梁的动力响应分析侧重于桥梁动力行为[3]、冲击系数[4]和行车舒适性[5]研究,鲜有应用随机车流模型至桥梁动力响应概率分析与结构安全评估.Xiang等[6]采用静力可靠度的方法评估了单个车辆-桥梁耦合振动系统的可靠度,但忽略了随机振动与车流效应对桥梁动力响应的影响.Ettefagh等[7]研究了车辆参数的不确定性对桥梁动力响应统计参数的影响规律,认为重载车辆对桥梁动力响应特征值有更大的影响.孟阳君等[8]基于成桥荷载试验分析了标准车辆作用下连续刚构桥的首超可靠度,但缺少考虑随机车流作用.在桥梁工程领域,首超可靠度理论主要用于研究地震荷载作用下桥梁的动力可靠度[9].事实上,首超准则同样可应用于随机车流作用下大跨度桥梁动力可靠度评估.由上述研究现状可知,随机车流-桥梁耦合振动和桥梁动力可靠度等领域均取得了丰硕的研究成果,尚缺少随机车流作用下大跨度桥梁的首超动力可靠度研究.

为了基于实测车流数据评估大跨度桥梁的适用性,提出随机车流作用下的适用可靠度分析方法.基于某高速公路实测车流数据建立随机车流模型,并用于分析桥梁动力响应的概率特征.以位移首次超越为失效准则,评估某悬索桥在3种模拟车流作用下的可靠度.分析密集车流占有率对桥梁位移首次超越失效概率的影响规律.

1 基于WIM与CA的随机车流模拟

随机车流是一种将车辆参数(如：车型、车重、车距和车速等)取为随机变量,采用一定的抽样方法在时域内生成随机车辆,用以模拟实际交通状况的模型.模拟方法主要是Monte-Carlo抽样和随机过程方法[10].为了更加真实地模拟车流变化特征,本文采用桥梁动态称重(weigh-in-motion, WIM)数据与元胞自动机(cellular automation, CA)技术模拟高速公路桥梁的随机车流.

1.1 基于动态称重的车辆概率模型

WIM系统是安装在路面面层以下的一套传感器系统,用以获取通过车辆的轴重、车速和车型等参数.随着传感器技术的迅速发展,目前的WIM系统具有较高的控制精度,通过WIM系统的大量统计数据可建立车辆的概率模型.

宜泸高速公路南溪长江大桥WIM系统在2013年3月1日至同年7月31日(共计153 d)监测到约107万辆车.根据车辆的轮轴配置,将所有车辆划分为V1～V6六种类型[11],并统计每种车型的参数概率特征.V1车型表示小型客车,V2～V6车型表示2轴～6轴货车.统计结果表明：车型服从均匀分布,车速服从正态分布,车重概率密度函数具有多峰特征,车距具有显著的随时变性.根据统计数据,采用高斯混合模型(Gaussian mixture model, GMM)拟合每种车型的每个轴重.以6轴车型的第2个轴重(W62)为例,其概率密度函数如图1所示.图中,PDF表示概率密度.

图1 6轴车型第2个轴重概率密度分布Fig.1 Probability density distribution of axle weight of 2nd axel of 6-axle trucks

车距的概率分布随着时间变化较大,且车距与车辆的密度相关,直接影响到桥梁的动力响应.根据车距概率统计特征将车辆运行状态划分为3种：稀疏状态、一般状态和密集状态.目前针对这3种状态并无明确的界限划分标准，如宗周红等[12]建议以2 s的时距划分车辆的密集与稀疏状态.本文采用以下划分准则：稀疏状态的车距，>500 m；一般状态的车距，100～500 m；密集状态的车距，<100 m.密集状态车辆车距的概率密度函数可采用Gamma函数进行拟合,如图2所示.其中,Gamma函数的k与θ值分别为6.43与9.15,D表示同一车道内前、后两辆车的间距.

车速的概率特征与车型以及车辆的密集状态有关.统计数据表明：在稀疏运行状态下,V1车型车速服从均值为87 km/h器、标准差为13 km/h器的正态分布；V6车型车速服从均值为66 km/h器、标准差为8.3 km/h器的正态分布；在密集运行状态下,每种车型的车速均服从均值为52 km/h器、标准差为4.3 km/h器的正态分布.由于车速具有时变性,该概率模型仅用于生成车辆的初始车速.

图2 密集运行状态下车距概率分布Fig.2 Probabilistic distribution of vehicle gaps under busy traffic flow

1.2 基于元胞自动机的随机车流模拟方法

图3 基于元胞自动机(CA)的随车流示意图 (vi=2 cell/s)Fig.3 Sketch of random traffic flow based on cellular automation (CA) model (vi=2 cell/s)

在建立概率密度函数之后,采用合适的抽样方法可生成随机车流模型.由于Monte-Carlo抽样方法是根据概率密度函数进行随机抽样,车辆样本的参数不随时间变化.然而,实际车辆在行驶过程中会有加速、减速、更换车道等行为,Monte-Carlo方法无法模拟这些行为.CA方法在此具有较好的适用性,基于CA方法的随机车流模拟原理[13]如图3所示.图中,桥梁的车道被划分为多个大小相等的元胞,每个元胞在t时刻仅容纳一辆车,车速可通过每个时间间隔行驶过的元胞表示.3号车辆在单位时间内通过了2个元胞,表示以正常速度行驶；1号车辆在单位时间内通过了3个元胞,表示加速行驶;2号车辆在单位时间内通过1个元胞,表示减速行驶.

根据某高速公路桥梁WIM的车辆统计数据与CA模型建立密集运行状态下的随机车流模型，如图4所示.图中,每个点表示一辆车,T为每辆车的相对行驶时间,D为车辆在桥梁上的相对距离.CA模型的相关参数如下：元胞长度为5 m,时间步长为1 s,元胞数量为200个,车辆密度为2.7%,变更车道的概率为10 %.基于CA的密集车流模型更加真实地描述出了车辆在桥梁的运行状态,如：加速、减速和变更车道等,也包含了车辆的密度信息,更加真实地反应了交通特征.CA交通模型模拟的交通流荷载作用以及桥梁动力响应特征可参考文献[14].

图4 基于CA模拟的密集车流样本Fig.4 Busy traffic flow sample simulated based on CA model

2 随机车载下大跨度桥梁首超可靠度分析方法

在大跨度桥梁的首超可靠度评估领域,主要的研究方法是基于频域的响应谱和虚拟激励方法.然而,由于车-桥系统振动响应需要在时域内求解,车载下桥梁的首超动力可靠度分析无法沿用抗震首超可靠度方法.

本文提出一种随机车载下大跨度桥梁首超可靠度分析方法,主要包括3个关键步骤：基于有限元的车流-桥梁动力响应分析、动力响应的概率统计分析、首超可靠度分析.该方法的分析框架如图5所示.

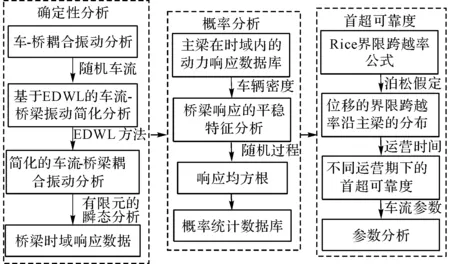
图5 随机车流下大跨桥梁的首超可靠度评估框架Fig.5 Framework for first-passage reliability assessment of long-span bridges under stochastic traffic flow

2.1 确定性动力响应分析

目前,车-桥耦合振动的分析模型较为成熟.根据车辆与桥梁的位移与作用力的耦合关系可得到两者的耦合运动方程[15]：

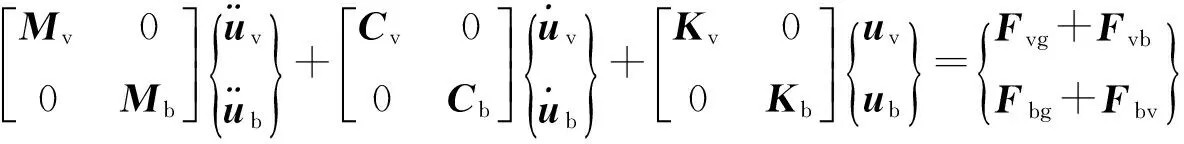
(1)

与中小跨径桥梁相比,大跨度桥梁刚度较低,车-桥耦合振动效应不明显,但应考虑多个车辆对桥梁产生的影响.Chen等[16]的研究结果表明,当车流通过桥梁时,车辆与桥梁之间的互相作用力受前后车辆的影响较小,因此可单独提取每个车辆与桥梁的相互作用力的时变力.Chen等[16]据此提出了等效动态轴重荷载(equivalent dynamic wheel load, EDWL)方法,表达式为

(2)

(3)

式中：Rj和Gj分别表示第j辆车的动态轴重比和自重,xj和dj分别表示第j辆车在桥梁上的纵向位置和横向位置.

采用上述EDWL方法可将车辆的每个轴重转换为等效的时变集中力,为基于有限元的桥梁动力响应瞬态分析提供了有利条件.

2.2 动力响应的概率统计分析

随机车流模型中包含着车辆的概率统计特征,经过车-桥耦合振动分析得到的桥梁动力响应也应具有一定的概率特征.此外,动力响应的均方根值也是Rice界限跨越率计算的一项重要内容.

根据对密集车流、一般车流和稀疏车流的划分,对每种车流进行统计分析.在每个时间段内,采用不同的随机车流类型,例如：在上、下班时间段采用密集车流模型、凌晨时间段采用稀疏车流模型、其余时间段采用一般流模型.虽然车辆在每天的不同时间段内是不平稳的,但在某个区间段内具有平稳特征,通过随机车流区间的划分就解决了车辆的不平稳随机过程特征.

假定某种随机车流作用下桥梁的动力响应采用随机过程表示为X1,将其划分为n个区间段X1=(x1,x2,…,xn).每个区间段的均值Exi及均方根(root-mean-square, RMS)σxi可表示为

(4)

式中：Ts表示该时间段内的时间大小,在Ts足够大时,可采用动力响应的均值表示桥梁动力响应的随机过程期望值.

2.3 首超可靠度

在获取桥梁动力响应概率统计特征值之后,即可进行首超可靠度分析.首超可靠度表示为随机过程X(t)在某个时间段t内超越某个界限a的概率,表达式为

(5)

式(5)的精确求解极为困难,目前主要采用Rice基于Poisson假定提出的跨越率公式[17]：

(6)

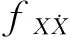
(7)

随机车流作用下某时间段内桥梁动力响应为非零均值的平稳随机过程,且动力响应值远小于界限a,因此,式(7)中A=1,再引入桥梁动力响应均值Ex,则可得到界限跨越率：

(8)

结合式(5)～(8)可得到多种随机车流作用下桥梁首超可靠度的数学表达式：

(9)

式中：根据不同的随机车流特征将时间T划分为n段,每段由ti表示,vi和ρi分别表示第i种随机车流作用下桥梁的界限跨越率与密度.

3 工程实例

以主跨为820 m的南溪长江大桥为工程背景,阐述本文提出的随机车流作用下大跨度桥梁首超可靠度分析方法.

3.1 工程背景

南溪长江大桥是位于四川省宜泸高速公路的一座双塔单跨钢箱梁悬索桥,于2012年建成通车,并安装有健康监测系统与车辆动态称重系统,桥型布置如图6所示.

桥梁设计荷载等级为公路-I级,主缆成桥后的垂跨比为1∶10,桥面宽度为29.78 m,主缆采用预制平行钢丝索股级成,通长索共87股,每股由直径为5.1 mm的高强镀锌钢丝组成.主梁为钢箱加劲梁结构,共65个梁段.索塔为门式框架结构.采用ANSYS软件建立的有限元模型如图7所示,其中,主梁与索塔为Beam44单元,主缆与吊杆为Link10单元,二期恒载为Mass21单元.路面平等级取为“好”,相应的系数取为20×10-6m3/cycle,采用三角级数法[18]得到的路面平整度Rrou如图8所示.

图6 南溪长江大桥桥型布置图Fig.6 Layout of configuration of Yangtze River Bridge in Nanxi

图7 南溪长江大桥有限元模型Fig.7 Finite element model of Yangzi River Bridge in Nanxi

图8 路面平整度的模拟样本Fig.8 Sample of simulated road surface roughness

通过调整桥面二期恒载与主缆初张力,使得该模型的竖向自振频率与实测频率误差小于5%.其中,1～5阶竖向自振频率分别为0.187、0.244、0.320、0.408和0.482.

3.2 桥梁动力响应概率分析

在采用有限元进行瞬态分析之前,需要采用EDWL方法计算车辆的动态轴重系数,并将该动态系数结合车重以时变节点力的形式输入有限元模型.取悬索桥主梁L/4和L/2节点为例,在10 min内3种随机车流模型分别作用下悬索桥主梁位移响应时程曲线如图9所示.由图9可知,随机车流作用下悬索桥加劲梁L/4位移响应数值明显大于L/2位置,密集车流作用下加劲梁的位移响应值大于稀疏车流与一般车流.为了获取稳定的统计结果,采用3种随机车流各1 h的时程分析数据.其中,密集车流、一般车流、稀疏车流的样本容量分别为480、264及117辆.

由式(4)计算如图9所示位移时程的概率统计特征值,均值μy与均方根σy沿主梁的分布如图10所示.由图10可知,密集车流下主梁的均值与均方根值明显大于一般车流与稀疏车流,主梁L/2处的位移均值最大,而主梁L/4处的RMS值最大.主梁的RMS值呈“M”形分布,其主要原因为悬索桥主梁的一阶竖向振形是反对称形状,主梁L/4与3L/4的模态值最大.

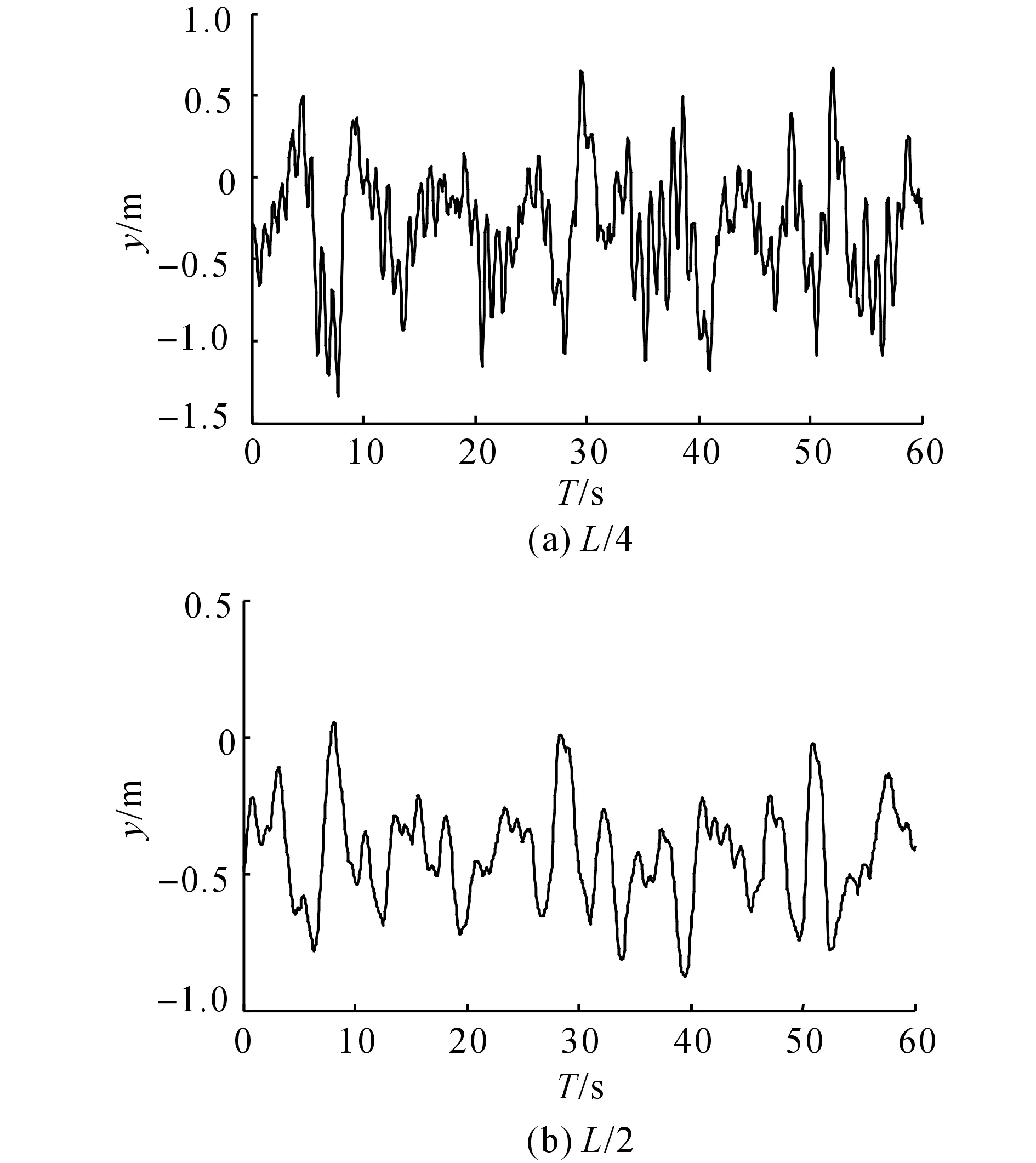
图9 随机车流作用下悬索桥主梁位移时程Figs.9 Displacement time history of the suspension bridge under stochastic traffic flow

图10 主梁位移统计参数Figs.10 Statistic parameters of girder displacements

3.3 首超可靠度分析

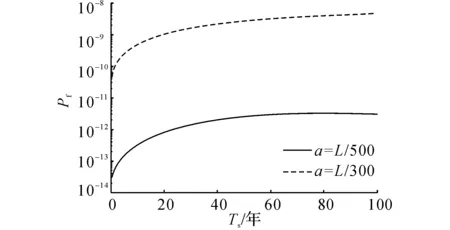
图11 主梁位移首次超越失效概率Fig.11 First-passage failure probabilities of girderdisplacements

获得主梁的动力响应概率统计特征后,由式(9)可计算界限跨越率与不同运营期内的失效概率以及可靠指标.针对位移界限值a的选取,朱劲松等[19]针对大跨度斜拉桥的可靠度计算采用了L/500,我国最新的悬索桥设计规范[20]规定位移界限值为L/300～L/250.本文分析取车辆荷载作用下桥梁位移上限值a分别为L/500和L/300,则由7%占有率(由WIM数据统计得出)的密集车流作用下悬索桥的位移首超失效概率如图11所示.由图11可知,随着桥梁服役时间的增长,桥梁的首超失效概率逐步增长,但是增长率逐步趋于平缓.针对第100年的失效概率,当a=L/500时,Pf=4.9×10-9；当a=L/300时,Pf=2.9×10-12.由此可知,位移界限值的选取对失效概率的计算结果具有较大的影响.下文将选取a=L/300进一步研究密集车流参数对首超可靠度的影响规律.

上述研究未考虑密集车流占有率随运营时间的变化.事实上,随着社会经济发展,密集运行车辆占有率会逐步增加.考虑到密集车辆占有率在运营期内的增长规律,分别取密车流占有率为7%、14%和21%,由此得到主梁位移首超可靠指标变化规律如图12所示.图中,β为可靠指标，当密集车辆占有率为7%、14%、21%时,主梁第100年的首超可靠指标分别为7.25、7.13、7.06.随着密集车辆占有率的增长,主梁位移首超可靠指标迅速下降,但随着密集车辆占有率的持续增长,该下降趋势有所减缓.

图12 密集车流占有率对首超可靠指标的影响Fig.12 Influence of occupancy of busy traffic flow on first-passage reliability index

4 结 论

(1) 基于实测交通数据的随机车流为大跨度桥梁交通荷载模拟提供了有效概率模型,结合确定性的车桥耦合振动分析与首次超载概率模型可用于评估大跨度桥梁适用可靠度.

(2) 车流荷载作用下悬索桥的位移均值的最大值位于跨中,而响应均方根最大值位于1/4跨,位移首次超越失效事件关键位置位于1/4跨.

(3) 密集车流占有率是影响大跨度桥梁适用可靠度的重要因素,其可靠指标随密集车流占有率的增长而降低.

由于首次超越模型采用了较为经典的Possion假定,该模型的精确性有待进一步考查.此外,本研究未考虑桥梁运营期内的车辆增长模型,有待基于长期车辆监测数据建立车辆荷载与交通量的增长模型.

[1] DENG L, WANG W, YU Y. State-of-the-art review on the causes and mechanisms of bridge collapse [J]. Journal of Performance of Constructed Facilities,2016, 30(2):04015005．

[2] BU J, LAW S, ZHU X. Innovative bridge condition assessment from dynamic response of a passing vehicle [J]. Journal of Engineering Mechanics, 2006, 132(12): 1372-1379．

[3] CHEN S, WU J. Dynamic performance simulation of long-span bridge under combined loads of stochastic traffic and wind [J]. Journal of Bridge Engineering, 2009, 15(3): 219-230．

[4] 韩万水,闫君媛,武隽,等.基于长期监测的特重车交通荷载特性及动态过桥分析[J].中国公路学报,2014,27(2): 54-61． HAN Wan-shui, YAN Jun-yuan, WU Jun, et al. Extra-heavy truck load features and bridge dynamic response based on long-term traffic monitoring record [J]. China Journal of Highway and Transport, 2014, 27(2): 54-61．

[5] CAMARA A, NGUYEN K, RUIZ-TERAN A, et al. Serviceability limit state of vibrations in under-deck cable-stayed bridges accounting for vehicle-structure interaction [J]. Engineering Structures, 2014, 61: 61-72．

[6] XIANG T, ZHAO R, XU T. Reliability evaluation of vehicle-bridge dynamic interaction [J]. Journal of Structural Engineering, 2007, 133(8): 1092-1099．

[7] ETTEFAGH M, BEHKAMKIA D, PEDRAMMEHR S, et al. Reliability analysis of the bridge dynamicresponse in a stochastic vehicle-bridge interaction [J]. KSCE Journal of Civil Engineering, 2015, 19(1):220-232．

[8] 孟阳君,周先雁.车辆荷载作用下大跨旧桥动力可靠度研究[J].振动与冲击,2013,32(11): 155-160． MENG Yang-jun, ZHOU Xian-yan. A long-span old bridge’s dynamic reliability under vehicular load [J]. Journal of Vibration and Shock, 2013, 32(11):155-160．

[9] 贾布裕, 余晓琳, 颜全胜, 等. 基于 Kriging 改进响应面法的桥梁地震动力可靠度研究[J]. 振动与冲击, 2013, 32(16): 82-87． JIA Bu-yu, YU Xiao-lin, YAN Quan-sheng, et al.. Bridge seismic reliability analysis based on improved Kriging response surface method [J]. Journal of Vibration and Shock, 2013, 32(16): 82-87．

[10] HAN W, YUAN S, MA L. Vibration of vehicle-bridge coupling system with measured correlated road surface roughness [J]. Structural Engineering and Mechanics, 2014, 51(2): 315-331．

[11] 鲁乃唯, 刘扬, 邓扬. 随机车流作用下悬索桥钢桥面板疲劳损伤与寿命评估[J]. 中南大学学报：自然科学版, 2015, 46(11): 4300-4306． LU Nai-wei, LIU Yang, DENG Yang. Fatigue damage and life assessment for steel decks of suspension bridge under stochastic traffic flow[J]. Journal of Central South University: Science and Technology, 2015, 46(11): 4300-4306．

[12] 宗周红,李峰峰,夏叶飞,等.基于 WIM 的新沂河大桥车辆荷载模型研究[J]. 桥梁建设, 2013, 43(5): 29-36． ZONG Zhou-hong, LI Feng-feng, XIAO Ye-fei, et al.. Study of vehicle load models for Xinyi river bridge based on WIM data [J]. Bridge Construction, 2013,43(5): 29-36．

[13] CHEN S R, WU J. Modeling stochastic live load for long-span bridge based on microscopic traffic flow simulation [J]. Computers and Structures, 2011, 89(9): 813-824．

[14] 韩万水,武隽,马麟,等.基于微观交通流模型的风-车-桥系统高真实度模拟[J].中国公路学报,2015,28(11): 37-45． HAN Wan-shui. WU Jun, MA Lin, et al. High-fidelity simulation of wind-vehicle-bridge system based on microscopic traffic flow model [J]. China Journal of Highway and Transport, 2015, 28(11): 37-45．

[15] LIU N, GAO W, SONG C, et al. Interval dynamic response analysis of vehicle-bridge interaction system with uncertainty [J]. Journal of Sound and Vibration, 2013, 332(13): 3218-3231．

[16] CHEN S, CAI C. Equivalent wheel load approach for slender cable-stayed bridge fatigue assessment under traffic and wind: feasibility study[ J]. Journal of Bridge Engineering, 2007, 12(6): 755-764．

[17] GHAZIZADEH S, BARBATO M, TUBALDI E. New analytical solution of the first-passage reliability problem for linear oscillators [J]. Journal of Engineering Mechanics, 2011, 138(6): 695-706．

[18] 沈锐利,官快,房凯.车桥耦合数值模拟桥梁冲击系数随机变量的概率分布[J].振动与冲击, 2015, 34(18): 123-128． SHEN Rui-li, Guan Kuai, FANG Kai. Probability distribution of random variables of impact coefficient in numerical simulation of vehicle-bridge coupled vibration [J]. Journal of Vibration and Shock, 2015, 34(18): 123-128．

[19] 朱劲松,肖汝诚,何立志.大跨度斜拉桥智能可靠度评估方法研究[J].土木工程学报,2007, 40(5): 41-48． ZHU Jin-song, XIAO Ru-cheng, HE Li-zhi. Reliability assessment of large-span cable-stayed bridges based on artificial intelligence [J]. China Civil Engineering Journal, 2007, 40(5): 41-48．

[20] 公路悬索桥设计规范: JTG D65-05[S].北京:中华人民共和国交通运输部, 2015．

Dynamic reliability assessment for long-span bridges under vehicle load

LU Nai-wei1, LUO Yuan2, WANG Qin-yong2, Noori Mohammad1

(1.SchoolofCivilEngineering,SoutheastUniversity,Nanjing210096,China;2.SchoolofCivilandArchitectureEngineering,ChangshaUniversityofScienceandTechnology,Changsha410114,China)

The dynamic reliability of a suspension bridge under three types of stochastic traffic flow loads were analyzed in order to evaluate the serviceability of long-span bridges under traffic flow loads. The stochastic traffic flows were ebtabilished based on the site-specific traffic measurements of a highway. The bridge dynamic responses were calculated by utilizing vehicle-bridge couple vibration approach. In addition, the failure proability was estimated by the first-passage criterition. Finally, the influence of busy traffic flow occupacy ratio on the reliability of the bridge was investigated. Numerical results indicate that the maximum mean value of the dynamic response of girder is in the mid-span point of the suspension bridge, while that of the root-mean square is in the quarter-span point; the serviceability reliability of the long-span bridge in service, Which is caused by up-crossing failure of displacement, is associated with the occupancy ratio of busy traffic flows. The stochastic traffic flow load model is appropriate for probabilistic modeling of the dynamic responses of long-span bridges, since the statistics of traffic flows are involved in the load model. Furthermore, the stochastic traffic flow load model has a potential feasibility for dynamic reliability assessment for long-span bridges.

dynamic reliability; stochastic traffic flow; suspension bridge; weigh-in-motion first-passage; root-mean-square; vehicle-bridge couple vibration

2015-11-17.

中国博士后科学基金资助项目(2015M580383)；江苏省博士后科研基金资助项目(1501045B)；东南大学博士后创新人才培养资助项目.

鲁乃唯(1987—),男,博士后,从事桥梁结构可靠度评估研究. ORCID: 0000-0003-3812-0385. E-mail: lunaiweide@163.com

10.3785/j-.issn.1008-973X.2016.12.012

U 448.25

A

1008-973X(2016)12-2328-08