关注六大热学问题 科学备考选修3—3
2016-12-15李胜强
李胜强


关注问题一: 热力学系统的研究对象
分子动理论的内容:物质是由大量分子组成,分子做永不停息的无规则运动,分子间同时存在着相互作用的引力和斥力.分子动理论是热学的基础,其内容表明:①分子很小(分子直径的数量级10-10 m, 分子体积的数量级10-30 m3, 分子质量的数量级10-26 kg), ②分子很多(NA=6.02×1023 mol-1 ),③分子的运动永不停息(扩散现象和布朗运动),④分子间同时存在着相互作用的引力和斥力(固体和液体难压缩).
两分子间作用力表现为引力还是斥力,取决于两分子间的间距.当两分子间的间距r>10-10 m时,两分子间作用力表现为引力(此时引力大于斥力),随着间距的减小,引力做正功,分子势能逐渐减小;当两分子间的间距r<10-10 m时,两分子间作用力表现为斥力(此时斥力大于引力),随着间距的减小,斥力做负功,分子势能逐渐增大;故r=10-10 m处,两分子间作用力为零,分子势能最大且为负值.当两分子间的间距r>10-9 m时,两分子间作用力表现为零(此时斥力和引力均为零);
扩散现象和布朗运动的研究对象不同,扩散现象的研究对象是分子(固体分子,液体分子或气体分子),它表明了:①分子间有间隙,②分子的运动永不停息(能彼此进入对方).布朗运动的研究对象是布朗粒子(可以是小碳粒也可以是花粉颗粒),是在显微镜下观察到的无规则运动,布朗运动间接反映了与布朗粒子接触的液体分子或气体分子的无规则运动.
表面张力的研究对象是液体与空气接触的表面层,液体表面层与液体内部相比,表面层分子分布较为稀疏,分子间距离r>r0,分子间作用力表现为引力,它的作用是使液体表面具有收缩的趋势.
浸润和不浸润现象的研究对象是液体与固体接触形成的附着层,当附着层的液体分子比液体内部分子稀疏时,附着层的液体分子间作用力表现为引力,附着层有收缩的趋势,此时液体和固体间表现为不浸润;当附着层的液体分子比液体内部分子稠密时,附着层的液体分子间作用力表现为斥力,附着层有扩展的趋势,此时液体和固体间表现为浸润.
关注问题二:热力学系统的核心规律
理想气体的状态方程是热力学系统的核心规律之一,其表达式为:PVT=C=nR,其中常量C是与理想气体的压强P、温度T和体积V均无关的常量,其适用条件是理想气体和温度不太低、压强不太大的实际气体.由理想气体的状态方程可得出玻意耳定律:PV=C1=nRT;查理定律:PT=C2=nRV;盖-吕萨克定律:VT=C3=nRP,其中常量C1、C2、C3是与压强P、温度T和体积V有一定关系的常量,该常量又与等温线、等容线、等压线息息相关,善于利用控制变量和数形结合的物理思想解决问题.
热力学系统的另一核心规律是热力学第一定律,这也是能量守恒定律在热力学系统的具体应用,其表达式为:ΔU=Q+W,该公式表明了改变物体内能的两种方式——做功和热传递.当外界对热力学系统做功,同时热力学系统又从外界吸收热量,热力学系统的内能增大;当热力学系统对外界做功,同时又对外界放出热量,热力学系统的内能减小;当外界对热力学系统做功,同时热力学系统又对外界放出热量,热力学系统的内能可能增大、可能减小、可能不变.
关注问题三: 热力学系统的力学分析
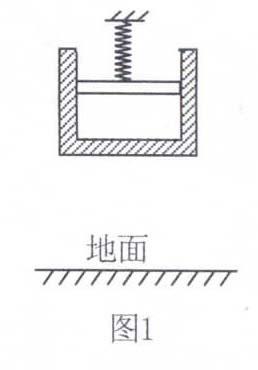
例1 如图1所示,内壁光滑的汽缸被一根竖直轻弹簧悬吊在空中静止不动,缸壁导热性良好,外界气温保持不变.若外界大气压缓慢增大,下列说法正确的是
A.弹簧将缩短一些
B.缸内气体压强变大
C.汽缸底部到地面的距离将增大
D.汽缸内单位体积的气体分子数增加,气体对外界做功
解析 以汽缸为研究对象,外界大气压缓慢增大,缸内气体压强也缓慢增大,故B项正确;以汽缸和活塞整体为研究对象,外界大气压缓慢增大,不影响弹簧的伸长状态,弹簧的长度保持不变,活塞的位置也不变,故A项错误;以封闭气体为研究对象,缸壁导热性良好,外界气温保持不变,故封闭气体的温度不变,缸内气体压强缓慢增大时,封闭气体的体积缓慢减小,活塞的位置不动,汽缸逐渐向上缓慢移动,故C项正确;封闭气体体积体积缓慢减小时,汽缸内单位体积的气体分子数增加,外界对气体做正功,气体对外界做负功,故D项错误.
答案:B、C
拓展1 汽缸和活塞都是由绝热材料制成,若外界大气压缓慢增大,则缸内气体压强也缓慢增大,缸内气体体积逐渐减小,弹簧的长度保持不变,活塞的位置也不变,汽缸逐渐向上缓慢移动,外界对气体做正功,缸内气体内能增大,故缸内气体的温度升高.
拓展2 缸壁导热性良好,外界大气压保持不变,若外界气温缓慢增大,则缸内气体压强也保持不变,缸内气体体积逐渐增大,弹簧的长度保持不变,活塞的位置也不变,汽缸逐渐向下缓慢移动,外界对气体做负功,缸内气体内能不变,故缸内气体从外界吸热.
关注问题四: 热力学系统的过程分析
例2 如图2所示,水平放置的汽缸内壁光滑,活塞厚度不计,在A、B两处设有限制装置,使活塞只能在A、B之间运动,B左面汽缸的容积为V0,A、B之间的容积为0.1V0.开始时活塞在B处,缸内气体的压强为0.9P0(P0为大气压强),温度为297 K,现缓慢加热汽缸内气体,直至399.3 K.求:
(1)活塞刚离开B处时的温度TB;
(2)缸内气体最后的压强P;
解析 缸内气体的压强为0.9P0(P0为大气压强),这表明在B处活塞与限制装置有弹力,现缓慢加热汽缸内气体,故气体先做等容变化(P∝T),当气体压强增大到P0后活塞缓慢向右移动,气体再做等压变化(V∝T),当气体体积增大到1.1V0后,气体再做等容变化(P∝T),直至399.3 K.第一阶段(等容变化):0.9P0297=P0TB,解得:BB=330 K;
第二阶段(等压变化):V0TB=1.1V0TB′,解得:TB′=363 k;第三阶段(等容变化):P0363=P399.3,解得:P=1.1P0.
答案:TB=330 K, P=1.1P0
点拨 “在A、B两处设有限制装置,使活塞只能在A、B之间运动”这句话是本题的关键,应正确理解.在A、B之间运动应理解为缓慢的等压膨胀模型,离开B之前和到达A之后应理解为缓慢的等容升温升压模型,分清楚气体的状态参量的变化情况,本题便迎刃而解.
拓展 为了更形象直观的描述气体的状态参量的变化情况,本题可借助图象,构建P-V图象如图3所示.
关注问题五: 热力学系统的图象问题
例3 一定质量的理想气体从状态A开始经历了ABCDA的循环过程,其V-T图象如图4所示.已知气体在状态A时的压强PA=2×105Pa.试求:
(1)气体在状态B的压强PB;
(2)气体在状态D的温度TD;
(3)完成一个循环,气体与外界热交换的热量Q.
解析 (1) 气体由A到B发生等容变化,有PATA=PBTB, 代入数据解得PB=4×105Pa.
(2)气体由D到A发生等压变化,有
VATA=VDTD,代入数据解得 TB=400K. (3)气体由A到B和由C到D的过程是等容变化,外界不对气体做功.
气体由B到C过程是等压膨胀,气体对外界做功WBC =PB(VC-VB)=4×105×3×10-3 =1200J,气体由D到A过程是等压压缩,外界对气体做功WDA =PA(VD-VA) =2×105×3×10-3 =600J.
从而整个循环过程中,气体对外界做功W总=WBC -WDA =600J,气体经一个循环过程,内能不变,即
ΔU=0, 由热力学第一定律有 Q=W总=600J,即气体从外界吸热600J
答案:PB=4×105Pa;TB=400K;吸热600J
关注问题六: 热力学系统的动态问题
例4 如图5所示,两端开口的U形管,右侧直管中有一部分空气被一段水银柱与外界隔开,若在左管中再注入一些水银(左右两管中水银均未漏出),平衡后则A.两侧水银面A、B高度差h减小
B.两侧水银面A、B高度差h增大
C.右侧封闭气柱体积变小
D.水银面A、B高度差h不变
解析 右侧直管中的空气为研究对象,其压强P=P0+Phc =P0+Ph,即C部分的水银柱的高度始终等于h,在左管中再注入一些水银后,右侧直管中的空气的压强仍保持不变,右侧封闭气柱体积和温度都不变,通过动态调节后水银面A、B高度差h不变.
答案:D
拓展 若将原题中“在左管中再注入一些水银”改为“在右管中再注入一些水银”, 右侧直管中的空气为研究对象,其压强P=P0+Phc ,右侧直管中的空气的温度不变,压强增大,体积减小,两侧水银面A、B高度差h将增大,故选B、C.
