方差分析在仪器比对试验中的应用
2016-12-15徐浩雷湘彭辉
徐 浩 雷 湘 彭 辉
(1.长江委水文局长江上游水环境监测中心, 重庆 400020;2.重庆水务集团股份有限公司排水检测站, 重庆 400063 )
方差分析在仪器比对试验中的应用
徐 浩1雷 湘2彭 辉1
(1.长江委水文局长江上游水环境监测中心, 重庆 400020;2.重庆水务集团股份有限公司排水检测站, 重庆 400063 )
为验证密码质控样在不同仪器上的测定结果是否存在显著性差异,采用3种不同品牌和型号的仪器,连续10 d对同一密码质控样进行测定,利用方差分析方法对测定结果进行处理。结果表明,采用不同仪器和测定方法带来的影响小于仪器本身的重复性影响。因此,利用方差分析方法的处理结果,在协助了解仪器性能状况的同时,对仪器分析结果准确性也有一定的校正作用。
仪器;测定;方差分析;比对试验
1 方差分析概述
1.1 定 义
方差分析是分析一种或多种因素的改变对试验或抽样的结果有无显著性影响的数理统计方法,通过对两组或多组测量数据资料的总体方差是否相同进行推断,检验两个或多个样本方差是否有显著性差异,由于其统计量以F命名,故方差分析也称F检验。如果在试验中只有一个变化因素,那么对应的方差分析称为单因素方差分析;若有多个变化的因素,则称多因素方差分析[1]。
经过多次测量所得的同一样本数据存在差异,产生波动的来源主要有随机波动和因素影响两个方面。前者可看作是随机误差,反映试验结果的精密度;后者可作为系统误差,反映测定条件对结果的影响,确定因素效应。
1.2 方法简介
数据间的差异可通过样本的总离差平方和(总体方差)来反映,若设有m个随机变量x1,x2,…,xm,各变量的样本容量数为ni,则m个变量的总离差平方和QT定义为
(1)
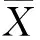
(2)
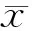
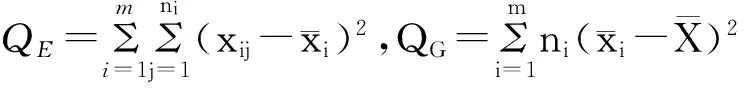
将QT分解为QE、QG两个部分,称QE为组内离差平方和,反映出同一样本内各测定值之间的差异,代表随机误差的影响;称QG为组间内离差平方和,反映出不同因素对样本波动的影响。
在分解的基础上,方差分析借助统计量F来研究各因素对于总离差平方和的影响,统计量F的定义为
(3)
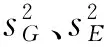
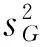
1.3 一般步骤
(1) 提出原假设H0(m个总体有共同的方差和共同的平均值)和备择假设H1(各总体的平均值不全部相等);
(2) 根据样本测量数据,计算各组内、组间方差及自由度的估计值,确定统计量F;
(3) 选定显著性水平α,由F分布表确定在自由度fG和fE下的临界值Fα;
(4) 将F与Fα(fG,fE)比较,若F
2 仪器比对试验
比对试验是设置2个及以上的试验组别,通过对比测结果的比较分析,用以探究各种因素与试验对象的关系。仪器比对是采用不同的检测仪器,由同一操作人员,在相同的试验环境、同一时间段内对同一样品进行测试。
密码质控样作为实验室常用的质量控制手段,其测定结果的准确性对于校准分析仪器、评价分析方法的准确度、监视和校正基线漂移等方面均具有十分重要的意义。原子吸收分光光度法和电感耦合等离子体发射光谱法是目前水中金属含量测定的常用分析方法,对应的原子吸收分光光度计和电感耦合等离子体发射光谱法是目前大多数水环境监测实验室常备的仪器。该试验采用不同的重金属检测仪器,对密码质控样浓度进行测定,旨在观察不同型号仪器设备对测定结果的影响,以验证密码质控样的考核方式是否适用于实验室内各种仪器的测定。
3 实例分析
3.1 主要仪器及试剂
主要仪器有以下3种:①原子吸收分光光度计(AA 800、美国PerkinElmer公司);②原子吸收分光光度计(ICE 3500、美国Thermo Fisher Scientific公司);③电感耦合等离子体发射光谱仪(iCAP 6300、美国Thermo Fisher Scientific公司)。
试剂情况如下:Zn标贮备液1.000 g/L;称取1.000 0 g金属Zn于烧杯中,用优级纯硝酸溶解,用纯水稀释定容至1 000 mL,使用时稀释成10.0 mg/L的Zn标准工作溶液。
3.2 标准物质及分析方法
密码质控样采用标准物质水中锌(GBW(E)080196,水利部水环境监测评价中心),取10.00 mL用0.2%硝酸稀释定容至1 000 mL,标准值为 0.460± 0.023 mg/L。原子吸收分光光度计采用《水质 铜、锌、铅、镉的测定 原子吸收分光光度法》(GB/T 7475-1987),ICP采用《生活饮用水标准检验方法 金属指标》(GB/T 5750.6-2006)5.5电感耦合等离子体发射光谱法,分别对密码质控样进行直接上样测定。
3.3 检测结果
使用AA 800型原子吸收分光光度计、ICE 3500型原子吸收分光光度计和iCAP 6300型电感耦合等离子体发射光谱仪进行检测,设置检测波长为213.8 nm,连续10 d对该密码质控样进行测量,取日平均值参与计算(见表1)。
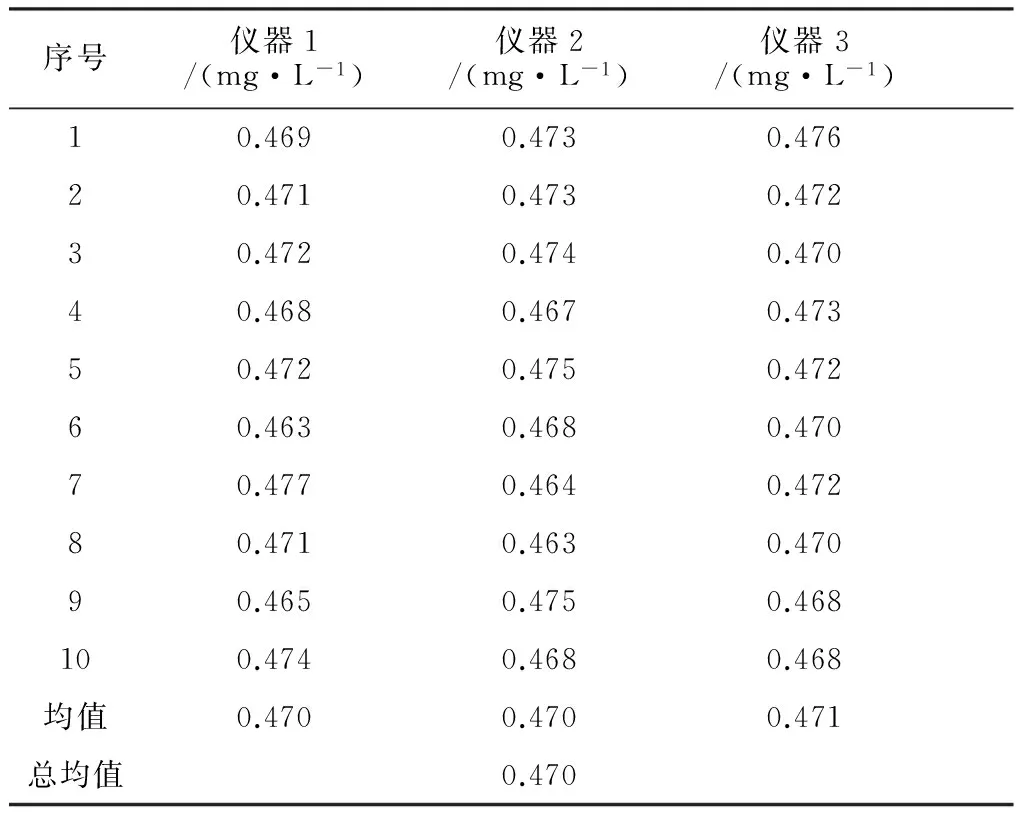
表1 各仪器水中锌含量测定结果
所测数据经准确度检验,均符合密码质控样给定的不确定度范围。
3.4 方差分析
提出原假设H0(不同仪器测定的结果无差异)和备择假设H1(不同仪器测定的结果有差异)。
设定显著性水平α=0.01,对所测的3组数据采用数理统计的单因素方差分析(见表2)。

表2 各仪器测定结果单因素方差分析
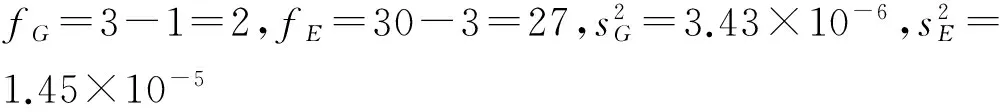
由于统计量F 根据以上数理统计计算及分析结果,可以发现,不同仪器分析测试的结果并无显著性差异,即对于同一批水样,不同品牌的仪器、操作时间的先后顺序、仪器所处的环境等因素,对分析测试的结果并无显著影响。相反,倘若发现在比对试验中出现了F>F临界值的情况,即表明有仪器性能正处于不健康状态,需要检查并找出相关原因。 (1) 方差分析是数理统计中广泛应用的基本方法之一,是科学研究和社会实践中分析数据的重要工具之一。作为仪器对比试验结果检验的方法,操作简便快捷,结论简单明了。 (2) 方差分析显示,测定结果的准确性与采用不同仪器这个因素无关。故采用标准物质检验法对仪器进行测试的结果可信度高,密码质控样作为常用的质量考核方式,不受仪器品牌、型号、所处环境的影响。 (3) 方差分析结果提供了关于各组平均数间差别的总信息,却未提供各组间差别的具体信息,即尚未指出哪几个组平均数间的差别具有或不具有统计学意义,是否存在显著性差别。在实际应用中,影响测量数据结果的因素往往不止一个,在若干因素中,需要确定哪些因素是主要的、各因素间是否有交互作用等问题。为此,需要进行多个样本间的两两比较或进行多因素方差分析[2]。 [1] 杨虎, 钟波, 刘琼荪. 应用数理统计[M]. 北京: 清华大学出版社, 2012. [2] 李锦环. 怎样用方差分析方法分析试验数据[J]. 吉林农业, 2012(2): 60. (编辑:唐湘茜) 2016-09-15 徐浩,男,长江委水文局长江上游水环境监测中心,工程硕士,助理工程师. 测验方法 1006-0081(2016)11-0048-03 TV149 A4 结论及建议
