超级电容储能系统的滑模变结构控制算法研究

郭昊天，戚　栋，苑长富，贾鹏飞

(1.大连理工大学电气工程学院，辽宁大连116023；2.郑州供电公司，河南郑州450006)

超级电容储能系统的滑模变结构控制算法研究

郭昊天1,2，戚栋1，苑长富1，贾鹏飞2

(1.大连理工大学电气工程学院，辽宁大连116023；2.郑州供电公司，河南郑州450006)

针对超级电容储能系统的非线性和输入输出扰动大等问题，基于直流变换器固有的开关特性，分别提出了系统在充、放电状态下的滑模变结构控制方法。在Boost模式下利用非线性系统的微分几何理论，建立反馈精确线性化模型并设计滑模变结构控制器；在Buck模式下以系统控制目标为基础提出分段滑模控制算法。研究结果表明，相比传统PID控制，滑模变结构控制具有更好的动态响应及鲁棒性，在输入端电压或负载大幅度波动的情况下，输出仍能保持恒定和较低的纹波系数，提高了超级电容储能系统的抗干扰能力。

超级电容储能系统；Buck-Boost变换器；非线性；滑模变结构控制

超级电容储能系统通常需要通过双向直流变换器接入主系统的直流母线中，而主系统负载往往随工况大幅变化，这就要求超级电容储能系统必须具备良好的动态响应和鲁棒性[1]。又由于开关通断造成的工作状态不连续，使变换器具有非线性特性。基于以上因素，以线性系统分析为基础的控制算法已无法满足系统需求。

超级电容储能系统目前多采用Buck-Boost直流变换器[2-3]，并以电压和电流为反馈变量建立闭环PI控制算法，但系统抗扰动能力差，控制效果不理想。滑模变结构控制算法由于其滑动模态可以按需要设计，与系统的参数及扰动无关，使该控制方法具有很好的鲁棒性[4]。当滑模面及控制函数选取得当时，系统也具有优良的动静态响应特性，而直流变换器的变结构特性，使其很适合于采用滑模变结构控制。文献[5-11]即针对该方面展开研究并获得了良好的控制效果。

本文基于滑模变结构控制思想，以改善系统的动态响应特性和抗扰动能力为目标，以Boost-Buck变换器的非线性特性为基础，提出超级电容储能系统的滑模变结构控制算法。在Boost模式下建立精确反馈线性化模型，在此基础上设计线性滑模变结构控制器，相比传统以状态变量误差为参考的滑模控制方法，具有更优良的动态品质。在Buck模式下以系统控制目标为前提，提出分段滑模变结构控制算法。利用仿真模型将该控制策略与传统PI控制策略相比较，仿真结果验证了该控制策略的有效性，并表明其具有更好的动态响应特性及鲁棒性。

1　超级电容储能系统结构组成

超级电容储能系统结构如图1所示，由超级电容器、双向Buck-Boost变换器及系统的直流母线端构成。当系统处于轻载或者能量回馈状态时，直流母线电压升高，此时直流母线相当于电源，超级电容为负载，变换器工作于Buck模式给超级电容充电；当系统处于重载时，变换器工作于Boost模式，由超级电容放电为系统补偿能量，稳定直流母线电压。由于系统负载的随机性及超级电容充放电时频繁的电压波动，若要获得良好的控制效果及能量利用效率，就要针对性地提出对于系统的控制策略。

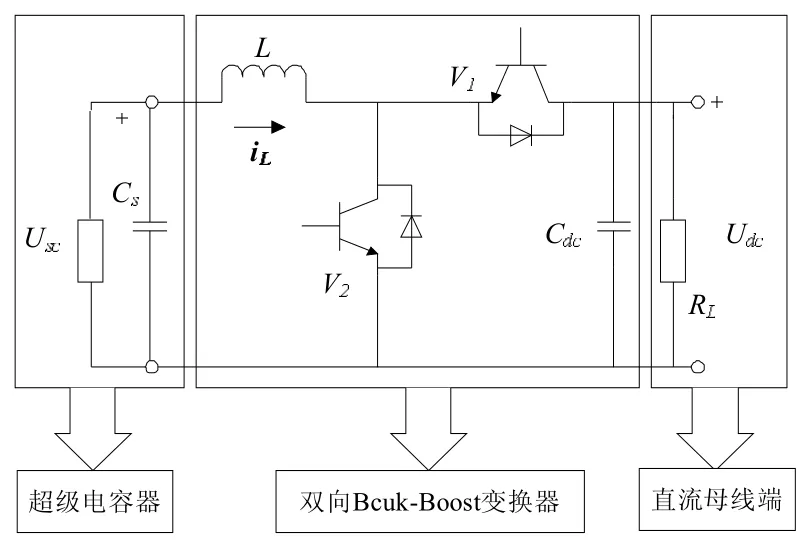
图1　超级电容储能系统基本结构图

2　Boost模式控制算法设计

2.1Boost变换器仿射非线性模型

系统工作于Boost模式下时，V1常开，系统工作状态随V2通断而改变。基于CCM模式分析，定义开关函数如下：

令x1=iL,x2=udc，则由图1得，系统的仿射非线性标准方程为：

2.2Boost变换器精确反馈线性化

对于上述单输入单输出仿射非线性系统，若系统满足非线性系统精确线性化条件，并且通过构建适当的输出函数的h(x)，则可以得到以z1、z2为状态变量的系统线性方程[12]。经验证可知系统满足非线性系统精确线性化条件。

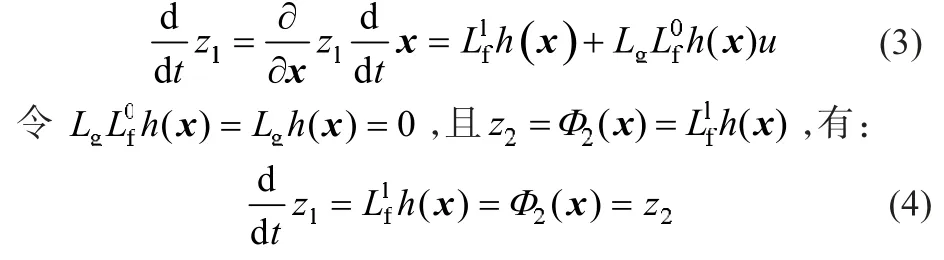
类似的有：

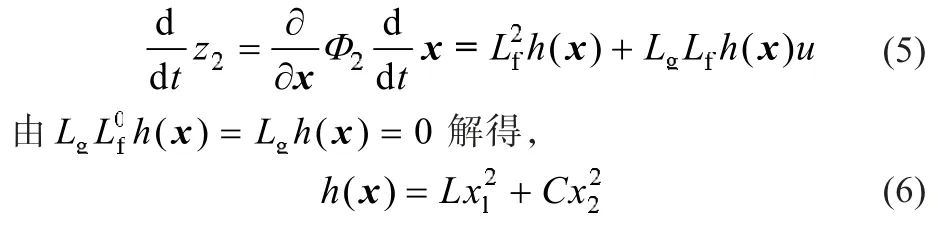
于是得状态变换为:

式中：v为新的控制变量，与u的关系由式(5)给出。

2.3滑模变结构控制器设计

通过状态反馈和微分同胚变换，将原非线性系统的全局输出调节问题，转化为线性系统对非线性系统的跟踪问题，线性系统中对于系统平衡点z0的跟踪与非线性系统中对于x0的跟踪是等价的。由此可建立线性滑模函数，以线性滑动模态求解其控制策略[13]。选用线性切换函数：

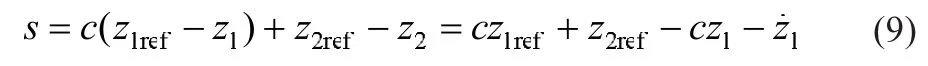
式中：z1ref,z2ref为系统处于稳态工作点时z1，z2的值，其值与x1ref，x2ref关系由式(7)可得，其中，

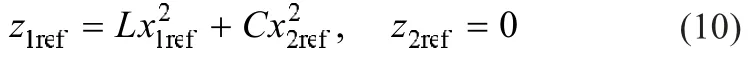
在状态空间中，滑模运动由一个一阶线性微分方程确定，其特征方程为p+c=0。

由特征方程可知，当c＞0，该特征方程的根在左半平面，即得渐进稳定的滑模运动，保证了滑模运动的稳定性。c的整定，可根据仿真或实验结果进行调整。

由式(5)得：

将式(12)代入式(11)中，并求取满足广义滑模条件的切换函数，由于Boost变换器为控制受限系统，u只能在{0，1}中取值，经验证在此选取u=0.5[1+sign(s)]即可满足条件。

利用坐标反变换，可得原系统对应切换函数：

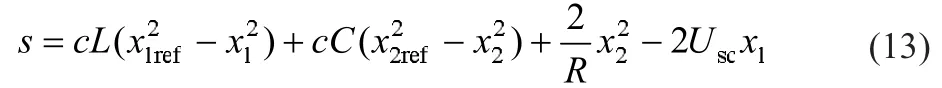
3　Buck模式控制算法设计

3.1Buck变换器仿射非线性模型

与Boost分析类似，在此令x1=iL，x2=usc，则Buck模式状态方程为：

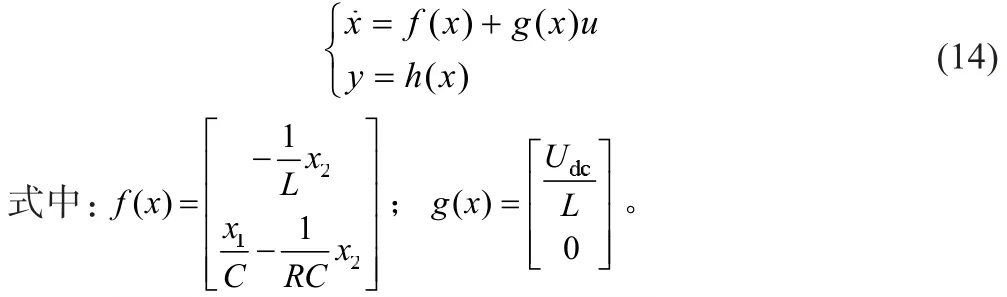
由于在为超级电容储能系统充电时的控制目标是分阶段的，即当超级电容电压远小于额定电压时采用恒流充电；当电容电压接近于额定电压时采取涓流恒压充电，故分别选取电感电流iL和电容电压Usc为反馈控制变量建立滑模变结构控制，并设定滞环比较器防止系统频繁在两种控制算法之间进行切换。

3.2恒流充电状态滑模控制设计

当系统工作于恒流充电模式时，由于iL导数不连续，故只能构造单滑模面方程：s=x1－ir，其中：ir为恒流充电时电流参考值。

根据李导数形式表达的到达条件：

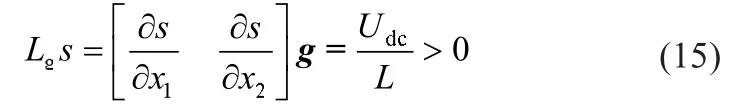
Buck变换器为控制受限的系统，u只能在 {0，1}之中取值，为满足横截条件，取u=0.5[1+sign(s)]，令ds/dt=0，求取等效控制：

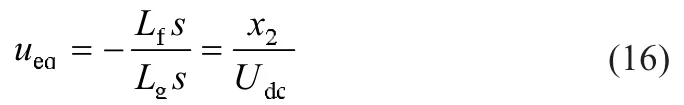
由于Buck变换器输出电压始终小于输入电压且极性相同，故0＜ueq＜1，满足横截条件和滑模存在条件。

3.3恒压涓流充电状态滑模控制设计

系统工作于恒压模式时，构造滑模切换函数：

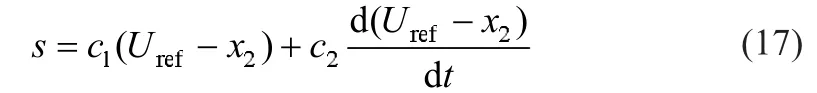
式中：Uref为超级电容电压参考输入；c1，c2是设计参数。

到达条件计算为：

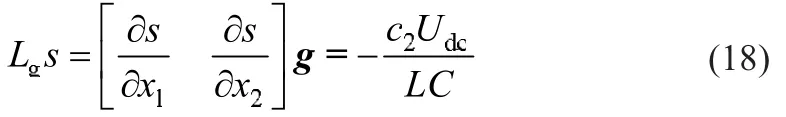
在此选取u=0.5[1+sign(s)]，则为满足横截条件，有c2＞0。继而求取等效控制：

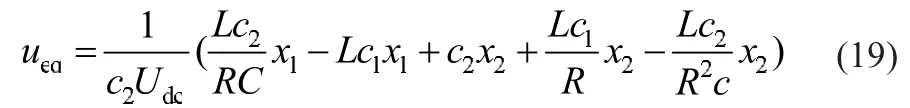
由于等效控制时有s=0，由此推导出:

将式(20)代入式(19)，得:

若系统渐进稳定，则0＜ueq＜1,观察式 (21)可知，若令c1=1/RC，c2=1，则ueq满足约束条件，于是构造的滑模切换函数为：

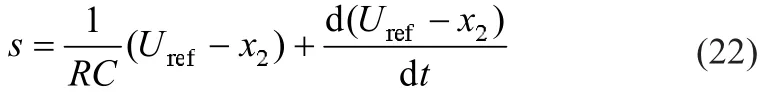
4　滑模变结构控制性能验证

4.1仿真参数

在Matlab/Simulink中对超级电容储能系统控制算法进行验证，仿真各部分参数为：Buck-Boost双向变换器电感L= 15 mH，IGBT开关频率f=10 kHz，直流母线侧额定电压Udc=200 V，滤波电容C1=1 000 μF，负载电阻R=3 Ω，超级电容C=7.9 F，额定电压Usc=100 V。系统充放电电流需根据运行功率计算，在此取放电电流参考值为i1ref=70 A，充电电流i2ref=50 A。

4.2响应特性分析

4.2.1Boost模式下启动响应特性

设定系统处于重载状态，启动超级电容储能系统为直流母线供电，维持直流母线电压恒定。由图2知，两种控制方法在启动过程中均存在一定超调，但滑模变结构响应时间短，无振荡周期，电感电流和输出电压分别经过8和20 ms后即进入稳态，而传统PI控制响应时间较长，电感电流和输出电压在经过两个振荡周期后才进入稳态。由此说明相比传统PI控制，滑模变结构控制具有更优越的动态响应特性。

图2　Boost模式启动响应特性比较

4.2.2Buck模式下启动响应特性

设定系统处于能量回馈状态以恒流充电方式为超级电容充电。由图3可知，滑模变结构控制无超调、无振荡，充电电流在经过6 ms左右的响应时间后即进入稳态，而传统PI控制有10%左右超调，在经过两个振荡周期之后于50 ms左右才进入稳态。

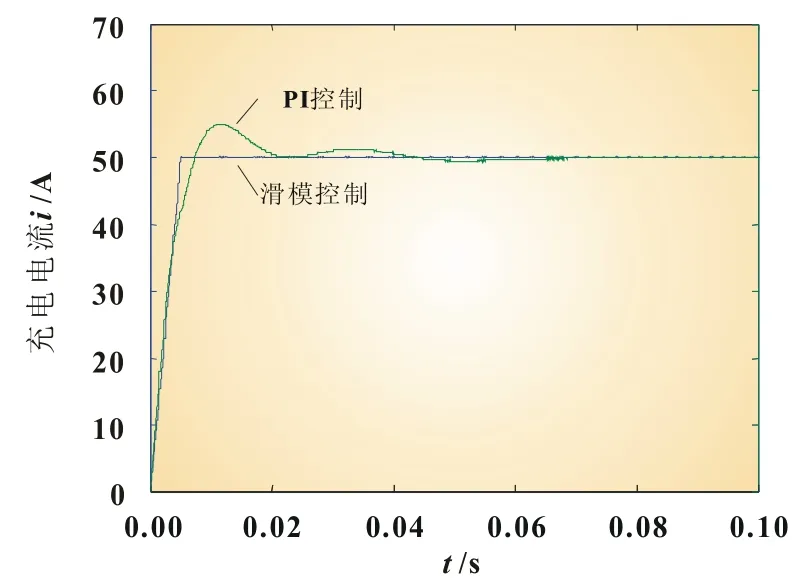
图3　Buck模式启动响应特性比较

4.2.3Boost 模式负载扰动特性

如图4 所示，系统处于充电状态时负载电阻从5 Ω 跳变到3 Ω，之后又恢复至5 Ω，由图可以看出，相比PI 控制，滑模变结构控制在扰动发生后能更迅速的响应，调节时间短，超调小，波形畸变率低，由此说明滑模变结构控制对于维持直流母线的稳定具有更好的控制效果。

图4　负载扰动下Boost模式动态响应比较

4.2.4Buck模式输入电压扰动特性

如图5所示，系统处于放电状态时直流母线电压从200 V跳变至230 V，之后又恢复正常。由图可以看出，滑模变结构控制下的充电电流波形在扰动发生后几乎无变化，而PI控制则有一定的超调，且过渡时间缓慢。由此说明滑模变结构控制能够维持系统充电时电流的恒定。

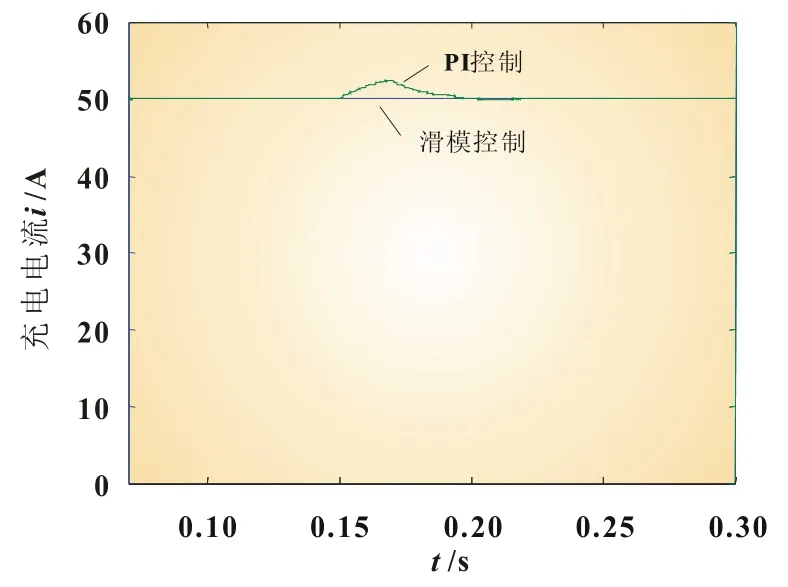
图5　输入电压扰动下Buck模式动态响应比较

4.2.5Buck模式切换工作状态动态响应特性

当系统从恒流充电状态向恒压涓流状态过渡时，系统的控制目标从电流转为电压，控制策略相应发生改变。由图6看出，当超级电容电压接近于额定电压时，电流迅速下降然后缓慢趋于0 A，电容电压平缓过渡至额定值，最终都达到稳定状态且并无稳态误差。由此表明分段滑模变结构控制具有期望的控制效果，具有良好的动稳态特性。

图6　Buck模式工作状态切换动态响应特性

5　结论

本文针对超级电容储能系统的非线性和输入输出扰动大的特点，采用滑模变结构控制以保证系统具有良好的鲁棒性。在Boost模式下将精确线性化理论与滑模变结构控制相结合，在经状态变换后的线性系统下设计滑模切换函数，获得了良好的动态品质；在Buck模式下考虑系统不同阶段控制目标不同，提出了分段滑模变结构控制方法，其控制效果符合系统需求。与传统PI控制相比，滑模变结构控制具有更优越的动态响应特性及鲁棒性，提高了超级电容储能系统的抗干扰能力。

[1]KHALIGH A,LI Z.Battery，ultracapacitor，fuel cell，and hybrid energy storage systems for electric，hybrid electric，fuel cell，and plug-in hybrid electric vehicles：State of the art[J].Vehicular Technology，IEEE Transactions on，2010，59(6)：2806-2814.

[2]DISHNER B W.Boost/Buck DC/DC converter:US,Patent 4801-859[P].1989-01-31.

[3]DIXON J W，ORTUZAR M E.Ultracapacitors+DC-DC converters in regenerative braking system[J].Aerospace and Electronic Systems Magazine，IEEE，2002，17(8):16-21.

[4]王丰尧.滑模变结构控制[M].北京：机械工业出版社，1995：188-242.

[5]SIRA-RAMÍREZ H，LUVIANO-JUÁREZ A.Robust input-output sliding mode control of the Buck converter[J].Control Engineering Practice，2013，21(5):671-678.

[6]乐江源，谢云祥，洪庆祖，等.Boost变换器精确反馈线性化滑模变结构控制[J].中国电机工程学报，2011，31(30)：16-23.

[7]SOSA J L，CASTILLA M，MIRET J，et al.Sliding-mode input-output linearization controller for the DC/DC ZVS CLL-T resonant converter[J].Industrial Electronics，IEEE Transac-tions on，2012,59 (3):1554-1564.

[8]CID-PASTOR A，MARTINEZ-SALAMERO L，EL AROUDI A，et al.Synthesis of loss-free resistors based on sliding-mode control and its applications in power processing[J].Control Engineering Practice，2013，21(5)：689-699.

[9]SIRA-RAMÍREZ H，LUVIANO-JUÁREZ A，CORTÉS-ROMERO J.Robust input-output sliding mode control of the Buck converter [J].Control Engineering Practice，2013，21(5)：671-678.

[10]LÓPEZ-SANTOS O,MARTÍNEZ-SALAMERO L,GARCÉA G, et al.Efficiency analysis of a sliding-mode controlled quadratic Boost converter[J].IET Power Electronics，2013，6(2):364-373.

[11]WAI R J，SHIH L C.Design of voltage tracking control for DC-DC Boost converter via total sliding-mode technique[J].Industrial Electronics，IEEE Transactions on，2011，58(6):2502-2511.

[12]康惠骏.非线性系统理论[M].北京：机械工业出版社，2010：87-108.

[13]邓卫华，张波，胡宗波，等.CCM Buck变换器的状态反馈精确线性化的非线性解耦控制研究[J].中国电机工程学报，2004，24 (5)：120-125.

Research of sliding mode control strategy in supercapacitor-based energy storage system

GUO Hao-tian1,2,QI Dong1,YUAN Chang-fu1,JIA Peng-fei2
(1.School of Electrical Engineering,Dalian University of Technology,Dalian Liaoning 116023,China; 2.Zhengzhou Power Supply Company,Zhengzhou Henan 450006,China)

The sliding mode control methods of charging and discharging system were proposed based on the inherent switching characteristics of DC-DC converters,considering that the supercapacitor energy storage system has large input-output perturbations and system nonlinear problems.Two resolutions were proposed:in Boost mode, the differential geometry of nonlinear systems were adopted,and the state feedback precise linearization scheme and the sliding mode controller were designed;in Buck mode,the segmentation sliding mode control algorithm was adopted to control the target system.The results show that,compared to traditional PID control,sliding mode control has better dynamic response and robustness.The output remains constant and low ripple coefficient with the input voltage or load volatile and it improves the anti-jamming capability of supercapacitor energy storage system.

supercapacitor energy storage system;Buck-Boost converter;nonlinear;sliding mode control

TM 53

A

1002-087 X(2016)10-2026-04

2016-03-16

国家自然科学基金(50577075)

郭昊天(1988—)，男，河南省人，硕士研究生，主要研究方向为超级电容储能，电力电子变换。

戚栋，dlut.qd@263.net