光伏电池建模分析及关键因素研究
2016-12-15赵庆龙曾明华王元良
赵庆龙,曾明华,王元良
(西南交通大学机械工程学院,四川成都610036)
光伏电池建模分析及关键因素研究
赵庆龙,曾明华,王元良
(西南交通大学机械工程学院,四川成都610036)
在传统光伏电池数学模型的基础上,通过合理简化模型,建立了一个结构简单、准确度高的光伏电池模型。借助MATLAB/SIMULINK仿真平台进行建模仿真,模拟不同状态下光伏电池输出特性,通过仿真结果对比分析,验证了模型的工程实用性。对影响光伏电池模型特性的串并联电阻及二极管理想因子等关键因素进行详细对比分析,对光伏电池工程建模仿真有一定的指导意义。
光伏电池;模型简化;仿真分析;影响因素
当今世界节能减排是发展的一个重要目标,光伏产业随之兴起。在光伏电池的实际使用中,由于不同地区间环境的差异性,光伏电池转化效率也不尽相同,因此快速评估一个地区光伏电池的发电效率至关重要。由于一天中光照强度及温度多变,使得光伏电池的出厂参数不能准确反应光伏电池实际效率,所以通过建立一个光伏电池的仿真模型,实时模拟温度及光照强度的变化,能够较好地反应光伏电池的实际输出状态。光伏电池仿真模型的建立通常都是在光伏电池的数学模型下,通过一定的模型简化来实现。不同的简化方式影响着光伏电池仿真的准确性。
本文通过反复实验测试,简化模型中不必要参数,加强对关键参数的细化建模,与标准数据对比后再校正相关参数,得到了一个结构简单、仿真结果准确的仿真模型。同时本文也对影响光伏电池模型关键因素进行了对比建模,通过对仿真结果分析,定量反映出关键因素不可忽略的影响,从而在实际应用中能够快速准确地对光伏组件进行仿真评估。
1 光伏电池等效电路
光伏电池的等效电路[1-9]如图1所示,图中PN结由PN结合部和串联电阻RS组成,RS为考虑横向电流的等效电阻;Iph为光电流,由光伏电势产生;Rsh为分路电阻,来补偿由于PN结缺陷造成的漏电流Ish;ID为PN结的正向电流,I为负载电流。
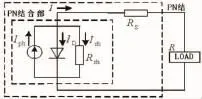
图1 光伏电池等效电路
光伏电池输出电流等效电路方程式为:
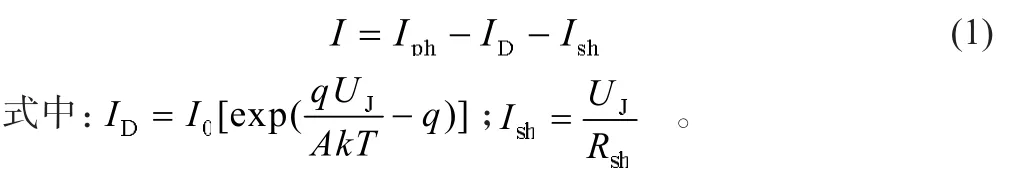
光伏电池电压等效电路方程式为:

式中:UJ为PN结合部端电压;U为负载电压;I为负载电流;RS为负载电阻。
由以上[2]可得光伏电池输出电流方程式:
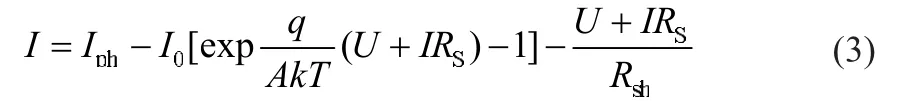
式中:A为PN结材料特性系数;k是波兹曼常数为1.381× 10-23J/K;T为绝对温度;q是电子电量为1.602×10-19C。
2 光伏电池模型简化
由于Rsh较大,通常为千欧级,Ish可以等效为零[3],方程式(3)中的光伏电池输出电流可简化为:
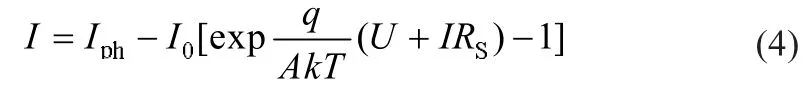
在实际应用中,单个光伏电池很难满足需要,通常按要求将若干个光伏电池串并联,得到所需要的光伏阵列[3],此时输出电流为:
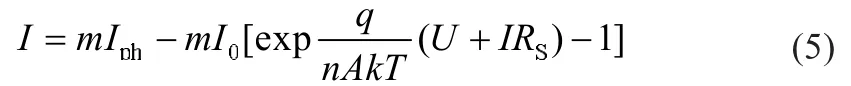
式中:m、n分别为电池并联、串联数。
光生电流Iph与标准状况下的参考短路电流ISCref、温度及光照强度的关系为:
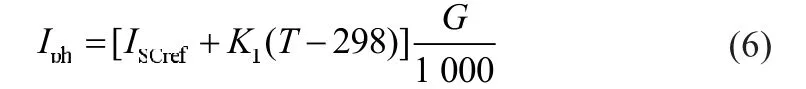
对于光伏电池反向饱和电流,负载开路时I=0,U=UOC,带入上述公式(5)得:
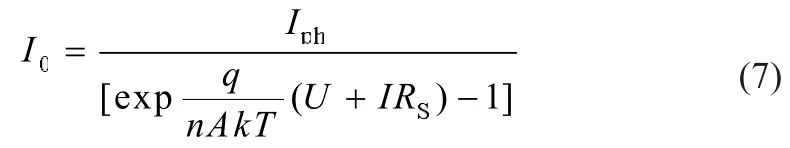
开路电压受光照强度的影响不大,简化只考虑温度的影响[4],其中UOCref为标准状况下的开路电压,为:
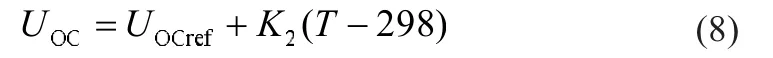
本文中忽略串联等效电阻受温度及外界接线等的影响[3],将其简化为一个定值,通过在最大功率点处的电流Impp与电压Umpp的值来计算,见(9)和(10)。在对大型的工程类光伏系统仿真时,需要对串联等效电阻进行一定的修正,使得仿真模型接近于实际。
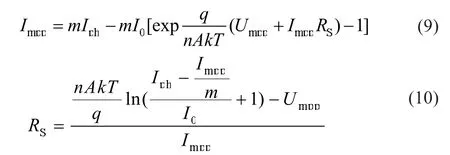
3 光伏电池的建模分析
3.1光伏电池SIMULINK建模
利用简化的光伏电池数学模型,在SIMULINK中进行建模。本文中选用某光伏公司所产235 W光伏板进行建模仿真,根据出厂参数可知,该电池由6×10串联电池片组成,在标准状况下 (AM=1.5,T=25℃,G=1 000 W/㎡),最大工作电流Impp=7.89 A,最大工作电压Umpp=29.8 V,开路电压USCref=37.6 V,短路电流ISCref=8.29 A,开路电压温度系数K1=-0.127 84 V/℃,短路电流温度系数K2=0.004 974 A/℃,经测算后取A=1。
将上述数据带入简化后的数学模型(10)中可得RS= 0.405 6 Ω,将公式(9)在SIMULINK中进行建模仿真,并将公式中的各组成参数分别建模封装,可得到如图2所示仿真模型。将光伏电池的各部分进行进一步封装,得到如图3所示模型。
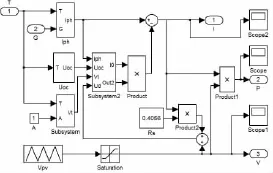
图2 光伏电池仿真模型
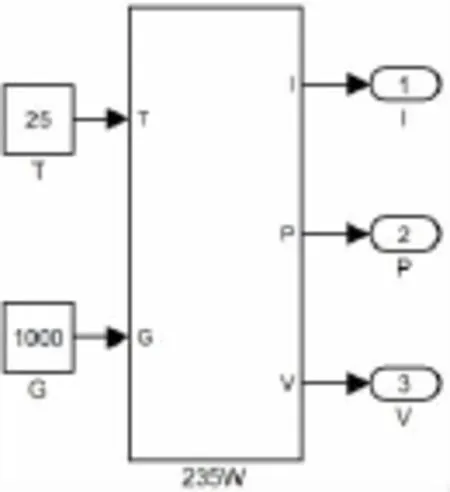
图3 光伏电池封装模型

图4 不同温度下P-U与I-U曲线
3.2光伏电池仿真结果分析与验证
利用SIMULINK中建立的光伏电池模型,通过分别模拟在不同温度及光照强度下进行仿真,可以得到如图4所示的仿真曲线。
图4中,在G=1 000 W/㎡的标准光照强度下,改变温度,得到温度对光伏电池输出功率及输出电流的影响。可以看出温度越高,光伏电池的最大功率点越低,光伏电池的整体输出功率下降,开路电压也越小,短路电流越小。不同温度下输出电流在负载电压较小时变化不大,在负载电压接近开路电压时,输出电流开始不同程度的下降。
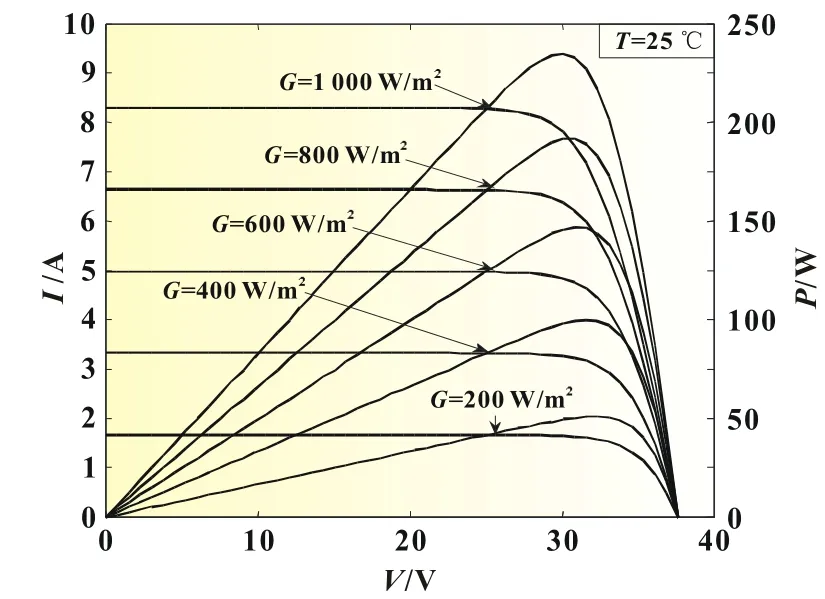
图5 不同光照强度下P-U与I-U曲线
图5中,在T=25℃的标准温度下,改变光照强度,得到光照强度对光伏电池输出电流及输出功率的影响,可以看出光照强度越强,光伏电池的最大功率点越高,光伏电池的整体输出功率也越大,短路电流和输出电流也越大。
由图4和图5可以看出光伏电池在一定温度和日照强度下具有唯一的最大功率点,但光伏电池是一个非线性电源[2],输出特性受温度和日照强度影响较大,使得输出电流和电压变化较大,输出功率不稳定,这也使得最大功率点发生变化,导致太阳电池效率降低。
为了验证所建光伏电池模型的实用性,将光伏电池厂商数据与仿真数据进行P-U特性曲线对比[5,8]。由图6和图7可以看出本文所建光伏电池模型的输出功率与厂商提供的输出功率偏差较小,在合理的误差范围内,具有较强的工程实用性。
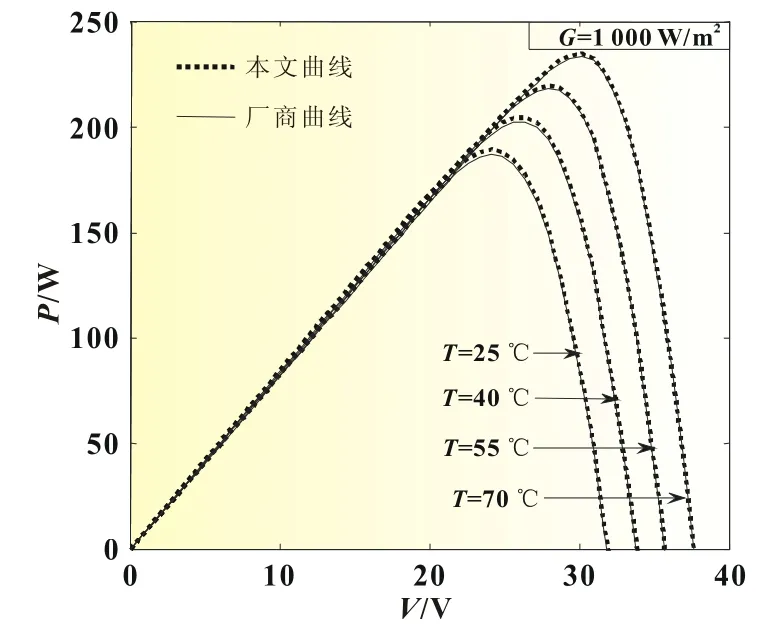
图6 不同温度下P-U对比曲线
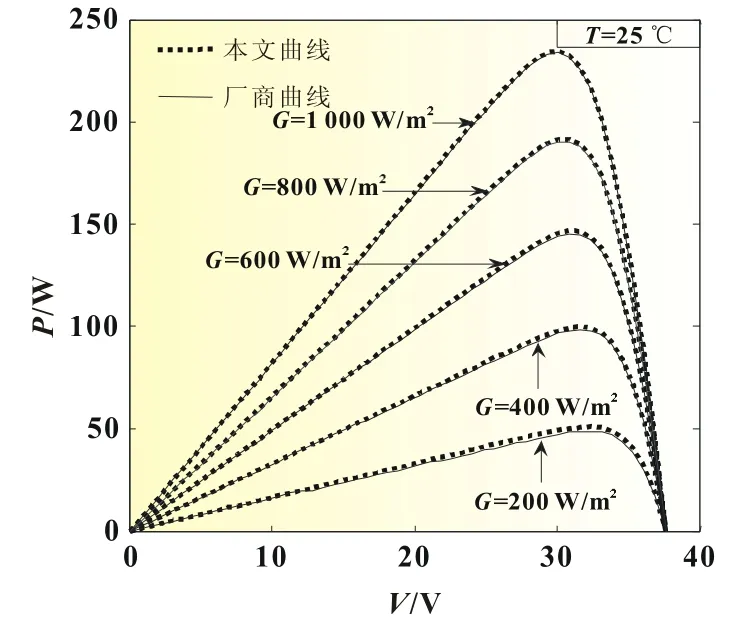
图7 不同光照强度下P-U对比曲线
4 影响光伏电池模型的关键因素
4.1串联等效电阻的影响
通常情况下,串联等效电阻RS被认为是光伏电池板电极及材料本身的电阻。而在光伏电池组建的实际使用中,组件间的接线或组件与电缆连接件的电阻,也应认为是等效电阻的一部分[1],同时也应该考虑串联等效电阻在不同的温度下,以及不同的连接件下电阻值的变化。
在标准状况下(AM=1.5,T=25℃,G=1 000 W/㎡),不计外加电阻及温度变化影响时,等效电阻RS为0.405 6 Ω。当改变等效电阻值时,光伏电池输出特性曲线如图8和图9所示。
由图8可以看出,在当负载电压较小时,输出电流可认为近似不变,而串联等效电阻越大,对光伏电池的输出电流影响越大,对开路电压几乎没有影响,串联等效电阻达到一定的限制值后,光伏电池输出电流随着负载电压呈近似线性变化,与标准光伏电池I-U曲线不符,由此可见等效串联电阻的值对输出电流有着较大影响。
由图9可以看出串联等效电阻对光伏电池的输出功率影响较大,串联等效电阻越小,光伏电池的功率越大,最大功率点越高,当串联等效电阻变大时,光伏电池输出功率下降,最大功率点也发生了偏移。
由以上仿真结果可以看出等效电阻对光伏电池的输出功率影响较大,不可忽略。这也提醒我们在大型工程建模仿真时,要考虑到实际应用中的附加等效电阻,从而使得模型更加接近实际,仿真的精确度更高,误差更小,实用性更强。
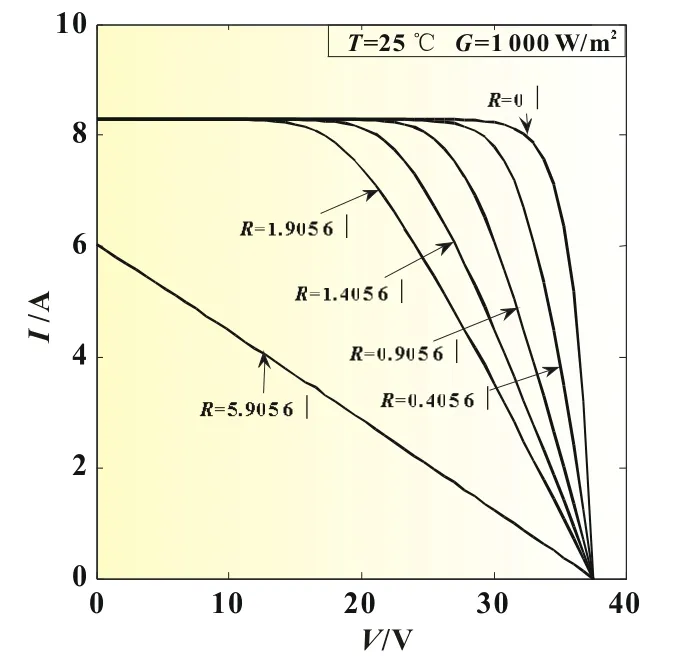
图8 不同串联电阻下I-U曲线
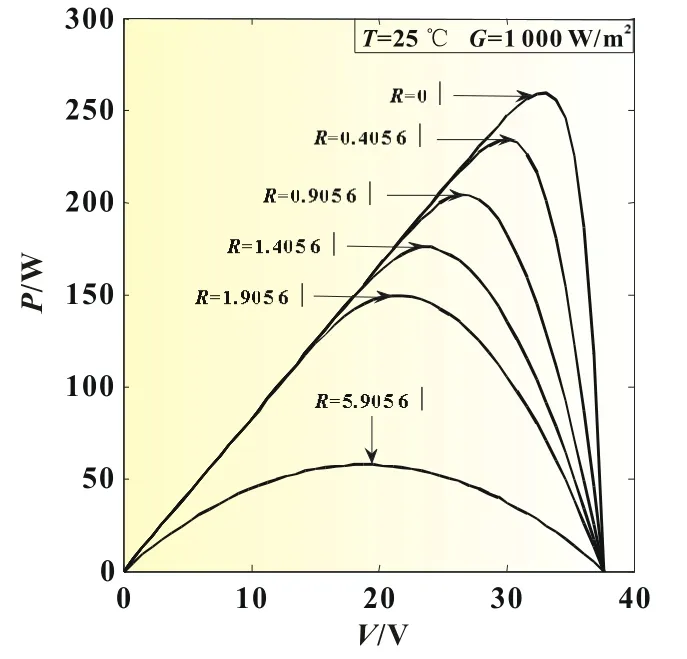
图9 不同串联电阻下P-U曲线
4.2并联分路电阻Rsh的影响
Rsh是PN结生产制造过程中产生的,由相关文献可知Rsh增大会导致开路电压减小,短路电流基本不变[5],对电池的影响不大。又由于Rsh值为千欧级,流过其上电流近似为零,因此在简化的建模中可以不予考虑。
4.3光伏电池等效因子的影响
光伏电池等效因子A是与光伏电池PN结材料特性有关的系数,它的值通常在1~2之间,本文通过参考文献[7]的算法和文献[10]中的估算方法,经测算修正后等效因子A的值取为1。由于不同厂家材料差异性,A的最适匹配值也不同。由图10仿真结果可知,随着A的值增加,一定程度上会引起输出电流的降低,从图11仿真结果可以看到,A的值增加使得光伏电池的输出功率整体下降。因而,需要进行反复测算确定A的值。

图10 不同等效因子下P-U曲线
5 结论
本文通过对光伏电池模型的合理简化,建立了一个结构简单、仿真精度高的模型。通过改变温度及光照强度等参数对光伏电池在不同状态下的输出特性进行了全面的模拟与研究分析。本文还对影响光伏电池模型的关键因素进行了详细分析,通过仿真结果的对比,定量反映出不同因素的影响程度。综合本文的简化模型和影响光伏电池的关键因素,在实际工程建模仿真的应用中,可以快速、准确地建模和评估光伏发电系统的输出功率及效率。
[1]冯垛生,王飞.太阳能光伏发电技术图解指南[M].北京:人民邮电出版社,2011.
[2]周德佳,赵争鸣,吴理博,等.基于仿真模型的太阳能光伏电池阵列特性的分析[J].清华大学学报:自然科学版,2007,47(7):1109-1112.
[3]胡长武,李宝国,王兰梦,等.光伏电池简化数学模型的Matlab/Simulink仿真研究[J].可再生能源,2013,31(10):20-24.
[4]XIAO W,DUNFORD W G,CAPEL A.A novel modeling method for photovoltaic cells[J].35th Annual IEEE Power Electronics Specialists Conference,2004,3:1950-1956.
[5]茆美琴,余世杰,苏建徽,等.带有MPPT功能的光伏阵列Matlab通用仿真模型[J].系统仿真学报,2005,17(5):1248-1251.
[6]马帅旗.太阳能光伏电池建模及V-I特性研究[J].电源技术,2013, 37(8):1396-1398.
[7]孔祥雨,徐永海,曾雅文,等.一种求解光伏电池5参数模型的方法[J].电力系统保护与控制,2013(22):46-50.
[8]侯金明,许鹏.基于四参数模型的光伏阵列Matlab/Simulink仿真模型[J].可再生能源,2013,31(6):10-14.
[9]万晓凤,张燕飞,余运俊,等.光伏电池工程数学模型的比较研究[J].计算机仿真,2014,31(3):113-117.
[10]VILLALVA M G,GAZOLI J R,FILHO E R.Comprehensive approach to modeling and simulation of photovoltaic arrays[J].IEEE Transaction on Power Electronics,2009,24(5):1198-120.
Analysis of photovoltaic cells model and key factors research
ZHAO Qing-long,ZENG Ming-hua,WANG Yuan-liang
(School of Mechanical Engineering,Southwest Jiaotong University,Chengdu Sichuan 610036,China)
Based on the traditional mathematical model of photovoltaic cells,a simple structure and high accuracy photovoltaic cell model was built by simplifying the model reasonably.The output characteristics of photovoltaic cells under different conditions were simulated by using MATLAB/SIMULINK simulation platform,the practicability of model was verified comparing the results of simulation analysis.The key influencing factors of photovoltaic cells model like series and shunt resistance and diode ideality factor were compared and analyzed in detail,which has certain directive significance to the engineering modeling and simulation of photovoltaic cells.
photovoltaic cells;model simplification;simulation;influencing factors
TM 914
A
1002-087 X(2016)10-1969-04
2016-03-24
西南交通大学研究生创新项目
赵庆龙(1989—),男,山东省人,硕士研究生,主要研究方向为光伏发电及新能源汽车。
