供应链环境下的多级库存优化及控制研究*

吴占坤，赵英姝

（齐齐哈尔大学经济与管理学院，黑龙江 齐齐哈尔 161006）

供应链环境下的多级库存优化及控制研究*

吴占坤，赵英姝

（齐齐哈尔大学经济与管理学院，黑龙江 齐齐哈尔 161006）

制造企业供应链的链接纽带是库存。在供应链管理环境下，企业既要使自身的利益最大化，还得促使整个供应链的利益的优化，而多级库存优化的目标就是追求整个供应链的利益最优化。因此，供应链的环境下的多级库存优化，在实际工作中具有非常重要的意义。文章建立了以制造商为核心、上游供应商和下游分销商组成的供应链库存系统，并在此基础上构建了多级库存的库存模型，最后用遗传学算法进行优化。

供应链；多级库存；成本优化；遗传学算法

1 供应链及库存控制相关理论

1.1 供应链的定义及类型

供应链是服务及消费品经过制造商、经销商、零售商最终到达消费者手中的过程。供应链是一个以核心企业为中心，由上游供应商、核心企业、下游分销商以及用户组成的网链结构[1]。供应链主要有以下特征：复杂性、动态性、交叉性、面向用户需求。

根据不同的标准，供应链通常有以下几种类型：①按照区分范围不同：分为内部供应链和外部供应链；②根据不同的稳定性：分为稳定的和动态的供应链；③针对不同尺寸的高度：分为平衡的供应链和倾斜供应链；④根据性能的不同：分为有效供应链和反应供应链[2]。

1.2 库存控制理论

（1）库存与库存成本。在企业的生产经营中，库存管理是其中的一个重要组成部分，实现了价值链估计值过程的重要部分在这个环节中。库存控制在供应链体系中是供应链管理的最大的阻碍，直接影响着节点企业的综合成本的是库存的持有量的高低，而且还会使整个供应链的整体绩效与性能受到牵制[3]。因此，想办法怎么样使库存成本最低，从而达到最好的效益，是每个企业管理者在实施供应链管理过程中必须要优先考虑的问题。建立一个针对市场变化相适应的库存也是一个企业建立供应链必须优先考虑的事情。

（2）库存控制策略与方法。供应链环境下的多级库存优化研究的最终目标是在整体的角度使各节点企业能够更好地进行生产经营活动[4]。从而降低库存，获得最大收益，并以尽可能低的库存成本获得尽可能高的客户满意度，在低成本与高收益、高客户满意度之间获得平衡，达到最优状态。库存控制策略主要有以下四种：①（R，Q）方法，持续查询固定订货量、固定订货点方法，属于定点补货方法，基础理论是企业对库存进行持续检查，当库存降到订货点水平R以下时，就发出一次订货，并且每次的订货批量都为固定值Q；②（R，S）方法，即持续查询最大库存量固定的方法，需要持续查询库存现状，也属于定点补货方法，当库存下降到库存订货点R以下时，发出一次订货，使库存量达到最大库存量S，即订货量为S-R；③（t，S）方法，定期查询最大库存量固定的方法，属于定期补货方法，不是持续查询库存，是每隔固定检查期t便检查一次库存，并且发出一次定货使库存量到达最大库存S，假如查询时现有库存水平为I，则订货量为S-I；④（t，R，S）方法，是定期查询固定订货点及最大库存量方法，该方法属于定期补货与定点补货相结合的方法，该方法设固定查询周期t，最大库存量S和固定订货点水平R，每隔一个检查周期 t 检查一次库存，若现有库存量I低于订货点水平R，则发出订货，使得库存量达到最大库存量S，即订货量为S-I，否则，不发出订货。

这里各个符号的含义：Q-指每次订货量；R-订货点水平；S-最大库存量；t-固定的检查周期。

2 供应链多级库存优化与控制

2.1 多级库存控制优化简介

多级库存优化与控制是基于单级库存控制建立的，基于多层次的阶段库存系统不同的配置，该系统具有串行、并行系统和总系统。多级库存优化是全球供应链库存管理优化模型。

（1）供应链库存成本的结构。库存成本的结构包括：①维持库存成本Ch；②交易成本Ct；③缺货损失成本Cs。

（2）供应链库存模型。在日常生活中可以看到供应链的无限层次，那么相对应的供应商、分销商都有无限的层级，最后到客户。下面从三级供应链的库存优化为基础进行研究。

Dit独立为每个节点的零售商的需求；Qit是根据变化需求的订货量，零售企业传递订货信息流到分销商，分销商给制造商传递订单信息，制造商进行生产，同时，上游企业为其提供一定的物料。这三个地方都会产生一定的库存，所谓的三级库存系统就产生了。假设每个零售商有自己的独立需求，客户的需求、订货提前期都是随机变量，并且销售一种产品，就产生了单一产品的供应链。多级供应链就是在他们之间的横向和纵向的交叉混合而成的，有如下模型：

其中：Cmfg是制造商库存成本，Ccd是销售商库存成本，Crd是零售商库存成本。

分析供应链的库存成本，有交易费用、存储费用和缺货损失。总的可以分为订货费与调拨费。库房k的订货费用有每次的交易费用（包括交易费用、购货费用、人工费用与运输费用）存储费用还有缺货损失费。

缺货损失：

存储费用：

因此，库房k的总订货费用为：

同样可以得到库房k的调拨总费用的构成跟其订货费一样但是应除去购货费，因为购货费是供应链的内部费用，按照上面讨论的，则不计入。具体计算如下：

缺货损失：

存储费用：

交易费用：

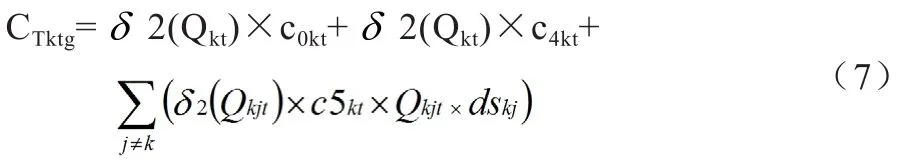
根据库存控制模型的目的，确定如下：

2.2 供应链环境下多级库存优化的实现

研究证明，遗传学算法在处理这方面的问题都好过其他的算法，下面就是具体介绍以遗传学优化模型具体的步骤，从而得到最优的解决方法。

（1）对仓库订货点与安全库存的确定。在以往和当前的实际情况的基础上，考虑库存满足率和交货时间，每个仓库的订货点和安全库存的确定SK、SSK，通常可以用以下公式来确定。

式中：μ为提前期内的需求的均值，p是客户满足率，Lk是平均订货周期。

（2）判断供应链库存状况。定期检查各仓库的实际库存，使：

（3）优化多级供应链订货。①初始种群的生成。依据上述可行域，随机生成一个个体，验证其是否满足，这样反复随机产生POPSIZE个个体，初始种群（POP1，POP2，…，POPPOPSIZE）就形成了；②选择复制。在上面已经获得了每个个体的适应度，并根据POPSIZE赌轮选择，重复POPSIZE个人等待交叉匹配操作；③交叉运算。一般选用的是交叉运算，父代可行那么子代就可行，若得不出最优解就需要进行变异运算；④变异操作。随机产生一个变异方向d=｛d1，d2，…dN｝，dk和Qk其中是的允许变化量。通过变异，就可以得出子代种群，经过检验不通过的则必须重新进行；⑤循环计算。反复操作（3）-（5）的程序，直到满足终止的前提，得到最优解POPo。

（4）对供应链环境下的多级库存调拨优化过程。这里选用的是矩阵形式的实数编码。所以对应的种群表示为以下所示。

式中的行是仓库，列是这个仓库的库存调动量，入为正，出则为负。根据约束条件可行域为：

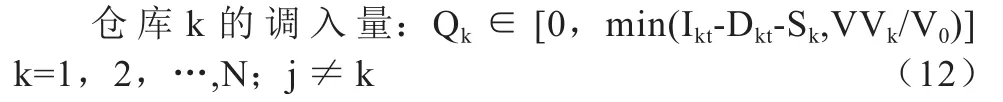
仓库k的调出量：

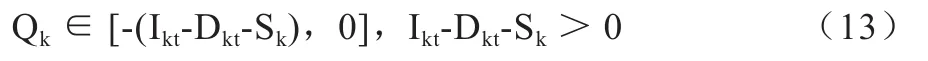
适应度：

2.3 结果与分析

在这里为了更好地研究多级库存优化调度，模拟一个多级库存进行计算。假设1P、2P、3P、4P、5P、6P、7P七个地方都有一个自己的库房，每个库房都存放同一样的产品纸箱。6P地的某个分销商需要该种型号的纸箱200个，而在6P地的仓库中，该种型号的纸箱只有80个，其他六地共有该种型号的纸箱400个。那么如何调配各仓库间的库存来满足6P地的需求，才能使总成本最小。假设仓库6P在这种情况下的需求率为40%，Lc为供应商到配送中心的运输时间，客户满足率p是90%。各个仓库的进货量不得大于仓库的最大仓库容量的105%，假设POPSIZE=10，Pc=0.5，Pm1=0.09，Pm2=0.06。

当不考虑缺货时间QC和缺货次数NC，而只考虑成本TC时，设置P1=160，P2=P3=0，可计得出一个最优解；若把POP0代入参数P1=160，P2=130，P3=100的公式中，就可以算出综合库存成本Z，就是POP0的情况下的真实的总库存成本；当把缺货时间QC与缺货次数NC列入考虑时，使P1=160，P2=130，P3=100，就可以得到另外的POPo*最优解，见表1。

表1中显示，假如把缺货次数与缺货时间放入考虑的话，算出的值估计会大一些，但是综合成本Z值是最小的，再加上考虑了m1，m2这两个安全因子，所以说POPo*的解可以更好的提高供应链下的多级库存优化。

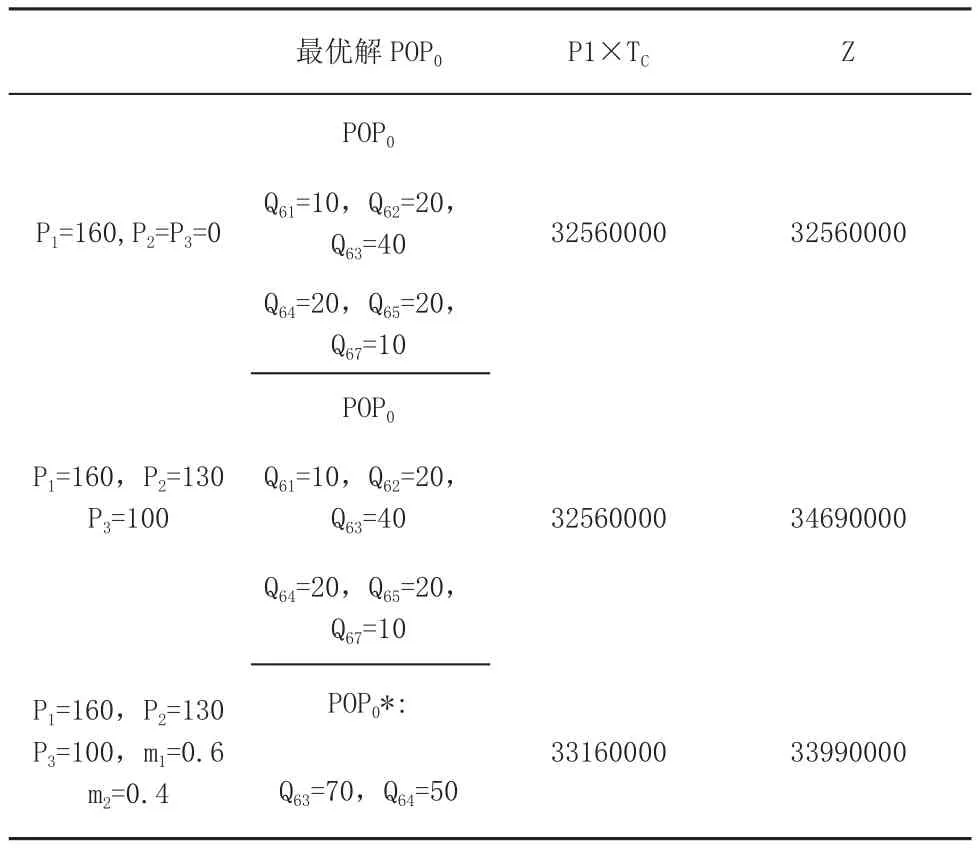
表1 两种模型结果比较

3 结束语

文章是供应链环境下的多级库存优化研究，同时也是供应链、系统多级库存、战略结构模型常用的库存分析方法。根据分销商和制造商建立最大限度地降低库存和减少库存模型的存货周转时间多目标的成本，建立多目标函数。在分析库存成本构成时，加入了运输成本。建立多目标模型时，考虑成本优化与时间优化作为研究的目标。供应链环境下的多级库存优化研究在实际工作中有非常重要的现实意义，因此很多学者都一直很努力的再这一领域内做研究。并且随着社会经济的发展，对供应链的要求越来越高，供应链的结构也在不断变化，这决定了多级库存控制策略与方法也在不断地提高与改善。

[1]马士华,林勇.供应链管理[M].北京:机械工业出版社,2011.

[2]叶怀珍.现代物流学[M].北京:高等教育出版社,2013.

[3]隋明刚,魏嶷综述:供应链库存成本研究的现状及其发展数据[J].物流技术,2010,(5).28-32.

[4] Ballou R.H.Business Logistics Management[M] .3rded.Prentice-Hall, Englewood Cliffs,NJ,2012.

[5]杨莹.我国供应链环境下多级库存优化研究综述[J].《新西部(理论版)》,2012,(7).146.

F27

A

2096-2789（2016）11-0225-02

齐齐哈尔大学青年教师科研启动支持计划项目（2011WM07）。

吴占坤（1977-），男，吉林松原人，硕士、副教授，研究方向：企业物流管理。