基于广义线性模型的岭型主成分估计及实例分析

王文军,杨幼玲

(东北林业大学)



基于广义线性模型的岭型主成分估计及实例分析

王文军,杨幼玲*

(东北林业大学)

在广义线性模型已有的参数估计的基础上，结合广义线性模型中的主成分估计和岭估计，给出了广义线性模型中的新的估计方法岭型主成分估计，并在均方误差意义下证明了在满足一定条件下这种估计方法是优于广义线性模型中的最大似然估计、主成分估计、岭估计的，最后通过实际算例对比分析验证了理论上得到的结果.

广义线性模型；岭型主成分估计

0 预备知识

广义线性模型作为一种常见的数学模型在数学领域有着非常广泛的应用，它对因变量的要求拓展到了指数族分布，常见的模型如Logistic模型、Poisson模型、负二项模型等都包含在内，因而对它的参数估计的研究具有非常重要的意义.经典线性模型中，Baye和Parker结合主成分估计和岭估计提出了岭型主成分估计，其中最小二乘估计、主成分估计和岭估计是它的一些特殊估计量.这种方法在经典线性模型中具有很多优良的性质，在广义线性模型中是否仍然适用，仍需要进一步地研究.

定义1[1]设因变量Y和自变量X1，X2，…，Xp的观测值，若

(1)Y1,Y2,…,Yn相互独立，且对每个i，Yi服从指数分布，即

c(y,φi))

(2)设ui为对应的Yi的数学期望值(i=1,2,…,n)，存在单调且可导函数g使得

则称Y与X1,X2,…,Xp服从广义线性模型(Generalized Linear Models，简称GLM).

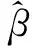
1 广义线性模型(GLM)的岭估计

GLM中岭估计的定义为：

其中k>0为偏参数值，X为已经中心化的设计矩阵，X′WX的特征值为λ1,…,λp，其中

λ1≥…≥λp，则正交矩阵 Φ=(φ1,…,φp)，φ1,…,φp为对应λ1,…,λp的标准化特征向量，Φ为p×p正交矩阵，则Φ′X′WXΦ=diag(λi)=Λ，设α=Φ′β，则β=Φα，则可进一步化简得:

2 广义线性模型(GLM)的主成分估计

当自变量存在复共线性时，X′WZ的特征值就会很小，近似于0，不妨设λr+1,…,rp≈0.λi度量了第i个主成分值的变动大小，当它的值接近于0时，它对回归自变量的影响将很小可忽略不计，故可将它从回归模型中剔除.

3 广义线性模型(GLM)的岭型主成分估计

GLM中的岭型主成分估计定义为：

其中k>0为可选参数(岭参数).

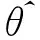
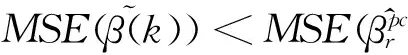
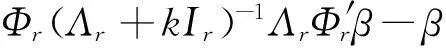
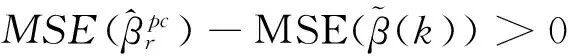
上式成立的充分条件左式的最小值大于右式的最大值即可，即

化简可得

上式成立的充分条件为左式的最小值大于右式的最大值即可，即

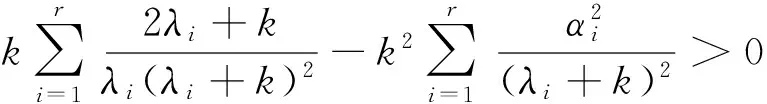
使上式成立的充分条件为：

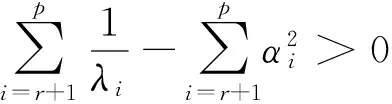
上式成立的充分条件为：

4 实例分析

对广义线性模型中非常典型的Poisson模型进行分析.数据全部采集于《中国统计年鉴—2006》[8]的环境保护篇，对2005年全国31个地区的大气污染物与污染次数相关的变量服从Poisson模型，文献[3]中已经用主成分估计进行了拟合，在此基础上进一步用岭估计、岭型主成分估计进行拟合数据.

对模型做岭回归，选取了101个λ值进行验证，如图1，广义交叉验证GCV最小时λ距离0值较近，进一步通过分析发现当岭参数k=0.6时参数误差基本稳定，通过对比岭参数k与MSE(均方误差)的关系如图2，验证了k=0.6时样本模型误差已经趋于稳定状态.

图1 与模型误差、广义交叉验证GCV关系图

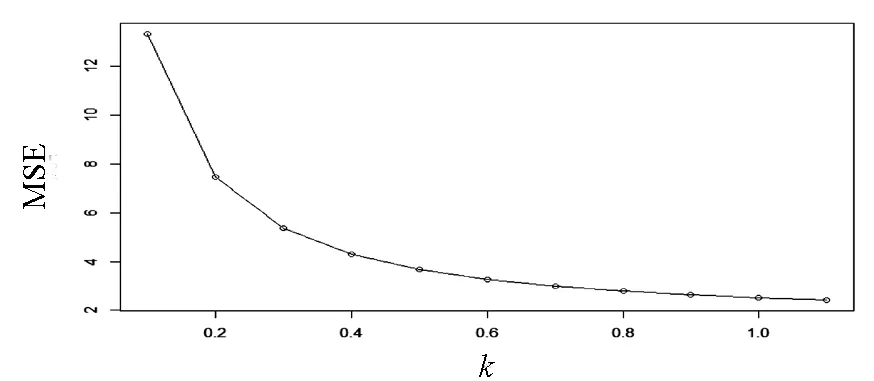
图2 模型均方误差与参数k的取值的关系

为了方便对比，岭型主成分估计选取的岭参数值与岭估计选取的岭参数值相同，选取的主成分个数也与主成分估计一样.

表1 几种方法拟合系数及均方误差对比表

表1中可看出，与最大似然估计比较，其他几种方法在系数变化上大体一致.对计算出的均方误差值进行比较可知，主成分估计、岭估计在很大程度上降低了误差值，而岭型主成分估计进一步降低了误差值，因而是优于它的组成估计的.

5 结束语

定理1、定理2、定理3分别证明了广义线性模型中的岭型主成分估计优于广义线性模型中的最大似然估计、主成分估计、岭估计所需要满足的条件.实际应用部分，利用Poisson模型进行分析，通过几种方法的模拟对比分析，很好地验证了理论上得到的结论，因而岭型主成分估计在广义线性模型中仍然大大降低了模型的均方误差，具有很好的优良性.

[1] 梅长林，王宁.近代回归分析方法[M].北京:科学出版社，2012.

[2] 王松桂，陈敏，陈立萍.线性统计模型：线性回归与方差分析[M].北京：高等教育出版社,1999.

[3] 杨幼玲.基于广义线性模型的主成分估计及实例分析[J]. 哈尔滨师范大学自然科学学报,2015, 31(5):33-36.

[4] Marx B D.Principal component estimation for generalized linear regression [J].Biometrika,1990,77(1):23-31.

[5] Segerstedt B. On ordinary ridge regression in generalized linear models [J]. Communications in Statistics-Theory and Methods, 1992,21(8):2227-2246.

[6] 黄介武,杨虎.线性与广义线性模型中参数估计的一些研究[D].2014.

[7] 李兵,陈国华.岭型主成分估计的优良性质[J].桂林电子科技大学学报,2009,29(2):128-130.

[8] 国家统计局.《中国统计年鉴-2006》[G]．北京：中国统计出版社,2006.

[9] 薛毅，陈立萍.统计建模与R软件[M].北京：清华大学出版社，2007.

[10] Baye M R, Parker D F .Combining ridge and principal component regression: A money demand illustration[J]. Communications in Statistics-Theory and Methods, 1984,13:197-205.

(责任编辑：于达)

Ridge Type Principal Component Estimation Based on Generalized Linear Models and its Analysis of the Practical Example

Wang Wenjun, Yang Youling

(Northeast Forestry University)

In this paper,on the basis of the existing parameter estimation of the generalized linear model, by combining principal component estimation and ridge estimation in generalized linear model , a new estimation method ridge type the principal component estimation of generalized linear model is presented. And in the sense of Mean Square Error (MSE) it proves that this estimation method is better than the maximum likelihood estimation, principal component estimation and ridge estimation in the generalized linear model under certain conditions . At last the theory of this paper is verified by practical example analysis results.

Generalized linear model; Ridge Type Principal Component Estimation

2015-04-23

O212

A

1000-5617(2016)03-0018-04

*通讯作者:651829820@qq.com