具有弱Allee效应的随机捕食-食饵模型全局正解的存在性 *

刘冠琦,汪洪艳

(1.哈尔滨师范大学;2.黑龙江八一农垦大学)



具有弱Allee效应的随机捕食-食饵模型全局正解的存在性*

刘冠琦1,汪洪艳2

(1.哈尔滨师范大学;2.黑龙江八一农垦大学)

在具有弱Allee 效应的Lotka-Volterra捕食-食饵模型基础上，加入随机白噪声干扰，讨论具有弱Allee效应的随机捕食-食饵模型全局正解的存在性.运用Itõ公式和李雅普诺夫函数，证明该模型的正解在有限时间内不爆破，存在全局正解.

弱Allee效应；随机；捕食-食饵模型；全局正解

0 引言

在生物数学中，捕食者和食饵的相互作用一直以来都是研究工作中的一个重要问题，由Lotka和Volterra[1]提出的捕食-食饵模型被广泛研究.同时，Allee[2]指出， Allee效应作为一个生物现象，刻画了种群规模或密度与其增长率之间的相关性.Allee效应广泛存在于许多自然种群中，包括植物、鸟、哺乳动物、昆虫等.种群密度必须具有一个最低的密度，以保证物种继续繁衍、育种，即Allee效应，如果种群密度低于这个最低的密度，种群将会灭绝.一个具有弱Allee 效应的Lotka-Volterra捕食-食饵模型，其模型可表示为[3]

(1)

其中，R和F分别表示时刻t食饵和捕食种群的数量，r表示食饵种群的内部增长率，A为种群Allee效应常量，a表示食饵种群环境容纳量，b表示捕食率与捕食种群与食饵种群相互的作用，c表示转化率和捕食种群和与食饵种群相互的作用，d表示捕食种群的死亡率，A，a,b,c,d均为正常数.另一方面，我们都知道，任何生态系统都不可避免地要受到环境噪声的干扰[4]，许多文献都引入随机模型来考虑生态系统的行为.该文考虑具有随机白噪声干扰的具有弱Allee效应的Lotka-Volterra捕食-食饵模型：

(2)

1 预备知识

设(Ω,F,P)为完备概率空间，滤子{Ft}t≥0为右连续的，F0包含所有的P-零空间.

定义

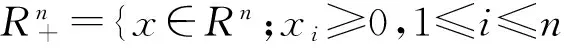
对d维随机微分方程，

dU(t)=f(U(t),t)dt+g(U(t),t)dW(t)

(3)

其初值U(t0)=U0∈Rn，W(t)表示(Ω,F,P)中d-维标准布朗运动.定义方程(4)相关联的微分算子为

(4)

那么当L作用在V∈C2,1(Rn×R+;R+)，得

dV(U(t),t)=LV(U(t),t)dt+VU(U(t),t)g(U(t),t)dW(t).

2 全局正解的存在性

证明 在t≥0，对给定初值x(0)=lnR0，

y(0)=lnF0，下面方程

的系数满足局部Lipschitz条件，所以存在着解

(x(t),y(t))定义在[0,τe]上[5]. 再由It公式，R(t)=ex(t),F(t)=ey(t)是模型(2)对应初值(R0,F0)的局部正解.

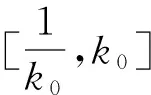
P(τ∞≤T)>ε，那么存在整数n1≥n0，使得

P(τk≤T)≥ε,∀n≥n1.

(6)

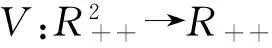
V=R-1-lnR+F-1-lnF.

(c-b)RF+K≤C,

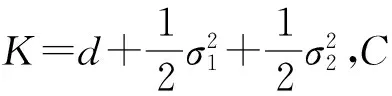
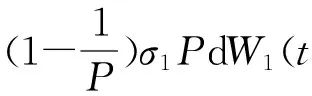
EV(R(τk∧T),F(τk∧T))≤V(R0,F0)+CT

(7)

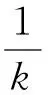
再由(7)式，

V(R0,F0)+CT≥E[1Ωk(ω)V(R(τk),

令n→∞，得到

∞>V(R0,F0)+CT=∞.

[1] 陈兰荪，宋新宇，陆征一. 数学生态学模型与研究方法[M]. 成都：四川科学技术出版社，2003.1-15.

[2] Allee W C, Animal Aggregations. A study in General Sociology. University of Chicago Press. Chicago,1931.431.

[3] Bai Z J, Wang W S, Li X P. Qualitative Analysis of a Predator-prey system with Allee effect for prey[J]. Annals of Differential Equations, 2007, 4(4):386-390.

[4] Gard T C. Stability for multispecies population models in random environments[J]. Nonlinear Anal, 1986, 10:1411-1419.

[5] Mao X R. Stochastic Differential Equations and Their Applications. Chichester Horwood Publishing, 1997.

(责任编辑：于达)

The Existence of the Global Positive Solution for a Stochastic Prey-predator Model with Weak Allee Effect

Liu Guanqi1, Wang Hongyan2

(1.Harbin Normal University;2.Heilongjiang Bayi Agricultural University)

In this paper, the stochastic white noise to a Lotka-Volteera prey-predator model with weak Allee effect is considered, the existence of the global positive solution for a stochastic prey-predator model with weak Allee effect is discussed. By using Itformula and Lyapunov function, the positive solution will not explode in limited time is proved, there exists a positive solution.

Weak Allee effect; Stochastic; Prey-predator model; Global solution

2016-02-26

*黑龙江省教育厅科学技术研究项目(12531202)

O21

A

1000-5617(2016)03-0004-02