关于线性代数教学设计的几点反思与探讨

2016-12-15胡超竹

西部皮革 2016年20期

关键词：例题向量知识点

胡超竹

(湖北工业大学理学院，湖北武汉 430068)

关于线性代数教学设计的几点反思与探讨

胡超竹

(湖北工业大学理学院，湖北武汉 430068)

本文首先介绍了在教学过程中，学生学习线性代数这门课程的过程中普遍存在的三种不良现象，一是从课程开始就抱有惧怕与怀疑态度，二是零散且无法准确地记忆知识点容易产生混淆，三是忽视例题重要性与排斥解题思路的多样性。然后针对这些现象进行反思分析原因，最后在教学设计的层面上去探讨相应的解决方案，特别是如何引导学生建立合理有效的知识体系。

线性代数；教学设计；现象；知识体系

线性代数作为大学高等教育中的一门基础学科，它的重要性和广泛应用是不言而喻的。而且在不同大学不同专业的大学生培养计划中，线性代数作为一门公共必修课有着共同的特点：学时紧张，课程知识点多，抽象性综合性强。大多数大学生对线性代数的感官是比高等数学要难，然而对于教师而言，却认为线性代数比高等数学要简单，造成这个现象的原因是多方面的。我认为最为根本的原因是数学教师早已在多年的学习和教学中，习惯了用数学思维去思考分析问题，用数学方法去解决问题。大学生作为初学者，他们如果没有很好的引导，是无法在较短的时间内最高效地学习该课程的基本理论知识，熟练掌握方法灵活地解决问题。

教师想要好的教学效果，就必须要有好的教学设计。教学设计涵盖了课前备课、课堂教学中的黑板板书、电子课件、言语表达与作业布置，课后与学生的交流辅导方式等多方面。在本文中仅针对线性代数这门课程，根据学生在学习过程中所反应出的三种谱遍存在的不良现象，去反思原因，且在教学设计层面上去探讨相应的解决方案，引导帮助学生去改善这些不良的现象。

其一，学生对于线性代数教材的最初感官是只有数学符号和文字，相较于高等数学教材里一些具体的图像表格，似乎更加抽象。从而他们会有一种潜意识的怀疑和惧怕，怀疑这门课并不实用，惧怕学习高度抽象化的理论知识。学生如果从一开始就以这样的感官去对待这门课程，这种消极的态度会极大的影响学习效果，更甚至一开始就放弃此门课程的学习。

那么，作为教师，需要重视整个教学进程中第一节课的教学设计。首次课是一个起点，教师在这个起点里，首先，必须引导学生正确认识此课程的重要地位，激发学生学习此课程的兴趣。特别是工科与理学的学生，需要告知他们线性代数中的知识会作为有效的工具在他们各自的专业领域里广泛应用，在后期也可以与相关软件如matlab相结合去解决生活中更多的实际问题。其次，帮助学生建立可以学好此课程的信心。线性代数这门课程本质上是利用新的工具如行列式、矩阵和初等变换等进行代数运算，求解线性方程组。并没有对学生的中学数学基础有高的要求，所有的学生在同一起跑线，只要拥有良好的学习态度、正确的学习方法都可以得到好的学习效果。教师也需要告诉学生，在以后课程中，作为老师一定会随时与他们交流，陪伴着他们，给予学生信任感。这些方面是教师可以更好地完成课程教学的奠基石。另外，需要引导学生阅读教材目录，帮助学生从全局上去掌握线性代数的整个知识体系，从而更准确地认识学习这门课程的目的，具体可如下：

上图中第一个方框里的四个内容是预备知识，是基础和工具，中间则是主体和重点，最后两个内容是更为综合性的应用体现。

其二，学生对于线性代数中极多的定义定理和推论感到畏惧和厌烦，无法记忆全部，也无法记忆准确，极易混淆。造成这种现象的原因主要是，学生在学习过程中零散地去看待每一个知识点，并没有重视知识点之间的联系，也没有将相关的知识点放在一起作比较，形成完整的知识体系，总而言之学习方法不科学。

因此，作为教师在每一次的课堂教学中，学习新章节内容前，引导学生快速翻阅教材相应章节寻找出关键词，自己发掘重点内容。教师在其后的讲授过程中同样以这些关键词作为主线节点，教材中具体的定义、定理、推论作为分支，系统地去介绍此版块内容，帮助学生建立每个版块内容的知识体系。这种方法也需要教师在课程教学中以黑板板书或者电子课件的形式直白地展现给学生，给学生作为样本。例如

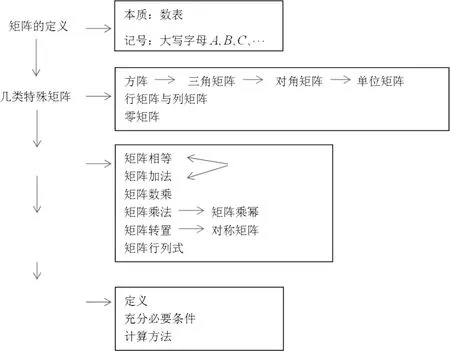
以上是对于矩阵这个版块内容的部分知识点梳理，利用关键词作为主线节点，用图形符号如箭头符号将所有知识点串联起来，形成体系，并且在在教学过程中以这个体系为主体框架，用具体的定理和推论为外围分支补充这个体系。教师可以要求学生以这种知识体系为模板，梳理每一章的知识点作为作业任务，引导学生形成良好的学习习惯。这种引导可以使得学生不再惧怕记忆知识点，也可以帮助学生更系统地去理解知识。

另外针对学生对于知识点的记忆混淆，同样，教师可以引导学生将不同板块却类似或联系紧密的知识点整合起来。例如学生学习向量组、向量空间、齐次线性方程组解向量空间与极大无关组、基、基础解系，秩和维数等这些定义很容易混淆，对于之间的关系比较困惑。那么，在授课中可尝试给出这样的知识框架：

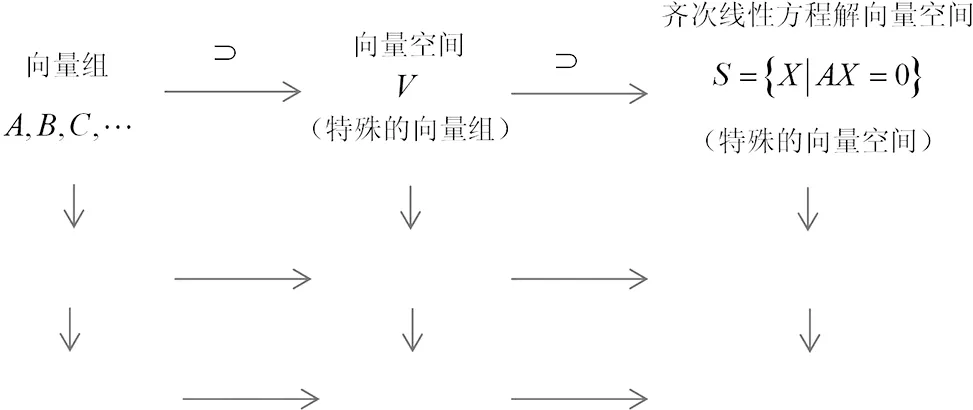
针对以上的框架可以具体解释为向量组是包含向量空间的，向量空间又包含齐次线性方程组解向量空间，向量组有自身的极大无关组和秩，那么向量空间的极大无关组称为基，齐次线性方程组解向量空间的基称为基础解系，向量空间的秩成为维数，齐次线性方程解向量空间的秩也成为维数。总的来说，极大无关组、基与基础解系本质是同样的定义，只是针对不同对象名称不同而已，维数与秩也是如此。这样的框架可以帮助学生更加清晰的理解这些定义的本身，又不容易混淆。

其三，学生不重视教师在课堂上所讲授的例题，忽视老师针对同一类题型中所介绍的多种思维方式与解题方法。

线性代数教材是有这大量的例题，每一个例题是对相应的知识点最直接的应用，例题同样帮助学生了解为什么要学习这个知识点。所以在课堂教学中，教师需要时刻提醒学生重视例题，引导学生自己去总结各个章节中最具代表性的重要例题，并集中做好归纳笔记。