分数槽永磁同步电动机优化分析

黄光建，吴帮超，方超，朱兴旺

(广东工业大学自动化学院，广东广州510006)



分数槽永磁同步电动机优化分析

黄光建，吴帮超，方超，朱兴旺

(广东工业大学自动化学院，广东广州510006)

简要分析了分数槽永磁同步电动机电枢磁场的谐波，利用Maxwell 2D有限元分析软件分别仿真计算了36槽30极、32极、34极三台永磁同步电动机的永磁体磁场，通过傅里叶分解得到永磁体磁场的各次谐波及幅值，进行了径向力波分析。通过径向力波分析结果确定最佳的槽极配合，同时分析了不同极弧系数对永磁同步电动机齿槽转矩的影响。此分析方法对永磁同步电动机的优化设计具有一定的参考价值。

永磁同步电动机；分数槽；径向力波；极弧系数；齿槽转矩

0 引言

随着永磁材料性能的不断提高，尤其是具有高剩磁、高矫顽力的特点，永磁电机以其体积小、结构紧凑简单、重量轻、运行可靠、效率高以及电机的尺寸和形状灵活多样等优点，越来越广泛地应用于高性能的速度和位置控制系统[1]。

根据每极每相槽数q是否为整数可分为整数槽电机和分数槽电机。永磁电动机的电枢绕组采用分数槽方案已成为重要的发展方向之一，国内外许多公司已在永磁电动机系列产品上采用分数槽绕组方案。它具备以下优点：槽满率高；能够改善反电动势波形的正弦性；分数槽集中绕组缩短了线圈周长和绕组端部伸出长度，降低用铜量，绕组电阻减小，铜损耗随之减少，能够提高电动机的效率和降低温升[2]。但是永磁电机的电磁振动噪声与齿槽转矩是永磁电机优化设计必须考虑和解决的问题。文献[3]是基于不同槽配合、不同绕组配置的永磁电动机,提出了一种径向电磁力谐波的模数和频率解析表达式。文献[4]推导了磁极偏移时齿槽转矩的表达式并根据不同偏移角度来削弱永磁电机的齿槽转矩。

本文从理论上分析了分数槽永磁同步电动机电枢磁场的谐波次数，利用Maxwell 2D有限元分析软件对分数槽永磁同步电动机进行建模，分别计算了36槽30极、32极、34极三台永磁同步电动机的永磁体磁场，通过傅里叶分解得到磁场的各次谐波及幅值，进行径向力波分析。通过径向力波分析结果来确定36槽30极槽极配合，同时分析了不同极弧系数对齿槽转矩的削弱情况，存在一个最佳的极弧系数使得永磁同步电动机的齿槽转矩的幅值最小。

1 分数槽永磁同步电动机电枢磁场谐波分析

分数槽永磁同步电动机是指每极每相槽数q=Z/2pm=N/D=分数的电动机，其中D≠1，且N和D是没有公约数的。对于三相60°相带分数槽绕组电动机，当D为偶数时，单元电机数t=2p/D，定子绕组谐波磁场的谐波次数为：V=±2(3k±1)/D；当D为奇数时，单元电机数为t=p/D，定子绕组谐波磁场的谐波次数为：v=±(6k±1)/D，式中k=0,1,2,3…；两个“±”号应取得一致，带负号谐波的旋转方向与不带负号的相反。

(1)定子槽数Z=36，电机极数2p=30

定子绕组谐波磁场极对数为

V=±p(6k±1)/D，式中k=0,1,2…

即3、-15、21、-33、39、-51、57…

(2)定子槽数Z=36，电机极数2p=32

定子绕组谐波磁场的极对数为

V=±2p(3k±1)/D，式中k=0,1,2…

即4、-8、16、-20、28、-32、40、-44、52…

(3)定子槽数Z=36，电机极数2p=34

定子绕组谐波磁场极对数为

V=±p(6k±1)/D，式中k=0,1,2…

即1、-5、7、-11、13、-17、19、-23、25…

2 分数槽永磁同步电动机永磁体磁场分析

在Maxwell 2D模型中，将电枢绕组电流设置为零，可以得到永磁体磁场如图1所示。再通过傅里叶分解可得到各磁场谐波极对数以及各谐波幅值如表1所示。

表1可以看出，在永磁同步电动机的永磁体谐波磁场中，3次谐波磁场(36槽/30极、36槽/32极和36槽/34极电动机对应的3次谐波磁场分别为45对极、48对极和51对极)幅值较大。此外，36槽/34极永磁同步电动机永磁体磁场的119对极(7次谐波)谐波磁场的幅值也比较大。

3 不同槽极配合永磁同步电动机的径向力波分析

根据力学理论可得，力波引起定子铁心的振动幅值Av与振动频率，径向电磁力和力波次数的关系可近似为

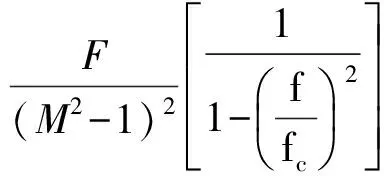
(1)

式中，力波次数M≠1,M=ν±μ，ν—电枢磁场谐波极对数；μ—永磁体磁场谐波极对数；fc—定子铁心的固有频率；f—振动频率；F—径向电磁力[5]。

从式(1)中可以得到，振动幅值与(M2-1)2成反比关系，如果M值较大则振动幅值与M4成反比。由此可见，力波次数对振动幅值影响极大，会引起电动机较大的电磁噪声。同样大小的电磁力，如果力波次数值变大则振动幅值会显著减小，电动机的电磁噪声则会进一步降低。表2、表3、表4分别是36槽30极、32极、34极永磁同步电动机径向力波次数表。

表2 36槽30极径向力波次数表

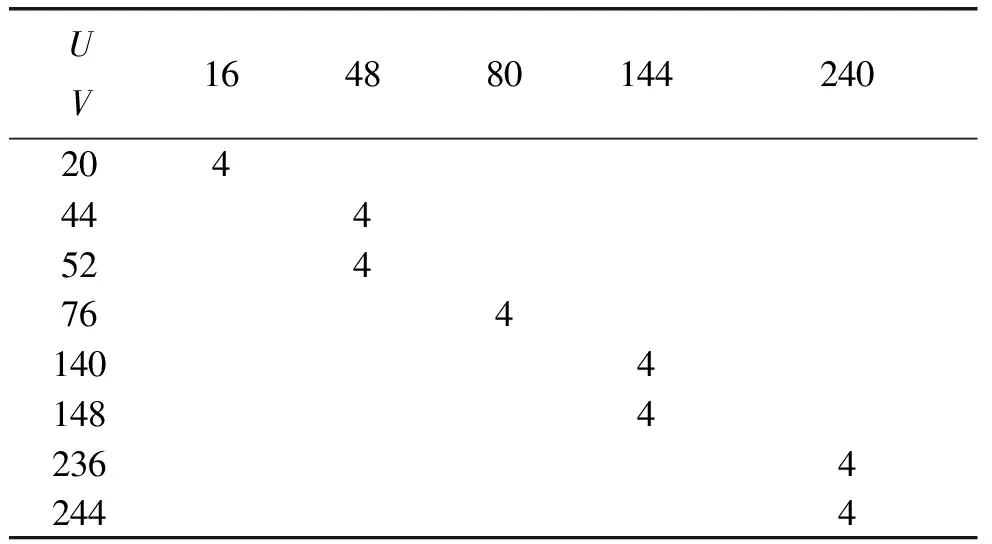
表3 36槽32极径向力波次数表

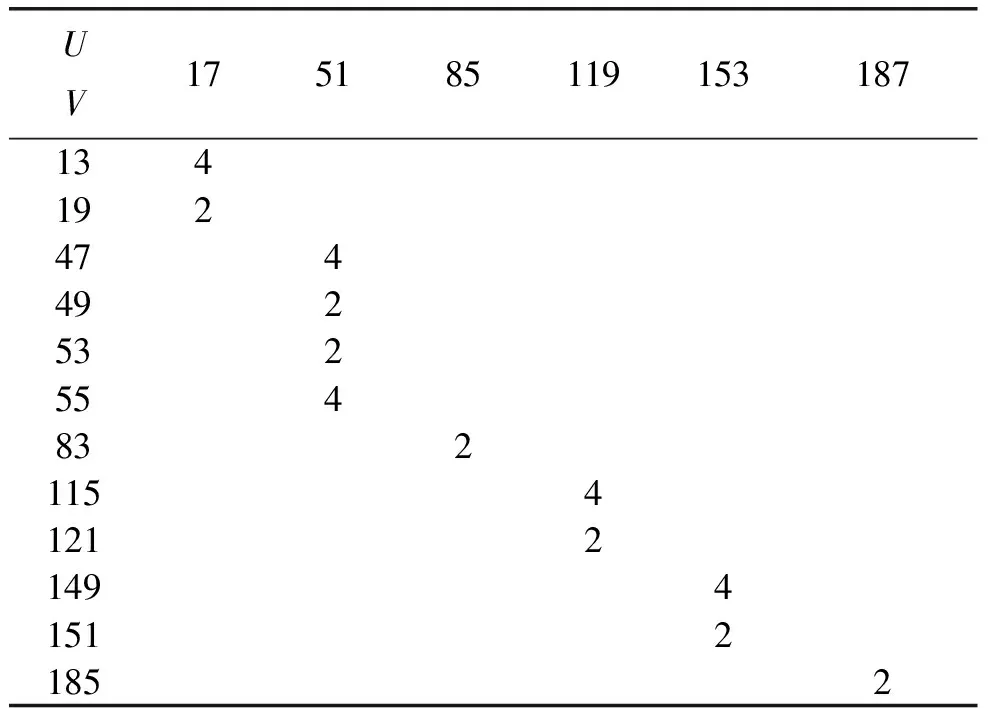
表4 36槽34极径向力波次数表

在分析电动机振动与噪声时，由式(1)中可见4阶以上力波次数对振动幅值的影响不大，可以不予考虑的。对照表2、表3、表4的结果，可以看出：36槽/30极电动机只产生0阶径向力波，0阶力波不会使定子铁心产生不对称的弯曲变形，有利于降低电动机的振动与噪声；36槽/32极电动机除产生0阶径向力波外，还产生4次阶径向力波； 36槽/34极电动机则产生除0阶径向力波和4阶径向力波外，还产生大量2阶径向力波。实验研究表明，2阶径向力波是对电磁噪声影响最大。故本文采用36槽30极槽极配合。

4 齿槽转矩的解析分析

在永磁电机中，由于齿槽的存在，不可避免地会产生齿槽转矩。齿槽转矩是永磁电机的特有问题，它的存在会导致转矩波动，引起电机的振动与噪声，影响系统的控制精度[6]。齿槽转矩可定义永磁电机不通电时磁场能量对定转子相对位置角的负导数

(2)

假设电枢铁心的磁导率为无穷大，永磁体磁导率与空气相同，电机的磁场能量可近似表示为电机气隙和永磁体中存储的磁场能量之和，即

(3)

气隙磁密可表示为

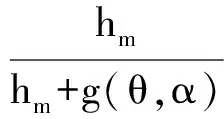
(4)

式中，Br—永磁体剩磁磁密；hm—永磁体充磁方向长度沿圆周方向的分布；g—气隙长度。

将Br2(θ)和G2(θ,α)进行傅里叶展开可得

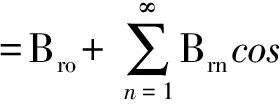
(5)

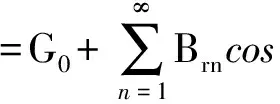
(6)

故不考虑斜槽时齿槽转矩表达式可表示为

(7)

式中，z—槽数；2P—极数；La—电枢铁心的轴向长度；对本文外转子永磁同步电动机来说，R1、R2—定子外半径和转子轭内半径；n—nz/2p为整数的整数。

4.1 基于极弧系数削弱齿槽转矩

削弱齿槽转矩的方法主要有三类：改变磁极参数；改变电枢参数；电枢槽数与极数的合理配合。本文采用极弧系数的方法去削弱齿槽转矩，是属于改变磁极参数。极弧系数是指磁极极弧宽度和磁极极距之比，由式(7)可得对齿槽转矩幅值影响极大，但并不是所有的傅里叶分解系数都能对齿槽转矩产生影响，只有nz/2p次谐波对齿槽转矩产生作用，因此必须想办法削弱nz/2p次谐波的幅值。通过改变永磁电机的极弧系数可以削弱nz/2p次谐波幅值。图2是不同极弧系数时齿槽转矩的波形。极弧系数所对应的齿槽转矩幅值如表5所示。

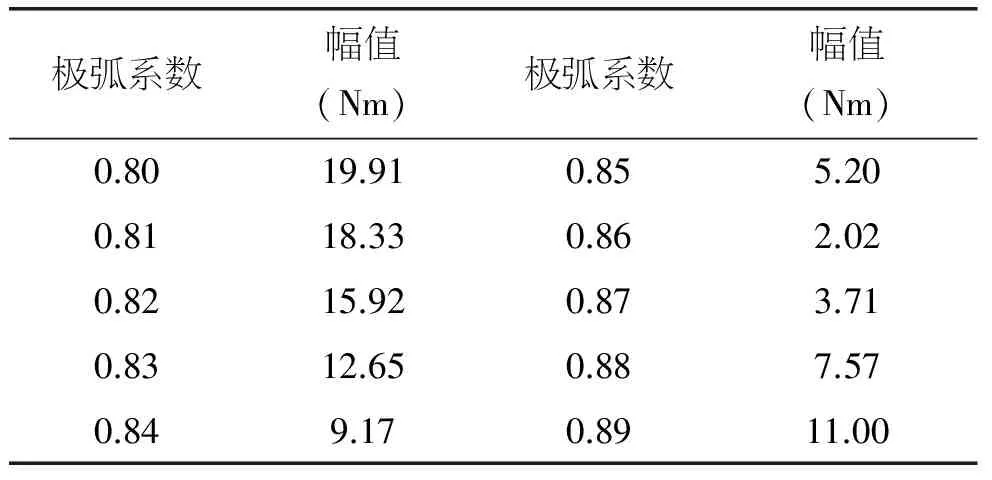
图2 不同极弧系数时齿槽转矩的波形

从图2，表5可以明显看出当极弧系数为0.86时，齿槽转矩幅值最小。齿槽转矩幅值的降低有利于抑制永磁电动机的振动与噪声。

5 输出转矩

永磁同步电动机在稳定运行时的输出转矩波形见图3。

图3 电动机的输出转矩

由图3可知，永磁体优化后输出转矩波形比优化前输出转矩波形更加平滑。优化前输出转矩的平均值为652.66 N·m，优化后输出转矩的平均值为663.68 N·m，最大值为679 N·m，最小值为647.33 N·m。转矩波动率γ可以反映电动机输出转矩的平稳性[3]，表达式为式(8)所示，代入相关数据可得γ=4.8%，表明了此永磁同步电动机转矩波动小，电动机的性能良好。

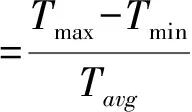
(8)

式中，Tmax—最大转矩；Tmin—最小转矩；Tavg—平均转矩。

6 结语

本文从理论上分析了分数槽永磁同步电动机电枢磁场的谐波次数，利用Maxwell2D有限元分析软件分别仿真计算了36槽30极、32极、34极三台永磁同步电动机的永磁体磁场，通过傅里叶分解得到永磁体磁场的各次谐波及幅值，进行了径向力波分析。径向力波分析结果表明36槽30极永磁同步电动机更有利于降低电动机的振动与噪声。同时分析了不同极弧系数对齿槽转矩的削弱情况，永磁体优化后电动机的输出转矩的波形更加平滑，平均值更大。本文的分析方法对永磁同步电动机的优化以及电磁振动噪声的研究具有一定的参考价值。

[1] 唐任远.现代永磁电机[M].北京:机械工业出版社,1997.

[2] 谭建成.永磁无刷直流电机技术[M].北京:机械工业出版社,2011.

[3] 杨浩东.永磁同步电机电磁振动分析[D].浙江:浙江大学,2011.

[4] 杨玉波,王秀和,张鑫,等.磁极偏移削弱永磁电机齿槽转矩方法[J].电工技术学报,2006,21(10):22-25.

[5] 许实章.交流电机的绕组理论[M].北京:机械工业出版社,1985.

[6] 王秀和.永磁电机[M].北京:中国电力出版社,2007.73-75.

[7] 陈贤阳,黄开胜,等.五相永磁容错电机设计与故障控制[J].电机与控制应用，2014,41(8):22-27.

Optimal Analysis on Fractional-Slot Permanent Magnet Synchronous Motors

HuangGuangjian,WuBangchao,FangChao,andZhuXingwang

(College of Automation Engineering, Guangdong University of Technology, Guangzhou 510006, China)

Harmonic of armature magnetic field of fractional-slot permanent magnet synchronous motor (PMSM) was briefly analyzed. Simulation calculations for magnetic fields of permanent magnets of three PMSMs with 36 slots and 30,32,34 poles were respectively carried out by finite-element software of Maxwell 2D. Various order harmonics and amplitudes of magnetic fields of permanent magnets were obtained by Fourier decomposition, and radial force waves were analyzed. The optimal slot/pole combination was confirmed based on analysis result of radial force wave, and the influence of pole-arc coefficient on cogging torque of PMSM was analyzed simultaneously. The analysis method in this paper has a certain reference value in optimal design of PMSM.

PMSM；fractional slot；radial force wave；pole-arc coefficient；cogging torque

10.3969/J.ISSN.1008-7281.2016.06.08

TM351

A

1008-7281(2016)06-0024-005

黄光建 男 1990年生；在读硕士研究生,研究方向为外转子永磁同步电动机的设计.

2016-04-29