Strong convergence theorems for a countablefamily of pseudocontractions in Hilbert spaces

KONG Zhaorong

(Economics Management Department,Shanghai University of Political Science and Law,Shanghai 201701,China)



Strong convergence theorems for a countablefamily of pseudocontractions in Hilbert spaces

KONG Zhaorong

(Economics Management Department,Shanghai University of Political Science and Law,Shanghai 201701,China)

This paper is devoted to the convergence analysis of a three-step hybrid viscosity approximation method for finding a common fixed point of a countable family {Tn}n≥1of uniformly Lipschitz pseudocontractions in a real Hilbert space.Without uniformly closed condition of {Tn}n≥1,we establish some strong convergence theorems for this method.The results presented in this paper improve and extend the corresponding results in the earlier and recent literature.

pseudocontraction; uniformly lipschitz; strong convergence; fixed point; viscosity approximation method

1 Introduction

(1)

Note that (1) can be equivalently rewritten as

It is well known that there exists a close connection between pseudocontractions and the important class of nonlinear monotone mappings,where a mappingAwith domainD(A) and rangeR(A) inHis called monotone if

〈Ax-Ay,x-y〉≤0, ∀x,y∈D(A).

It is clear thatAis monotone if and only ifT:=I-Ais pseudocontractive,and thus a zero ofA,x∈N(A):={x∈D(A):Ax=0},is a fixed point ofT,x∈F(T):={x∈D(T):Tx=x}.It is now well known (see [2]) that ifAis monotone then the solutions of the equationAx=0 correspond to the equilibrium points of some evolution systems.Consequently,considerable research efforts,especially within the past 20 years or so,have been devoted to iterative methods for approximating fixed points ofTwhenTis pseudocontractive (see [3-6] and references therein).In 1974,Ishikawa[1]introduced an iteration process,which in some sense is more general than that of Mann[7]and which converges to a fixed point of a Lipschitz pseudocontractive self-mappingTonC.The following theorem was derived.

Theorem 1.1[1]IfCis a compact convex subset of a Hilbert spaceH,T:C→Cis a Lipschitz pseudocontractive mapping andx0is any point ofC,then the sequence {xn} converges strongly to a fixed point ofT,where {xn} is defined iteratively for each integern≥0 by

(2)

where {αn},{βn} are sequences of positive numbers satisfying the conditions:

The iteration method(2)in Theorem1.1,which is now referred to as the Ishikawa iterative method,has been studied extensively by many authors.However it remains an open question whether or not this method can be employed to approximate fixed points of Lipschitz pseudocontractive mappings without the compactness assumption onCorT;see[5,8-9].

Very recently,Li,et al.[10] introduced and analyzed a three-step hybrid viscosity approximation method for finding a common fixed point of a countable family of uniformly closed and uniformly Lipschitz pseudocontractive mappings.The following theorem was proved.

(3)

wheref:C→Cis a contractive mapping with contractive constantδ∈(0,1) and {αn},{βn},and {γn} are sequences in (0,1) satisfying the following conditions:

Then{xn}converges strongly tox*∈F.

It is remarkable that there is the uniformly closed condition imposed on the countable family{Tn}n≥1 of uniformly Lipschitz pseudocontractive mappings.Naturally,we wonder whether the uniformly closed condition in Theorem1.2can be replaced by the other one.By virtue of Plubtieng and Ungehittrakool[11],we give an affirmative answer to this problem.

In this paper,we continue the study of the three-step hybrid viscosity approximation method(3)for finding a common fixed point of a countable family{Tn}n≥1 of uniformly Lipschitz pseudocontractions onC.We derive some strong convergence results for this method under the requirement that the uniformly closed condition in Theorem1.2is replaced by the following one:

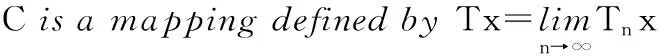
Compared with the above Theorems 1.1 and 1.2,our results drop both the compactness assumption onCin Theorem 1.1 and the uniformly closed condition on {Tn}n≥1in Theorem 1.2.

2 Preliminaries

In the sequel,we also need the following definition and lemmas.

LetHbe a real Hilbert space.Define the functionφ:H×H→Ras follows:

It is clear from the definition of the functionφthat

The functionφalso has the following property:

φ(y,x)=φ(y,z)+φ(z,x)+2〈z-y,x-z〉, ∀x,y∈H.

(4)

Lemma 2.1[12]The following holds:

The following lemma is a direct consequence of the inner product.Thus,its proof is omitted.

Lemma 2.2 The following holds:

3 Main results

LetCbe a nonempty,closed,and convex subset of a real Hilbert spaceH.Let {Tn}n≥1:C→Cbe a countable family of uniformly Lipschitz pseudocontractive mappings.Throughout this section,we assume that the following conditions (a) and (b) hold:

In this section, we consider and analyze the three-step hybrid viscosity approximation method (3) for finding a common fixed point of the countable family {Tn}n≥1of uniformly Lipschitz pseudocontractive mappings. We are now in a position to prove our main results. In the following theorem,the uniformly closed condition is replaced by the above conditions (a) and (b).

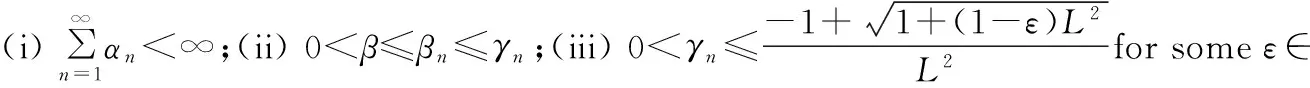
Proof Letp∈F.Then from (3) and Lemma 2.2,we have

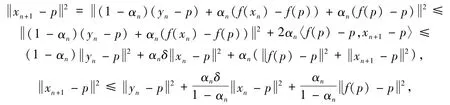
(5)

(6)

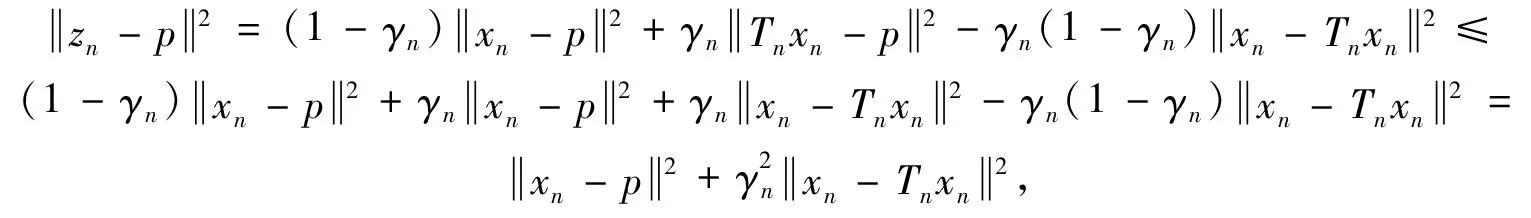
(7)

and

(8)

Substituting (7) and (8) into (6) we have

(9)

(10)

Thus,from (3) we have

(11)

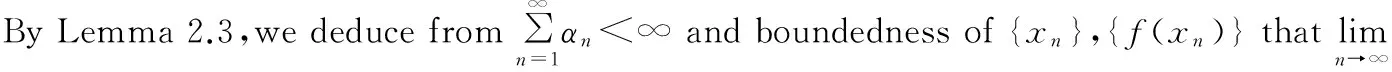
On the other hand,from(4)we have

(12)

(13)

Then from(12)and(13)we obtain

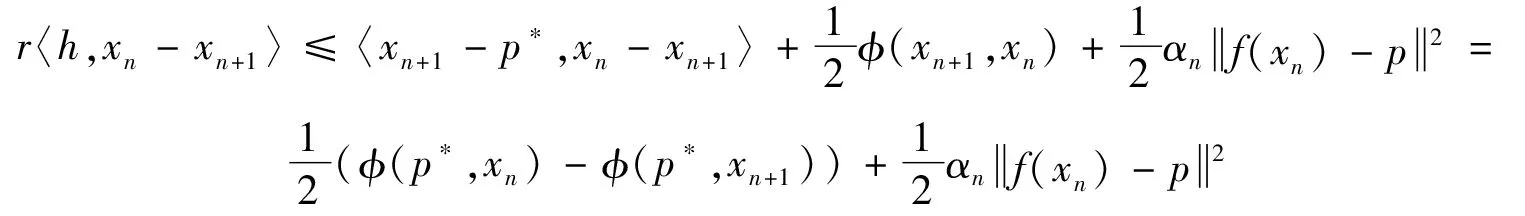
and hence

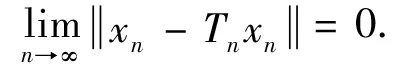
PutD={xn:n≥1}.Then it is clear thatDis a bounded subset ofC.Thus,by condition (a),there exists an increasing,continuous and convex functionhDfrom [0,∞) into [0,∞) such thathD(0)=0 and

In terms of Lemma 2.4,we get

(14)

Taking into account

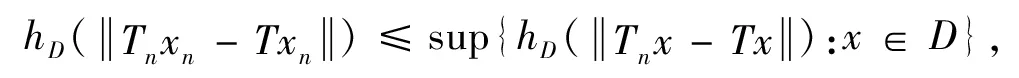
and according to (14),we have

Hence the properties ofhDyields

Noticing that

we get

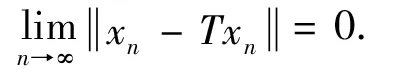
(15)

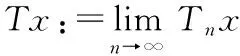
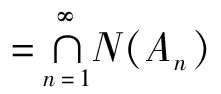
(16)

wheref:H→His a contractive mapping with contractive constantδ∈(0,1),and {αn},{βn} and {γn} are sequences in (0,1) satisfying the following conditions:

[1] Ishikawa S.Fixed points by a new iteration method [J].Proc Amer Math Soc,1974,44:147-150.

[2] Zeidler E.Nonlinear functional analysis and its applications,part II:Monotone Operators[M].Berlin:Springer,1985.

[3] Chidume C E,Mutangadura S A.An example of the Mann iteration method for Lipschitz pseudocontractions [J].Proc Amer Math Soc,2001,129:2359-2363.

[4] Chidume C E,Moore C.The solution by iteration of nonlinear equations in uniformly smooth Banach spaces [J].J Math Anal Appl,1997,215:132-146.

[5] Zegeye H,Shahzad N,Alghamdi M A.Convergence of Ishikawa′s iteration method for pseudocontractive mappings [J].Nonlinear Anal,2011,74:7304-7311.

[6] Cheng Q Q,Su Y F,Zhang J L.Convergence theorems of a three-step iteration method for a countable family of pseudocontractive mappings [J].Fixed Point Theory Appl,2013(1):1-14.

[7] Mann W R.Mean value methods in iteration [J].Proc Amer Math Soc,1953,5:506-510.

[8] Chidume C E,Moore C.Fixed point iteration for pseudocontractive maps [J].Proc Amer Math Soc,1999,127:1163-1170.

[9] Zhou H.Convergence theorems of fixed points for Lipschitz pseudo-contractions in Hilbert spaces [J].J Math Anal Appl,2008,343:546-556.

[10] Li S X,Ceng L C,Hu H Y,et al.Strong convergence of three-step iteration methods for a countable family of generalized strict pseudocontractions in Hilbert spaces [J].Fixed Point Theory Appl,2014(1):1-18.

[11] Plubtieng S,Ungchittrakool K.Approximation of common fixed points for a countable family of relatively nonexpansive mappings in a Banach space and applications [J].Nonlinear Anal,2010,72:2896-2908.

[12] Takahashi W.Introduction to Nonlinear and Convex Analysis [M].Yokohama:Yokohama Publishers,2009.

[13] Tan K K,Xu H K.Approximating fixed points of nonexpansive mappings by the Ishikawa iteration process [J].J Math Anal Appl,1993,178:301-308.

(责任编辑:冯珍珍)

Hilbert空间中可列个伪压缩映像的强收敛定理

孔兆蓉

(上海政法学院 经济管理学院,上海 201701)

研究实 Hilbert空间中寻求可列个一致Lipschitz伪压缩映像之公共不动点的三步混合粘性逼近法的收敛性.在缺乏它们的一致闭条件下,建立了该方法的强收敛定理.所得定理改进与推广了文献中早期与最近的有关结果.

伪压缩映像; 一致Lipschitz映像; 强收敛; 不动点; 粘性逼近法

Foundation item: This research was supported by the Project for Development Program of Young Teachers in Higher Education Institutions,Shanghai (ZZszf15015).

KONG Zhaorong,Economics Management Department,Shanghai University of Political Science and Law,Shanghai 201701,China.E-mail:kongzhaorong@163.com

O 177.91 Document code: A Article ID: 1000-5137(2016)05-0511-07

10.3969/J.ISSN.1000-5137.2016.05.001

Received date: 2016-09-12