非均匀杂波背景下双基地MIMO雷达距离扩展目标的GLRT检测
2016-12-14郑志东袁红刚王雯雯陶欢
郑志东 袁红刚 王雯雯 陶欢
(北方电子设备研究所, 北京 100191)
非均匀杂波背景下双基地MIMO雷达距离扩展目标的GLRT检测
郑志东 袁红刚 王雯雯 陶欢
(北方电子设备研究所, 北京 100191)
利用球不变随机矢量(Spherically Invariant Random Vector,SIRV)描述非均匀杂波,建立了双基地多输入多输出(Multiple-Input Multiple-Qutput,MIMO)雷达距离扩展目标的信号检测模型,提出了距离扩展目标的两步广义似然比检测(Generalized Likelihood Ratio Test,GLRT)算法.首先,根据目标散射系数的两种假设模型,分别推导确定型目标、高斯型目标GLRT检测器的解析表达式,然后利用固定点迭代算法估计杂波协方差矩阵,获得自适应GLRT(AD-GLRT和AG-GLRT)检测器.仿真实验表明:AD-GLRT和AG-GLRT检测器的检测性能均优于非均匀杂波背景、高斯杂波背景下点目标的检测性能,且两者的检测性能相当,并且虚拟阵元数、目标分布的距离单元数,以及信杂比越大,两者的检测性能越好.
双基地MIMO雷达;非均匀杂波;距离扩展目标;广义似然比
DOI 10.13443/j.cjors.2015121101
引 言
近年来,多输入多输出(Multiple-Input Multiple-Output, MIMO)雷达[1]引起了国内外学者的极大关注,它利用多个发射天线同时辐射相互正交或者不相关信号,并通过接收匹配滤波器组分离出不同天线的发射信号,从而获得检测性能、估计精度、杂波抑制等方面的优势.MIMO雷达按照发射和接收阵元的配置形式,可分为:统计MIMO雷达[2-3]和单(双)基地MIMO雷达[4-7].统计MIMO雷达有利于获得空间分集增益,提高雷达的检测性能和角度估计精度[2-3];而单(双)基地MIMO雷达利用波形分集增益扩展阵列的孔径自由度,提高雷达的参数估计精度,增强杂波的抑制能力[8],本文针对非均匀杂波背景下双基地MIMO雷达的距离扩展目标检测问题进行研究.
现有关于MIMO雷达检测的研究主要集中于高斯噪声(杂波)假设条件下[2, 9-10].然而,当目标具有较小擦地角或者MIMO雷达具备较高距离分辨单元时,杂波回波将在距离向上产生起伏,此时高斯模型不再成立,表现为概率密度函数具有较长拖尾的非均匀杂波.对于非均匀杂波,大多采用球不变随机矢量(Spherically Invariant Random Vector, SIRV)描述其统计特性[11],文献[12]提出了SIRV杂波模型下MIMO雷达的自适应广义似然比-线性二次(Adaptive Generalized Likelihood Ratio-Linear Quadratic Test,AGLR-LQT)算法检测,但该算法在参考单元数较少情况下,检测性能下降较快.为克服上述不足,文献[13]提出了全数据广义似然比检测(Full Data Generalized Likelihood Ratio Test, FDGLRT)方法,利用固定点迭代算法估计杂波协方差矩阵和目标复振幅,该方法在参考单元数据较短时,其检测性能优于AGLRT-LQ,在参考数据充足时,两者具有相同的检测性能,但该方法需要进行多次迭代,计算量较大.
上述关于非均匀杂波MIMO雷达检测的文献,均假设目标处于一个距离单元内.然而,当雷达发射端发射距离向高分辨信号(如不同频带的线性调频信号组)时,飞机、舰船等目标尺寸远大于雷达的单个距离分辨单元,此时目标的回波不再完全处于一个距离单元内,而是分布在不同的距离单元之中,形成距离扩展目标.此时,如果仍采用单个距离单元的检测方法进行目标检测,将会因目标信息利用不全、目标邻近单元信号污染[14]等问题使得检测性能急剧下降.目前,关于非均匀杂波背景下MIMO雷达的距离扩展目标检测问题还并未报道过,本文基于双基地MIMO雷达体制,分析SIRV杂波模型下距离扩展目标的检测性能.首先给出距离扩展目标下双基地MIMO雷达的信号模型,然后根据目标假设模型的不同,分别推导了确定型和高斯型目标的广义似然比检测(Generalized Likelihood Ratio Test,GLRT)检测性能,仿真实验验证了理论分析的有效性.
1 问题描述
双基地MIMO雷达系统及距离扩展目标如图1所示.考虑M发N收的双基地MIMO雷达,发射和接收阵元间隔为Δtλ和Δrλ.所需检测的距离扩展目标可以利用多个强散射点近似,并且可以认为扩展目标的回波为这些强散射点回波的叠加[14].

图1 距离扩展目标下双基地MIMO雷达收发配置图
假设距离扩展目标跨越H个距离单元,目标的能量在其跨越的距离单元内均匀分布,每个距离单元内的强散射点为pl(l=1,…,H)个,各个距离单元内的散射点经历方位向扩展(发射角和接收角方向).如图1所示,假设第l个距离单元中第k个散射点所对应的雷达发射角和接收角分别为φl,k,θl,k(k=1,…,pl),其散射系数为αl,k.假设发射端发射正交信号,则t时刻接收端接收到的第l个距离单元内的回波信号为

(1)

=[B(φl)⊙A(θl)]αl+cl.
(2)
式中: ⊙表示矩阵的Khatri-Rao积; αl=[αl,1,…,αl,pl]T为第l个距离单元内的散射系数矢量; B(φl)=[b(φl,1),b(φl,2),…,b(φl,pl)]和A(θl)=[a(θl,1),a(θl,2),…,a(θl,pl)]分别为第l个距离单元内散射点的发射方向矩阵和接收方向矩阵; cl为MN×1的非均匀杂波,本文采用文献[11]中的球不变随机矢量模型来描述非均匀杂波,该模型能够与大量实测杂波数据吻合,且模型中的每个参数具有明确的物理意义.假设各个距离单元内的杂波cl相互独立,则第l个距离单元的非均匀杂波可以用如下的乘积模型表示:

(3)
式中: 散斑分量xl为零均值、归一化协方差矩阵为Ml的复高斯随机矢量,假设每个距离单元内的散斑分量统计独立,且具有相等的协方差矩阵,统一记为M; τl为第l个距离单元内的杂波纹理分量,该纹理分量在不同距离单元上是一个概率密度函数为p(τ)的非负一维随机变量,它代表了该单元的杂波功率大小.
由上述假设可知: H0情况下,接收信号的回波为杂波分量;H1情况下,其回波为含有杂波的目标信号.令Kl=B(φl)⊙A(θl)∈CMN×pl,则非均匀杂波背景下,距离扩展目标的检测问题可归结为如下的二元假设检验:
(4)
式中,yl为MN×1的匹配滤波输出矢量.对于目标的散射系数αl,可以有两种假设方式[15]: 1) 确定型散射系数模型,即αl为确定的未知参量; 2) 随机型散射系数模型,并假设其服从复高斯随机分布,即αl~Nc(0,Σl).在不同的散射系数模型下,其接收数据的统计特性不同,从而使得检测器的结构也不同,因此本文对这两种目标模型下的检测性能进行逐一讨论.
根据奈曼-皮尔逊准则,利用似然比检验可以得到最优的检测方案,但对于式(4)的假设检验而言,由于检测过程中存在未知参数(散射系数αl,杂波的纹理分量τl均未知),似然比(Likelihood Ratio Test,LRT)无法得到一致最优势检验.为此,本文采用两步GLRT方法推导非均匀杂波条件下距离扩展目标的自适应检测性能,其基本步骤为:首先假设杂波协方差矩阵已知,利用最大似然估计出未知参数的估计值,得到GLRT准则下目标的检测器结构,然后利用辅助距离单元数据求得杂波协方差值,并代替先前假设已知的协方差值,得到距离扩展目标的自适应检测器.同时,由于本文主要研究距离扩展目标下的检测算法,因此假设各个强散射点的方向矢量Kl(信号子空间)以及维数pl已知.在实际应用中,维数pl可以利用阵列信号处理中信源数目估计的方法得到,方向矢量Kl也可以利用子空间估计类算法[4-7]求得.以下利用GLRT检测方法分别推导出确定型目标(Deterministic Target Model)和高斯型目标(Gaussian Target Model)的检测器表达式(分别简记为D-GLRT和G-GLRT).
2 GLRT检测器设计
2.1 确定型目标GLRT检测器(D-GLRT)
令L=MN,假设目标的散射系数αl为确定的未知参量,则H0情况下观测数据服从yl~Nc(0,τl,0M),H1情况下观测数据服从 yl~Nc(Klαl,τl,1M),且由于yl(l=1,…,H)在各个待检测的距离单元之间相互独立,因此可得H0/1情况下L×H维观测矩阵Y=[y1,…,yH]的联合条件概率密度:
(5)
e-(yl-Klαl)HM-1(yl-Klαl)/τl,1.
(6)


(7)
对式(7)中的αl求偏导可得

(l=1,…,H).
(8)
同理可得H0/1情况下,各个距离单元的纹理分量估计值:
(9)


(10)
将式(8)和(9)代入式(10),可得检测器的似然比为
ΛD=lnΛD(Y)

(11)

(12)
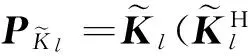
2.2 高斯型目标GLRT检测器(G-GLRT)

(13)
由此可知,G-GLRT检测器的似然比为
(14)

(15)
=-LHln(1-pl/L)-
(16)
在上述讨论中,假设散斑分量x的协方差矩阵M为已知量,但实际中M需要估计得到.假设在H0情况下,接收端接收到Lr组辅助数据y(l),由此可以采用文献[12]中的固定点算法进行迭代求解协方差矩阵M的估计值,即
(17)
3 计算机仿真
本节通过实验仿真验证AD-GLRT和AG-GLRT算法的目标检测性能.假设杂波协方差矩阵已利用固定点算法估计得到(即为自适应检测),并分别对式(12)和式(16)采用蒙特卡洛(Monte-Carlo)实验计算虚警概率和发现概率,为了尽可能消除仿真实验的随机性对检测性能的影响,估计每个Pfa和Pd的仿真次数分别为100/Pfa和105次,实验时假设虚警概率为10-5.考虑M发N收的双基地MIMO雷达,收发阵元间隔为50倍波长配置(使得目标经历方位向扩展),假设杂波服从K分布,杂波多普勒频谱的平均值为0,散斑分量的协方差矩阵为空间色噪声,其第(p,q)元素为M(p,q)=ρ|p-q|ejπ(p-q)/2,其中相关系数ρ=0.7,杂波的纹理分量服从Gamma分布,其杂波分布的尖锐程度由形状参数v决定,v越小,杂波出现的尖峰越多,非高斯特征越明显.根据以上假设,进行如下实验.
实验1 不同检测器之间的性能比较.考虑2发4收的MIMO雷达,距离扩展目标占据的距离单元数为H=4,辅助数据单元数Lr=8H,各个距离单元内散射点的个数及收发角度如表1所示.将D-GLRT和G-GLRT的检测性能与文献[12]中非均匀杂波下点目标检测器,文献[2]高斯杂波下点目标检测器的检测性能进行比较.仅距离扩展目标检测器假设目标只存在距离向上的扩展,而不存在方位向上的扩展,即满足pl=1(l=1,…,H),此时假设目标的收发角度为(30°,15°).点目标检测器假设目标均不存在距离向和方位向扩展,即目标只占据一个距离单元.图2示出了四种不同检测器的检测概率随信杂比(Signal-to-ClutterRatio,SCR)的变化曲线,实验时杂波的形状参数v=0.7.

表1 H=4时各个散射点的分布及收发角度值

图2 不同检测器的检测概率随SCR的变化曲线
由图2可知,D-GLRT与G-GLRT的检测性能优于非均匀杂波下点目标,以及高斯杂波下点目标检测器的检测性能.这是由于:目标在方位和距离向上的扩展可以减小目标的闪烁起伏,利于更好地辩分出目标与杂波的频谱,同时,目标建模为在距离向和方位向同时扩展更加符合实际情况,减少了由于建模而引起的误差,所以其检测概率有所提高.此外,比较确定型目标的D-GLRT和随机型目标的G-GLRT,可以发现,两者具有类似的检测性能.因此在以下实验中仅对D-GLRT的检测性能进行分析.
实验2 虚拟孔径数以及距离单元数对D-GLRT检测性能的影响.假设虚拟孔径数L为变化参数,其它仿真条件同实验1,图3给出了不同L下D-GLRT的发现概率随SCR的变化曲线,实验时目标的参数取值见表1.图4为不同距离单元数H情况下D-GLRT的检测概率随SCR的变化曲线,实验中H=2,4,6时各散射点的角度参数取值分别见表1至表3,在进行不同距离单元检测性能比较时,目标的总能量保持不变,且能量均匀分布于各个距

图3 不同孔径下检测概率随SCR的变化曲线

图4 不同距离单元下检测概率随SCR的变化曲线

距离单元12散射点发射角φ{32°,35°}{30°,32°,34°}散射点接收角θ{17°,15°}{16°,17°,13°}散射点数目p23
离单元以及各散射点上,实验时辅助数据单元数目为48.
由图3可知,阵元虚拟孔径数越大,D-GLRT的检测性能越强,这是由于在目标散射点数目相同时,提高孔径数L,能够提高最大似然估计以及杂波协方差的估计精度,同时确保了信号和杂波子空间的充分分离,因此检测器的检测性能不断改善.由图4可知,增加距离单元个数,也可以提高D-GLRT的检测性能,但随着距离单元数的不断增加,检测性能的提升程度变缓(即:单元数从2增大到4获得的提升性能大于由4增大到6的提升性能).其主要原因为:当增加距离单元数目时,虽然减少了目标回波的闪烁起伏,但同时也增大了杂波能量的积累,引起积累的增益损失.当距离单元内信杂比有明显优势时,距离分辨单元数目的增加,可以降低目标回波的起伏,进而改善目标的检测性能;而当两者的能量相当时,继续增大距离分辨单元数,将增加杂波能量的积累,引起积累损失,进而使得检测性能的改善效果不明显.因此随着H的增加,检测性能的提升程度将变缓.
实验3 杂波形状参数对D-GLRT检测性能的影响.考虑2发4收的双基地MIMO雷达,目标占据的距离单元个数H=4,辅助数据单元数目Lr=8H,图5为不同杂波形状参数v情况下D-GLRT的检测概率随SCR的变化曲线.由图5可知,杂波越尖锐(v越小),GLRT-LQ的检测概率越高.该结论与文献[14]中传统高分辨雷达距离扩展目标检测的结论相一致.

表3 H=6时各个散射点的分布及收发角度值

图5 不同杂波形状参数下D-GLRT检测概率随SCR变化曲线
4 结 论
本文研究了非均匀杂波环境下双基地MIMO雷达的距离扩展目标检测问题.以SIRV杂波为假设模型,建立了双基地MIMO雷达的距离扩展目标检测模型,并将目标的散射系数分为确定型和随机型两种,分别推导出了确定型目标GLRT检测器(D-GLRT)和高斯型目标GLRT检测器(G-GLRT)的表达式,并利用固定点迭代算法估计出杂波协方差矩阵,得到距离扩展目标的自适应检测器(AD-GLRT和AG-GLRT).仿真实验表明:AD-GLRT检测器和AG-GLRT检测器的检测性能均优于非均匀杂波和高斯杂波背景下点目标的检测性能,且两者具有相似的检测性能.AD-GLRT检测器的检测概率随着虚拟孔径数、目标跨越的距离单元数,以及SCR的增大而增大.本文在估计杂波协方差矩阵M时,主要采用辅助数据进行估计,为了进一步充分利用目标信号的数据,可以考虑将待检测单元数据和辅助数据相结合进行杂波协方差矩阵估计,该问题将在下一步研究中重点探讨.
附录A

(A1)

(A2)


(A3)
将式(A2)和式(A3)代入式(15),并取对数运算后可得

(A4)


(A5)
又由于H0情况下,观测数据Y的条件概率密度为

(A6)
因此,由式(A5)和式(A6)可得二元检测的对数似然比:

(A7)
[1] TANG B, NAGHSH M M, TANG J. Relative entropy-based waveform design for MIMO radar detection in the presence of clutter and interference[J]. IEEE transactions on signal processing, 2015, 63(14): 3783-3796.
[2] SUN B, CHEN H W, WEI X Z, et al.. Power allocation for range-only localisation indistributed multiple-input multiple-output radar networks—a cooperative game approach [J]. IET radar sonar navigation, 2014, 8(7): 708-718.
[3] HAIMOVICH A M, BLUM R S, LENARD J, ET AL. MIMO radar with widely separated antennas[J]. IEEE signal processing magazine, 2008, 25(1): 116-129.
[4] TANG B, TANG J, ZHANG Y, et al. Maximum likelihood estimation of DOD and DOA for bistatic MIMO radar[J]. Signal processing, 2013, 93(5): 1349-1357.
[5] HONG J, ZHANG J K, WONG K M. Joint DOD and DOA estimation for bistatic MIMO radar in unknown correlated noise[J]. IEEE transactions on vehicular technology, 2015, 64(11): 5113-5125.
[6] 樊劲宇, 顾红, 苏卫民, 等. 基于张量分解的互质阵MIMO雷达多目标参数估计方法[J]. 电子与信息学报, 2015, 37(4): 933-938.
FAN J Y, GU H, SU W M, et al. Co-prime MIMO radar multi-parameter estimation based on tensor decomposition[J]. Journal of electronics & information technology, 2015, 37(4): 933-938.(in Chinese)
[7] XIA T Q. Joint diagonalization based DOD and DOA estimation for bistatic MIMO radar[J]. Signal processing, 2015, 108: 159-166.
[8] CHEN C Y, VAIDYANATHAN P P. MIMO radar space-time adaptive processing using prolate spheroidal wave functions[J]. IEEE transactions on signal processing, 2008, 56(2): 623-635.
[9] WANG J, JIANG S, HE J, et al. Adaptive detectors with diagonal loading for airborne multi-input multi-output radar[J]. IET radar sonar and navigation, 2009, 3(5): 493-501.
[10] MAIO D, LOPS M. Design principles of MIMO radar detectors [J]. IEEE transactions on aerospace and electronics systems, 2007, 43(3): 886-898.
[11] CONTE E, LONGO M. Characterisation of radar clutter as a spherically invariant random process[J]. IEE proceedings, 1987, 134(2): 191-197.
[12] CHONG C Y, PASCAL F, OVARLE Z P. MIMO radar detection in non-gaussion and heterogeneous clutter[J]. IEEE journal of seleted topics in signal processing, 2010, 4(1): 115-126.
[13] CHAO S Y, CHEN B X. FDGLRT detector of MIMO radar in non-homogeneous clutter [J]. Electronics letters, 2011, 47(6): 403-404.
[14] CONTE E, MAIO A D, RICCI G. CFAR detection of distributed targets in non-gaussian disturbance[J]. IEEE transactions on aerospace and electronics systems, 2002, 38(2): 612-621.
[15] VAN TREES H L. Optimum array processing: detection, estimation, and modulation theory[M]. New York: John Wiley & Sons, 2002.
[16] JIN Y W. Adaptive detection of distributed signals using sensor arrays[D]. Santa Cruz: University of California, 1996.

郑志东 (1985-),男,福建人,博士,工程师,主要研究方向为MIMO雷达技术、雷达信号处理、阵列信号处理.
袁红刚 (1972-),女,陕西人,硕士,高级工程师,研究方向为雷达信号处理.
GLRT-based detection algorithm for range-spread targets of bistatic MIMO radar in nonhomogenous clutter
ZHENG Zhidong YUAN Honggang WANG Wenwen TAO Huan
(InstituteofNorthElectronicEquipment,Beijing100191,China)
The signal detection model of range-spread target of bistatic multiple-input multiple-output(MIMO) radar is formulated by using the spherically invariant random vectors(SIRV) to describe the non-homogenous clutter. A two-step generalized likelihood ratio test(GLRT) detector algorithm is proposed for detecting the range-spread target. Two different assumptions are made concerning the radar cross section(RCS) coefficient of target: either modeled as deterministic unknown or as Gaussian parameter. Then the GLRT detectors for range-spread target are derived under these two hypotheses. It shows that both detectors lead to the similar results for range-spread target, and the proposed detector enables a detection performance enhancement over that of the point target detectors in the both non-homogenous and Gaussian clutters. Furthermore, the detection performance of both the proposed detectors increases as the virtual aperture number, the target range cell number and the Signal Clutter Ratio (SCR) increase.
bistatic MIMO radar; nonhomogenous clutter; range-spread target; generalized likelihood ratio test (GLRT)
10.13443/j.cjors.2015121101
2015-12-11
TN957
A
1005-0388(2016)04-0803-08
郑志东, 袁红刚, 陶欢, 等. 非均匀杂波背景下双基地MIMO雷达距离扩展目标的GLRT检测 [J]. 电波科学学报,2016,31(4):803-810.
ZHENG Z D, YUAN H G, TAO H, et al. GLRT-based detection algorithm for range-spread targets of bistatic MIMO radar in nonhomogenous clutter[J]. Chinese journal of radio science,2016,31(4):803-810. (in Chinese). DOI:10.13443/j.cjors.2015121101
联系人: 郑志东 E-mail:focusdong@aliyun.com
