基于GPU的并行FDTD方法在二维粗糙面散射中的应用
2016-12-14贾春刚郭立新刘伟
贾春刚 郭立新,2 刘伟
(1.西安电子科技大学物理与光电工程学院,西安 710071;2.西安电子科技大学综 合业务网理论及关键技术国家重点实验室,西安 710071)
基于GPU的并行FDTD方法在二维粗糙面散射中的应用
贾春刚1郭立新1,2刘伟1
(1.西安电子科技大学物理与光电工程学院,西安 710071;2.西安电子科技大学综 合业务网理论及关键技术国家重点实验室,西安 710071)
利用显卡(Graphics Processing Unit, GPU)加速时域有限差分(Finite-Difference Time Domain,FDTD)法计算二维粗糙面的双站散射系数,介绍了FDTD的理论公式以及计算模型.采用各向异性完全匹配层(Uniaxial Perfectly Matched Layer,UPML)截断FDTD计算区域.重点讨论了基于GPU的并行FDTD计算粗糙面双站散射系数的并行设计方案计算流程.在NVIDIA GeForce GTX 570 显卡上获得了50.7×的加速比.结果表明:通过对FDTD计算粗糙面散射问题的加速,极大地提高了计算效率.
时域有限差分法;GPU;并行;粗糙面散射
DOI 10.13443/j.cjors.2015111801
引 言
由于在遥感、目标识别与雷达探测等领域的重要应用,随机粗糙面统计特性的研究具有重要的意义[1-2].FDTD在解决粗糙面散射问题中具有其自身的优势:粗糙面不论是介质还是导体,只需设置好粗糙面的介电参数即可;对于单层或是多层粗糙面散射问题,统一对粗糙面建模进行处理而不需类似矩量法更改积分方程[3].然而FDTD计算粗糙面散射问题尤为耗时,特别是计算二维粗糙面散射,并且在计算随机粗糙面散射时,至少要取20个粗糙面样本,因此限制了FDTD大部分都应用在一维粗糙面散射中.因此,对FDTD计算粗糙面散射问题进行加速很有必要.李娟等利用基于消息传递接口(Message Passing Interface,MPI)计算机集群对其进行加速,得到了较高的加速比[4].这种方法的缺点是硬件消耗很大.
近些年来,自从英伟达推出CUDA(Compute Unified Device Architecture)构架以来,可编程GPU在计算电磁学领域得到了广泛的应用.马韬等利用GPU加速高阶矩量法计算电大尺寸目标的散射问题[5].文献[6]中,GPU被用来加速计算二维时域有限元的辐射问题,并取得了4倍多的加速比.张波等利用 NVIDIA GT130M GPU加速计算FDTD方法[7].文献[8]中,并行FDTD程序相对CPU串行程序和8个CPU核的MPI并行程序,分别获得了超过8倍和1.5倍的加速.近期,GPU在加速计算随机问题中也有应用:在文献[9]中,GPU用来加速四路径结合互易性定理计算由地面、树干和树叶组成的三层模型,并取得了294倍的加速比;文献[10]利用GPU加速FDTD计算一维粗糙面与目标复合散射问题,并进行了一系列的优化.因此,本文利用GPU强大的并行计算能力进一步地对二维随机粗糙面散射问题进行加速.本文中GPU和CPU平台的计算精度均为单精度.
1 FDTD计算二维粗糙面散射

exp[j(Kmkxm+Knkyn)].
(1)
式中:
F(Kmk,Knk)= 2π[LxLyW(Kmk,Knk)]1/2·
(2)
M和N分别为 x和 y方向离散的点的个数; N(0,1)为一组服从正态分布的随机数; W(Kmk,Knk)为功率谱密度函数,本文研究的是高斯分布的随机粗糙面,功率谱密度函数为

(3)
式中: lx和ly分别为沿x和y方向的相关长度; δ为均方根高度,它们决定了高斯粗糙面的轮廓起伏.
图1中,FDTD的计算区域被划分成多个子区域.为了在有限计算区域模拟开域情况,在FDTD计算网格最外面加入虚拟吸收边界,本文使用UPML来截断FDTD计算网格[11].图1中,ABCD为总场/散射场边界,它将散射场从总场中分离出来,并且在此引入入射波[11].近场迭代完成之后,再外推边界A′B′C′D′做近远场变换,以获得远场的双站散射系数(Bistatic Scattering Coefficient,BSC),
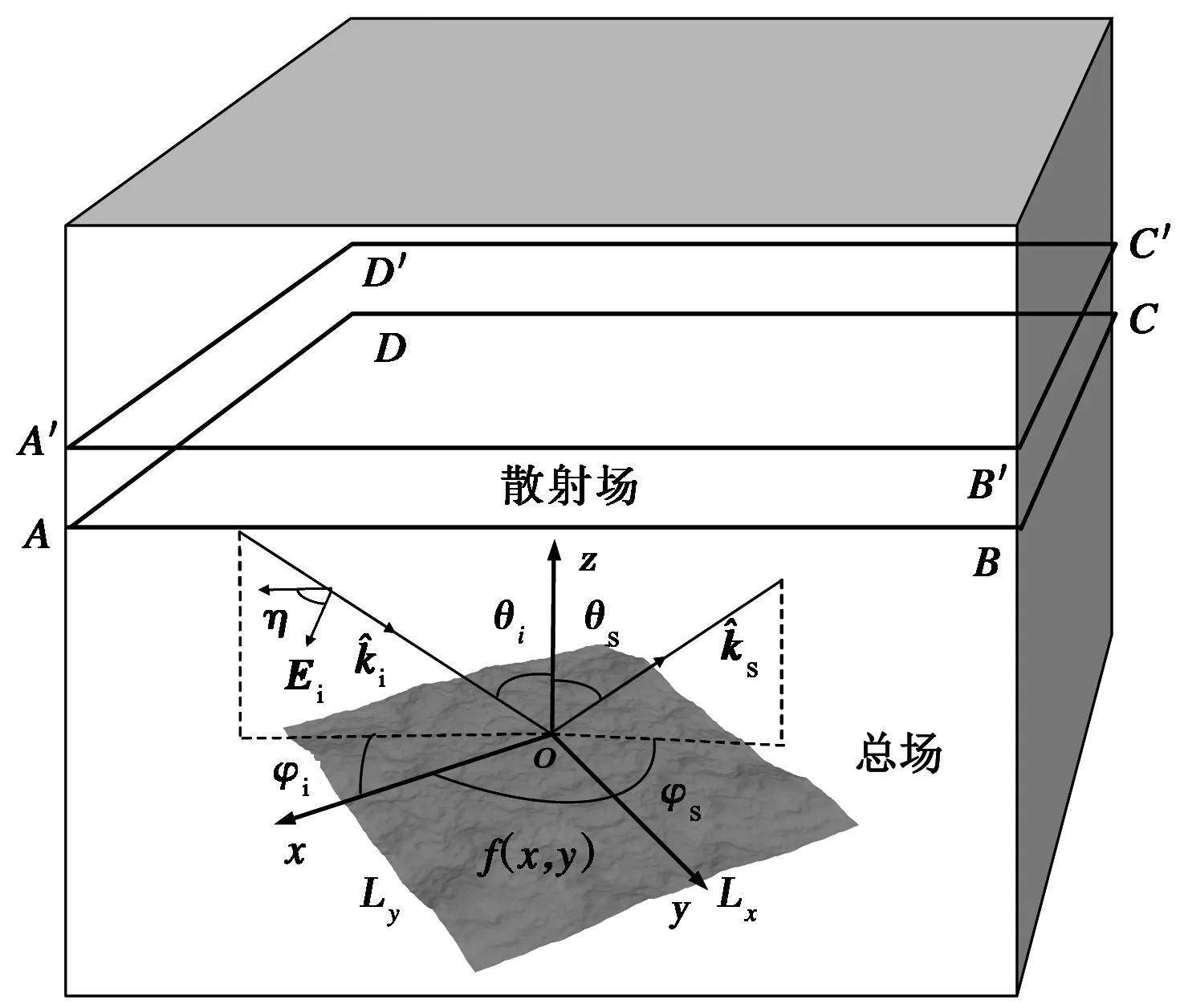
图1 二维粗糙面几何模型

(4)
式中: Es为远区散射场; Ei为入射场; S为粗糙面面积.
2 GPU并行方案
2.1 计算平台
本节将重点阐述FDTD计算二维粗糙面散射的CUDA并行实现方式.并进一步对并行程序进行优化以提高计算效率.C程序在Intel Core Quad Q8200 CPU上运行,核函数在NVIDIA GeForce GTX 570 显卡上执行,具体的参数如表1所示.

表1 计算平台具体参数
2.2 并行计算流程
图2给出了基于GPU的并行FDTD计算二维粗糙面散射的计算流程图.首先根据粗糙面的尺寸分配内存、显存,并对其初始化FDTD迭代参数并设置UPML.然后进入时间步的循环,入射电场、入射磁场的迭代.由于近场迭代部分非常耗时,因此并行化设计在近场迭代部分进行.当磁场分量迭代时,其所需要的电场分量要保证已经全部迭代完成,同样,当电场分量更新时,其所需要的磁场分量也要保证迭代完成.这需要在整个网格内对电场、磁场分量进行同步,重新调用核函数强制同步.本文使用两个核函数来实现近场迭代功能:eupdatekernel()和hupdatekernel(),分别负责电场的迭代和磁场的迭代.当近场迭代完成之后,将近远场外推时所需要的近场分量Ex,Ey,Hx,Hy从GPU端传回到CPU端以计算远场双站散射系数.

图2 计算流程图
3 数值结果与分析
为了确保FDTD方法的准确性和稳定性,空间和时间步长分别取Δx=Δy=Δ=λ/10和Δt=0.5×Δ/c.其中,λ为入射波波长,c为自由空间中的光速.为了很好地吸收外行波,UPML吸收边界层厚度取10Δ,本文将分别从计算准确性和计算效率两个方面对并行算法加以讨论.
图3比较了并行FDTD与串行FDTD计算二维粗糙面的双站散射系数.其中高斯粗糙面的尺寸为S=Lx×Ly=3.84 m×3.84 m,相关长度lx=ly=0.1 m,均方根高度为δ=0.01 m.入射频率f=1.0 GHz,入射角为θi=45°,入射方位角为φi=0°.如图3中所示,对于四种极化的结果来说,两者方法吻合得很好,这证明了并行FDTD计算二维粗糙面双站散射系数的准确性.
表2给出了并行FDTD和串行FDTD分别计算不同FDTD网格的加速比.保持粗糙面尺寸S=Lx×Ly=3.84 m×3.84 m不变,网格数分别为128Δ×128Δ,256Δ×256Δ,512Δ×512Δ,其他参数与上例相同.从表中可以看出,加速比随未知量增加而增大,增大到一定程度减小.最大加速比为50.7×.

表2 CPU与GPU计算时间比较

(a) VV极化 (b) HV极化
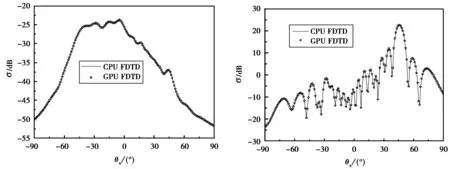
(c) VH极化 (d) HH极化图3 CPU FDTD和GPU FDTD结果对比
4 结 论
基于GPU的并行FDTD算法用来研究二维粗糙面散射问题.在前面工作的基础上[4,9],进一步利用GPU进行加速,并将研究的问题从一维粗糙面散射扩展到了更具有实际应用价值的二维粗糙面情况.2个核函数用来实现算法的并行化,同时给出了并行程序的计算流程.通过与传统的串行FDTD算法结果相对比,验证了本文算法的正确性.通过与串行FDTD在计算不同网格数时的计算时间的比较,验证了本文算法的计算效率.最终,得到了最大为50.7×的加速比.但由于计算机内存以及显卡显存的限制,二维粗糙面的计算尺寸还不够大,因此,今后的工作重点将利用硬盘缓存技术,提高算法计算二维粗糙面的电尺寸.
[1] 姬伟杰, 童创明. 二维海面上舰船目标电磁散射及合成孔径雷达成像技术研究[J]. 物理学报, 2012, 61(16): 1603011-1603018.
JI W J, TONG C M. Research on electromagnetic scattering computation and synthetic aperture radar imaging of ship located on two-dimensional ocean surface[J]. Acta physica sinica, 2012, 61(16): 1603011-1603018. (in Chinese)
[2] 王蕊,柴水荣,郭立新,等.介质涂覆机翼与下垫粗糙面后向复合散射研究[J].电波科学学报,2014,29(6):1051-1056.
WANG R, CHAI S R, GUO L X, et al. The study of the scattering from a dielectric coated airfoil above a rough surface[J]. Chinese journal of radio science, 2014,29(6):1051-1056. (in Chinese)
[3] KUANG L, JIN Y Q. Bistatic scattering from a three-dimensional object over a randomly rough surface using the FDTD algorithm[J]. IEEE transactions on antennas and propagation, 2007, 55(8): 2302-2312.
[4] LI J, GUO L X, ZENG H. FDTD method investigation on the polarimetric scattering from 2-D rough surface[J]. Progress in electromagnetics research, 2010, 101: 173-188.
[5] 马韬, 陈明生, 吴先良, 等. 基于GPU加速的高阶矩量法研究与应用[J]. 微波学报, 2013, 29(4): 34-37.
MA T, CHEN M S, WU X L, et al. Research and application of the high-order method of moments based on GPU acceleration[J]. Journal of microwaves, 2013, 29(4): 34-37. (in Chinese)
[6] 刘昆, 王晓斌, 廖成,等. 图形处理器(GPU)加速时域有限元的二维辐射计算[J]. 电波科学学报, 2008, 32(1): 111-114.
LIU K, WANG X B, LIAO C, et al. Acceleration of time-domain finite element 2-D radiation using graphics processor units(GPU)[J]. Chinese journal of radio science, 2008, 32(1): 111-114.(in Chinese)
[7] 张波, 薛正辉, 任武, 等. 基于图形处理器的时域有限差分算法研究[J]. 电波科学学报, 2011, 26(1): 108-112.
ZHANG B, XUE Z H, REN W, et al. Acceleration of FDTD algorithm based on GPU computing[J]. Chinese journal radio science, 2011, 26(1): 108-112. (in Chinese)
[8] 邵宗有, 王昭顺, 刘新春,等.基于CPU-GPU异构机群的FDTD并行算法加速研究[J].系统仿真学报,2013,25(2):235-240.
SHAO Z Y, WANG Z S, LIU X C, et al. Accelerating parallel FDTD on CPU-GPU heterogeneous cluster system[J]. Journal of system simulation, 2013,25(2):235-240. (in Chinese)
[9] JIANG W Q, ZHANG M, CHEN H, et al. CUDA implementation in the EM scattering of a three-layer canopy[J]. Progress in electromagnetics research, 2011, 116: 457-473.
[10] JIA C G, GUO L X, YANG P J. EM scattering from a target above a 1-D randomly rough sea surface using GPU-based parallel FDTD[J]. IEEE antennas and wireless propagation letters, 2014, 14: 217-220.
[11]葛德彪, 魏兵. 电磁波时域计算方法——时域积分方程法和时域有限差分法[M]. 西安: 西安电子科技大学出版社, 2014: 126-205.
GPU-based FDTD method for analysis of electromagnetic scattering from a 2D rough surface
JIA Chungang1GUO Lixin1,2LIU Wei1
(1.SchoolofPhysicsandOptoelectronicEngineering,XidianUniversity,Xi’an710071,China; 2.StateKeyLaboratoryofIntegratedServicesNetworks,XidianUniversity,Xi’an710071,China)
In this paper, graphics processing unit (GPU)-accelerated finite-difference time domain (FDTD) is developed to expedite the calculation of bistatic scattering coefficient of a two dimensional (2D) rough surface. The formulae and computation model are introduced, respectively. The FDTD lattices are truncated by a uniaxial perfectly matched layer (UPML). The implement of GPU-based FDTD for calculation of electromagnetic scattering from a 2D rough surface is discussed in detail, and the calculation process is also given. Finally, speedup of 50.7×is obtained on NVIDIA GeForce GTX 570 GPU after optimization. The proposed parallel FDTD algorithm improves the computational efficiency greatly.
FDTD; GPU; parallel; rough surface scattering
10.13443/j.cjors.2015111801
2015-11-18
国家杰出青年科学基金(61225002); 航空科学基金与航空电子系统射频综合仿真航空科技重点实验室联合资助(20132081015) 联系人: 贾春刚 E-mail: cgjia@stu.xidian.edu.cn
TN011
A
1005-0388(2016)04-0683-05
贾春刚 (1986-),男,吉林人,博士研究生,研究方向为粗糙面及其与目标的并行加速计算.
郭立新 (1968-),男,陕西人,西安电子科技大学物理与光电工程学院教授,研究方向为电磁/光波在复杂介质中的传播和散射.
刘伟 (1979-),男,陕西人,西安电子科技大学副教授,主要研究方向为电磁散射、微波遥感与参数反演.
易建新 (1989-),男,湖南人,硕博生连读,研究方向为雷达系统建模与信号处理.
贾春刚, 郭立新, 刘伟. 基于GPU的并行FDTD方法在二维粗糙面散射中的应用[J]. 电波科学学报,2016,31(4):683-687.
JIA C G,GUO L X,LIU W. GPU-based FDTD method for analysis of electromagnetic scattering from a 2D rough surface [J]. Chinese journal of radio science,2016,31(4):683-687. (in Chinese). DOI: 10.13443/j.cjors.2015111801
