非线性检测方法检测微弱信号的检测频率范围分析
2016-12-14张斌辉张翠侠
刘 燕,张斌辉,张翠侠
(1.宿州学院 煤矿机械与电子工程研究中心,安徽 宿州 234002;2.国家中小型轴承产品质量监督检验中心,浙江 绍兴 312500)
非线性检测方法检测微弱信号的检测频率范围分析
刘 燕1,张斌辉2,张翠侠1
(1.宿州学院 煤矿机械与电子工程研究中心,安徽 宿州 234002;2.国家中小型轴承产品质量监督检验中心,浙江 绍兴 312500)
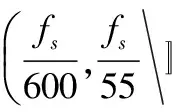
混沌振子;差分振子;采样频率;待测频率
特征信号淹没在背景噪声特性不明的情况,一直是信号处理的难题。传统检测方法旨在对噪声进行消除或抑制的方法,但当噪声频率与信号频率接近或者相等时,滤除噪声的同时微弱信号也受到了极大的损害,因此能检测的最低信噪比很高,微弱信号的检测受到了限制。现在,无论从深度还是高度上,非线性理论的研究都成为人们为了解决信号处理的难题必须研究的内容。混沌振子[1-3]、差分振子[4-6]、随机共振[7,8]等非线性动力学现象的发现使微弱信号的处理上了新的台阶。无论是混沌振子还是差分振子研究很多学者的研究成果都是针对检测器中涉及的参数选取,很少有人针对混沌振子和差分振子可以检测的待测频率的范围进行研究,文献[9]证明了随机共振方法检测的待测频率的范围和采样频率有一定的关系,本文运用仿真的方法得出了混沌振子和差分振子检测的上下限频率,当采样频率一定的条件下,混沌振子有最高检测频率,差分振子有最低检测频率,只有待检测频率在混沌振子和差分振子所要求的范围内,才能正确合理的使用混沌振子和差分振子方法检测微弱信号。
1 混沌振子
混沌振子检测来源于弹簧振动模型的Duffing方程[10](P47-50),是一个二阶微分方程,通常用来检测微弱正弦信号的Duffing方程形式:
(1)
其中k为阻尼比,取k=0.5;-x3+x5为非线性恢复力;fcos(t)内置信号。
令 t=w0τ,可以推出任意频率的周期信号的检测数学模型[11]:
(2)
当加入外部周期信号时,式(2)变为
(3)
式中:w0为内部周期摄动力的频率,w1为待测微弱周期信号的角频率,θ为被测周期信号的相位,N(t)为随机噪声[12]。
2 采样频率对混沌振子检测方法影响
混沌振子检测微弱信号频率,通过四阶Runge-Kutta法解算混沌振子方程,由于Runge-Kutta法是一种迭代算法,采样频率直接影响了迭代步长,当步长选取不同时,从连续系统导出的离散系统也不同,由于步长不同,从混沌态过渡到大尺度周期状态的阈值也不相同。步长越小,离散系统越接近实际的连续系统,所以工程实际中要合理的选用采样频率。使用混沌振子检测微弱信号时,步长最大能选取多少才不使离散系统偏离实际系统呢?也就是当采样频率一定的情况下,混沌振子能够检测的下限频率是多少呢?我们通过下面的仿真实验来寻找。
设待测信号:
s(t)=0.05cos(2π·40·t)
(4)
将待测信号代入到式(3)中,即
(5)
对式(5)采用4阶Runge-Kutta算法进行求解,取初始值x(0)=1,y(0)=1,k=0.5,数据长度N=9 216,采样频率fs=4 000。计算得到混沌振子的阈值fb=0.522 6。设置f=0.5,因为f+0.05>0.522 6,所以混沌振子脱离混沌状态,从系统输出的相轨迹图检测已知频率的微弱信号,如图1所示。
通过仿真发现,针对式(5),当其他参数不变,采样频率减小时,由混沌状态转变为大尺度周期状态的阈值也会随之减小,我们逐渐减小采样频率fs的值,对于同一个待检测微弱信号,理论上duffing振子相图肯定会处于大周期状态的。仿真如下图2所示,相位图的变化趋势大致是:大尺度周期状态→粗糙的大尺度周期状态(图d)→超大数值状态(图f),当相位图呈现直线形式时,无法观察到混沌振子的变化,这种情况是无法进行信号检测的。为了找出检测频率和采样频率之间的关系,在粗糙的大尺度周期状态和超大数值两种状态之间进行仿真,在2 300Hz和2 000Hz之间对采样频率进行细化,相图结果如图2(e)所示。从图2(e)可以看出,两种状态之间还会出现混沌状态。
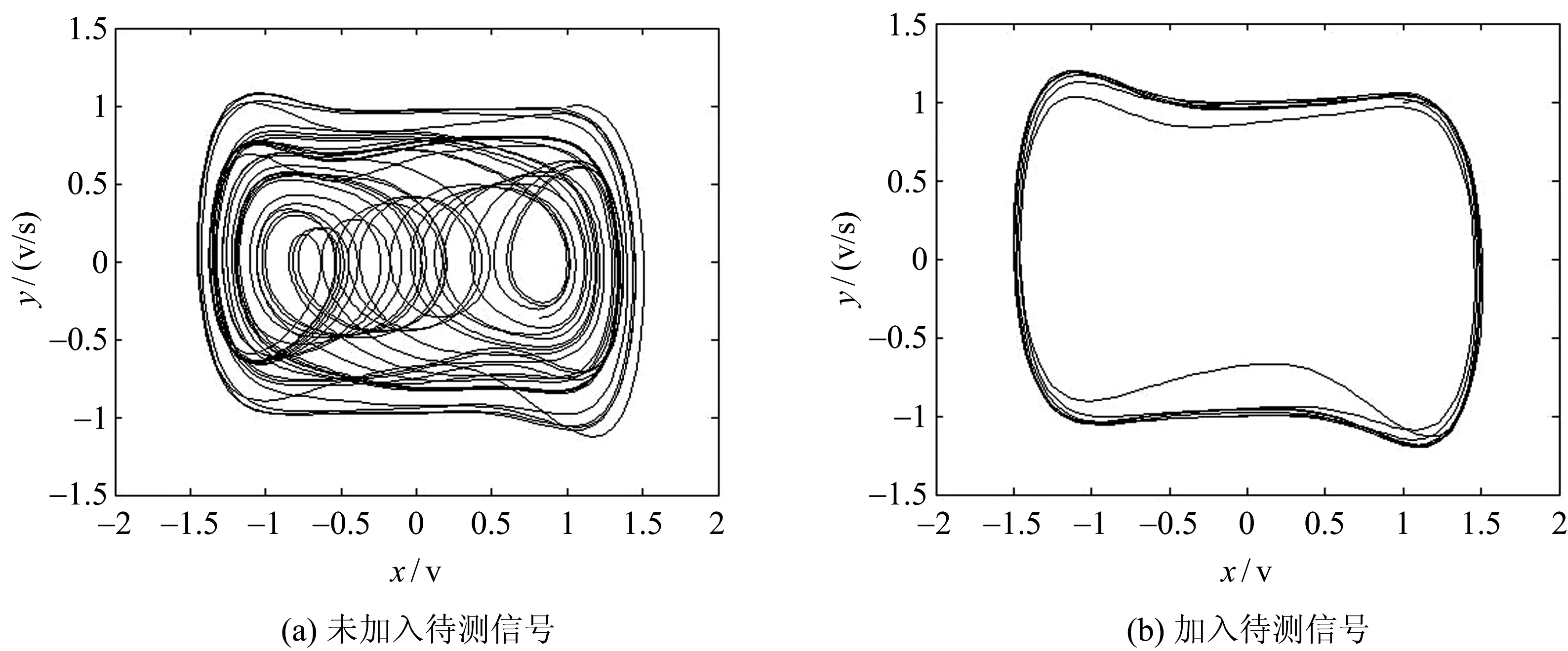
图1 不同状态下的混沌振子相图
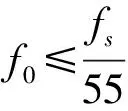
3 差分振子检测器
差分振子检测器是以二元差分方程为基础构造的检测器[13],具体数学模型如下
(6)
令α=-(a+d),β=ad-bc,f(k)=bpcos(2kπfe+2kπfd/fs),则 (6)式可简化为
xk+2+αxk+1+βxk=f(k)T(k)
(7)
式中:a,b,c,d为差分振子的系统参数;p为放大倍数;fd为待检测频率;fe为系统激励频率;fs为输入信号的采样频率;T(k)为输入信号。
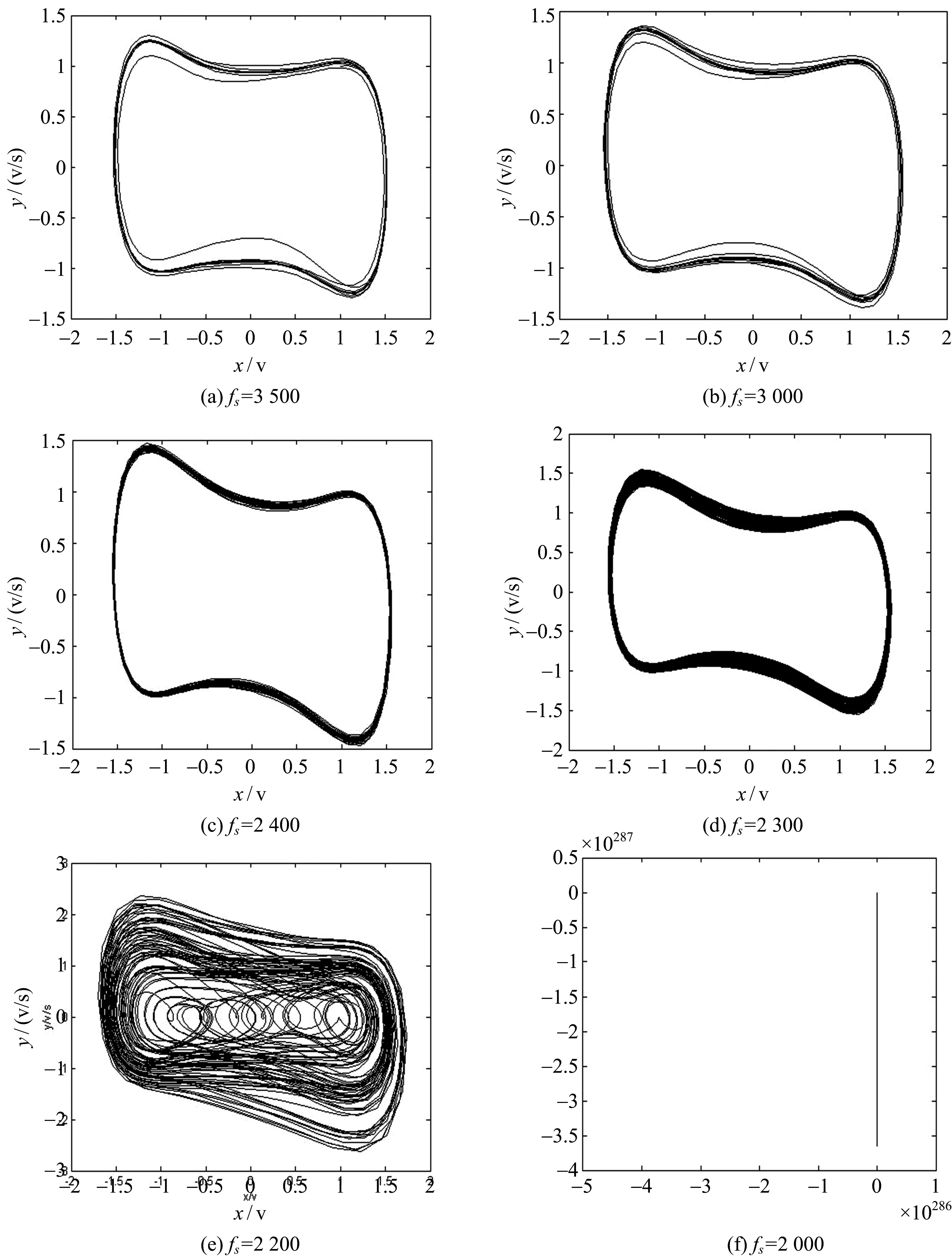
图2 不同采样频率下的混沌振子状态
4 采样频率对差分振子检测方法影响
差分振子的检测方程中包含了信号的采样频率这一信息,那么,在应用差分振子对信号进行检测时,采样频率和检测频率之间需要满足什么样的关系,才能有效地检测微弱信号将在本节中进行阐述。通过构造仿真信号来寻找采样频率和检测频率之间的关系。
构造仿真信号:
T(k)=0.1·sin(2kπ·17)+g·randn(length(k))
(8)
利用差分振子对得到的一系列的数值序列进行检测。差分振子的参数设置如下:a=0.03;b=1.0;c=-1;d=-1;x(1)=6;y(1)=6;fe=0.3319;fd=17;fs=1000;p=1;g=0.1。
因此,为了满足采样定理,采样频率从70 Hz开始,依次取500 Hz、3 000 Hz、6 000 Hz、10 000 Hz、12 000 Hz,得到的差分振子相图如图3所示。从图3中可以看出,当差分振子相图取70 Hz时,相图很清晰的收敛于极环,随着采样频率增大,极环面积逐渐减小,当采样频率大于10 000 Hz,已经观察不到极环了,空白区域逐渐被填满。所以,使用差分振子检测微弱信号时,信号的采样频率不能过高,这样就会导致结果的不准确。
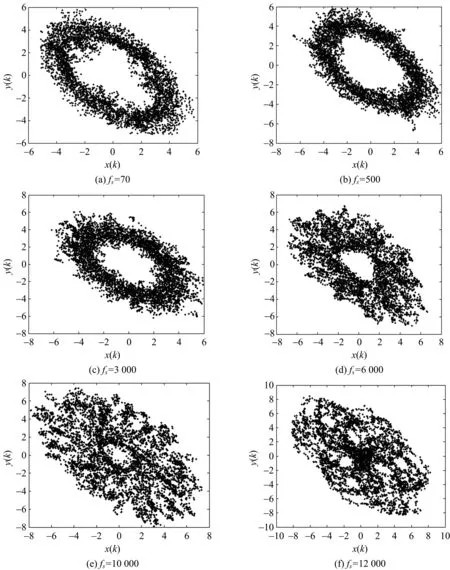
图3 不同采样频率下的差分振子状态
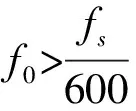
为了证明上述结论,构造仿真信号:
将仿真信号首先输入到混沌振子检测器中,取初始值x(0)=1,y(0)=1,k=0.5,数据长度N=9 216,采样频率fs=4 000。混沌振子检测待检测频率fs=50Hz的阈值fb=0.473 6,取f=0.44,将待测信号加入到混沌检测系统中,如图所示,待检测频率等于50Hz的时候可以正确检测出来,但是不能正确地识别出80Hz的微弱信号。
此时将待测信号输入到差分振子检测系统,差分振子的参数设置如下:a=0.03; b=1.0; c=-1; d=-1; x(1)=6;y(1)=6;fe=0.331 9;fs=1 000; p=1;g=0.1,fd分别取50Hz和80Hz的时候,如图(a)和(b)所示。此时两个待检测频率分别检测出来。
5 结论
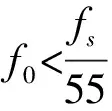

图5 差分振子相图
[1]陈伟根,云玉新,杜林,等.基于互相关和李雅普诺夫指数的微弱正弦信号[J].混沌检测电力系统自动化,2008,32(18):44-48.
[2]王娜,郑德忠.基于混沌振子的低信噪比语音端点检测新方法[J].仪器仪表学报,2009,30(7):1432-1435.
[3]何金群,胥永刚,崔玲丽,等.基于不变矩的DUFFING相位图的自动识别[J].噪声与振动控制,2008,5(10):80-82.
[4]胥永刚,冯明时,谢志聪,等.差分振子检测器输出特性研究及应用[J].振动与冲击,2012,13(19):57-60.
[5]马朝永,王克,胥永刚,等.差分振子时间历程在微弱调制信号检测中的应用[J].噪声与振动控制,2013,33(6):148-152.
[6]胥永刚,马海龙,付胜,等.机电设备早期故障微弱信号的非线性检测方法及工程应用[J].振动工程学报,2011,24(5):529-538.
[7]Gammaitoni L, Hanggi P, Jung P, Marchesoni F. Stochasticresonance[J]. Rev. Mod. Phys, 1998, 70(1): 223-287.[8]Yong-gang Leng, Tai-yong Wang, Yan Guo. Engineering Signal Processing Based on Bistable Btochastic Resonance[J]. Machanical Systems and Signal Processing, 2007,21(01):138-150.
[9]冷永刚.大信号变尺度尺度随机共振的机理分析及其工程应用研究[D].天津:天津大学(博士学位论文),2004.
[10]刘秉正,彭建华.非线型动力学[M].北京:高等教育出版社,2004:47-50.
[11]王冠宇,陶国良.混沌振子在强噪声背景信号检测中的应用[J].仪器仪表报,1997,18(2):209-212.
[12]Wang Guanyu, Wei Zheng, He Sailing. Estimation of Amplitude and Phase of a Weak Signal by Using the Property of Sensitive Dependence on Initial Conditions of a Nonlinear Oscillator[J]. Signal Processing, 2002,82(1):103-115.
[13]李楠,赵东成,李虹波,等.电机转子系统早期故障可视化检测的差分振子法[J].电力自动化设备,2007,27(6):74-77.
Analysis on Detection Frequency Range for Detecting Weak Signal with Nonlinear Detection Method
LIU Yan1, ZHANG Binhui2, ZHANG Cuixia1
(1.MechanicalandElectronicEngineeringResearchCenterforCoalMine,SuzhouUniversity,Suzhou234002,China;2.NationalBearingProductsTestCenter,Shaoxing312500,China)
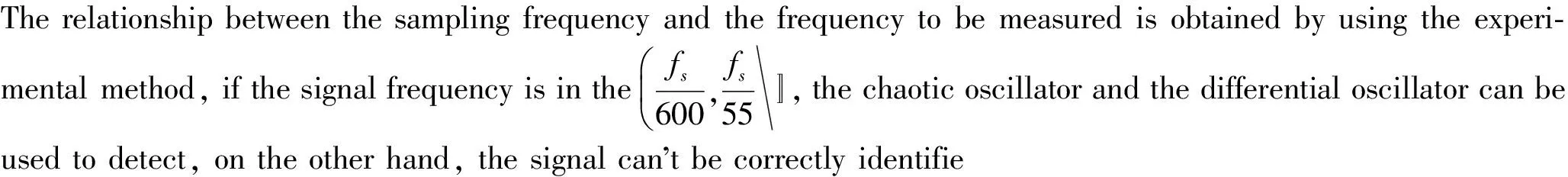
chaotic oscillator; differential oscillator; sampling frequency; test frequency
2016-05-22
安徽省高校自然科学研究项目(KJ2016A776);宿州学院煤矿机械与电子工程研究中心开放课题资助(2014YKF16)。
刘燕(1987-),女,安徽宿州人,助教,硕士,研究方向:设备故障诊断。
TN
A
