基于改进的多目标混合遗传算法区域水资源供需的研究*
——以中国山东省为例
2016-12-13葛福婷芦小乐朱家明
葛福婷,张 秀,芦小乐,朱家明
(安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030)
基于改进的多目标混合遗传算法区域水资源供需的研究*
——以中国山东省为例
葛福婷,张 秀,芦小乐,朱家明
(安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030)
针对世界性水资源短缺及水资源优化配置的问题,选取严重缺水的中国山东省作为研究对象,通过定量分析、相关分析、变量控制等方法,建立了水资源供需时间序列回归模型和多目标线性规划遗传算法模型,得知供水能力表达及预测,山东省未来15年水资源将中度缺水(供水能力为0.6422~0.9791),并据此制定水资源干扰计划,合理有效缓解水资源短缺现状.
水资源短缺;多元时间序列分析;多目标混合遗传算法;灵敏度分析;LINGO
0 引言
根据联合国的统计,全球有16亿人(占世界人口的四分之一)缺水[1],随着经济的发展和人口的增加,人类对水资源的需求不断增加,再加上存在对水资源的不合理开采和利用,很多国家和地区出现不同程度的缺水问题[2].依据联合国缺水地图,选择了严重缺水的中国山东省作为研究地区,对定量探究水资源短缺的成因、预测未来水资源的可用性、提出缓解或解决对策具有重要意义.
1 山东缺水现状及影响因素分析
1.1 山东省水资源短缺现状
近年来,通过对山东省水资源的调查评价,得知全省水资源总量多年平均为345亿立方米,其中地表水为264亿立方米,地下水为163亿立方米,两者之间在一定条件下可以互相转化的重复计算量为82亿立方米.从降水资源、地表水资源、地下水资源及山东省最大的客水资源——黄河水资源四个方面概括总结山东省水资源的特点,主要有:总量不足,人均占有量少;单位面积占有量少;年际、年内变化剧烈;地区分布不均等.
1.2 山东省水资源短缺主要影响因素
在合理的假设下,我们得出结论,影响水资源短缺的因素包括水资源需求总量因素和水资源供给量因素.其中水资源需求总量的因素有:生活需水量、生态需水量、农业需水量、工业需水量.影响水资源供应总量的因素有:地表水资源供给总量、地下水资源供给总量、海水利用、污水回收利用,由于数据的搜集难度和重要程度,这里只考虑前两个因素.
详细的,可进一步划分水资源供给和需求为水源地和用户.其中水源包括地下供水源、地表供水源、外调水和污水回用,用户包括生活区、生态区、工业区和农业区.同时,出于水资源调配的目的,考虑到可持续发展,建立区域水资源优化配置的三大目标:经济目标(即区域供水带来的直接经济效益最大)、社会目标(即总缺水量最小)和环境目标(即区域内重要污染物排放量最小).
2 数据的获取和假设
数据源于2016美国大学生数学建模IMC E题[3].为便于解决问题,提出如下假设:1)对水资源的需求的研究仅考虑生活、生态、工业和农业需水;2)对水资源的供给的研究仅考虑地下水供给、地表水供给、海水利用和污水回收利用;3)针对供给水源的顺序,优先考虑水供水的用户;4)水资源分配给每个用户的系数相当合理;5)针对中国山东省水资源状况所做的研究,所选取的指标具有代表性和时间序列性;6)存在人为修改数据,修改幅度较小.
3 水资源供需状况分析
3.1 模型的建立
3.1.1 构建水资源供需函数
依据中国统计年鉴[4]中山东省水资源状况的相关指标,选取影响水资源需求的4项指标ydi(i=1,2,3,4)[分别指生活、生态、工业、农业需水量]和水资源供给的2项指标 ysj(t)(j=1,2)[分别指地表、地下供水量],作为影响山东省水资源供给能力的评估准则.分别求解该地区水资源总需求量和总供给量的时间序列函数关系:
yd=yd1(t)+yd2(t)+yd3(t)+yd4(t);
ys=ys1(t)+ys2(t)
3.1.2 构建供水能力指标及隶属函数
水资源供求比λ=ys/yd,显然,λ越大表明供水能力越好.依据水资源供需比值大小的区间,可划分不同供水分级标准以衡量供水能力大小,见表1.

表1 水资源供求比
依据表1,为定量化表达并预测该地区供水能力大小,建立不同水资源供应程度的隶属函数:
(1)
(2)
(3)
(4)
(5)
其中,μk(λ)(k=1,2,3,4,5)分别表示过度缺水、重度缺水、中度缺水、轻度缺水和水源充足五种水源状态下的隶属度函数,可用于衡量供水能力大小.
3.2 模型的求解
查阅中国统计年鉴,考虑简化模型和数据获取的难易,得到近10年山东省水源状况的主要影响指标,见表2.其中影响水资源供给的指标主要为地表供水量和地下供水量,影响水资源需求的指标主要为生活需水量、生态需水量、工业需水量和农业需水量.
根据表2中的数据,运用STATA软件编程,分别多次结合多函数形式迭代拟合,得到各指标的最优时间序列函数,分别加总整理得
yd=yd1+yd2+yd3+yd4=0.8662t+0.2578t2+0.0610t3+225.5722 (R2=0.875)
(6)
ys=ys1+ys2=-7.8832t+0.8493t2+0.0354t3+13.9874 ln t+220.3785 (R2=0.834)
(7)
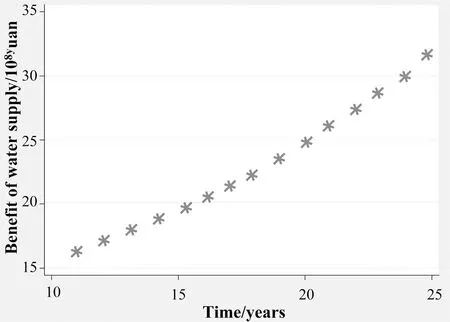
其中,R2表示可决系数,且0 表2 山东省近10年水资源短缺主要影响指标数据 参照模型的建立中的水资源供求比:λ=ys/yd,通过拟合λ的时间序列函数并进一步代入μk(λ)(k=1,2,3,4,5),遵循隶属度值最大原则(即同一年份的供求比若求得多组隶属度值则以最大值表示最优),整理得山东省未来15年的水资源供水能力,见表3. 依据表3知:山东省未来15年将逐渐处于中度缺水状态(这里,水资源供求比区间为0.8463~0.9125,中度缺水),供水能力大小区间为0.6422 ~ 0.9791.这里的μmax数值越大表示供水能力越强,相应地缺水程度越弱,而μmax总体上呈先增加再减小(在2018年达到最大供水能力0.9791,2029年供水能力最低,为0.6422)的动态变化,即水资源短缺状况先是有所缓解然后又慢慢加剧了. 表3 山东省未来15年供水能力 3.3 模型的分析 综上分析,预测山东省未来15年将处于中度缺水的状态(水资源供求比区间为0.8463~0.9125,供水能力为0.6422~0.9791),不过这种缺水状态处于一种动态的变化,即先有所缓解后而又加剧了水资源短缺的现状,可能是由于水资源管理疏忽、节水措施不普及等原因造成的.同时,预测2015-2019年间水资源需求总量与供给总量差距越来越大,即水资源短缺进一步恶化.针对上面所研究的水资源供需状况,宏观上了解了水资源短缺的现状及预测未来水资源状态,为进一步提出建设性的节水计划——水资源优化调配方案奠定了理论基础. 4.1 模型的建立 联系中国统计年鉴和南水北调的相关数据,另又搜集反映水资源供给量的指标:外调水和污水回用量,进一步补充模型建立的完整性和可靠性.以经济、社会和环境的综合效益最优为目标,并运用混合遗传模拟退火算法[6],建立如下初始目标函数[7]: (8) 其中,f1(x)表示经济目标,xij,xcj,xdj,xej分别为地下供水源、地表供水源、外调水源、污水回用向山东j用户的供水量;bij,bcj,bdj,bej为水源向用户供水的效益系数;cij,ccj,cdj,cej为水源向用户供水的费用系数;αi,αc,αd,αe为水源的供水次序系数;βj为用户的用水公平系数. (9) 其中,f2(x)表示社会目标,Dj为用户需水量. (10) 其中,f3(x)表示环境目标,pj为用户排放重要污染物的浓度;qj为用户的污水排放系数. 同时,针对多目标混合遗传算法进一步的优化,得到改进的多目标混合遗传算法模型,试建立相关供水约束条件如下: a)可供水量约束:(见式(11)). b)输水能力约束:(见式(12)).式中,W为水源的最大输水能力. (11) (12) c)需水量约束: Djmin≤xij+xcj+xdj+xej≤Djmax (13) 式中,Djmin、Djmax分别为山东地区j用户的最小、最大需水量. (14) 总量控制: (15) e)变量非负约束:模型中涉及的所有变量均大于或等于零. 4.2 模型的求解 以2014年山东省水资源的相关数据为研究对象,重点分析调运方案.运用LINGO软件编程求解: f1(x)=0.1831x11+0.0808x12+0.1726x13+ 0.0644x14+0.0620x21+0.0330x22+0.0454x23+ 0.0178x24-0.0041x31+0.0101x32+0.0498x33+ 0.0130x34-0.0108x41+0.0067x42+0.0184x43+ 0.0013x44 (16) f2(x)=220.245-(x11+x12+x13+x14+ x21+x22+x23+x24+x31+x32+x33+x34+x41+x42+x43+x44) (17) f3(x)=0.0486(x11+x21+x31+x41)+ 0.0011(x12+x22+x32+x42)+0.2219(x13+x23+x33+x43)+0.0180(x14+x24+x34+x44) (18) 其中变量xmn表示m水源地向n用水部门的供水量,m=1,2,3,4分别表示地下供水源、地表供水源、外调水和污水回用四个水源地 ,n=1,2,3,4分别表示用水部门为生活区、生态区、工业区和农业区. 基于模型的建立中的约束条件和山东省水资源相关数据,运用LINGO软件,建立线性规划并求解.整理得2014年的最优调配方案为: x11=33.31,x13=19.06,x14=58.57,x22=6.76,x23=9.79,x24=70.30,x34=15.45,x44=6.67,x12=x21=x31=x32=x33=x41=x42=x43=0,f1(x)=15.2899,f2(x)=0.3214,f3(x)=10.7482. 同理,可以算出2004到2013年的最优调运方案. 查阅相关资料及文献,得到山东省近10年三大目标变量及水资源总需求量数据,运用STATA软件,多重函数迭代拟合后,得到三个目标下的最优时间序列函数: y1=1.0814lnt+0.0279t2+10.4375 (19) y2=0.1837lnt+0.5468 (20) y3=-0.9309lnt-0.0299t2-0.4260sint+15.5165 (21) 其中,y1,y2,y3分别表示水资源优化配置后的经济效益、总缺水量、重要污染物排放量时间序列函数.据原始数据和式(19)~ (21)拟合出近10年及未来15年的三大目标的变化趋势(以经济效益为例). 分别对比水资源优化配置后近10年和未来15年的三大目标效益走势(如图1、2的经济效益目标),易知:水资源优化配置后,山东省未来15年的经济效益呈递增趋势,且递增的速率增大;总缺水量也呈递增的趋势,但递增的速率稍稍减缓;重要污染物排放量呈递减的趋势,且递减速率呈“不变→减缓→增加→不变→减缓”的变化趋势,说明水污染得到足够的缓解.综上,采取水资源优化配置后,山东省未来水资源的可用性增强,且对水资源短缺的敏感性相对减弱. 0.0354t3+13.8037lnt+219.8317 (22) 图1 近10年山东省水资源优化配置后经济效益 图2 未来15年山东省水资源优化配置后经济效益 4.3 模型的分析 综上,易知:基于山东省水资源相关数据,结合模型的建立中改进的多目标混合遗传算法的三大目标函数和五大约束条件,得到最优的水资源调配方案(例:2014年山东省水资源最优调配方案),在水资源优化配置之后,山东省缺水状况将得到有效解决,水资源的供给与需求基本呈均衡状态. 此外,山东省未来水资源的可用性(即在水资源需求总量不断加剧的现状下,水资源的供给总量得到稳步的增加)增强,且对水资源短缺的敏感性相对减弱.在不考虑其他变动因素的假设前提下,一定时期内,实施了优化配置的水资源调运方案后,水资源短缺可以得到有效缓解.同时,可对其他地区的水资源调配提供定量、可靠的调运方案,以求改善水资源短缺现状,也可为暂时水资源充足或濒临水资源短缺地区提供理论支持及水资源短缺的预防方案. 全文针对严重缺水的中国山东省水资源短缺的现状展开研究,从对水资源供需现状的分析及预测、水资源调运优化配置方案的分析,分别在宏观和微观上展示了水资源短缺的现状及弥补水资源短缺的优化调运方案.所预测的未来水资源状况及供水能力,提出的水资源优化配置方案,具有较强的合理性和广泛的适用性,可以很好地推广到其他区域的水资源研究,不仅可以为水资源短缺地区提供很好的改善方案,也为暂时水资源充足或濒临水资源短缺地区提供了水资源短缺的预防方案和理论支持;同时,也警示在城市化和社会化不断加剧的社会现状下,其他国家或地区也应重视水资源短缺现状,采取相关措施及方案,谨防在不久的将来水资源短缺成为世界性关键议题的发生. [1]全球水资源现状[EB/OL].http://www.gezhi.sh.cn/zuoping/renxuan/sheng.htm. [2]水资源短缺[EB/OL].http://baike.haosou.com/doc/6277112-6490550.html. [3]2016美国大学生数学建模IMC E题.我们朝着干渴的星球迈进吗[EB/OL].http://blog.sciencenet.cn/blog-752541-953146.html. [4]中华人民共和国国家统计局[EB].http://www.stats.gov.cn/tjsj/ndsj/. [5]周玉玺,葛颜祥,周霞.区域水资源供求失衡及解决机制研究[J].水资源与水工程学报,2010,21(1):13-15. [6]周丽,黄哲浩,贺惠萍.多目标非线性水资源优化配置模型的混合遗传算法[J].水电能源科学,2015,23(5):22. [7]王瑞霞,钱龙霞,许新宜.基于模糊概率的水资源短缺风险评价模型及其应用[J].水利学报,2009,40(7):813-814. [责任编辑 苏 琴] [责任校对 黄招扬]The Supply and Demand of Regional Water Resources based on Improved Multi-Objective Hybrid Genetic Algorithm——of China's Shandong Province as an Example GE Fu-ting ,ZHANG Xiu ,LU Xiao-le ,ZHU Jia-ming (SchoolofStatisticsandAppliedMathematics,AnhuiUniversityofFinanceandEconomics,Bengbu233030,China) In this article,we mainly study the problem of worldwide water scarcity and the method of optimizing allocation of water resource.By means of selecting an area severely lacking water-Shandong province of China as the research object,we established a time series regression model of supply and demand of water resources and a multi-objective linear programming and genetic algorithm model.Then we concluded that there will remain a status of moderate shortage of water (the capacity of supplying water is 0.6422 ~ 0.9791)over the next 15 years in Shandong province,and accordingly formulated the interference plan of water resources. Water resources shortage; Multivariate time series analysis; Multi-objective hybrid genetic algorithm; Sensitivity analysis; LINGO 2016-05-20. 国家自然科学基金(11301001);安徽省创新创业项目(AH201410378258). 葛福婷(1995-),女,安徽舒城人,安徽财经大学统计与应用数学学院研究生,研究方向:经济统计. 朱家明(1973-),男,安徽泗县人,安徽财经大学统计与应用数学学院副教授,研究方向:应用数学与数学建模. X24,X321 A 1673-8462(2016)03-0068-05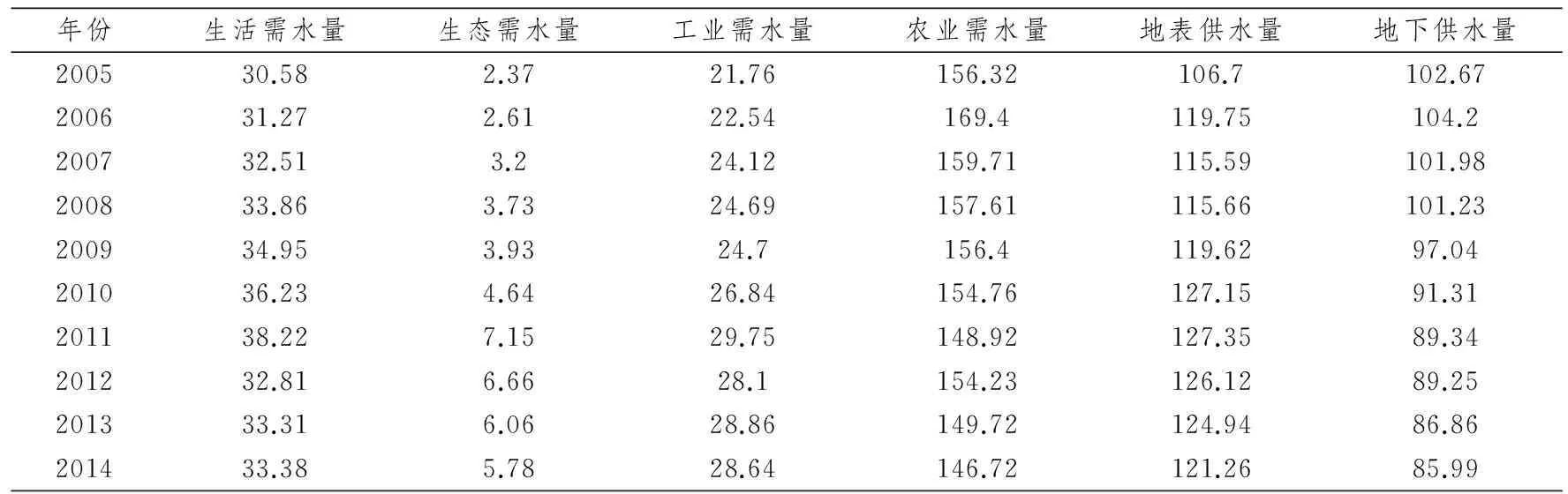

4 水资源调运优化配置方案

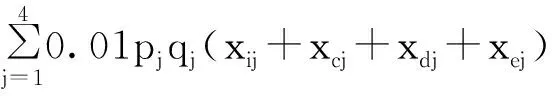


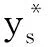
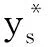

5 结语
