基于机会约束规划的海水淡化优化调度

梁立达，王 剑，孙贵根

(杭州电子科技大学自动化学院，浙江 杭州 310018)



基于机会约束规划的海水淡化优化调度

梁立达，王 剑，孙贵根

(杭州电子科技大学自动化学院，浙江 杭州 310018)

针对海水淡化系统优化调度中存在的不确定性，利用随机模拟技术建立了基于机会约束规划的系统动态调度模型，给出了其经济目标函数与约束条件，并采用粒子群算法对优化问题进行了求解.通过与冗余算法比较表明，机会约束规划算法在求解精度上有明显优势，但是其求解速度慢于冗余算法.

海水淡化；不确定性；优化调度；机会约束规划；粒子群算法；随机模拟

0 引 言

图1 并联式反渗透海水淡化工程结构图

海水淡化系统优化调度能有效地降低制水成本，达到节能的目的.文献[1]研究了反渗透海水淡化系统的多目标优化问题，在优化过程中考虑了投资与运营成本、能源回收与水回收率和环境等性能指标，采用多目标优化方法对系统进行优化调度.文献[2]利用边界简约技术，解决了特定水质条件下反渗透系统最优结构和操作条件的非突优化问题，有效提高了算法的收敛速度.文献[3]在海水淡化研究过程中，以操作费用最小为目标函数，以开放方程描述的各模型方程为约束，以设备和产品质量限制为边界条件，采用联立求解技术将微分代数方程组成的优化问题转化成NLP问题进行优化求解.文献[4]依据海水淡化厂投资折旧成本和产水操作费用，建立了以24小时为一个周期的海水淡化经济模型，同时考虑了不同水质、不同温度等因素，分别利用差分进化算法和有限元分解对系统进行优化调度.上述研究未考虑不确定性对调度问题的影响，无法直接应用于实际.本文重点讨论了市政供水预测误差这个随机变量对经济目标函数的影响，建立了基于机会约束规划的调度模型，并利用粒子群算法对其进行求解.

1 膜法海水淡化优化调度模型

反渗透海水淡化工程结构图如图1所示.整个海水淡化工程由取水单元系统、预处理系统、反渗透系统和后处理系统组成.一个制水车间由n台产水机组组成，每个产品水池由nj台产水机组负责产水，由m个产品水池统一负责向市政供水.

2 机会约束规划模型

机会约束规划是随机规划理论的重要分支，主要解决约束条件中含有随机变量优化问题，其优化理念是允许所做的决策在一定的程度上不满足约束条件，但该决策应该使约束条件成立的概率不小于某一置信水平[5].对于极小化问题，其一般的模型如下：

(1)

2.1 市政供水量预测偏差描述

(2)

2.2 经济调度模型

在机会约束条件下，确定以一个周期内生产市政所需供水量的能耗费用为目标函数：

(3)

式中：f为海水淡化能耗费用，K(此处取24)为优化周期，C(k)为k时刻电价，γ为能耗与制水量关联系数，Qi(k)为机组i在k时刻的产水量.

2.3 约束条件

上述经济调度模型的约束条件包括设计约束和技术约束，主要有：

1)目标函数的机会约束条件

(4)

2)供水需求机会约束条件为

(5)

(6)

3)产品水池容量约束条件为

(7)

(8)

4)机组产水量约束条件为

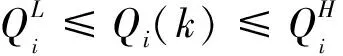
(9)

表示机组i在k时刻受产水量上下限约束.

3 模型求解

3.1 PSO算法理论

粒子群算法(Particle Swarm Optimizer， PSO)通用性强、群体搜索并具有记忆能力，保留局部个体和全局种群的最优信息，具有较强的鲁棒性.其速度更新公式如下：

(10)

3.2 算法流程

图2 算法流程图

机会约束规划最有效的求解方式是将其转化成等价类进行求解，但这种求解方法只针对特殊情况下的机会约束规划问题[7]，上述涉及的规划问题无法转化为等价类进行求解.本文采用PSO算法嵌入蒙特卡罗随机模拟对其进行求解.PSO嵌入蒙特卡罗随机模拟算法流程如图2所示.相关步骤如下：

1)读取相关数据.包括市政供水量预测值及预测偏差的概率分布，其设计约束和技术限制、粒子群算法参数与置信水平；

2)初始化种群与粒子初速度；

3)利用随机模拟的悲观值估计法计算每个粒子适应值；

4)粒子状态的更新.将最新适应值(局部最优值)和局部最优值(全局最优值)比较，若较好，则替换，否则保持原有位置不变；

5)粒子的进化.按照式(10)进行粒子的迭代与更新；

6)对更新后的粒子再次利用随机模拟概率估计法验证是否满足约束条件并检验粒子可行性.若可行，则替换否则保持原有位置；

7)重复步骤3～6直至最大迭代数，程序结束.

4 算例分析

4.1 随机模拟技术法求解

本文用到反渗透工程对象的参数(包括分时电价表)见文献[4].市政供水预测表和PSO算法参数表分别见表1和表2.表3是条件约束置信水平β1=0.9时，制水能耗随着目标函数置信水平α变化的数据.表4是目标函数置信水平α=0.9时，制水能耗随着条件约束置信水平β1变化的数据.

表1 市政供水量预测表

表2 算法参数表

表3 β1取0.9时不同α优化方案比较

表4 α取0.9时不同β1优化方案比较

从表3和4中可以看出，制水能耗和置信水平呈递减关系，即随着置信水平的增加，制水能耗在减小.这是与实际相符合的.机会约束规划置信度水平(α，β1)反应了调度方案的风险程度.置信水平越小，调度结果更优，经济效益更好.但违反约束的概率越大，伴随着系统风险的增加.因此，决策者在实际调度过程中需要考虑经济效益和风险程度的平衡，选取合适的置信水平.

4.2 冗余技术法模型求解

(11)

将处理微小不确定性干扰的两种方式进行比较，采用java语言在Myeclipse10编程，运行环境为HP desktop6300MT 台式机(CPU主频3.2 GHz，内存4 GB)，运行仿真程序500次，平均求解结果比较如表5所示.

表5 两种调度方案比较

从表5中可以看出，从经济角度考虑，用随机模拟技术处理预测误差的效果明显优于冗余技术，随机模拟技术求解结果平均值比冗余技术求解结果平均值减少7 445.7元，从优化求解时间上看，随机模拟技术平均优化时间慢于冗余技术约178.08 s.

5 结束语

本文根据市政供水预测误差，建立了基于机会约束规划的系统动态调度模型，给出了其经济目标函数与约束条件，并采用粒子群算法对模型进行优化求解.调度方案的优劣取决于多方面因素，如市政供水量的预测、海水淡化系统中的其他随机变量等，这些难点将会是下一步研究的重点.

[1]VINCEF,MARECHALF,AOUSTINE,etal.Multi-objectiveoptimizationofROdesalinationplants[J].Desalination, 2008, 222(1):96-118.

[2]MARCOVECCHIOMG,AGUIRREPA,SCENNANJ.Globaloptimaldesignofreverseosmosisnetworksforseawaterdesalination:modelingandalgorithm[J].Desalination, 2005, 184(1/3):259-271.

[3]江爱朋，程文，王剑，等.全流程卷式反渗透海水淡化系统操作优化[J].化工学报,2014,65(4):1333-1343.

[4]王剑．大规模反渗透海水淡化工程调度问题研究及应用[D].杭州:浙江大学,2015.

[5]江岳文，陈冲，温步瀛.基于随机模拟粒子群算法的含风电场电力系统经济调度[J].电工电能新技术，2007，26(3):37-41.

[6]刘宝碇，赵瑞清.随机规划与模糊规划[M].北京：清华大学出版社，1998:75-77.

[7]刘延风．置换流水车间调度问题的几种智能算法[D].西安:西安电子大学,2012.

[8]蒋镇军.海水淡化优化运行与调度系统的研究与开发[D].杭州:杭州电子科技大学,2012.

Optimal Scheduling of Seawater Desalination Based on Chance Constrained Programming

LIANG Lida, WANG Jian, SUN Guigen

(SchoolofAutomation,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

In order to deal with the uncertainties in the optimal operation problem of seawater desalination system, stochastic simulation technology is used to establish the system dynamic scheduling model based on chance constrained programming, and the economic objective function and constraint conditions are given. The particle swarm optimization algorithm is used to solve the optimization problem. By comparing with redundancy algorithm, it shows that chance constrained programming algorithm has obvious advantages in precision, but its solving speed is slower than redundancy algorithm.

sea water desalination; uncertainty; optimization scheduling; chance constrained programming; particle swarm optimization; stochastic simulation

10.13954/j.cnki.hdu.2016.06.009

2016-05-17

国家自然科学基金资助项目(61374142)；浙江省自然科学基金资助项目(LY16F030006)

梁立达(1990-)，男，浙江台州人，硕士研究生，控制科学与工程.通信作者：王剑副教授，E-mail: wj@hdu.edu.cn.

TP202.7

A

1001-9146(2016)06-0040-05