掌“数”舵 扬“形”帆 让思维启航

福建省松溪县实验小学　潘　丽

掌“数”舵扬“形”帆让思维启航

福建省松溪县实验小学潘丽

数形结合思想是一种重要的数学思想。在教学中渗透数形结合的思想，可去伪存真、化繁为简、化解学习难点。在解决问题的过程中，可提高学生的思维能力和数学素养。适时的渗透数形结合的思想，可达到事半功倍的效果。

小学数学数形结合渗透

“数”与“形”是贯穿整个小学数学教材的两条主线，是贯穿小学数学教学始终的基本内容。我们在研究抽象的“数”的时候，往往要借助直观的“形”，在探究“形”的性质时，又往往离不开“数”。利用数形结合能使“数”和“形”统一起来，以形助数、以数辅形，让数与形各展其长，相辅相成，使许多数学问题变得简易化。本文将结合课堂教学实例谈谈如何在教学中有效渗透数形结合的思想。

一、数形结合——去伪存真，把握概念本质

对于抽象的概念，小学生基本上处于感性直观的认识阶段。数形结合能使比较抽象的概念转化为清晰、具体的事物，让学生经历“将丰富的感性材料加以去粗取精、去伪存真、由表及里”的改造过程，从而让学生更好地发现概念的本质属性。

请看泉州师院附小谢玉娓老师《倍的认识》教学片段：

师：慢羊羊村长用实心小棒摆了一个正方形。数一数用了几根小棒？（4根）

师：如果用空心小棒也摆这样一个正方形，需要几根？（4根）

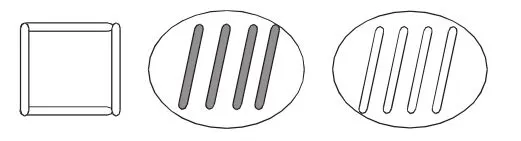
师：也就是要用上1个4。如果我们把4根实心小棒看作一份，空心小棒也是这样的一份，每一份都是4根。瞧，美羊羊又摆了一份空心小棒。

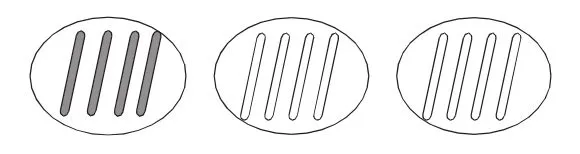
师：请同学们也像这样摆一摆。先在第一行摆出1个4，再在第二行摆出这样的两份。

生动手操作。师巡视指导学生摆小棒。

师：同学们的动手能力真强。你们看，把实心小棒看作一份，空心小棒有这样的几份？

生：2份。

师：每一份都是几根？

生：4根。

师：这样的2份也可以说是几个几？

生：2个4。

师：喜羊羊想在这接着摆一份小棒，请同学们快速地摆一摆，看谁摆得又对又快。

引导说：把实心小棒看作一份，空心小棒有这样的3份，就是3个4。我们就说，空心小棒的根数是实心小棒的3倍。（板书）

师：大家都知道喜羊羊的性子可急了，只见它收走了一份。现在同学们还能不能用到刚认识的“倍”来说一说。

生：空心小棒的根数是实心小棒的2倍。

师：喜羊羊再收走了一份。你们还能说一说吗？

生：空心小棒的根数是实心小棒的1倍。

师：同学们再想想，如果依然把实心小棒看作一份，空心小棒有这样的9份，我们可以说？空心小棒的根数是实心小棒的9倍。

总结：通过刚才的摆小棒我们发现，如果把实心小棒的根数看做一份，空心小棒有这样的几份，我们就说空心小棒的根数是实心小棒的几倍。

从“根数”到“份数”，再到“倍数”，通过摆一摆、圈一圈、说一说，凸显了“倍”的概念本质，帮助学生初步理解了“倍”的概念。这样在教学中运用“数形结合”，把抽象的数学概念直观化，让学生经历知识的形成过程，触及到概念的本质。

二、数形结合——化繁为简，理解数量关系

小学生的思维处于具体形象思维阶段，但许多问题解决的数量关系通常需要抽象思维来理解。因此，这就需要教师通过“数形结合”，用形象化的图形表达抽象化的数量关系，为学生在实际问题与算式之间、在分析数量关系与解决问题之间架设一座“桥”。

如：一袋糖平均分给三个人，如果每人吃掉6粒，那么三人剩下的糖数之和恰好是这袋糖的原来这袋糖有多少粒？用线段图表示数量关系：

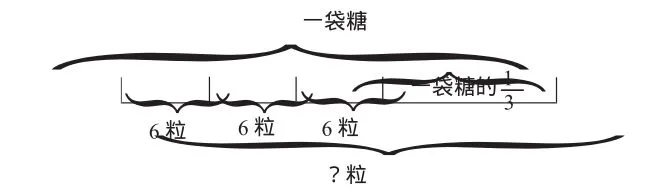
从以上解题过程可以看出，线段图可以帮助学生理解数量关系。对于某些题，如果线段图不能清晰地显示其数量关系，则可以设计出其他图形，使解题过程变得简捷。

如：小明家买了一桶纯净水，连桶共重15千克，喝了一半水后，连桶重8千克。喝掉了多少千克水？原来满桶的水重多少千克？

分析：桶和水之间到底是一种什么样的数量关系？喝了一半水后，桶和水之间又是一种什么样的数量关系？学生对此类数量关系一般感到十分抽象，不容易理解。如果教师运用下面图形来表示，学生就会一目了然。

空桶水

没喝前：○+■＝15千克

喝一半后：○+＝8千克

从图中可知，喝掉的一半水后，轻了7千克，也就是说一半水是7千克，原来满桶的水是7×2＝14（千克）。

可见，渗透数形结合思想，巧妙运用恰当的图形来表示应用题中的数量关系，会使繁杂的数量关系简单化，变“看不见”为“看得见”，能很好地帮助学生理清数量间的关系，提高学生分析问题、解决问题的能力，起到事半功倍的效果。

三、数形结合——从难到易，化解学习难点

学生不能化解难点主要是因为不能实现抽象的内容具体化、形象化、直观化，数形结合能够化抽象为具体、化复杂为简单、变生疏为熟悉、变深奥为浅显。

例如，在学习“异分母分数加减法”时，有些学生不理解为什么要先通分才能相加减，这时，我们可以利用“直观模型”帮助学生理解。

环节一：

师：淘气和笑笑分饼干，（借助多媒体课件动态演示）蓝色部分表示淘气分到的，红色部分表示笑笑分到的，他们都知道自己分到了这块饼干的多少，但不知道他们两个一共分到这块饼干的多少？请大家帮他们想想办法好吗？

师：算式列对了，到底一共分到这块饼干的多少呢？咱们赶紧想想办法吧。

师：怎样化成分母相同的分数呢？

生：通分。

（课件演示）如果我们把这块饼干平均分成了4份，我们就能清楚地看到淘气分了，笑笑分到了，所以他们一共分了

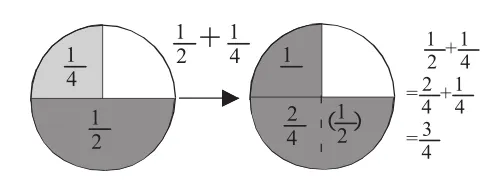
师：大家会利用通分的方法算一算吗？学生列式计算，指名汇报交流。

环节二：

环节三：

师：仔细观察这三题，想一想，发现了什么？（教师边播放课件边讲解）

学生通过观看动态的课件演示，从

“形”的角度体会三道题的共性。课件出示：

讨论二：为什么要把异分母分数转化成同分母分数？（这些算式中都有一个加数是，另一个加数各不相同，转化后的结果也不相同，学生在“变”与“不变”的对比中，发现异分母分数加法的共性。）

上述的教学过程把抽象的分数与形象的图形有机结合起来，学生体会到只有平均分得到的份数相同，也就是分数单位相同，分子才能相加减的道理。学生直观地理解“通分”的必要性及异分母分数加减法的算理，同时抽象能力和抽象水平不断提高，促进思维的发展，轻松地化解了教学难点。

总之，在小学数学教学中，数形结合的思想渗透在数学教学的每一个领域，如果说数学是知识海洋中的一艘船，那么数就是舵，形就是船上的帆，掌好“数”的舵，扬起“形”的帆，数形结合开启思维的航船，才能驶向知识的海洋。