质量偏心影响下的碰摩转子非线性分析
2016-12-13刘桂珍马晓君丁海娟闻邦椿
刘桂珍,于 影,马晓君,丁海娟,闻邦椿
(1.佳木斯大学机械工程学院,黑龙江 佳木斯154007;2.东北大学机械工程与自动化学院,辽宁 沈阳110819)
质量偏心影响下的碰摩转子非线性分析
刘桂珍1,于 影1,马晓君1,丁海娟1,闻邦椿2
(1.佳木斯大学机械工程学院,黑龙江 佳木斯154007;2.东北大学机械工程与自动化学院,辽宁 沈阳110819)
利用拉格朗日方程建立了非稳态油膜力作用下的转子-定子-轴承系统碰摩故障的力学模型,应用数值分析方法研究了该系统随质量偏心变化时的时域波形、轴心轨迹和Poincare截面,揭示了系统分岔特性和进入混沌的途径.研究结果表明:当质量偏心作为唯一控制参数时,系统呈现出复杂的非线性动力学行为.该结果为大型旋转机械的故障诊断提供了理论依据.
碰摩; 时域波形; 轴心轨迹; 庞莱截面
LIU Gui-zhen1,YU Ying1,MA Xiao-jun1,DING Hai-juan1,WEN Bang-chun2
(1.College of Mechanical Engineering,Jiamusi University,Jiamusi 154007,China;2.School of Mechanical Engineering & Automation,Northeastern University,Shenyang 110819,China)
大型旋转机械发生故障时,其振动信号蕴含着丰富的故障信息,通过监测振动信号,实现对转子系统的故障诊断,是目前大型机械或高速旋转系统故障诊断的主要依据.碰摩是旋转机械中最常见的故障之一,也是引起机械系统失效的主要原因之一[1].由于转子系统中存在着诸多的非线性因素,以及加工、装配等原因导致的转子偏心,加剧了转子系统的振动和碰摩现象的产生.因此,转子偏心量是关系到转子动平衡状况及运行稳定性的一个重要参数,对于具有碰摩故障的转子系统,偏心量对系统响应更为重要[2].
本文以转子-定子-轴承系统作为研究对象,利用拉格朗日方程建立了非稳态油膜力作用下的转子系统碰摩故障的力学模型,应用数值分析研究在激励频率不变的情况下,以系统存在质量不平衡作为唯一控制参数时系统的动态响应.通过转子的时域波形图、轴心轨迹和Poincare截面图等振动信号提供的故障信息,对该系统响应的非线性行为和故障机理进行分析,从而为该类转子系统的故障诊断和系统的安全运行提供理论依据.研究结果表明:将转子-定子-轴承系统作为研究对象的4质量8自由度的力学模型比单纯割裂转子系统为“转盘+转轴”的2质量4自由度模型,更接近于生产实际,理论价值尤为彰显[3-7].
1 力学模型与运动微分方程
1.1 拉格朗日方程描述
设有n个质点组成的质点系,受完整的理想约束,具有N个自由度,其位置可由N个广义坐标方程来确定.则有
(1)
式中:L为拉格朗日函数,L=T-V,T为系统的动能函数,V为系统的势能函数;R为与系统阻尼相对应的耗散函数;Qi为作用在系统上的广义力;qi为系统独立的广义坐标;N为系统的总自由度个数.
1.2 运动微分方程
图1为转子-定子-轴承系统碰摩故障的力学模型,转子两端由2个相同的滑动轴承支承,考虑转子与定子的碰摩故障,其力学模型可简化如图1a,b所示.O1为转子的几何中心;Oc为转子质心;kr为定子径向碰摩刚度系数,k1,k2,k3分别为转轴、轴承支撑处和定子基础的刚度系数;c1,c2,c3分别为转轴、轴承支撑处和基础对定子的阻尼系数;e为转子的偏心量;Px,Py分别为转子在水平和垂直方向上碰摩力的分量;Fx,Fy为油膜力的分量;ω为转子角速度;PN为法向碰摩力;PT为切向碰摩力;φ为碰摩点的向径与x轴的夹角;e为转子的偏心量;mi(i=1,2,3,4)分别为转子、轴承、定子和转轴在轴承处的半集中质量;δ为静止时转子与定子之间的初始间隙.

图1 非稳态油膜力的转子-定子-轴承系统碰摩故障的力学模型
假设圆盘不出现回转效应且自转角速度为常数,忽略重力和陀螺力矩的影响,根据非保守拉格朗日方程,推导出量纲为一的非稳态油膜力的转子-定子-轴承系统碰摩故障的动力学方程[4]:
(2)
式中:b为量纲一轴颈的偏心量;ξi(i=1,2,3,4) 分别为转子、轴承、定子和转轴的阻尼比;ηi(i=1,2,3,4) 分别为转子、轴承、定子和转轴的刚度比;ξ23,ξ14分别为轴承相对定子、转子相对于转轴的阻尼比;η23,η14分别为轴承相对定子、转子相对于转轴的刚度比;ρ为量纲一转子的偏心量;xi(i=1,2,3,4)分别为转子中心、轴承中心、定子中心和转轴中心相对于初始位置的量纲一的横向位移;yi(i=1,2,3,4) 分别为转子中心、轴承中心、定子中心和转轴中心相对于初始位置的量纲一的纵向位移;fx,fy为量纲一油膜力;τ=ωt;g为重力加速度;δ2为轴承的平均间隙;σ为Sommerfeld数.
(3)
式中:R为轴承半径;L为轴承宽度.
1.3 非稳态油膜力模型
非线性油膜力模型采用短轴承假设下的Ca-pone非线性油膜力模型[3],该模型有较好的精度和收敛性.在短轴承油膜力假设条件下的无量纲化雷诺方程为:

(4)

由式(4)可得无量纲油膜压力为
(4z2-1)
(5)
式中:D为轴承的直径.
量纲一非线性油膜力最终可以表示为

(6)
式中:

1.4 碰摩力的表达式
为研究方便,不考虑摩擦的热效应,并假定转子与定子部件的碰撞力为弹性变形,转子局部碰摩力模型如图1a,b所示.
由定子径向刚度为kr,转子与定子间的摩擦符合库仑摩擦定律,即摩擦力与作用于接触面上的正压力成正比,设摩擦系数为f,则碰撞力和摩擦力分别为
PN=(e-δ)kr
PT=fPN(e≥δ)
(7)

Px=-PNcosφ+PTsinφ
Py=-PNsinφ-PTcosφ
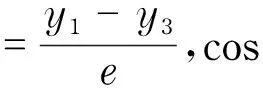
Px=Py=0,(e≥δ)
(8)
2 数值模拟
运用四阶Runge-Kutta法对数值进行求解.在计算中为了能够较快的得到稳定解,应将步长选得尽量小且周期足够多.为了消除瞬态响应的影响,舍弃前40个周期,计算轨迹图时取后10~20个周期.选取系统参数如下:m1=4.0 kg,m2=32.1 kg,m3=50.0 kg,m4=20.0 kg;c1=1.05 kN·s·m-1,c2=2.1 kN·s·m-1,c3=2.1 kN·s·m-1;k1=250 kN·m-1,k2=250 kN·m-1,k3=2 5000 kN· m-1,kr=1 000 kN ·m-1;R=0.025 m,L=0.570 m,δ2=0.2 mm;η=0.018 MPa;R1=0.015 m;f=0.2;通过计算得出转子系统的三级固有频率分别为f1=13.9747 Hz,f2=43.586 4 Hz,f3=113.109 6 Hz,观察图2—8,得出转子系统在激励频度不变的情况下随转子不平衡量变化的振动响应.

图2 ω=380 rad·s-1,偏心量ρ=0.3时转子的系统响应
Fig.2 Response of the rotor system when ω=380 rad·s-1,ρ=0.3

图3 ω=380 rad·s-1,偏心量ρ=0.4时转子的系统响应

图4 ω=380 rad·s-1,偏心量ρ=0.5时转子的系统响应

图5 ω=380 rad·s-1,偏心量ρ=0.7时转子的系统响应

图6 ω=800 rad·s-1,偏心量ρ=0.2时转子的系统响应
为了详细分析转子系统的运动状态,分别做出转动角速度ω=380 rad·s-1,ω=800 rad·s-1时,同一激励频率对应不同偏心量时的时时域波形图、轴心轨迹及Poincare映射,如图2—8所示.
当转动角速度ω=380 rad·s-1时,观察图2—5,得出以下结论:
当偏心量ρ<0.4时,转子时域波形图表现出具有丰富的组合频率,随着偏心量的增大,转子的轴心轨迹范围不变扩大,转子相图表明此时系统处于单点局部碰摩状态,对应的Poincare映射表现为一个独立点,证明系统此时处于周期运动,转子做单周期运动.

图7 ω=800 rad·s-1,偏心量ρ=0.3时转子的系统响应

图8 ω=800 rad·s-1,偏心量ρ=0.4时转子的系统响应
当偏心量ρ=0.4时,转子时域波形图表现紊乱,转子相图和轴心轨迹均处混沌状态,此时的Poincare映射表现为分布在一定区域内不规则的散点图形,证明系统此时已处于混沌状态,转子系统做混沌运动.
当偏心量ρ0.4时,转子时域波形图表现出半频成分振幅激增超过基频振幅,表现出“削波”特征.随着偏心量的增大,转子的轴心轨迹范围不变扩大,转子相图表明此时系统处于多点局部碰摩状态,对应的Poincare映射表现为一个独立点,证明系统此时转子系统处于周期运动,如图2—5所示.
图6—8所示为转动角速度ω=800 rad·s-1时,不同偏心量的Poincare映射、轴心轨迹及时间历程图.
观察图6—8,可以看出ω=800 rad·s-1时,偏心量的存在导致系统由周期运动进入拟周期运动.
3 结 论
(1) 转子系统的不平衡量是导致系统产生混沌的原因之一.当转子转速较低时,偏心量在敏感区域内能产生混沌运动;当转子转速较高时,偏心量的存在是导致系统产生混沌状态的主要原因.因此在工程实际应用中,转速较低时,应尽量避开偏心量的敏感参数区域;转速高时严格控制偏心量,以保证转子系统的稳定运行.
(2) 碰摩和转子不平衡是产生混沌的主要原因,当转子不平衡质量发生变化时,系统以拟周期的失稳方式通向混沌.
(3) 碰摩力可以使转子产生反向涡动,并使系统产生混沌运动,因此在旋转机械中合理选择转、定子之间的间隙尤为重要,可避免因混沌现象导致系统失稳或过早产生疲劳破坏.
(4) 从图2—8可以清楚的看到,转子系统的不平衡量增大时,由于碰摩导致的油膜反向涡动使轴心轨迹发生明显的改变.
[1] 闻邦椿,顾家柳,夏松波,王正等.高等转子动力学[M].北京:机械工业出版社,2000.
WEN Bangchun,GU Jialiu,XIA Songbo,et al.The higher rotor dynamics[M].Beijing:China Machine Press,2000.
[2] 袁惠群.转子系统的若干非线性动力学问题及分岔与混沌研究[D].沈阳:东北大学,2000.
YUAN Huiqun.Some nonlinear dynamic problems of rotor system and the bifurcation and chaos research [D].Shenyang:Northeastern University,2000.
[3] 刘桂珍,于影,李宪芝,等.转子系统非稳态油膜力的非线性分析[J].机床与液压,2013,41(11): 31-34.LIU Guizhen,YU Ying,LI Xianzhi,et al.The nonlinear analysis of unsteady oil film force in rotor system [J].Machine Tool & Hydraulics,2013,41(11):31-34.
[4] 刘桂珍,于影,于峰,等.非稳态油膜力下非线性刚度转子系统的碰摩故障分析[J].中国机械工程.2013,11 (5):432-436.
LIU Guizhen,YU Ying,YU Feng,et al.Rubbing fault study on unsteady oil-film forces for rotor-stator-bearing system[J].Journal of China construction machinery,2013,11 (5):432-436.
[5] 李朝峰,李小彭,马辉,等.非线性连续转子轴承系统碰摩故障动力学行为研究[J].振动工程学报,2009,22 (4):395-399.
LI Chaofeng,LI Xiaopeng,MA Hui,et al.Nonlinear continuous rubbing fault of rotor bearing system dynamics behavior research[J].Journal of Vibration Engineering,2009,22 (4):395-399.
[6] EHRICH F F.Some observations of chaotic vibration phenomena in high speed rotordynamics [J].Transactions ASME Journal of Vibration and Acoustics,1991,113:51-60.
[7] ADILETTA G,GUXLO A R,ROSSI C.Chaos tic motions of a rigid rotor in short journal bearings[J].Nonlinear Dynamics,1996,10( 3):251-269.
Nonlinearanalysis on rub impact rotor with mass eccentricity
With the Lagrange equation,a rub-impact fault mechanical model for rotor-stator-bearing system is first established.By employing the numerical analysis for the time-domain waveform,axis track and Poincare section with mass eccentricity,the system bifurcation characteristic and chaotic route are then revealed.Finally,it is indicated from results that,when the mass eccentricity is treated as the single control parameter,the complex nonlinear dynamical behavior occurs.Therefore,this approach provides the theoretical reference to large rotary machinery fault diagnosis.
rub impact; time-domain waveform; axis track; poincare section
黑龙江省自然科学基金(E201339);佳木斯大学自然科学基金(L2013-067)
刘桂珍(1965-) ,女,工学博士.E-mail:jmslgz@163.com
TH 133
A
1672-5581(2016)01-0021-05
