基于局部均值分解与拉普拉斯特征映射的滚动轴承故障诊断方法

徐倩倩 刘 凯 侯和平 徐卓飞

西安理工大学，西安，710048



基于局部均值分解与拉普拉斯特征映射的滚动轴承故障诊断方法

徐倩倩 刘 凯 侯和平 徐卓飞

西安理工大学，西安，710048

针对滚动轴承非平稳振动信号的特征提取及维数优化问题，提出了融合局部均值分解与拉普拉斯特征映射的轴承故障诊断方法。首先，通过局部均值分解对非平稳振动信号进行平稳化分解，提取乘积函数分量、瞬时频率及瞬时幅值的高维信号特征集；然后，将高维特征集作为拉普拉斯特征映射算法的学习对象，提取轴承高维故障特征集的内在流形分布，以获得敏感、稳定的轴承振动特征参数，实现基于非平稳振动信号分析的滚动轴承故障特征提取；最后，结合支持向量分类模型量化LMD-LE方法的特征提取效果，实现不同状况下的轴承故障分类。轴承故障样本分类识别平均正确率达到91.17%，表明LMD-LE方法有效实现了高维局部均值分解特征集合的降噪，所提取的特征矩阵对轴承故障特征描述准确。

非平稳信号；局部均值分解；拉普拉斯特征映射；故障诊断

0 引言

滚动轴承是旋转机械中最常用也是最易损坏的零部件。据统计，旋转机械中30%的故障是由轴承缺陷引起的。因此，对滚动轴承进行工况监测和故障诊断是非常必要的。然而在工程实际应用中，轴承的运行状态是动态变化的，尤其在设备故障突发期间，机械系统的驱动力、阻尼力及弹性力等动力学参数呈现非线性变化，往往会导致所观测的振动信号表现出较强的非平稳特性。

局部均值分解 (local mean decomposition, LMD) 方法是一种自适应时频分析方法，通过自适应的信号分解和降噪能力兼顾了信号在时域和频域的局部化特征和全貌。相比线性时频分析、双线性时频分析及参数化时频分析方法[1]，LMD可解决固定类型基函数可能会产生虚假的时频信息问题、多参数优化导致计算量大问题及Heisenberg原理在时频域的限制性问题, 在轴承故障信号处理中应用广泛。文献[2-7]应用LMD处理轴承振动信号，取得了较好的应用效果；文献[8-11]分别将LMD与非局部均值去噪、双树复小波降噪、奇异值差分谱、改进形态滤波法结合，实现了振动信号及分量的降噪处理；文献[12-15]分别利用马氏距离、灰色相似关联度、变量预测模型、隐马尔可夫模型等故障分类方法实现了基于LMD的轴承故障分类。

然而，在信号分量中提取的丰富信号特征集往往存在着大量冗余信息和相关信息，反而会彼此干扰并产生模式混淆，在很大程度上影响故障模式识别的效果。因此，有必要对冗余信号特征集进行维数优化处理以实现数据降噪。但现有基于LMD的轴承故障诊断方法并未对高维特征矩阵进行优化处理，故本文进一步提出了融合LMD与拉普拉斯特征映射(Laplacian eigenmap,LE)算法的轴承故障诊断方法，将局部均值分解的特征集合作为LE算法的高维特征输入，完成高维特征集的准确提取，最终实现不同故障程度、不同故障类型的轴承故障分类。

1 基于LMD的非平稳信号分解

近年来，众多学者提出了一些结合复杂信号自身特点的自适应分解时频分析方法，其中应用最为广泛的是经验模态分解(empirical model decomposition, EMD)。LMD是由EMD方法原理发展而来的，可以有效解决EMD有可能产生的物理意义无法解释的瞬时频率问题，避免EMD的过包络和欠包络问题，成为现有自适应时频分析方法的研究热点。对于任意检测信号x(t)，其LMD算法步骤如下。

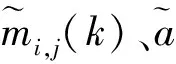
(1)

(2)

(3)

(4)

然后，分别计算瞬时幅值ai(t)、瞬时频率fi(t)及信号分量PFi(t)，并获得新的信号ui(t)=x(t)-PFi(t)，若ui(t)不是单调函数，则将ui(t)作为新的信号重复上述步骤，直至ui(t)满足单调函数条件。即

(5)

PFi(t)=ai(tj)si,j(t)

(6)

fi(t)=d(arccos(si,j(t)))/(2πdt)

(7)

最终，LMD通过三重循环将x(t)分解为一系列PFi(t)分量与余项ui(t)的和，将非平稳信号的特征提取问题转换为平稳分量的特征提取问题。即

x(t)=∑PFi(t)+ui(t)

(8)

2 基于LE的故障特征集维数优化

现有的高维数据降维方法可分为线性降维方法、基于核函数的非线性降维方法以及基于特征值的非线性降维方法，其代表性方法分别为主元分析(principle component analysis, PCA)法、核主元分析(kernel principle component analysis, KPCA)法及LE算法。研究表明LE算法适用于设备工况特征的高维数据的非线性特征挖掘和降维，并取得了良好的去冗余效果[16-19]。

根据图谱理论，如果数据均匀采样自高维空间中的低维流形，流形上的拉式算子可以由图上的Laplacian逼近，而图上最前面的几个特征向量就是流形上 L-B算子特征函数的离散逼近，最终实现高维流形的最优嵌入。若第i个节点xi和第j个节点xj之间有边连接，由热核法确定边的权值为

Wij=exp(-‖xi-xj‖2/σ2)

(9)

构建拉普拉斯特征矩阵L=D-W,假设构建的近对邻图是连通的，那么寻找低维嵌入的问题就归结为对广义特征向量问题的求解：

Ly=λDy

(10)

可见，LE算法通过对矩阵特征值和特征向量的求解实现了特征集的降维和特征提取，不需要进行迭代运算，减小了计算量，缩短了算法运行时间。为有效实现高维轴承故障特征集的维数优化，获得故障特征的精确描述，本文采用LE算法进行轴承故障冗余特征集处理，通过对高维非线性数据进行降维，从高维非线性数据中找出隐藏在高维观测空间数据中的低维结构表示，揭示数据的内在流形分布。

3 LMD与LE融合算法

如图1所示，基于LMD和LE的轴承故障诊断方法步骤如下：

(1)根据LMD算法对多样本轴承故障信号x(t)进行LMD分解。获得信号分量曲线PFi、瞬时幅值曲线a及瞬时频率曲线f。依据峭度最大原则选择PF1作为故障特征频带[22]，分别提取PF1曲线的波形指标、裕度指标、峭度指标、脉冲指标、峰值指标共5个时域特征及PF1、a1、f1曲线的均方根值、绝对平均值、方根幅值、峭度、偏斜度、峰-峰值共6个线型特征，构成23维故障特征集X。

(2)根据LE算法对特征集X进行维数优化。将23维故障特征集作为LE算法的高维特征输入，选用K近邻域(KNN)法构建近邻图G，计算高维矩阵X映射到低维空间的权重矩阵W及拉普拉斯特征矩阵L的特征向量构成的低维坐标矩阵T。

(3)通过SVM分类模型完成轴承故障样本的分类识别。将特征映射矩阵T作为轴承故障样本特征参数，由多类故障数据集构成SVM模型的训练样本及测试样本，通过模型参数的交叉验证寻优完善SVM模型，实现多类轴承故障的分类识别。

图1 基于LMD和LE的轴承故障诊断方法

4 SKF6205-2RS轴承故障实验

SKF6205-2RS型滚动轴承实验中采用的数据均来自美国凯斯西储大学电气实验室的轴承故障数据库。电机负载约1470 W,转速为1750 r/min，采样频率为12 kHz，其传感器位置为驱动端的轴承座上垂直位置。损伤程度a、b、c分别代表0.178 mm、0.356 mm、0.533 mm，轴承故障A、B、C、D分别代表正常状态及不同损伤程度下故障、滚动体故障、内圈故障、外圈故障，建立故障数据库：

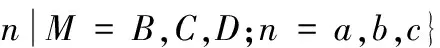
其中，M.n表示n损伤程度下的M类故障数据，具体故障样本分组见表1。

表1 实验数据分组

在本实验中，以轴承转一圈所采集的数据点数的两倍作为确定样本长度的参考[23]，则轴承正常及各种故障状态下的数据采样长度N=1000，样本数为100。图2～图4所示分别为轴承滚动体故障、内圈故障及外圈故障数据经LMD获得的PF1、a1、f1曲线。提取轴承每组故障信号的100个样本构成100×23维故障数据集，作为降维算法的高维特征集输入。

图2 PF1、a1、f1 曲线(滚动体故障)

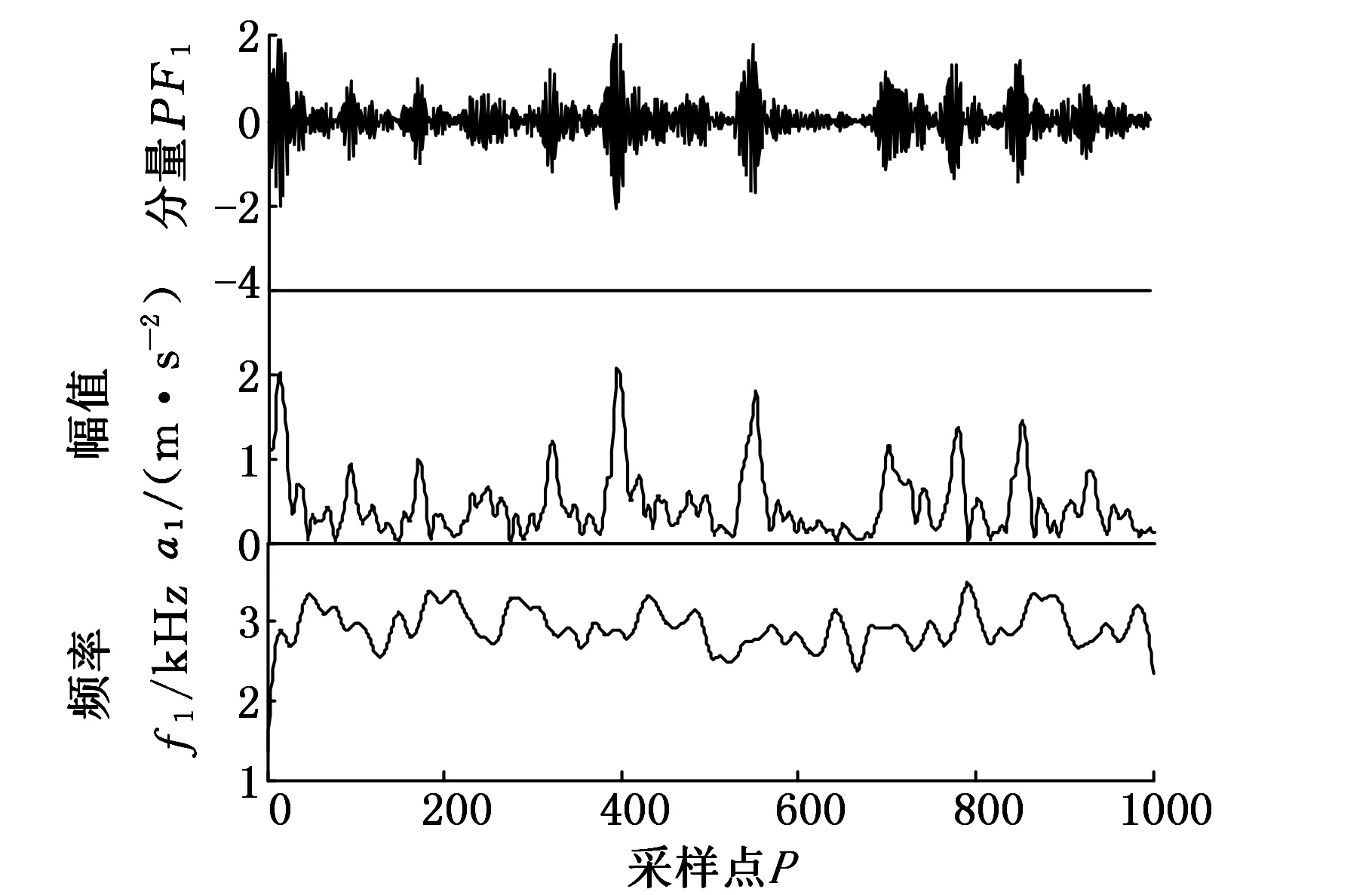
图3 PF1、a1、f1 曲线(内圈故障)

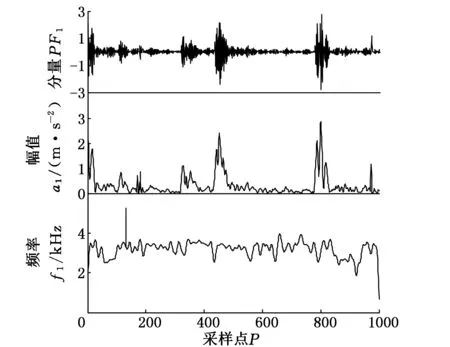
图4 PF1、a1、f1 曲线(外圈故障)

分别采用PCA、KPCA及LE算法对轴承状态特征矩阵进行维数优化处理，选取优化目标维数为3。图5～图10所示分别为故障集1～故障集6的LMD特征降维效果。

(a)PCA (b)KPCA (c)LE图5 三种降维方法对LMD特征聚类效果(故障集1)

(a)PCA (b)KPCA (c)LE图6 三种降维方法对LMD特征聚类效果(故障集2)

(a)PCA (b)KPCA (c)LE图7 三种降维方法对LMD特征聚类效果(故障集3)

(a)PCA (b)KPCA (c)LE图8 三种降维方法对LMD特征聚类效果(故障集4)

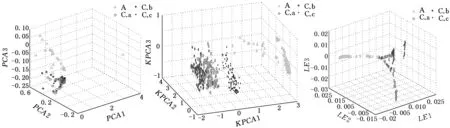
(a)PCA (b)KPCA (c)LE图9 三种降维方法对LMD特征聚类效果(故障集5)

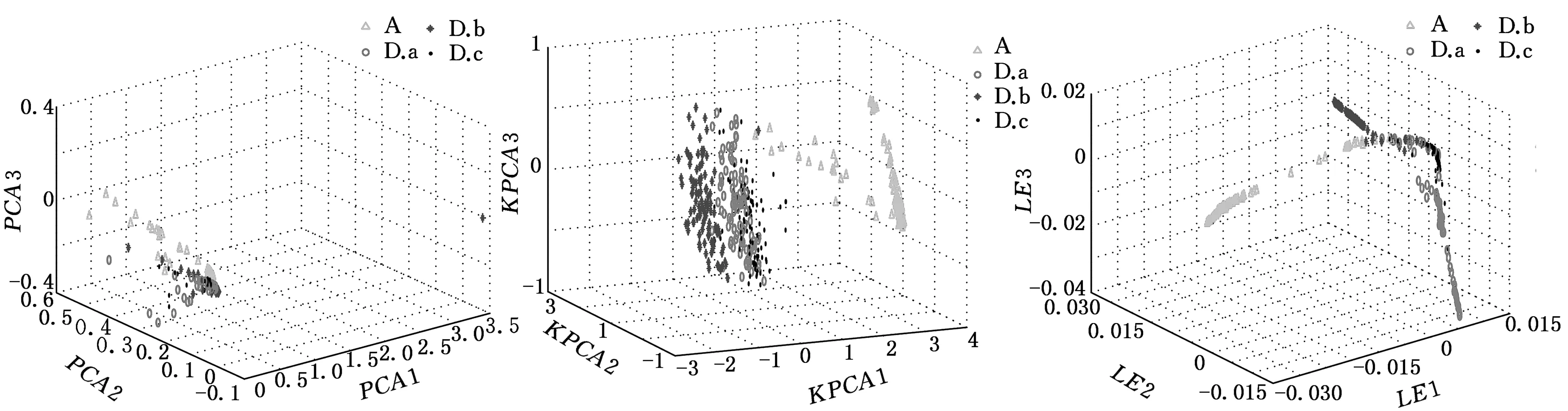
(a)PCA (b)KPCA (c)LE图10 三种降维方法对LMD特征聚类效果(故障集6)

由图5～图10对比发现，三种方法都成功分离出正常样本数据，但对其余三类样本的聚类效果并不相同：PCA方法处理使得不同工况样本类内距最小，有效实现了同类样本的聚集，但类间距最小，无法区分出不同类别故障样本，样本聚类可视化效果差；KPCA方法相比PCA方法，扩大了类间距，不同类样本的分离效果略有提高，但是不同类别样本重合度高，使得样本聚类效果变差，增加了轴承故障诊断的复杂度；LE方法相比前两种方法，类间距明显增大，样本点虽有重合但样本聚类效果最强，故障特征更具有代表性，有利于轴承故障类型的诊断识别。

可见，基于特征的LE降维方法对不同类型样本的类间距最大，分类识别效果优于线性降维及基于核函数的降维方法。故本文选取LE算法对LMD特征集进行维数优化，去除特征向量间的冗余性，降低轴承故障分类识别的复杂度。

为量化LMD-LE方法的特征提取效果，本文结合支持向量机(SVM)作为故障类型的分类识别工具。取每类故障的前50组样本作为训练矩阵，并对后50组样本作为测试样本进行类型预测，测试样本正确识别率见表2。可见7组故障集的测试样本识别正确率平均达到91.17%：故障集1～故障集3代表同一故障程度下的滚动体、内圈、外圈故障，其测试样本识别正确率达到92%以上，说明本文方法对不同类轴承故障特征提取效果明显；故障集4～故障集6代表不同故障程度下同一类故障，其测试样本识别正确率略低于不同类故障的识别率，测试样本的故障类型与预测结果基本吻合；故障集7属于不同故障程度、不同故障类型下的复杂多类别故障分类问题，在分类正确率上低于前6组故障集。图11为第7组故障集的测试样本类型预测图，错误分类样本均匀分布在多个故障样本中，属于全局性问题，或由信号噪声、算法误差造成，但分类正确率仍达到85%以上，基本实现了复杂故障样本的分类。

表2 SVM测试样本识别正确率

图11 第7组测试样本分类预测结果

5 结论

(1)LE方法在去除故障特征集合的冗余性方面具有明显优势。

(2)LMD与LE的融合应用对滚动轴承故障特征提取效果良好，降低了故障特征集的复杂程度，为非平稳振动信号特征参数提取提供了新的方法。后续研究应结合信号滤波降噪法对振动信号进行预处理，更进一步提高特征提取准确性。

[1] 唐友福.基于广义局部频率的非线性非平稳信号故障特征提取方法研究[J].机械工程学报,2015,51(11):81-81. Tang Youfu. Study on Fault Feature Extraction for Nonlinear Nonstationary Signals Based on General Local Frequency[J]. Journal of Mechanical Engineering, 2015, 51(11): 81-81.

[2] 陈保家,何正嘉,陈雪峰，等.机车故障诊断的局域均值分解解调方法[J].西安交通大学学报,2010,44(5):40-44. Chen Baojia, He Zhengjia, Cheng Xuefeng,et al. Locomotive Fault Diagnosis Based on Local Mean Decomposition Demodulating Approach [J]. Journal of Xi’an Jiaotong University, 2010,44(5):40-44.

[3] 杨宇,王欢欢,程军圣，等.基于LMD的包络谱特征值在滚动轴承故障诊断中的应用[J].航空动力学报,2012,27(5):1153-1158. Yang Yu, Wang Huanhuan, Cheng Junsheng, et al. Application of Envelope Spectrum Characteristics Based on LMD to Roller Bearing Fault Diagnosis[J].Journal of Aerospace Power,2012,27(5):1153-1158.

[4] 侯蒙蒙,许同乐,高朋飞，等.基于LMD分解的风机轴承故障信号提取研究[J].中国农机化学报,2015,36(2):277-279. Hou Mengmeng, Xu Tongle, Gao Pengfei, et al. Methods of Bearing Fault Characteristic Signal Extraction[J]. Journal of Chinese Agricultural Mechanization，2015,36(2):277-279.

[5] 程军圣,杨怡,杨宇，等.基于LMD的能量算子解调机械故障诊断方法[J].振动、测试与诊断,2012,32(6):915-919. Cheng Junsheng, Yang Yi, Yang Yu, et al. Mechanical Fault Diagnosis Method of Energy Operator Demodulating Approach Based on LMD[J].Journal of Vibration Measurement & Diagnosis,2012,32(6):915-919.

[6] 王衍学,何正嘉,訾艳阳，等.基于LMD的时频分析方法及其机械故障诊断应用研究[J].振动与冲击,2012,31(9):9-12. Wang Yanxue,He Zhengjia,Zi Yanyang, et al.Several Key Issues of Local Mean Decomposition Method Used in Mechanical Fault Diagnosis[J]. Journal of Vibration and Shock, 2012,31(9):9-12.

[7] 黄浩,吕勇,肖涵，等.基于PCA和LMD分解的滚动轴承故障特征提取方法[J].仪表技术与传感器,2015(4):76-78. Huang Hao, Lü Yong, Xiao Han, et al.Feature Extraction Method of Rolling Bearing Fault Based on Principal Component Analysis and Local Mean Decomposition[J]. Instrument Technique and Sensor, 2015(4):76-78.

[8] 祝青林,吕勇,李宁，等.非局部均值去噪和LMD综合的滚动轴承故障诊断[J].机床与液压,2015,43(13):172-176. Zhu Qinglin,Lü Yong, Li Ning, et al.Fault Diagnosis to Rolling Bearing by Integration of Nonlocal Means De-noising and LMD[J]. Machine Tool & Hydraulics, 2015,43(13):172-176.

[9] 侯蒙蒙,许同乐.基于DT-LMD机床轴承故障信号提取研究[J].机床与液压,2015,43(7):185-188. Hou Mengmeng, Xu Tongle. Study of Bearing Fault Signal Extraction of Machine Tool Based on DT-LMD[J]. Machine Tool & Hydraulics,2015,43(7):185-188.

[10] 马朝永,刘茜,段建民，等.基于LMD与奇异值差分谱的滚动轴承故障诊断方法[J].北京工业大学学报,2014,40(2):182-188. Ma Chaoyong, Liu Qian, Duan Jianmin, et al.Fault Diagnosis Method of Rolling Bearings Based on LMD and Singular Value Difference Spectrum[J]. Journal of Beijing University of Technology, 2014,40(2):182-188.

[11] 冯研研,艾延廷,周海仑，等.改进形态滤波与LMD结合的滚动轴承故障诊断方法研究[J].机械设计与制造,2015(1): 83-86. Feng Yanyan, Ai Yanting, Zhou Hailun,et al. Study on Improved Morphological Filter and LMD Fault Diagnosis of Roller Bearing[J]. Machinery Design & Manufacture, 2015(1):83-86.

[12] 葛明涛,董素鸽.LMD及马氏距离敏感阈值的滚动轴承故障诊断[J].机械设计与制造,2015(2):210-213. Ge Mingtao, Dong Suge. Fault Diagnosis Method of Rolling Bearings Based on LMD and Mahalanobis Distance Sensitive Threshold [J]. Machinery Design & Manufacture, 2015(2):210-213.

[13] 程军圣,罗颂荣,杨斌，等.LMD能量矩和变量预测模型模式识别在轴承故障智能诊断中的应用[J].振动工程学报,2013,26(5):751-757. Cheng Junsheng, Luo Songrong, Yang Bin, et al. LMD Energy Moment and Variable Predictive Model Based Class Discriminate and Their Application in Intelligent Fault Diagnosis of Roller Bearing [J]. Journal of Vibration Engineering,2013,26(5):751-757.

[14] 孟宗,闫晓丽,王亚超.基于LMD和HMM的旋转机械故障诊断[J].中国机械工程,2014,25(21):2942-2946. Meng Zong, Yan Xiaoli, Wang Yachao. Rotating Machinery Fault Diagnosis Based on Local Mean Decomposition and Hidden Markov Model[J]. China Mechanical Engineering,2014, 25 (21):2942-2946.

[15] 裴峻峰,于志远,董雪，等.基于LMD和灰色相似关联度的轴承故障诊断方法[J].机械设计与制造,2015(4):66-69. Peng Junfeng, Yu Zhiyuan, Dong Xue, et al. Roller Bearing Fault Diagnosis Method Based on LMD and Grey Similar Incidence[J]. Machinery Design & Manufacture, 2015(4):66-69.

[16] 贾茂林,王孙安,梁霖.利用非线性流形学习的轴承早期故障特征提取方法[J].西安交通大学学报,2010,44(5):45-49. Jia Maolin, Wang Sun’an, Liang Lin. Feature Extraction for Incipient Fault Diagnosis of Rolling Bearings Based on Non-linear Manifold Learning[J]. Journal of Xi’an Jiaotong University,2010,44(5):45-49.

[17] 赵斐,陆宁云,杨毅，等.基于工况识别的注塑过程产品质量预测方法[J].化工学报,2013,64(7):2526-2534. Zhao Fei, Lu Ningyun, Yang Yi, et al. Product Quality Prediction Method for Injection Molding Process Based on Operating Mode Recognition[J]. CIESC Jorunal,2013,64(7):2526-2534.

[18] 刘海涛,汪增福,曹洋，等.基于流形学习的三维步态鲁棒识别方法[J].模式识别与人工智能,2011,24(4):464-472. Liu Haitao, Wang Zengfu, Cao Yang, et al. 3D Robust Gait Recognition Based on Manifold Learning[J]. Pattern Recognition and Artificial Intelligence,2011,24(4):464-472.

[19] 李月仙,韩振南,黄宏臣，等.基于拉普拉斯特征映射的旋转机械故障识别[J].振动与冲击,2014,33(18):21-25. Li Yuexian, Han Zhennan, Huang Hongchen, et al. Fault Diagnosis of Rotating Machineries Based on Laplacian Eigenmaps[J].Journal of Vibration and Shock, 2014,33(18):21-25.

[20] He Qingbo. Vibration Signal Classification by Wavelet Packet Energy Flow Manifold Learning[J].Journal of Sound and Vibration,2013,332(7):1881-1894.

[21] He Qingbo. Time-frequency Manifold for Nonlinear Feature Extraction in Machinery Fault Diagnosis[J]. Mechanical Systems and Signal Processing,2013,35(1/2):200-218.

[22] 李宏坤, 赵长生,周帅，等. 基于小波包-坐标变换的滚动轴承故障特征增强方法[J].机械工程学报, 2011,47(19):74-80. Li Hongkun, Zhao Changsheng, Zhou Shuai, et al. Fault Feature Enhancement Method for Rolling Bearing Based on Wavelet Packet-coordinate Transformation[J].Journal of Mechanical Engineering, 2011,47(19):74-80.

[23] 张媛,秦勇,邢宗义，等.基于LMD-PCA-LSSVM的滚动轴承安全域估计和状态辨识方法[J].振动与冲击,2013,32(20): 172-178. Zhang Yuan, Qin Yong, Xing Zongyi, et al.Safety Region Estimation and State Identification of Rolling Bearings Based on LMD-PCA-LSSVM[J]. Journal of Vibration and Shock, 2013, 32(20):172-178.

(编辑 陈 勇)

Fault Diagnosis Method of Bearings Based on LMD and LE

Xu Qianqian Liu Kai Hou Heping Xu Zhuofei

Xi’an University of Technology, Xi’an, 710048

A new diagnosis method for feature extraction of non-stationary vibration signals and fault classification of rolling bearings was proposed based on LMD and LE. Firstly, the non-stationary vibration signals of rolling bearings were decomposed into several product functions with LMD. Then, dimensional fault feature sets were established by the time-frequency domain features of product function, instantaneous frequency and amplitude. Secondly, LE was introduced to extract the sensitive and stable characteristic parameters to describe the running states of rolling bearings effectively and accurately. Finally, support vector machine classification model was built to realize the classification of fault bearings. For test samples classification, the average prediction accuracy is as 91.17%.It means that the fusion method of the LMD and LE is suitable and feasible for the bearing fault feature extraction.

non-stationary signal; local mean decomposition(LMD); Laplacian eigenmap(LE); fault diagnosis

2015-10-21

国家自然科学基金资助项目(51275406)；国家青年科学基金资助项目(51305340)

TH17

10.3969/j.issn.1004-132X.2016.22.016

徐倩倩，女，1989年生。西安理工大学机械与精密仪器工程学院博士研究生。主要研究方向为机械状态信号处理、故障诊断。刘 凯，男，1957年生。西安理工大学机械与精密仪器工程学院教授、博士。侯和平，男，1978年生。西安理工大学印刷包装与数字媒体学院副教授、博士研究生。徐卓飞，男，1985年生。西安理工大学印刷包装与数字媒体学院讲师、博士。