地铁车辆电动塞拉门的剩余寿命预测

王 凌 陈长骏 潘 静 许 宏 陈锡爱 那文波

中国计量大学，杭州，310018



地铁车辆电动塞拉门的剩余寿命预测

王 凌 陈长骏 潘 静 许 宏 陈锡爱 那文波

中国计量大学，杭州，310018

针对地铁车辆客室电动塞拉门传动装置润滑不良的问题，提出了基于自组织映射(SOM)神经网络、隐马尔可夫链(HMC)模型和蒙特卡罗(MC)仿真的剩余使用寿命预测方法。该方法首先对采集到的电机电流信号进行特征提取；然后利用SOM对提取出的多维特征数据进行融合与编码，将所得结果作为HMC的输入向量，训练得到全部寿命下劣化状态转移矩阵；最后利用MC方法实现对其劣化过程的剩余使用寿命预测。故障模拟实验结果表明，该方法可以在考虑润滑不良故障模式下，有效预测得到电动塞拉门丝杆的剩余使用寿命。

电动塞拉门；润滑不良；剩余使用寿命预测；隐马尔可夫链模型；自组织映射神经网络；蒙特卡罗仿真

0 引言

丝杆作为地铁电动塞拉门的关键传动部件，其运行状态直接关系到机械设备本身的运行安全，同时也会对后续的运行造成直接影响。据统计，润滑不良所造成的机械故障约占整个机械故障的75%[1]，润滑不良同时也是地铁车辆客室电动塞拉门的主要故障之一[2]。因此，对地铁电动塞拉门丝杆润滑不良的故障进行预测具有十分重要的理论研究与工程实用价值。目前，已有一些利用振动信号实现机电设备故障预测的方法，而基于电机电流信号进行机电设备故障预测的研究正逐步成为热点[3]。基于数据驱动的故障预测[4]方法是通过对采集到的相似设备历史数据集进行建模的，因此，设备劣化过程数据的采集是实现基于数据驱动预测的关键。文献[5]利用PCA方法对轴承振动信号中的多种特征参数进行融合，然后输入已构建的极限学习机模型，实验结果表明该方法有较好的预测精度。文献[6]提出了一种融合最小二乘支持向量机和统计过程控制技术的故障预测方法，该方法能够及时地判断风电机组齿轮箱的异常状态。文献[7]构建了SVM与马尔可夫模型，对轴承进行了寿命预测。文献[8]结合粗糙集与灰色理论，利用粗糙集进行特征提取，然后通过灰色模型对设备实现了准确预测。

隐马尔可夫链[9](hidden Markov chain,HMC)模型可以很好地描述内部状态与外部测量结果之间的关系，并能根据观测序列识别出隐含的状态转移矩阵。为了更加全面准确地反映设备地铁车辆客室电动塞拉门丝杆的劣化状态，本文采用自组织映射(self-organizing feature map, SOM)网络对提取的多个电机电流信号进行特征融合，构建了基于自组织映射网络、HMC和蒙特卡罗(Monte Carlo，MC)仿真的剩余使用寿命(remaining useful life, RUL)预测方法，相比文献[5-8]，该方法的优点在于，不仅可以得到设备劣化过程模型，而且可以估计剩余使用寿命。最后，将该方法应用于地铁电动塞拉门丝杆润滑不良实验。

1 基于SOM-HMC-MC的剩余使用寿命预测方法

SOM-HMC-MC剩余使用寿命预测方法由四个步骤组成：①数据处理和特征提取，即首先对采集到的电机电流信号进行滤波，再分别提取均方根、峰峰值、偏度指标、峭度指标和Shannon小波能量熵值特征参数的过程；②利用SOM方法对获取的全寿命多维特征向量进行信息融合并编码的过程；③将编码后的结果作为特征向量输入HMC进行训练并得到状态转移矩阵的过程；④利用Viterbi算法获取观测序列下的状态，再用MC方法在线估计设备RUL的过程。

1.1 电流信号特征提取

采集到的大量原始数据不可避免地存在一些冗余以及与劣化状态不相关的监测数据，这会导致预测过程中计算量增大、精度下降。因此，在原始数据中提取出能有效表征其劣化特征的参数，对于后续预测分析尤为重要。

Shannon能量熵值反映了信号能量概率分布的均匀性[10]，它能提供信号在动态过程中的有用信息，因此，选择容错性强的Shannon能量熵作为时频特征向量。本文选取sym4小波对信号进行3层小波包变换，分解得到8个频段，计算出不同频段能量cj,k(i)，再根据下式：

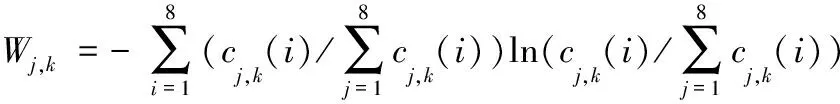
(1)

分别提取出8个频段的能谱熵向量W=(W3，0,W3，1,…,W3，7)。其中，cj,k(i)为第j层节点k上的小波包能量，同时为了得到劣化数据更多的信息，进一步提取均方根、峰峰值、偏度指标、峭度指标作为时域特征向量。

1.2 SOM神经网络信息融合

信息特征融合可将高维特征数据降至较低空间中，并保留原始空间中的一些基本性质。将具有共同特点的样本数据在降维后聚集在一起的同时，也能够将多个特征数据之间的冗余信息予以消除。SOM是实现该方法的理想选择[10]。

SOM是一种无监督、自组织、自学习的神经网络[11]，可以根据自己的学习规律对输入数据之间的相似度进行自组织分类。在网络结构上，它由输入层和映射层构成，映射层之间各神经元为相互连接，且各神经元之间通过相互兴奋、抑制和竞争来获取对输入模式的响应机会。通过训练得到以最优神经元为中心、其相邻区域Nj*(t)内的若干神经元共同来表示输入模式的聚类结果。

本文在进行地铁车辆客室电动塞拉门传动装置剩余使用寿命预测的过程中，首先通过训练好的SOM建立一种分类模型，通过向该模型输入多维特征向量，输出该特征向量的编码实现信息的融合，作为后续HMC模型的输入观测值。

1.3 HMC模型原理

HMC模型是一种状态空间模型，其真实劣化状态是不可见的，通过对观测序列的随机过程来感知某一状态的存在，故该模型的状态转移矩阵表现为隐式随机过程，与其相关联的观测值为显示随机过程。HMC模型不仅可体现各状态之间的相关性，而且考虑到在各状态下的观测序列的独立性，HMC模型一般用5个主要参数表示：

λ=(N,M,A,B,π)

(4)

式中，N为隐状态数；M为每个状态可能对应的观测值个数；A为状态转移矩阵；π为初始状态的概率分布矩阵；B为观测值概率矩阵。

将HMC模型应用到实际工程中，通常采用Forward-Backward算法来解决模型参数估计问题，即在给定的模型结构和观测序列条件下，计算并估计最优的模型参数，能够有效地得出产生观测序列的概率。采用Viterbi算法求解出最优状态序列，即给定观测序列和模型，得到某一时刻的最佳状态。采用Baum-Welch算法通过不断的迭代计算获得HMC模型修正后的参数，即给定初始模型参数和观测序列，得到调整后的参数。

综上所述，在考虑润滑不良故障时，基于SOM-HMC-MC的电动塞拉门丝杆的RUL预测过程如图1所示。其中，“参数初始化”设定如下：当前使用寿命长度Rul=0，仿真循环次数阈值Ns=10 000，已仿真的使用寿命周期数Cyct=1，dmax为故障状态。

本文采用平均绝对百分误差(mean absolute percentage error,MAPE)Emap、累积相对精度(cumulative relative accuracy,CRA)Acr、拟合系数(R-square)Rsqu以及均方根误差(root mean square error,RMSE)Erms对SOM-HMC-MC算法的预测性能进行评估。其中，MAPE、CRA和RMSE越小，拟合系数越高，表明模型预测性能越好。各变量表达式分别为

(5)

(6)

(7)

(8)

2 故障劣化模型

地铁车辆客室塞拉门丝杆的润滑状态从正常到失效需要经历一系列的劣化状态，最终到达故障状态。在不考虑设备维修的情况下，其劣化过程是不可逆的，每个状态有一定概率向自身进行状态转移，同时也可能转移到其右侧更高的状态编号[12]，其拓扑结构如图2所示。

由于机械类故障的渐变几乎都服从指数退化模型[13]，其劣化过程需要数月甚至数年之久，故较难获得其充分的故障劣化数据。本文基于文献[14]提出的人为模拟润滑不良劣化过程的思想，在实验中通过对其负载逐渐的增大来模拟润滑不良劣化过程。

在无先验信息的条件下，不同样本下的劣化过程由下式给出[13]：

(9)

其中，Φ为模型常数；β为正态分布随机变量(均值为μβ，标准差为σβ)；ε(ti)为误差项，服从标准正态分布N(0, σ2)。考虑到本文故障模拟实验条件和特点，其中参数确定为Φ=0.1，μβ=0.9，

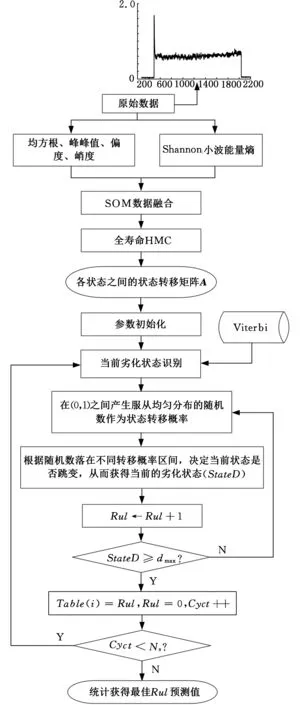
图1 基于SOM-HMC-MC的电动塞拉门丝杆RUL预测流程(考虑润滑不良故障)

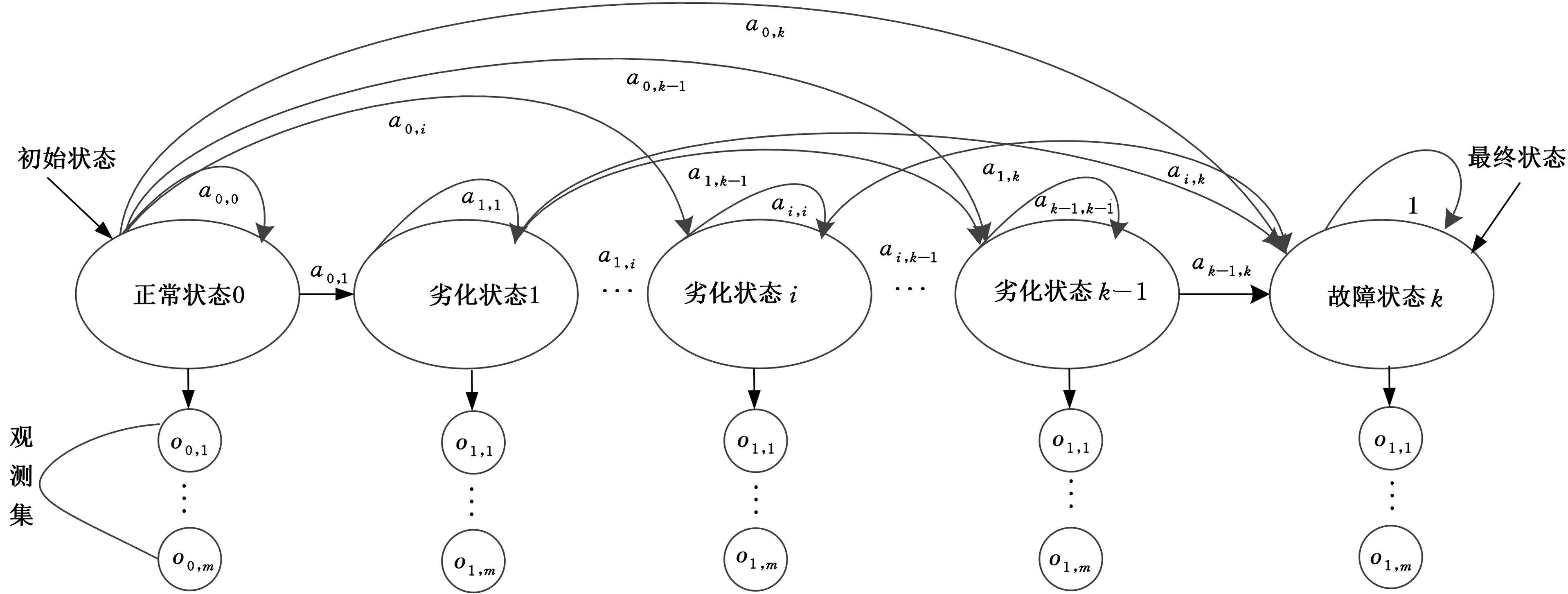
图2 地铁车辆电动塞拉门丝杆的劣化状态变迁过程

σβ=0.15，其结果如图3所示。图3为10组全寿命下的数据样本，其中纵轴表示人为施加的劣化过程(分为10个劣化状态，例如y取值从1.5到2为劣化2)，横轴表示每个劣化过程所持续的时间。后文基于上述样本数据，根据劣化曲线组合成不同全寿命下劣化样本进行预测分析。

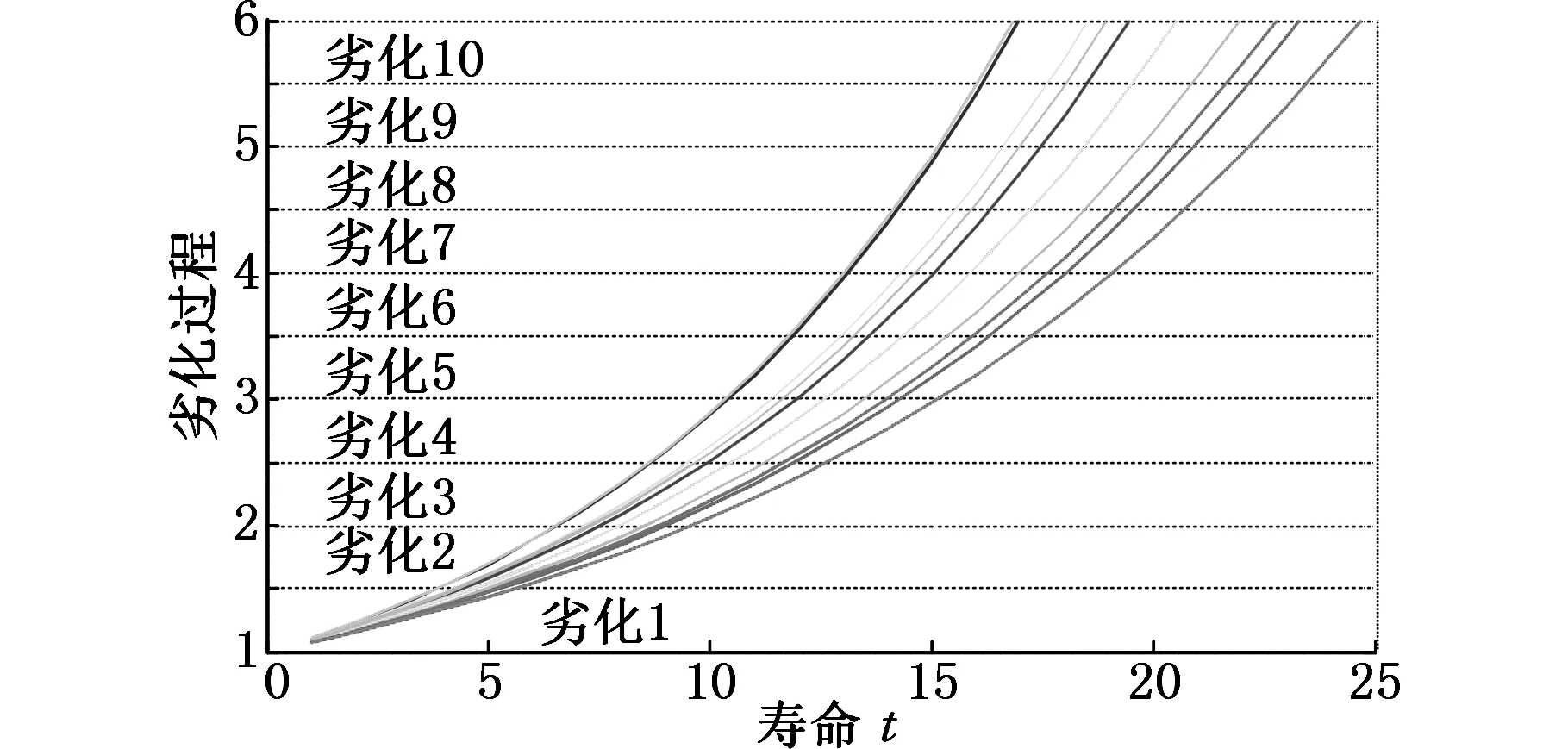
图3 地铁车辆电动塞拉门丝杆的润滑不良故障劣化曲线

3 实验仿真与结果分析

3.1 数据采集

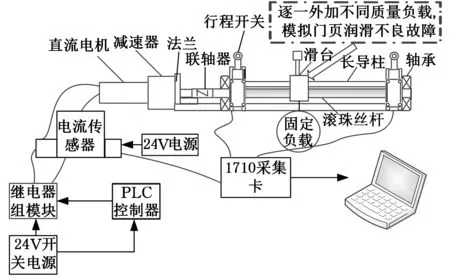
图4 地铁车辆客室电动塞拉门的丝杆润滑不良故障模拟实验装置

本文针对地铁车辆客室电动塞拉门的丝杆润滑不良故障进行故障模拟实验。如图4所示，实验设备包括一台24 V直流电机，与之连接的是减速比为3的减速箱，减速后额定转速为600 r/min，并通过联轴器驱动有效行程为300 mm、导程为10 mm的丝杠来模拟地铁电动塞拉门丝杆润滑不良故障。实验中利用±5V电流传感器采集直流电机工作电流，采用研华PCI1710采集卡与LABVIEW数据采集软件对模拟信号进行连续采集，并传输计算机以文本形式保存。

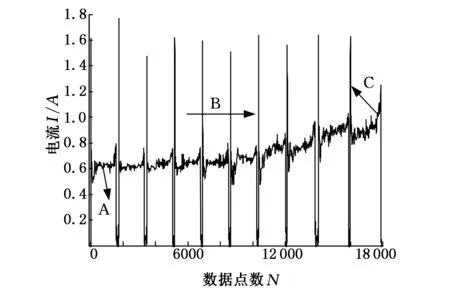
A.润滑良好健康状态 B.润滑不良劣化过程 C.故障状态图5 电动塞拉门丝杆润滑不良故障劣化过程

实验中每隔4.5 s采样保存一组数据，采样频率为512 Hz，故一组数据长度为2300，通过在丝杆垂直方向上施加负载，即在没有施加任何负载工况下(仅有固定负载模拟车门)，视为丝杆运行处于正常，随后逐渐施加不同质量负载模拟为一种劣化情况进行采集。实验中共准备了9块不同质量的铁块，并且将铁块的质量以从小到大施加到设备上，以模拟润滑不良劣化过程的指数趋势。每施加一次负载都代表一个离散劣化过程(并非实际状态)。每施加一次负载都代表一个劣化过程(并非实际状态)，负载全部施加上表示故障状态。在实验中，模拟10种劣化过程，每种劣化情况下均取15组数据，共组成150组实验数据，再根据第2节的劣化曲线从这150组数据中组成10组样本数据。图5所示为塞拉门从润滑良好到故障过程中采集并滤波得到的电流信号，其中横坐标“数据点数”表示采集得到的数字信号的序号。

通过对采集到信号采用sym4进行小波包分解，再分别提取出第3层的8个频率的能量值，最后根据式(1)获得Shannon能量熵值。同时分别提取信号的均方根、峰峰值、偏度指标、峭度指标，劣化过程的部分特征向量见表1、表2。

表1 部分训练样本的Shannon能量熵值

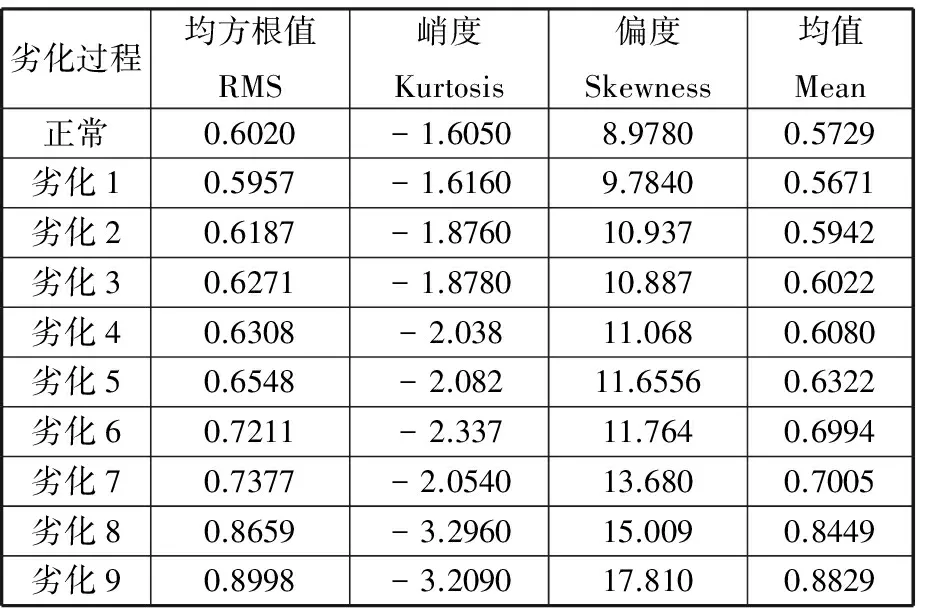
表2 部分训练样本的幅值域指标

3.2 基于SOM-HMC-MC的剩余使用寿命预测分析

首先，将10组全寿命劣化样本分为8组训练集(共166组数据)、2组测试集。其次，通过上述特征提取方法提取出电机电流信号中的多种特征指标，时域为均方根、偏度指标等，频域为Shannon能量熵值。因此，每组数据可用一个1×12的特征向量表示。最后利用SOM自适应聚类能力融合样本特征数据，实现对观测数据的编码，结果见表3。本文设置SOM的最大编码数为6。

为了增加模型的泛化特性，通过建立多观测样本HMC，即选取前8组融合编码处理后的全寿命劣化样本(表3前8行)，并将其用来训练HMC。模型的隐状态数目N=4，观测值数目M=6。通过调整使各观测样本序列等长，且假定每一个观测样本都独立于其他样本。初始条件下，初始状态概率分布矩阵为π=[1 0 0 0]，状态转移概率矩阵A和观测概率矩阵B采用随机方法选取。经过7次迭代训练模型达到收敛(本文中收敛误差设置为0.0001)，训练曲线如图6所示。再用Viterbi算法计算t时刻观察序列下最优的劣化状态，若所获得结果无状态的返跳变或某状态缺失，则认为该模型能够满足实际预测，并获得全寿命下的状态转移矩阵A，这是求取RUL的基础。

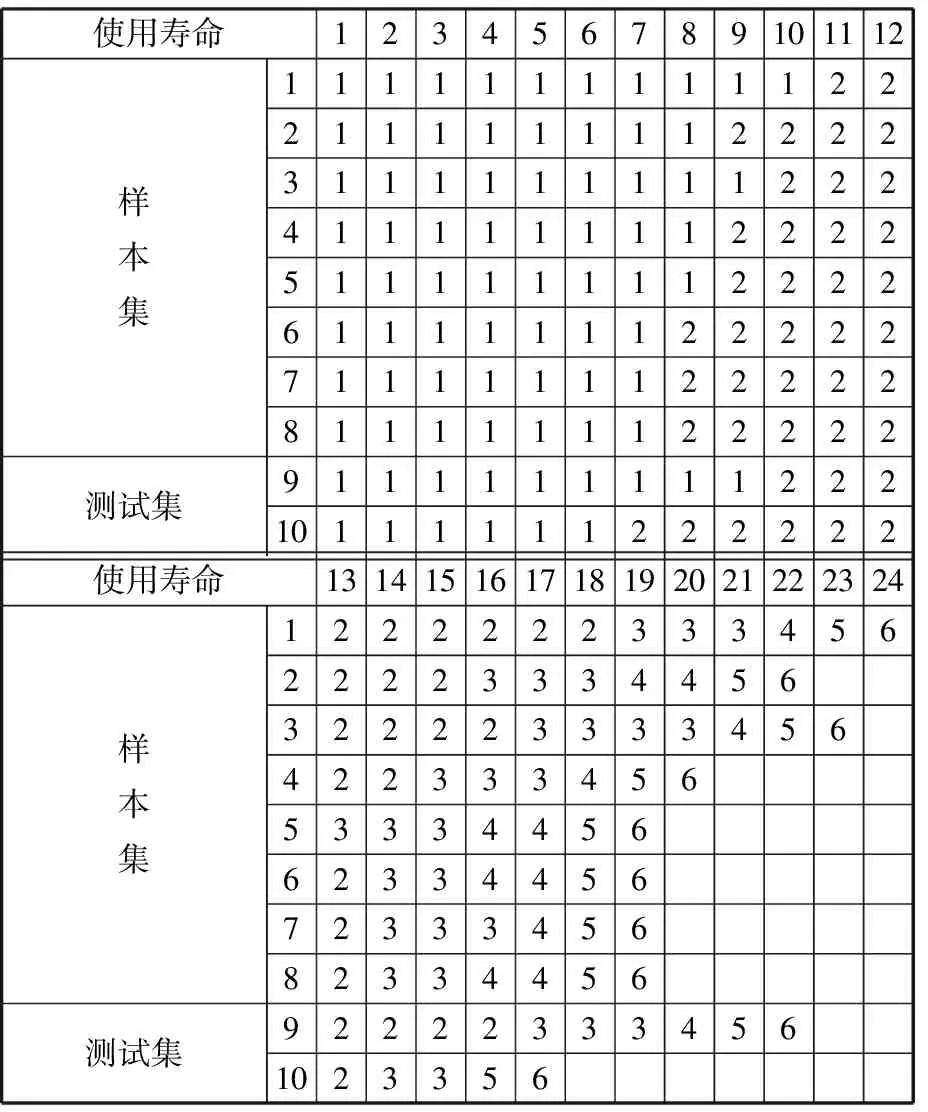
表3 样本特征数据融合编码后的结果

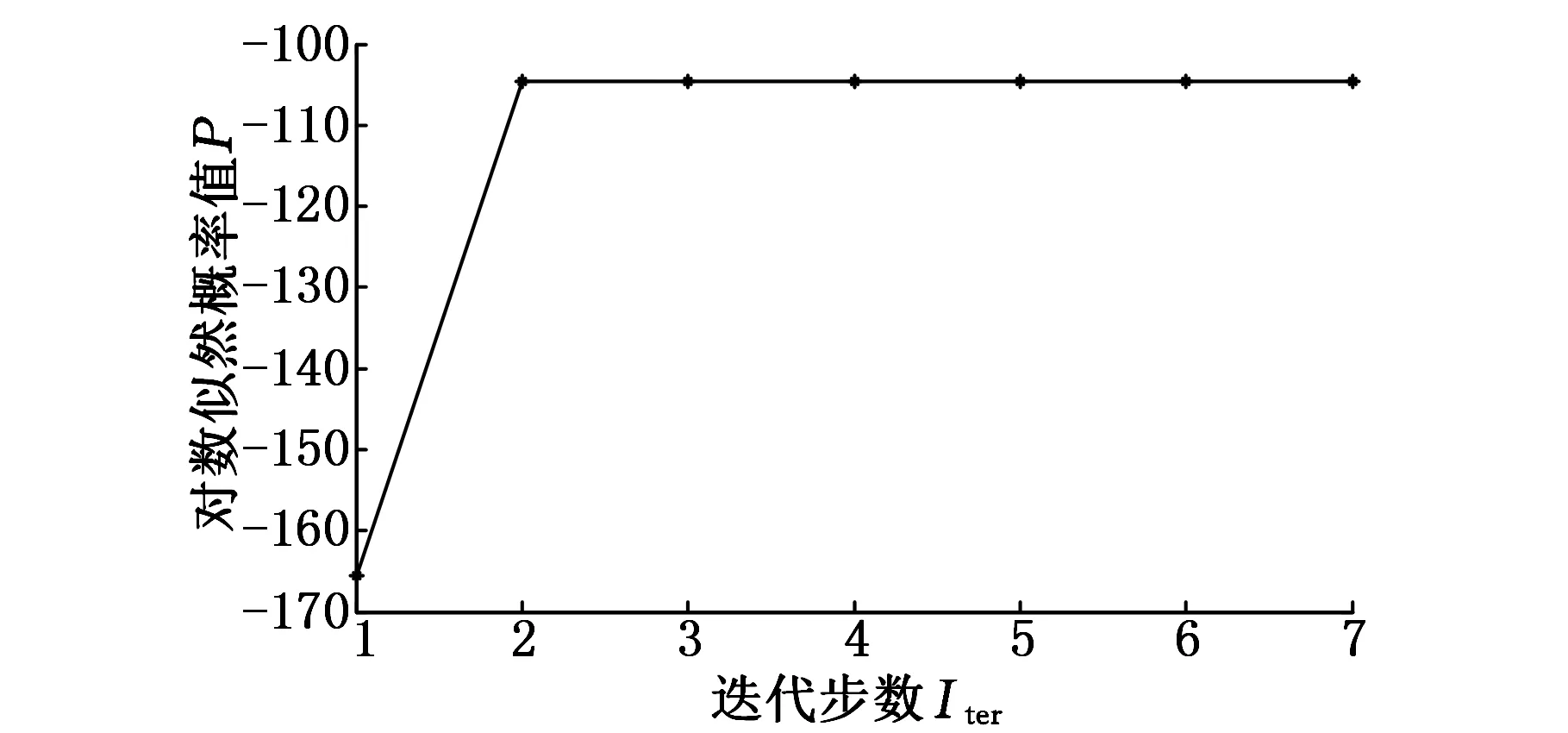
图6 模型参数训练迭代过程

利用已训练好的HMC模型，基于Viterbi算法计算出该观测序列下最优的劣化状态，再根据得到的转移矩阵通过MC仿真获得预测的数据样本，在每次仿真过程中，通过在(0,1)均匀分布产生随机数与状态转移矩阵Aij依次相比较，来决定是否跳变到下一状态。每次获得的下一状态都将作为当前状态，直至到达故障状态。最后通过对转移次数的统计来获得RUL值。

对识别后的状态序列根据Aij进行10 000次MC仿真，可统计得到当前设备的剩余使用寿命概率分布。为了作进一步说明，本文根据全寿命为19的劣化样本1分别提取出其第1，3，6，8，10，12，14，18次开关(推拉)后的数据，给出了其剩余使用寿命概率分布，如图7所示，其中，采集i表示第i次开关(推拉)动作时的剩余使用寿命概率分布。由图7可知，随着设备润滑不良过程的逐渐劣化，RUL的概率分布逐渐减小，RUL的预测精度不断提高。

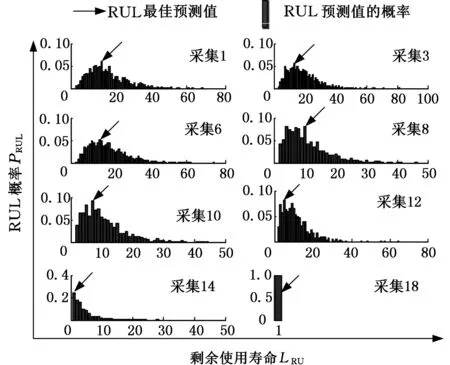
图7 劣化样本1的剩余使用寿命概率分布

为了更有效地估计RUL，对蒙特卡罗仿真得到的预测值给出了其80%置信区间。其预测区间上下限即在所有的RUL的概率分布中最小范围的值。预测区间的公式如下：

(10)

其中，r表示RUL预测值，s表示MC仿真数，b和e分别表示预测下限和上限，cf表示置信区间。本文以样本1为例对其RUL进行预测分析，给出了其80%的置信区间，结果如图8所示。

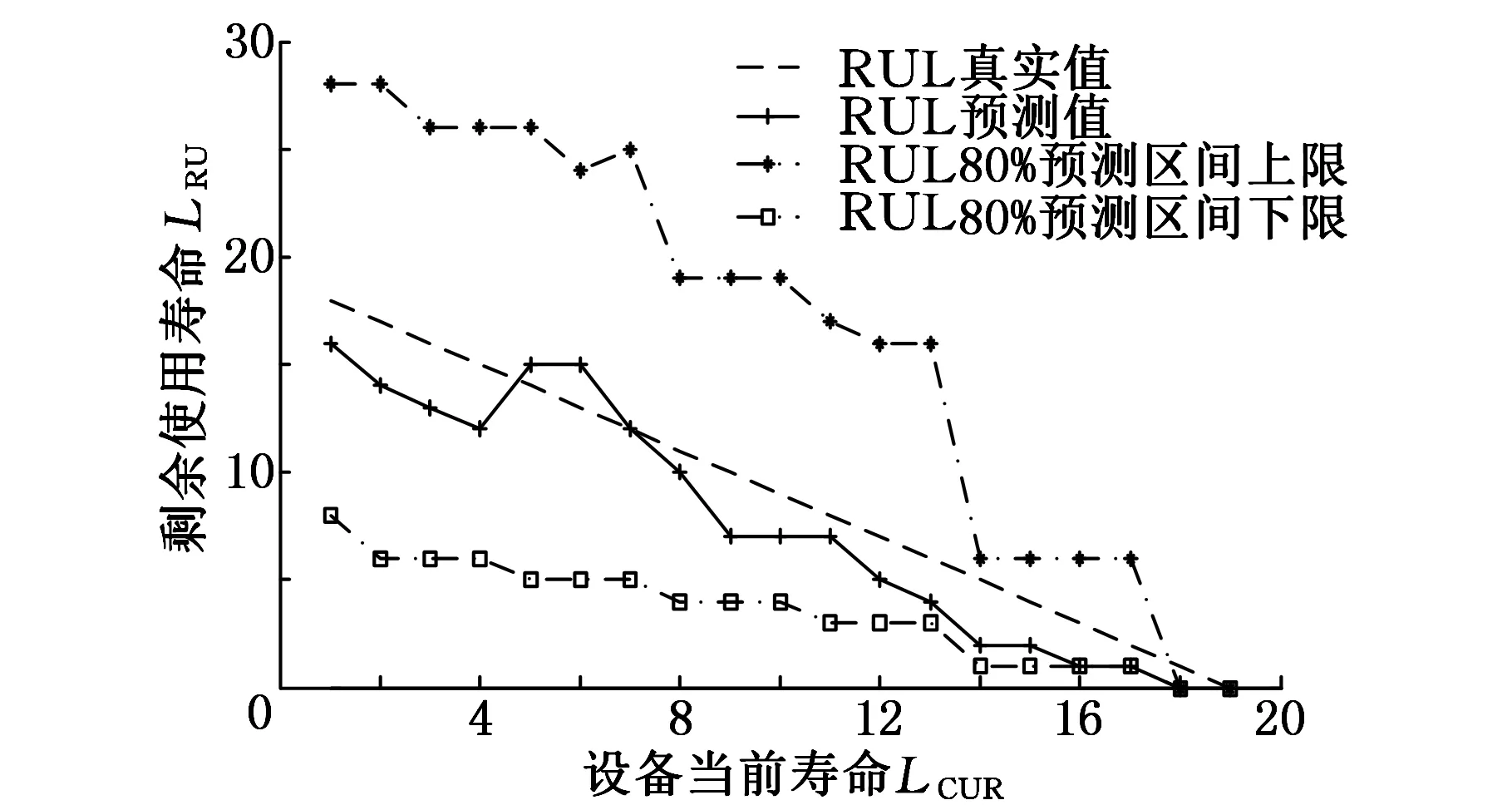
图8 样本1的RUL预测结果

从图8中可看到，设备使用初期，即润滑良好情况下，预测区间的宽度较大，预测精度较差。随着设备在使用过程中润滑不良程度的增加，其预测区间的宽度逐渐减小，预测精度得到了提高，预测结果更接近真实值，表明本文方法的预测结果更具有理论价值。图9分别给出了10组全寿命劣化样本的预测RUL与实际RUL，其中前8组为训练集，后2组为测试集，由于各样本求取预测区间方法与样本1相类似，故不再给出其置信区间。

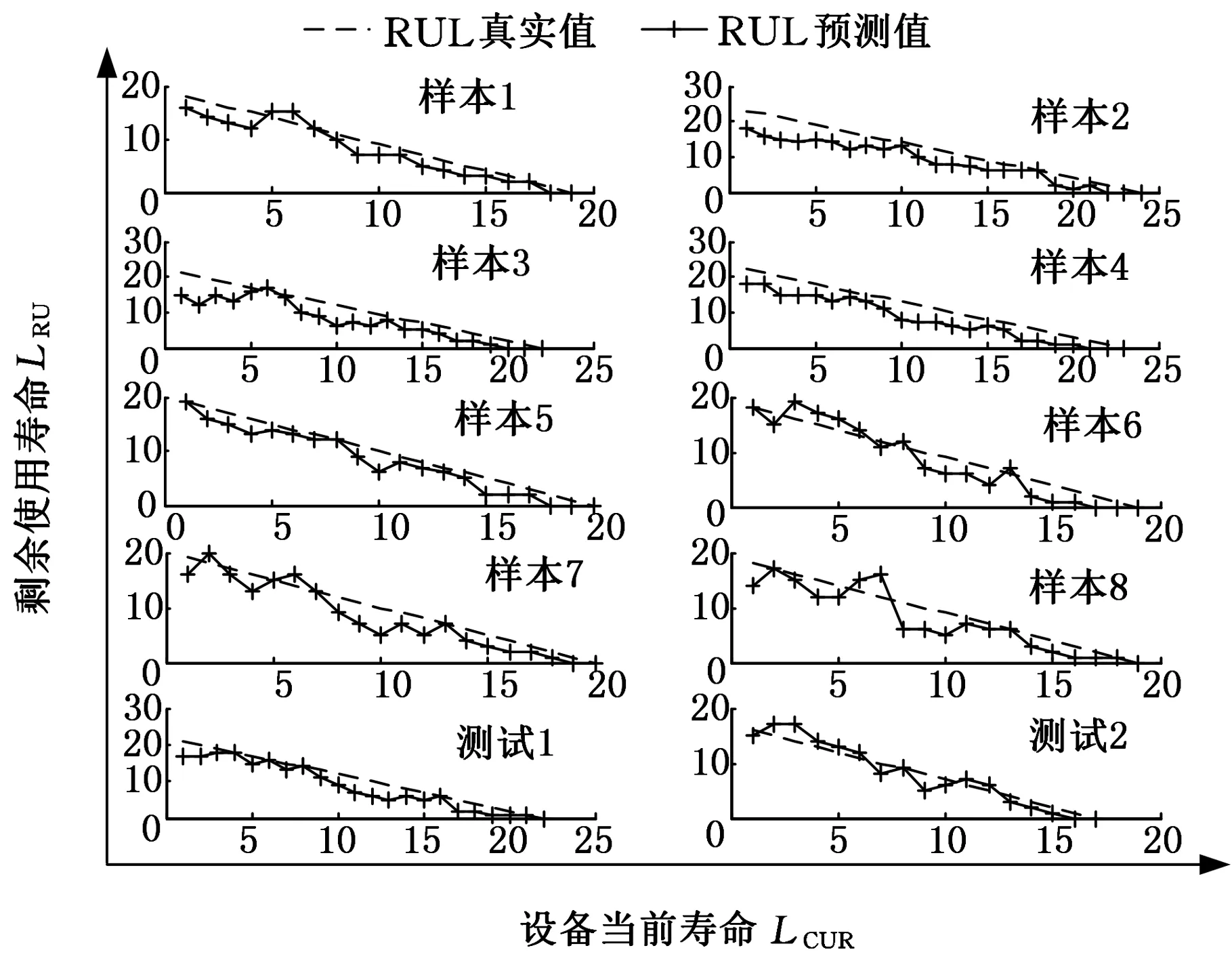
图9 10组电动塞拉门丝杆润滑不良劣化过程剩余使用寿命预测值

从上述预测结果中可看到，本文提出的预测方法对塞拉门润滑不良的故障具有较好的预测效果。为了定量分析，利用式(5)～式(8)所示的平均绝对百分误差、累积相对精度、拟合系数以及均方根误差对测试集预测值进行预测评估[15]。从表4可以看出，模型预测精度较高且具有较高的准确性。模拟实验结果表明，考虑润滑不良情况下，本文方法能较好地实现电动塞拉门丝杆的剩余使用寿命预测。

表4 预测结果性能评估

4 结语

本文在考虑润滑不良故障情况下，提出了一种基于SOM神经网络、HMC模型和MC仿真的地铁电动塞拉门丝杆的剩余使用寿命预测方法。通过人为模拟离散润滑不良劣化过程，采集电机电流信号分别提取时域及时频全寿命下的特征信息组成特征向量；并利用SOM神经网络信息融合特性将所提取的特征信息经过编码融合；再利用其输出结果建立全寿命下的HMC模型，获得全寿命下状态转移矩阵；最后利用蒙特卡罗仿真得到大量预测值，经统计获得最佳RUL预测值。实验结果表明：本文方法能够有效预测在考虑润滑不良时电动塞拉门丝杆的剩余使用寿命。该方法忽略了各劣化状态之间的驻留影响，故今后将引入状态驻留信息来进一步改进本文的预测方法。

[1] 王振东.机械润滑故障分析与预防[J].露天采矿技术, 2003(5):31-32. Wang Zhendong.Failure Analysis and Prevention of Mechanical Lubrication[J].Opencast Mining Technology,2003(5):31-32.

[2] 潘忆宁，夏军，邢宗义，等.地铁车辆车门系统的FMECA分析研究[J].轨道交通装备与技术, 2013(5)：16-19. Pan Yining，Xia Jun，Xing Zongyi，et al. FMECA Analysis of Door System for Metro Vehicles[J].Rail Transportation Equipment and Technology, 2013(5):16-19.

[3] 杨江天，赵明元，张志强，等. 基于定子电流小波包分析的牵引电机轴承故障诊断[J]. 铁道学报，2013,35(2)：32-36. Yang Jiangtian, Zhao Mingyuan, Zhang Zhiqiang, et al.Traction Motor Bearing Fault Detection via Wavelet Packet Analysis of Stator Currents[J].Journal of the China Railway,2013,35(2):32-36.

[4] Langone R, Alzate C, Ketelaere B D,et al.LS-SVM Based Spectral Clustering and Regression for Predicting Maintenance of Industrial Machines[J]. Engineering Applications of Artificial Intelligence,2015,37(37):268-278.

[5] 何群，李磊，江国乾，等.基于PCA和多变量极限学习机的轴承剩余使用寿命预测[J].中国机械工程, 2014,25(7):984-989. He Qun, Li Lei, Jiang Guoqian, et al.Residual Life Predictions for Bearings Based on PCA and MELM[J]. China Mechanical Engineering,2014,25(7):984-989.

[6] 赵洪山, 胡庆春, 李志为.基于统计过程控制的风机齿轮箱故障预测[J].电力系统保护与控制,2012,40(13): 67-73. Zhao Hongshan, Hu Qingchun, Li Zhiwei.Failure Prediction of Wind Turbine Gearbox Based on Statistical Process Control[J].Power System Protection and Control,2012,40(13):67-73.

[7] Dong Shaojiang, Yin Shirong, Tang Baoping,et al.Bearing Degradation Process Prediction Based on the Support Vector Machine and Markov Model[J].Shock and Vibration, 2014,2014(1/2):1-15.

[8] Niu W, Cheng J, Wang G Q,et al.Fast Fault Prediction Model Based on Rough Sets and Grey Model[J]. Journal of Computational and Theotetical Nanoscience, 2013,10(6): 1460-1464.

[9] 孟宗，闫晓丽，王亚超.基于LMD和HMM的旋转机械故障诊断[J].中国机械工程, 2014,25(21):2942-2946. Meng Zong, Yan Xiaoli, Wang Yachao.Rotating Machinery Fault Diagnosis Based on Local Mean Decomposition and Hidden Markov Model[J].China Mechanical Engineering, 2014,25(21):2942-2946.

[10] 蒋永华，程光明，阚君武，等. 基于NGA优化SVM的滚动轴承故障诊断[J].仪器仪表学报,2013,34(12): 2684-2689. Jiang Yonghua，Cheng Guangming, Kan Junwu，et al. Rolling Bearing Fault Diagnosis Based on NGA Optimized SVM[J].Chinese Journal of Scientific Instrument,2013,34(12):2684-2689.

[11] 申弢，黄树红，韩守木，等.基于SOFM网络的机械设备多类型信息融合与状态识别[J].机械工程学报,2001,37(1): 37-41. Shen Tao, Huang Shuhong, Han Shoumu, et al. Multi Type Information Fusion and State Identification of Mechanical Equipment Based on SOFM Network[J]. Journal of Mechanical Engineering,2001,37(1):37-41.

[12] 吴军，邵新宇，邓超. 隐马尔科夫链模型在装备运行可靠性预测中的应用[J].中国机械工程, 2010,21(19): 2345-2349. Wu Jun, Shao Xingyu, Deng Chao.A HMC-based Equipment Operation Reliability Prediction with Multiple Observation Sequences[J]. China Mechanical Engineering,2010,21(19):2345-2349.

[13] Gebraeel N, Elwany A, Pan Jing.Residual Life Predictions in the Absence of Prior Degraduation Knowledge[J]. IEEE Trans. on Reliability,2009,58(1): 106-117.

[14] Eker O F, Camci F, Guclu A,et al.A Simple State-based Prognostic Model for Railway Turnout System[J].IEEE Trans. Industrial Electronics, 2011,58(5):1718-1726.

[15] Szaxena A, Celaya J, Saha A, et al.Metrics for Offline Evaluation of Prognostic Performance[J]. Prognostics and Health Mange, 2010,1(1):2153-2648.

(编辑 陈 勇)

Prediction of Remaining Useful Life for Electrical Sliding Plug Door of Metro Vehicles

Wang Ling Chen Changjun Pan Jing Xu Hong Chen Xiai Na Wenbo

China Jiliang University, Hangzhou，310018

To solve the problems of poor lubrication associated with elecrical sliding plug doors of metro vehicles, a prediction model of the remaining useful life was proposed herein based on self-organizing feature map(SOM), hidden Markov chain(HMC) and Monte Carlo(MC) simulation. Firstly, the motor current signals were collected and the features were extracted. Secondly, the SOM method was used to achieve data fusion and encoding for the multi-dimensional feature data. Then the results were used as input vector of the HMC in order to obtain state transition probabilities for the whole life. Finally, the MC simulation was used to predict the remaining useful life of the degradation process. The fault simulation experimental results show that the method can predict the remaining useful life effectively of the electrical sliding plug door with the consideration of the failure mode of poor lubrication.

electrical sliding plug door; poor lubrication; remaining useful life prediction; hidden Markov chain; self-organizing feature map neural network; Monte Carlo simulation

2015-09-30

国家自然科学基金资助项目(51504228)；浙江省自然科学基金资助项目(LY14F030019, LQ14F050003)

TH17; TP18

10.3969/j.issn.1004-132X.2016.22.003

王 凌，男，1980年生。中国计量大学机电工程学院副教授。主要研究方向为故障诊断、故障预测等。陈长骏，男，1990年生。中国计量大学机电工程学院硕士研究生。潘 静，女，1990年生。中国计量大学机电工程学院硕士研究生。许 宏，男，1966年生。中国计量大学机电工程学院副教授。陈锡爱，男，1981年生。中国计量大学机电工程学院讲师。那文波，男，1963年生。中国计量大学机电工程学院教授。