目标被动测距的引导源方法研究*
2016-12-13李东东
李东东
(杭州应用声学研究所 杭州 310023)
目标被动测距的引导源方法研究*
李东东
(杭州应用声学研究所 杭州 310023)
基于波导不变量的原理,讨论了一种可用于中程目标定位的引导源被动测距法。通过单水听器提取的声场信息,结合波导不变量理论和Hough变换的图形处理方法,实现对目标的被动测距。
波导不变量; 引导源; 被动测距
Class Number TP391
1 引言
海洋环境是一个复杂的波导环境。海洋波导中不同阶之间的简正波,存在加强和减弱的干涉,即声场存在干涉现象。浅海低频声场干涉结构被证明是精细及较稳定的[1]。
浅海环境中的声源定位由于环境本身的复杂性变得十分困难。波导不变量原理最初由俄罗斯学者S.D.Chuprov[2]提出,用于描述相干性中的确定性成分,可以用于表征和解释波导声场中的干涉图像和色散特性等波导环境信息,并可以反演声场中声源的位置信息。
目前计算浅海中波导不变量的方法有:频移补偿[3]、利用 LOFAR 谱图的二维傅里叶变换脊[4]、利用 Hough 变换[5],及深海环境下基于WKBZ[6]等。文献[7]中将波导不变量和虚拟接收器结合,构建水平虚拟接收阵对目标声源进行距离定位;文献[8]中首次提出采用水平阵和引导声源实现目标测距;文献[9]针对实际海洋环境噪声较复杂的情况,提出利用Gabor滤波进行降噪处理来改善目标声源的定位效果;文献[10]为了实现引导源目标定位算法在低信噪比声源信号条件下的准确定位, 提出了利用领域平均法对算法进行降噪处理的方法;文献[11]对于实现引导源目标定位算法在低信噪比声源信号条件下的准确定位, 提出了利用领域平均法对算法进行降噪处理的方法。
本文主要是研究浅海声场中波导不变量的提取方法,并讨论了一种可用于中程被动定位的引导声源被动测距法。该方法主要是基于单个水听器,结合波导不变量以及Hough变换图像处理的方法,实现被动目标的距离估计和跟踪定位。
2 基本原理
2.1 波导不变量提取原理
低频声场具有稳定的干涉结构,在辐射连续谱的宽带声源的接收声功率谱图上,可以观察到稳定的干涉条纹。在高频情况,干涉图可以通过射线理论进行预报;中、低频时,有效的理论是简正波理论,由于干涉条纹复杂,采用波导不变量进行分析较方便。
波导不变量,反映了距离、频率和干涉条纹斜率的关系,描述了声场的频散特性和相消相长的干涉结构。在Pekeris波导中波导不变量β≈1。
波导不变量提取方法就是在低频声场上提取的LOFAR图利用Hough变换,结合与波导不变量有关的干涉条纹方程提取波导不变量[12]。
如图1所示。假定目标声源作匀速直线运动,其线速度为v,接收水听器位于坐标原点,目标声源相对于接收点的最近通过距离为r0,目标声源相对于接收点的最近通过时刻为t0。其中α为航向角(规定与x轴正方向的夹角),θ为目标方位角。

图1 目标运动几何关系图
首先推导第一种干涉条纹公式:
由目标运动几何关系可知:
(1)
(2)
对式(2)求导:
(3)
由波导不变量的定义可知:
(4)
为关于频率f的方程:
(5)
(6)
由上面可以得到:
(7)
整理积分后,得到:
(8)
若是已知干涉条纹顶点频率f0,则f=f(τ),f0=f(0),对上式取反对数可得到:
(9)
推广到一般情况,则有:
(10)
式(10)推导出的是第一种干涉条纹方程,表示的干涉条纹是一族广义双曲线,该方程只适用于干涉条纹顶点已知的情况。若是干涉条纹未出现顶点,则上述方程式不再适用。下面推导不受顶点限制的第二种干涉条纹方程。
第二种干涉条纹公式:
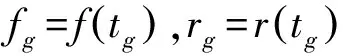
(11)
由图1目标运动的几何关系可知:
(12)

(13)
即第二种干涉条纹方程。若条纹有干涉顶点,则在过顶点的情况下,第二种干涉条纹方程为
(14)
在过顶点条件下,第二种干涉条纹方程与第一种干涉条纹方程一样,都表示一簇广义双曲线;对于远场目标的LOFAR图,第二种干涉条纹方程则近似表示一簇直线。
2.2 波导不变量提取仿真
仿真条件:采用Pekeris模型,海深55m,声速1500m/s,海水密度为1024kg/m3,海底介质声速1749m/s,其密度1941kg/m3,海底无吸收。接收水听器深度:30m。目标等深航行,声源深度:4m,航行速度:12m/s,航向角为30°,最近通过距离:1200m,选取时间段0s~300s,最近通过时间为观测时刻150s。处理频段:300Hz~1000Hz。采用KRAKENC进行简正波模型的声场建模[13]。仿真流程图如图2所示。

图2 参数估计仿真流程图
首先是分析最近通过距离的情况,根据建模后的声场得到目标信号的LOFAR图如图3所示。按照第一种干涉条纹方程,进行Hough变换,得到图4。提取出的信道波导不变量为0.97,目标速度与接收水听器距舰船水平最近距离比v/r0为0.0100。

图3 目标信号的LOFAR图

图4 Hough变换(第一种干涉条纹方程)
按照第二种干涉条纹方程进行Hough变换,结果如图5。提取信道波导不变量β为0.96,航向角为30°。

图5 Hough变换(第二种干涉条纹方程)
按照已知顶点条件下第二种干涉条纹方程进行Hough变换,得到图6。提取信道波导不变量β为0.96,航向角为30°。与Pekeris模型中理论指出的β≈1相比,β偏差为4%。

图6 Hough变换(已知顶点条件下第二种干涉条纹方程)
若是在没有顶点通过的情况下,首先是在没有通过最近距离的情况下得到的声场的LOFAR图以及Hough变换结果,如图7所示。提取波导不变量约为0.98,与在Pekeris模型中理论值相比,偏差为2%,航向角为30°。


图7 未知顶点情况下按照第一种干涉条纹方程仿真图
3 引导源被动定位测距原理
3.1 基本原理
美国物理学者Aaron[14]将提出了一种新的水下定位方法,该算法不需要知道确切的海洋环境的具体参数,而是根据接收到的引导声源信号,与接收的目标声源信号进行处理,从而求得目标声源的距离,有效地克服了环境的时变性的影响。
本节通过水听器接收到来自引导声源和目标声源的声场信号,将得到的LOFAR图进行Hough变换,提取出声场干涉条纹斜率,带入到推导出的测距公式中,求得目标声源的距离。
图8中给出了引导源被动测距声源和接收器的位置关系图。假设海水深度为H,矢量水听器的深度为h,目标声源深度为z0,且目标声源距离接收水听器的水平距离为r1,引导声源的深度以及距接收水听器的水平距离分别为zg和rs。

图8 引导声源被动测距的空间布放图
在引导声源的LOFAR图上的干涉条纹满足方程:
(15)
其中,fs表示引导声源的频率,rs表示引导声源相对接收点的距离,fgs为引导声源的参考频率,rgs为引导声源相对接收点的参考距离,βs为波导不变量。
同样,目标声源的干涉条纹方程为:
(16)
此外,根据波导不变量理论可知:
(17)
假设引导源和目标所处的海洋环境相同,则可以认为:
βs≈β1
(18)
则根据式(17)和式(18)可得:
(19)
其中,dfs/drs和df1/dr1分别为引导源和目标干涉条纹的斜率。
在同一海区,假设海底是平整的前提下,利用引导声源的声场LOFAR图估计出干涉条纹的斜率和波导不变量,结合目标声源的LOFAR图,按照式(19),即可以测得运动目标的距离。
3.2 仿真研究
首先利用单水听器接收一定时间内的引导声源的宽带噪声,获得引导声源的LOFAR图。根据干涉条纹方程,采用Hough变换对引导声源的LOFAR图进行处理,分别提取出干涉条纹斜率和波导不变量。然后再进一步结合目标声源的LOFAR图,估计目标声源的距离。
仿真条件:设海平面为0m,海深为55m,引导声源的深度为4m,引导声源以10m/s的速度航行,接收水听器距离引导声源的水平最近距离P=10m,假设引导声源的位置为[-1000m:10m:-400m],负数表示目标向接收水听器运动。目标声源深度为4m,目标源以15m/s的速度航行,接收水听器距离目标声源的水平最近距离P=100m,设目标声源的位置为[-3600m:15m:-2700m]。接收水听器的深度为30m,频率下限为300Hz,频率上限为2000Hz,采样率为10kHz。

图9 引导声源的LOFAR图

图10 目标声源LOFAR图

图11 目标声源距离随时间变化图
已知目标声源做匀速运动,以20s处的距离为例,此时目标的真实距离是3300m,目标的估计距离是3386m,误差为2.16%。
若是将仿真条件中的引导源深度改为5m,其他条件不变,仿真引导声源被动测距如图12所示。同样以20秒处为例,目标真实距离是3300m,估计距离是3475m,误差为5.23%。

图12 目标声源位置随时间的变化图
4 结语
文中主要研究了基于波导不变量的引导源被动测距。首先是由两种干涉条纹方程,结合Hough变换提取出声场中的波导不变量。然后提出一种基于单水听器通过接收引导声源和目标声源的声场信息,结合波导不变量的知识,就可以实现在海洋环境未知的情况下估计出目标的距离,并进行了真实值和估计值对比验证。
[1] 凌青,生雪莉,袁延艺,等.运动目标低频矢量宽带谱干涉结构及其应用研究[J].声学技术,2012,31(4): 366-369.
[2] S.D.Chuprov. Interference structure of a Sound Field in a Layered Ocean[M]. Acoustics of the Ocean: Current State, Edited by L.M. Brekhovskih and I.B. Andreevoi, Moscow,1982:71-91.
[3] 苏晓星,张仁和,李风华.用频移补偿方法计算声场的波导不变量[J].声学技术,2007,26(6):1073-1076.
[4] 安良,王志强,陆佶人.利用LOFAR谱图的二维傅里叶变换脊计算波导不变量[J].电子与信息学报,2008,30(12):2930-2933.
[5] 田爱玲,刘福臣,周士弘.利用Hough变换提取波导不变量[J].声学与电子工程,2009(4):22-24.
[6] 崔宝龙,笪良龙,徐国军,等.基于WKBZ方法计算深海环境下的波导不变量[J].声学技术,2013,32(4):426-430.
[7] 鹿力成.海底变化环境下目标距离定位[J].水声及物理声学,2007,26(4):65-68.
[8] 赵振东,王大治,王好忠,等.波导不变量原理在目标测距中的应用[J].声学技术,2009,28(2):45-46.
[9] 徐国军,笪良龙,张林,等.基于引导源目标定位算法的降噪处理研究[J].声学技术,2009,28(5):97-98.
[10] 徐国军,笪良龙,李玉阳,等.低信噪比条件下引导源目标定位算法[J].声学技术,2010,29(3):336-339.
[10] 何青海,笪良龙,韩梅,等.声场干涉条纹图像的降噪研究与性能仿真[J].火力与指挥控制,2012,37(6):130-133.
[11] 余赟.浅海低频声场干涉结构及其应用研究[D].哈尔滨:哈尔滨工程大学,2010:124-130.
[12] 温韶娟.中近程目标定位方法研究[D].哈尔滨:哈尔滨工程大学,2011:32-35.
[13] MICHAEL B P.The KRAKEN normal mode program (DRAFT)[M]. LaSpezia: SACLANT Undersea Research Centre,1991.
[14] Aaron M Thode. Source ranging with minimal environmental information using a virtual receiver and waveguide invariant theory[J]. J.A.S.A,2000,108:1582-1594.
Guide Source of Target Passive Ranging
LI Dongdong
(Hangzhou Research Institute of Applied Acoustics, Hangzhou 310023)
Based on the principle of the waveguide invariant, a method for passive ranging which can be used to the source medium range target positioning is discussed. Combined the acoustic field information extracted by a single hydrophone with the theory of the waveguide invariant and the method of Hough transform, the target passive location is realized.
waveguide invariant, guide source, passive ranging
2016年5月10日,
2016年6月16日
李东东,男,硕士研究生,助理工程师,研究方向:水声信号处理。
TP391
10.3969/j.issn.1672-9730.2016.11.033
