大孔径光纤拖曳线列阵阵形估计对目标测向精度的影响*
2016-12-13邱秀分石文峰孙春艳申和平
邱秀分 石文峰 孙春艳 申和平
(北京神州普惠科技股份有限公司 北京 100085)
大孔径光纤拖曳线列阵阵形估计对目标测向精度的影响*
邱秀分 石文峰 孙春艳 申和平
(北京神州普惠科技股份有限公司 北京 100085)
由于舰船机动和洋流的影响,拖曳线阵声呐在水下的阵形畸变会导致探测精度的下降。论文利用姿态传感器测量数据结合二次曲线拟合的方法进行阵型估计,将波束形成后的目标方位结果与GPS测得的目标方位角进行比较。实验室和海试数据分析结果表明,阵形估计后的波束形成的目标方位角较原始阵形估计结果更接近经过修正后的GPS解算目标方位角,最大测向误差不大于2.5°。
光纤水听器; 大孔径拖线阵; 阵形估计; 曲线拟合; 方位修正
Class Number TB565.1
1 引言
随着海洋技术的日益进步,水下基阵逐渐向低频、多基元、长阵列的方向发展。光纤水听器通过光学相干检测将水声振动转化成光信号,再经过传输和信号处理提取出声信号,具有灵敏度高、频带响应宽、稳定性好、便于多路复用的优点,且体积小、重量轻、可远距离测量,使得由其组成的阵列规模更大、探测频率更低。但是由于舰船机动和洋流的影响,拖曳线阵声呐在水下易产生阵形畸变,从而使得后续的信号处理方法不满足直线阵的理论假设,给水下目标的定位方法带来了较大误差。
现有的拖曳阵阵形估计方法主要分为两类:一类是声学的方法,利用阵列接收到的声呐信号进行数据处理,估计出畸变的阵形[1];另一类是非声学的方法,利用安装在阵上的姿态传感器的输出经过多项式拟合得到估计阵形。使用声学的方法一般需要多维的迭代计算,计算量大,收敛速度慢,有时还需要辅助声源的帮助,且校正后的阵型无法验证。利用姿态传感器数据进行拟合的估计方法,无需知道任何先验信息就能确定出各阵元的相对位置,耗时短,可靠性高,更加适合工程实际。饶伟[2]提出了一种基于航向传感器的特征分解的方法,对阵形进行估计,只用少量的航向传感器就能取得较高的估计精度,但是其在估计的过程中会产生误差积累且不易消除。朱沛胜等[3]提出了利用自适应Kalman滤波的方法对拖曳阵阵形进行估计,解决了传统Kalman滤波由于外界作用力和扰动未知导致无法直接应用于阵形估计的问题,但是其输入信息较多,可能会增加实际成本。邢韬[4]提出了一种二次曲线拟合阵形的方法能够快速估计出阵形,但是模型较为简单,未考虑实际使用过程中拖缆长度对测向精度的影响。还有其他学者[5~10]也对此做了相关研究。目前大部分的研究成果都未经海试的验证。
本文在上述基础上,使用二次曲线拟合的方法[4],加入对GPS测算角度校正的过程,利用仿真实验数据和海试数据进行分析,讨论拟合及修正对目标测向精度的影响,发现经过阵形拟合与GPS测算角度修正的处理后,能够有效减小声呐阵的测向误差。
2 目标方位修正方法
2.1 基于二次曲线拟合估计阵形
拖曳线阵在舰船机动和洋流的影响下,会产生一定的阵形畸变,引起测量角度的变化[11]。本文假设阵形的畸变模型近似为圆弧形。

(1)
其中,R表示弧线的半径,η表示阵元偏离本船航向的角度。
本文的理论基础为利用姿态传感器实时得到的航向信息解算得到拖曳线列阵上安装的姿态传感器的斜率,利用二次抛物线拟合这两点间的曲线,求得声呐阵上每个水听器的相对坐标[4]。

图1 阵形畸变模型
2.2 GPS测量目标方位角修正
声呐所显示的目标方位角是以声呐阵中心为参考。声呐阵的阵中心与本船之间有较长拖缆连接,在实际验证测向精度时以目标GPS经纬度与本船经纬度进行解算,而GPS天线与拖缆首部也有一定的空间间隔,如果不考虑这些空间位置误差那么解算出的目标方位角度精度会下降[11]。为了在验证声呐测向精度中具有较精确的理论值,需要将GPS的测算的方位角进行修正与声呐阵测量结果进行联合使用,则需要将目标相对于本船的方位角转化到相对于阵中心上,具体修正模型如图2所示。

图2 GPS解算方位角修正模型
可以观察到θ0为声源相对于本船的方位角,θ为转化后声源相对于阵中心的方位角,βH为船的航向角,βS为阵中心姿态传感器的航向角。
可以得到声源相对于本船的真北方位角:
αAzimuth=θ0+βH(αAzimuth∈[0,360°])
(2)
计算θ1的大小:
θ1=βS-αAzimuth(θ1∈[0,180°])
(3)
最后根据余弦定理:
(4)
可以得出GPS测量得到的声源方位信息转化到以声呐阵中心为原点后的方位角:
(5)
这样就将GPS测得的目标方位角转化到声呐阵中心,以便与声呐信息进行对比。
3 实验验证
3.1 仿真实验设计
为了验证阵形拟合方法的精度,设计了阵形拟合精度的验证实验:假设阵列共10个基元,将三个姿态传感器分别放置阵首、阵中和阵尾,并用柔性细绳连接以阵首的姿态传感器为原点建立XOY直角坐标系,用一根绳索代表阵列,固定每个阵元位置,在绳子上用红标记,将姿态传感器绑在绳子适当的位置上,通过改变绳子形状,记录每次红标记和姿态传感器的横纵坐标,如图3所示。
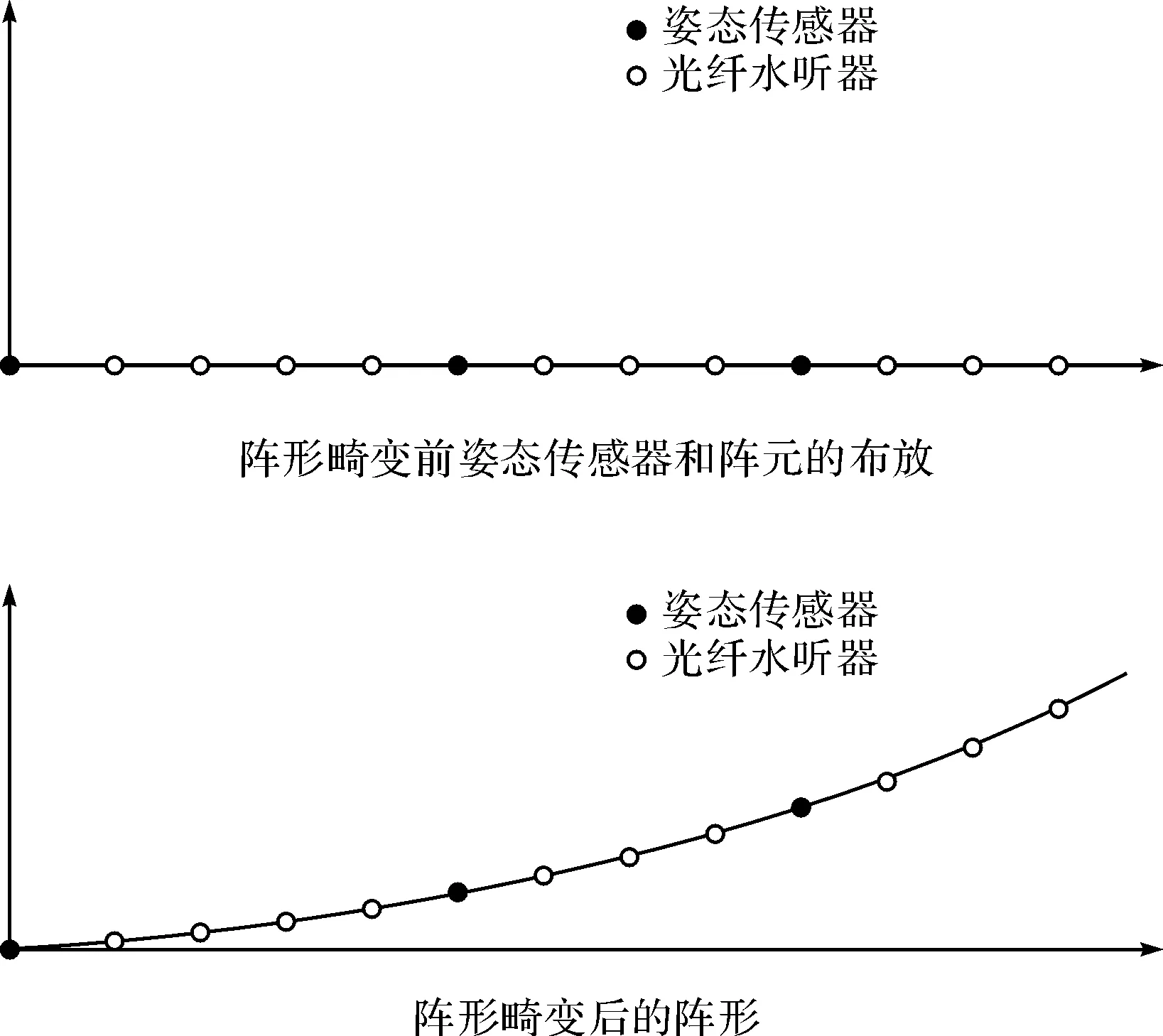
图3 实验装置布放及畸变后的阵形
将直接记录的红色标记的横纵坐标与通过姿态传感器姿态角拟合估计得到的红色标记横纵坐标进行对比,如图4所示。


图4 实际阵形与估计阵形对比
按照同样的方法继续做2组实验,所得的数据如表1所示。

表1 实验室阵形估计实验数据分析
从表1所列出的数据可以看出,估计阵形与实际阵形的误差百分比最大为4.9%。这些误差有部分是由姿态传感器的测量精度不足与人工读数所引入的误差造成的。
3.2 海试实验验证
为了进一步验证该方法的有效性,利用一条大孔径的光纤水听器进行了海上拖曳试验。探测阵中安装了三个姿态传感器,均匀分布在阵列中。声源船与测量船的GPS已知,可以计算得到声源船相对于测量船的方位角。因此将GPS的测算方位角作为参考,来验证阵形估计对测向精度的改善情况。在此,以声源船作为探测的目标船,并且以其发射主动信号的数据作为分析对象。

图5 阵形监控示意图
图5为某一时刻的阵形监控示意图的俯视图,在阵形畸变时,拖曳线列阵的阵首姿态传感器的航向与测量船的航向是不一致的。在接下来的分析中,先利用测量船与声源船的GPS计算出声源船相对于测量船的方位角,然后考虑拖缆的长度,利用阵中心姿态传感器的数据,计算声源船相对于阵中心姿态传感器的方位角。将该方位角作为参考的方位角真值,分别与估计阵形的波束形成角度和未估计阵形的波束形成角度进行比对。
某时刻实验发射了一组脉冲信号,利用测量船与声源船的GPS计算出的声源相对于第一个姿态传感器的方位角为207.1°,目标在左舷。选取脉冲到达时刻进行波束形成,阵形以及波束形成的结果如图6所示。
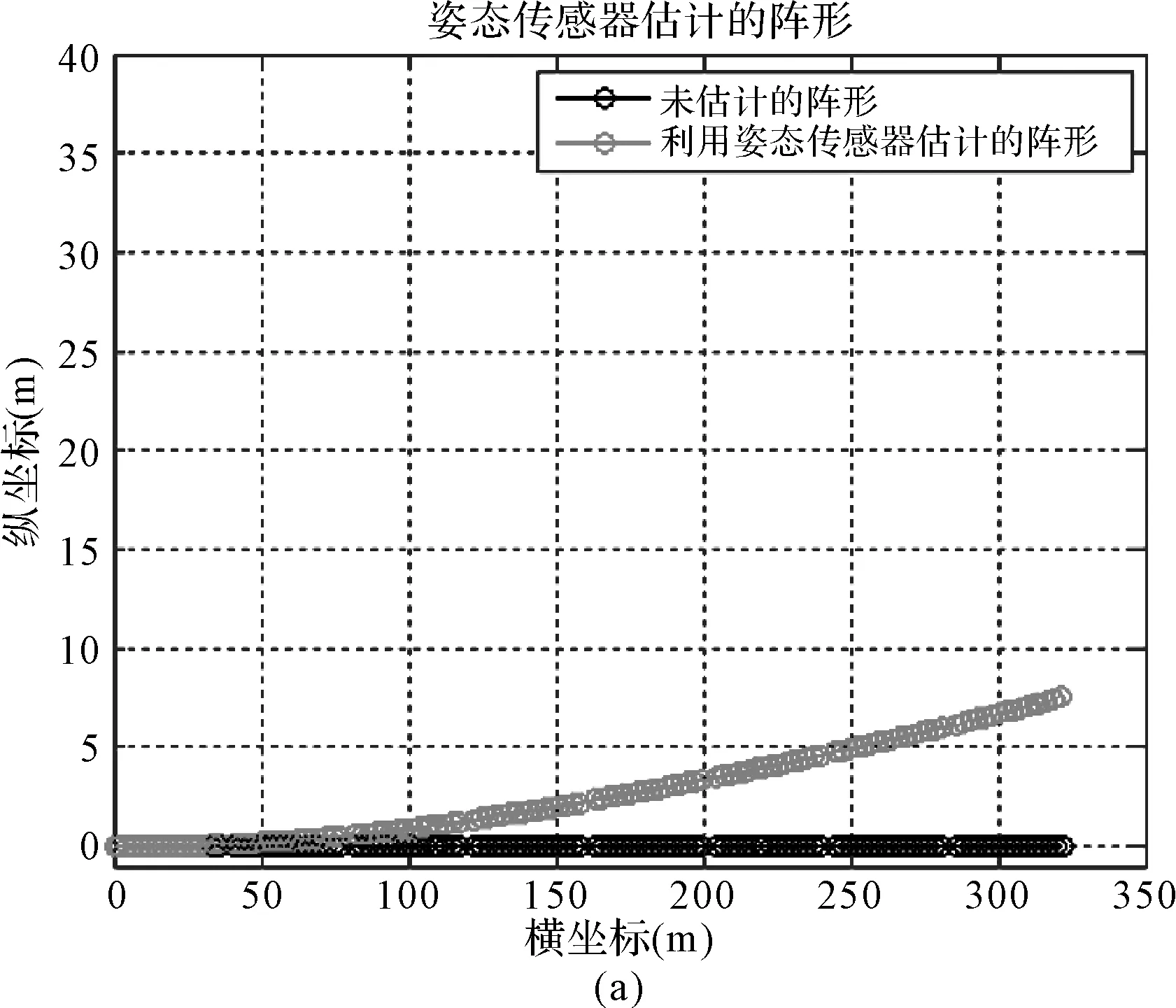

图6 估计的阵形及对测向精度的影响
从图6可以看出,此时阵形偏离了7m左右。利用估计的阵形测得的方位与未估计的阵形测得的方位相差2°,估计的阵形测得的方位更接近于GPS的方位。
再次于另一时刻发射脉冲信号,利用测量船与声源船的GPS计算出的声源相对于第一个姿态传感器的方位角为270.1°,目标在左舷。选取脉冲到达时刻进行波束形成,阵形以及波束形成的结果如图7所示。


图7 估计的阵形及对测向精度的影响
从图7可以看出,此时阵形偏离了16m左右。利用估计的阵形测得的方位与未估计的阵形测得的方位相差4°,同样是估计的阵形测得的方位更接近于GPS的方位。
将海试结果进行汇总,如表2所示。
表2中,未估计阵形时DOA与修正前GPS计算方位偏差为未估计阵形DOA减去修正前GPS计算方位角;未估计阵形时DOA与修正后GPS计算方位偏差为未估计阵形DOA减去修正后GPS计算方位角;估计阵形时DOA与修正前GPS计算方位偏差为估计阵形DOA减去修正前GPS计算方位角;估计阵形时DOA与修正后GPS计算方位偏差为估计阵形DOA减去修正后GPS计算方位角。
从以上分析结果来看,通过姿态传感器进行阵形估计后进行波束形成测得的方位角更接近于GPS修正后的方位角。但是经过阵形估计修正后得到的方位角与GPS计算得到的方位角仍然有最大到8.1°的误差。本次海试声呐阵列长达数百米,拖缆长度更是接近千米。GPS测得的目标方位是以GPS为原点,声呐信息算得的目标方位是以声呐阵中心为原点,由于两个中心距离较远,使得两类信息计算的得到的方位角会有较大的偏差。

表2 经过阵形估计前后目标方位角对比
利用缆长、阵长、GPS测得的本船航向角、阵中心姿态传感器输出的航向角信息,将GPS测得的目标方位角修正到声呐阵中心再进行对比。进行修正后的GPS测量目标方位角与声呐阵计算得到的目标方位角的偏差大大减小,最大误差只有2.5°。这说明对于GPS测量得到的方位角进行修正是十分必要的。
4 结语
通过实验室实验与实际海试数据分析表明:相较于未进行阵形估计,利用姿态传感器数据进行阵形估计修正能够有效提高波束形成计算得到的目标方位角的精度;且将GPS测得的目标方位角转化到声呐阵中心,可使声呐的测向结果与GPS测向结果更加吻合。同时考虑阵形畸变与中心点偏移的误差,将更加贴近于工程实用。
[1] 李建,高明生,解恺.线阵阵形畸变对目标方位估计性能影响及校正分析[J].南京大学学报(自然科学),2015,51(6):1195-1202.
[2] 饶伟,倪明,梁迅,等.利用航向传感器的特征分解阵形估计方法[J].声学技术,2007,26(5):59-60.
[3] 朱沛胜,黄勇,张扬帆,等.拖曳阵阵形估计的自适应Kalman滤波算法[J].声学技术,2007,26(1):1-5.
[4] 邢韬,林晋美,蔡惠智.适用于声呐阵形估计的姿态传感器网络设计[J].应用声学,2008,27(1):42-48.
[5] 安良,陈励军,陆佶人,等.船载柔性阵基元坐标实时获取技术研究[J].数据采集与处理,2010,25(1):86-92.
[6] 赵学伟.阵列误差对DOA估计的影响及校正[D].成都:电子科技大学,2008.
[7] 李启虎.论阵形畸变的拖曳式线列阵的工作方式的选取问题[J].声学学报,1991,16(1):31-36.
[8] 李启虎.数字式声纳设计原理[M].合肥:安徽教育出版社,2002.
[9] Gerstoft P, Hodgkiss W S, Kuperman W A, et al. Adaptive beamforming of a towed array during a turn[J]. IEEE Journal of Oceanic Engineering,2003,28:44-53.
[10] Howard B E, Syck J M. Calculation of the shape of a towed underwater acoustic array[J]. IEEE J.Oceanic Eng.,1992,17:193-203.
[11] 邹晓春,曹焱.主动拖曳线列阵声呐系统测向误差的分析与修正[J].声学与电子工程,2011(3):4-6.
Influence of Shape Distortion of Large-aperture Optical Fiber Towed Array on Precision of DOA
QIU Xiufen SHI Wenfeng SUN Chunyan SHEN Heping
(Appsoft Technology Co.Ltd, Beijing 100085)
Affected by the ship movement and ocean current, towed linear sonar array would occur shape distortion underwater, which leads to a decline in detection precision. This paper combines posture sensor data and quadratic curve fitting method to estimate the distorted array shape. Then it makes the comparison between the calculated target angle by beamforming and fixed GPS-calculated target angle. The analysis of laboratory experiment and sea trial data shows that the calculated target angle by beamforming with shape correction is closer to the fixed GPS-calculated target angle than without shape correction. Maximum error is less than 2.5°.
optical fiber hydrophone, large-aperture towed array, array shape estimation, curve fitting, direction fixing
2016年5月16日,
2016年6月30日
国家重大科学仪器设备开发专项资助项目(编号:2013YQ140431)资助。
邱秀分,女,工程师,研究方向:水声信号处理。石文峰,男,工程师,研究方向:水声信号处理。孙春艳,女,工程师,研究方向:水声信号处理。申和平,男,高级工程师,研究方向:水声信号处理。
TB565.1
10.3969/j.issn.1672-9730.2016.11.012
