基于动态规划的E-REV能量管理策略研究

席利贺，张 欣，孙传扬

(北京交通大学 机械与电子工程学院，北京 100044)



基于动态规划的E-REV能量管理策略研究

席利贺，张 欣，孙传扬

(北京交通大学 机械与电子工程学院，北京 100044)

增程式电动汽车动力来源于增程器与动力电池，车辆运行过程中如何在两者之间分配需求功率，使得整车在行驶过程中燃油经济性最好，是增程式电动汽车能量管理策略核心的问题.提出一种基于动态规划的增程式电动汽车能量管理策略，运用动态规划对整个工况增程器与动力电池输出功率分配比例进行优化.欧洲标准行驶工况(NEDC)组合行驶工况的仿真结果表明:相比实车采用的恒温器式控制策略，基于动态规划的能量管理策略整车燃油经济性提高12.6%.

增程式电动汽车；动态规划；能量管理策略；优化

面对全球环境恶化及化石燃料的枯竭，政府和环保部门对整车燃油消耗及排放的要求越来越严格[1]，迫使世界各国大力发展纯电动汽车(Electric Vehicle, EV)和混合动力汽车(Hybrid Electric Vehicle, HEV)[2].但纯电动汽车续驶里程及电池循环使用寿命限制了纯电动汽车的发展，为此国内外生产厂商和研究机构推出了增程式电动汽车的解决方案[3].

增程式电动汽车(E-REV)可以从外界电网获取电能并存储在动力电池中，大部分工况下，以纯电动模式行驶，可以实现“零污染和零排放”[4]；在动力电池电能不足时，也可以通过一个发动机联接发电机的增程器延长续驶里程.在需求功率较大的行驶工况下，增程器还可以和动力电池协同驱动整车，因此成为混合动力汽车的研究热点[5-6].

将需求功率在动力电池与增程器之间进行合理分配属于能量管理策略范畴，是整车控制器的核心内容.国内外有关能量管理策略的研究主要分为基于规则的能量管理策略，基于静态优化设计的能量管理策略，以及全局优化能量管理策略[7-8].其中，基于规则的能量管理策略依据工程经验或专家知识库制定增程器启停逻辑，整车实时控制效果最好，但并不能获得最佳燃油经济性与排放特性.基于静态优化设计的控制策略是寻找每一时刻等效燃油消耗量最小的控制量，计算量较大，且不能达到全局最优.全局优化能量管理策略采用全局优化理论，对指定工况下的能量分配进行优化，不能用于实时控制，但可作为评价其他控制策略的基准.本文作者运用动态规划算法设计增程式电动汽车能量管理策略，以燃油花费与电能花费为代价函数，仿真结果表明:所设计的控制策略相比于实车采用的恒温器式控制策略经济性有明显提高.

1 E-REV动力系统结构

本文研究的E-REV的动力系统结构如图1所示.发动机通过与启动发电一体化发电机(Integrated Starter Generator,ISG)联接组成增程器.取消传统起动机，在启动时，由ISG拖拽发动机.增程器与电池通过功率转换器为驱动电机提供电能.驱动电机与车轮之间通过单极主减速器连接.

2 基于动态规划的能量管理策略

大部分增程式电动汽车实车上采用恒温器式控制策略，所定的规则是基于实际工程经验，不能达到全局优化的效果，需要采用优化理论设计混合动力控制策略.而E-REV的能量管理策略优化是带有约束条件的非线性系统优化问题[9]，可以借助动态规划多阶段决策的特点解决此类问题.图1中各动力系统部件参数见表1.其中:主减速比为7.793;整车装备质量为1 400 kg.

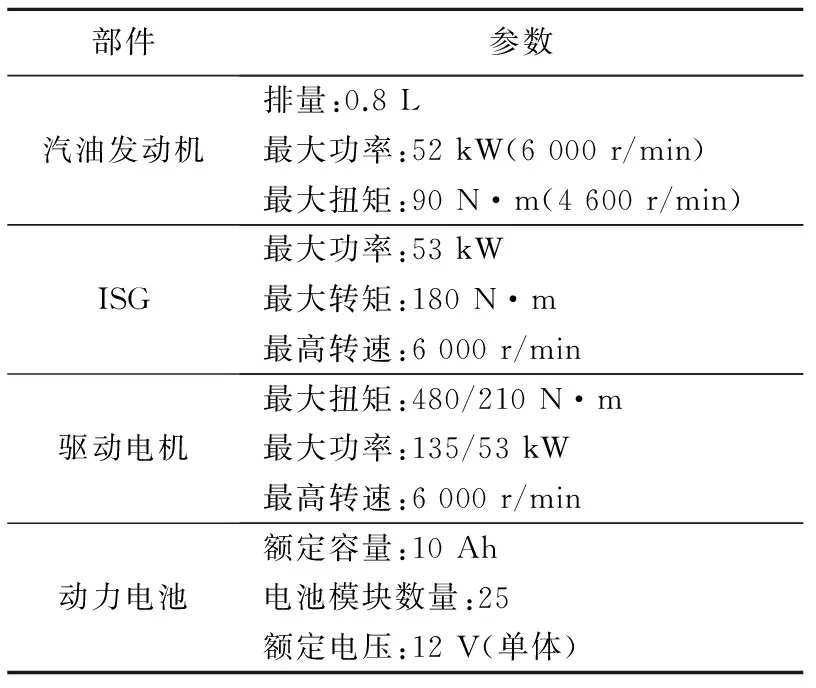
表1 动力系统部件参数Tab.1 Parameters of dynamic system

2.1 E-REV系统仿真数学模型

2.1.1 整车动力学模型

运用纵向动力学，将E-REV看作质点，整车需求功率模型为

(1)

式中：ηt为动力传动系效率；δ为旋转质量换算系数；M为整车质量；v为行驶车速；g为重力加速度；f为滚动阻力系数；CD为风阻系数；A为迎风面积.

2.1.2 增程器模型

增程器是利用发动机燃料化学能输出的机械能通过ISG转化为电能的装置.增程器是发动机与发电机协调工作的系统，增程器工作点的选取要结合发动机最优经济区域和发电机高效率区域.以往建立的增程器模型将ISG发电效率设为定值，选取发动机燃油经济性最佳点作为增程器运行的工作点，此种建立方法不能使增程器系统燃油消耗达到最优且输出电功率,由于电机发电效率的不同而产生输出功率不足等问题，造成整车控制器能量管理策略控制不精确.因此，本文考虑发电效率随工作点变化，选取增程器发电效率最高点作为增程器工作点.定义增程器发电效率为

(2)

式中: ηeng为发动机工作效率;ηISG为ISG发电效率,是转速与转矩工作点(ω,τ)的查表函数.

由图1可以看出，发动机与ISG为同轴串联，可近似认为增程器在运行过程中，发动机与ISG为同一转速与扭矩工作点.

发动机工作效率为

(3)

式中: Peng为发动机输出有效功率;Pfuel为所消耗燃油热能功率，可以通过下式求出

(4)

采用上述方法，在每一转速下寻找增程器发电效率最高工作点，不同转速所对应的增程器发电效率最高工作点组成增程器最优工作曲线.

图2为增程器所采用发动机的燃油消耗图，图中虚线部分为所选取的增程器最优工作曲线，实线为发动机最优工作曲线，其中发动机最优工作曲线是以发动机燃油消耗最优为目标，未考虑增程器发电效率.从图2中可以看出，增程器最优工作曲线与发动机最优工作曲线的变化规律不同，这是因为发动机最优工作曲线虽然能够保证燃油消耗最低，但并不是增程器发电效率最高点.本文选取的增程器最优工作曲线转矩波动范围不大，有利于发动机进行调速控制.

2.1.3 动力电池模型

本文采用动力电池内阻模型，等效电路图如图3所示.

内阻模型中的电流通过下式计算得到

(5)

式中: Ib为电池电流；voc为电池开路电压；Rint为电池等效内阻；Pb为电池电功率，正值代表放电，负值代表充电.

2.2 动态规划问题建立与求解

动态规划是运筹学的一个分支，是求解决策过程(Decision Process,DP)最优化的数学方法，利用各阶段之间的关系，逐个求解，是一种多阶段决策优化算法，针对E-REV能量管理策略建立动态规划问题,其优化原理如图4所示.

2.2.1 选取状态量

状态量需要能够正确描述被研究对象的历史特征，且具有无后效性的特点.但动态规划计算量与被控对象的状态量数目呈指数关系，为此，不考虑动态响应频率高于增程式电动汽车能量流的状态变量[10].因此，本文选取动力电池SOC作为本文的状态量，即

x(k)=[SOC]

(6)

2.2.2 选取控制量

控制量是导致被控对象由前一状态到当前状态的诱因，每个阶段的控制量只需要考虑当前状态且具有无后效性的特点，多阶段的控制量组合在一起就是控制策略.由于增程器输出电功率直接决定动力电池SOC的变化，因此本文将增程器输出电功率作为控制量，即

u(k)=PAPU

(7)

2.2.3 状态转移方程

状态转移方程用来描述当前状态量与前一时刻状态量与控制量之间的关系.本文的状态转移方程为

SOC(k)=SOC(k+1)+Ib

(8)

式中：SOC(k)为当前状态动力电池SOC；SOC(k+1)为下一时刻动力电池SOC.

2.2.4 约束条件

状态量和控制量均无后效性，对多阶段决策问题进行优化，需要针对被控对象特点，选取边界条件，形式为等式约束和不等式约束.本文选取的边界条件为：

1)系统约束条件：

Pb=Pm_req-PAPU

(9)

2)动力系统部件物理约束条件：

(10)

式中:Pb,chg、Pb,dis分别代表电功率充放电限制；Tm为驱动电机扭矩；TAPU、ωAPU为增程器转矩和转速，受到发动机和ISG的限制.

3)其他约束条件

考虑到部件耐久性等因素，防止增程器频繁启动造成油耗增加，动力电池充放电持续时间较短对电池的损害等.将工作持续时间加入到约束条件当中

tdur_APU≥tmin_APU

(11)

tdur_batt≥tmin_batt

(12)

式中:tdur_APU为增程器持续工作时间，选取最低持续时间tmin_APU为6 s[11]；tdur_batt为动力电池持续充放电时间，选取最低持续时间tmin_batt为20 s.

2.2.5 代价函数

代价函数是多阶段优化问题的目标函数.由于较长的纯电动续驶里程，单以燃油消耗为优化目标描述系统能量消耗，并不适用于E-REV，因此本文以E-REV动力系统能量损耗最小为优化目标，所构建的代价函数为

(13)

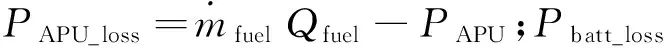
2.2.6 动态规划求解

本文取时间间隔Δt=1 s，SOC离散精度为5×10-4，初始动力电池SOC确定情况下，以代价函数式(13)为目标，采用正向求解方式，寻找整个循环工况的最优控制序列[u*(0),u*(1)，…，u*(k)，…，u*(N-1)]，具体求解步骤如下：

第0时刻(初始阶段)

(14)

第k时刻(1≤k≤N-1)

(15)

3 仿真结果及分析

本文研究的E-REV在NEDC工况下纯电动续驶公里为50 km，为研究整车进入增程模式后对比不同能量管理策略之间燃油经济性的优劣，需要对工况进行组合，取10个NEDC组合工况，作为本文仿真的循环工况，总公里为105 km，见图5.

本文所研究的E-REV实车中采用恒温器式控制策略，该策略以动力电池SOC为判别条件，当动力电池SOC达到预设门限值时，控制增程器启动，发动机工作在燃油消耗最低点，保持恒定电功率输出.按照上述原则，设定增程器输出功率为24.5 kW，动力电池SOC上下限分别为0.7和0.3.

将原车恒温器式控制策略与本文提出的控制策略分别采用组合工况进行仿真计算，其仿真结果如图6～图9所示.

从图6中可以看出，恒温器式控制策略所选定的工作点不在增程器最优工作曲线上，这是因为恒温器式控制策略选定工作点以发动机燃油消耗最低为原则，不考虑ISG发电效率，使得所选定的工作点并不是增程器发电效率最高点.基于动态规划的控制策略能够很好的沿着增程器最优工作曲线工作，证明控制策略的有效性.

分析图7～图9可以看出，两种策略在动力电池SOC降到下限SOCmin之前，均采用纯电动模式行驶.随后增程器启动，进入增程模式.其中，恒温器式控制策略下，控制增程器在首先满足整车需求功率的要求下，富余功率为电池充电.动力电池SOC由A点放电到B点输出电能为2.57 kW·h，由B点充电到C点，所需充电电能为3.49 kW·h.这是由于动力电池内阻的影响，外界充电电能并不能完全被电池吸收.而相比恒温器式控制策略，基于动态规划的能量管理策略在进入增程模式后，控制增程器为动力电池充电的电功率相对较小，可知增程器尽量避免为电池持续充电.由前面分析可知，为电池充电的能耗较高，引起的电池充电热能损耗也会增加，所以为了尽量避免能量损耗，增程器只承担驱动电机处需求功率.

在仿真结束时，两种控制策略动力电池SOC值不相同，为了对比两种策略的燃油经济性优劣，引用等效燃油消耗评价方法[12]，统计结果如表2所示.

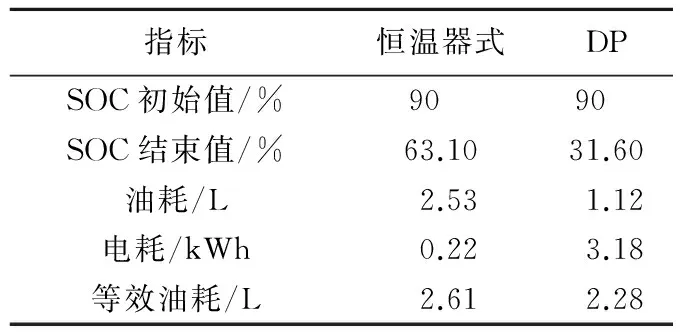
表2 仿真结果对比Tab.2 Comparisons between two strategies

从表2可以看出，基于动态规划的能量管理策略燃油经济性提高12.6%，可见，基于动态规划的能量管理策略能够有效地降低等效燃油消耗.

4 结论

1)能量管理策略是开发混合动力车辆的核心技术之一.本文作者提出了一种基于动态规划算法的能量管理控制策略设计方法，并应用在增程式电动汽车上，将燃油花费与电能花费之和作为代价函数，求解整个工况下的最优控制解.

2)NEDC组合仿真工况结果表明：恒温器式策略在动力电池不足时，使用增程器为电池充电的过程中，由于动力电池自身内阻的影响，使得增程器为动力电池提供的电能不能完全被利用，增加了能量损耗.

3)基于动态规划的能量管理策略在整车进入增程模式后，控制增程器承担整车需求功率，降低为动力电池充电的电功率，燃油经济性提高12.6%，为进一步的实车能量管理策略改进提供了理论依据.

[1] WIRASINGHA S G, EMADI A. Classification and review of control strategies for plug-in hybrid electric vehicles [C]. Vehicle Power and Propulsion Conference, 2011:907-914.

[2] 靳彪,张欣,杨庆宝.纯电动汽车低速转向差速控制模型[J].北京交通大学学报,2013,37(4):158-161. JIN Biao, ZHANG Xin, YANG Qingbao. Low speed steering differential control model for pure electric vehicle[J]. Journal of Beijing Jiaotong University,2013,37(4):158-161. (in Chinese)

[3] TATE E, HARPSTER M O, SAVAGIAN P J. The electrification of the automobile: from conventional hybrid, to plug-in hybrids, to extended-range electric vehicles[J]. SAE International Journal of Passenger Cars - Electronic and Electrical Systems, 2009, 1(1):156-166.

[4] 牛继高,司璐璐,周苏,等.增程式电动汽车能量控制策略的仿真分析[J].上海交通大学学报, 2014, 48(1) :141-145. NIU Jigao, SI Lulu, ZHOU Su, et al. Simulation analysis of energy control strategy for an extended-range electric vehicle[J].Journal of Shanghai Jiaotong University，2014, 48(1):141-145.(in Chinese)

[5] MATTHE R, TURNER L, METTLACH H. VOLTEC battery system for electric vehicle with extended range[J]. SAE International Journal of Engines, 2011, 4(1):1944-1962.

[6] BASSETT M, FRASER N, BROOKS T, et al. A study of fuel converter requirements for an extended-range electric vehicle[J]. SAE International Journal of Engines, 2010, 3(1):631-654.

[7] 顾杰.增程式电动汽车能量管理策略研究[D].合肥：合肥工业大学,2013. GU Jie. A study on energy management control strategy for extend rangeelectric vehicle[D].Hefei: Hefei University of Technology,2013. (in Chinese)

[8] TORRES J L, GONZALEZ R, GIMENEZ A, et al. Energy management strategy for plug-in hybrid electric vehicles： A comparative study[J]. Applied Energy,2014,113(6):816-824.

[9] 申彩英, 夏超英. 基于改进型动态规划的串联混合动力汽车控制策略[J]. 控制理论与应用, 2011, 28(3):427-432. SHEN Caiying, XIA Chaoying.Control strategy of series hybrid electric vehicle based on improved dynamic programming[J].Control Theory & Applications,2011, 28(3):427-432.(in Chinese)

[10] 邹渊, 侯仕杰, 韩尔樑,等. 基于动态规划的混合动力商用车能量管理策略优化[J]. 汽车工程, 2012, 34(8):663-668. ZOU Yuan,HOU Shijie,HAN Erliang, et al.Dynamic programming-based energy management strategy optimization for hybrid electric commercial vehicle[J].Automotive Engineering,2012,34(8):663-668.(in Chinese)

[11] CHEN B C, WU Y Y, TSAI H C. Design and analysis of power management strategy for range extended electric vehicle using dynamic programming[J]. Applied Energy, 2014, 113(1):1764-1774.

[12] 轻型混合动力电动汽车能量消耗量试验方法：GB/T 17953—2005[S].2005. Test methods for energy consumption of light-duty hybrid electric vehicles：GB/T 17953—2005[S].2005. (in Chinese)

Energy management strategy for E-REV based on dynamic programming

XILihe，ZHANGXin，SUNChuanyang

(School of Mechanical,Electronic and Control Engineering, Beijing Jiaotong University, Beijing 100044,China)

Range-extender and battery are the main energy sources for Extended-Range Electric Vehicle (E-REV). In order to improve fuel economy, the power demand distribution between range-extender and batteryare the main problem for energy management strategy. This paper considers an energy management strategy for E-REV using dynamic programming, which optimize the power split between range extender and battery under whole driving cycle. Simulation results using combined New European Driving Cycle (NEDC) cycles show that the proposed control strategy has improved fuel economy about 12.6% compared to that of the thermostat control strategy.

extended-range electric vehicle; dynamic programming; energy management strategy; optimization

2015-12-11

中央高校基本科研业务费专项资金资助(2014YJS119)

席利贺(1988—)，男，北京人，博士生.研究方向为混合动力汽车能量管理策略. email:xilihe@bjtu.edu.cn.

张欣(1959—)，女，湖北天门人，教授，博士，博士生导师.email:zhangxin@bjtu.edu.cn.

U469. 72

A

1673-0291(2016)05-0120-06

10.11860/j.issn.1673-0291.2016.05.021