构建关注数学思想发展的高效灵活课堂

何彩明

当前，部分教师在进行情境创设时，忽视了现实情境背后所隐含的数学线索，干扰和弱化了学生数学思维的发展，忽视数学本源性问题，以致在数学教学中“冲淡”教学目标。本文就以“数学广角”的教学为例，谈一谈小学数学情境化教学的实践。

一、挖掘教材，突出思想性

现行人教版教材中，安排了很多主题图和小插图，很多地方已不再对知识点的最后结论下定义，只在重点关键处加以提示和引导，就如，“从上面的算式中，你发现了什么规律？”“想一想：还有其他的方法吗？”“自己试一试，你是怎么想的？”等，引导学生对特殊实例的观察、试验、分析、归纳、抽象、概括，经历探索推理的心智活动过程。改变后的教材，实际上要求教师要站在更高的水平准确把握学生的新知生长点和最近发展区，理清教材的知识体系，读懂教材的编排意图和要挖掘的思想内涵。同时，这也要求加强学生解读文本信息的能力，提高其思维密度，也为他们的“后劲”打下基础。曾听过一位教师执教人教版六上“数与形”一课，他在处理数和形这两个不可分离的数学表象时，巧妙处理数与形的互相转化，将数与形的思想教学分解为以形助数、以数解形、数形结合三个环节逐渐展开。

【教学片段】

一、以形助数

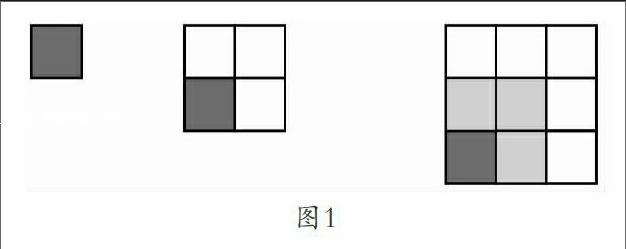
1. 请同学们认真观察，看一看这三幅图有什么规律？（图1）

2. 请大家认真观察这些图和算式，有什么发现？

3. 按这样的顺序，下一个图形和算式会是什么样的？请你们用彩笔在老师提供的方格纸上画一画、涂一涂。哪种画法更好？为什么？

4. 下面我们就利用规律来写一写。

1+3+5+7+9+11+13=（ ）

1+3+5+7+5+3+1=（ ）

1+3+5+7+9+11+13+11+9+7+5+3+1=（ ）

5. 小结：看来有的计算问题借助图形思考更容易。

二、以数解形

1. 计算问题可以借助图形思考，那图形的问题是不是也能借助数来解决？请同学们看看这四幅图（教材P108“做一做”第2题），有什么规律？

2. 如果不画图，照这样下去你知道第6个图形和第10个图形各有多少个红色和蓝色的小正方形吗？

3. 回顾：看来图形的规律问题也可以借助数来解决。我们利用直观的图形找到了数的规律，也用数解决了图形的问题，看来数形结合是一种很好的数学学习方法。

三、数形结合

1. 下面我们一起来做个练习，看看图和数之间有什么规律？（教材P109“练习二十二”，第2题）

2. 照这样的规律，第5个、第6个、第7个能画出来吗？请大家打开书本完成。

3. 如果不画图，想象一下第10个图形是什么样的？有几个点？

四、回顾反思小学阶段关于数形结合的例子

教者通过沟通知识间的内在联系，有意唤醒学生相关活动经验的记忆，沟通与过去学习经验的内在联系，强化了对数形结合思想价值的体现。从这里，我们不难看出所谓的数学思想方法是隐含在数学知识体系里，是无形的，我们只有努力钻研教材，才能挖掘教材中的资源，为渗透数学思想方法做好准备。

二、相机而动，注重时效性

小学生在情境中的注意力是相对分散的，他们更容易关注事物表面的、简单的特征，往往忽视了数学知识内在的本质。每节课仅有40分钟，低年级学生的注意力集中的时间则更短，如何在有限的时间内完成一定的教学任务，实现一定的教学目标，这就要求教师不能只把情境的创设作为课堂教学的摆设和敲门砖。学生虽然可以从情境原型中提出许多问题，这些问题有的却与数学无关，有的不是本节课的教学任务。首先，这就需要教师时刻关注教学动态，及时引导学生进入一个选择与筛选的过程，明晰解决问题的方向；其次，是把能够完成的任务完成好；最后，要让学生迎接挑战——那些目前解决不了的问题怎样才能解决，哪些线索可以利用等，即不在情境中走迷宫，让情境具有更直接的指向性，更好地达成课堂教学目的。

有两位教师对人教版四上“数学广角——优化”例2展开同课异构。A教师提问学生：“谁能说出《田忌赛马》讲的是一个怎样的故事？”然后让一位学生口述这个故事。教师借故事指出“做事情要讲究策略”，进而揭示活动课题。B教师先是出示两组“优中劣”不同等级的马，请学生猜一猜哪一组会胜。有相当一部分学生不知所措，认为是无法确定。接着，教师指出“在同等级的马中甲组更强”，这时全班一致认为是甲组胜。然而教师却否定了结果。为什么呢？这一下便激起了学生的探索欲望。虽然是同一素材，A教师只让学生讲《田忌赛马》故事，更多的像是上语文课，体会不到数学味，既起不到激发趣味，更起不到激起思考、探究欲望的作用。而B教师由故事层层深入，从不知双方马的质量、能力引出“如何使呈劣势的一方获得胜利”的问题。教学中，B教师造成学生的认知冲突，产生疑问，并顺理成章地抛出在“同等级的马中甲组更强”，从而激发学生探究解决的欲望。在这里B教师善于在“趣”与“思”之间寻求结合点，充分发挥情境的潜在功能和教师的主导作用。

三、循序渐进，渗透灵活性

巧解实践性、综合性、条件不定或多余、探索性等不同形式的开放题是数学教学中培养学生发散思维的重要途径。教师要着眼于学生的发展，从学生如何学好的角度出发进行教学素材的整合。同时尽可能把学习的时间和空间留给学生，让他们自己去观察、操作、去发现、去讲解、去总结。

以人教版四上“数学广角——优化”例1的教学为例。课一开始，教师可以设计“今天是妈妈的生日，小明想早起为妈妈准备早餐”的情境——小明起床后要做这几件事：接水1分钟，切面包1分钟，煎蛋5分钟，电水壶烧水8分钟，泡牛奶1分钟，洗水壶1分钟，小明应该怎样安排才能让妈妈尽快吃上早餐？接着，让学生合作探究后来解释自己原先的猜想。在课的最后阶段，又引导学生发现解题中的规律性问题，提出了以下两道思考题：1. 吃完早饭，小明想起还可以帮妈妈做家务，让妈妈轻松一下。他打算做下面几件事：洗碗5分钟，听音乐5分钟，拿衣服去洗1分钟，拖地10分钟，洗衣机洗衣服22分钟，晾衣服5分钟。要做完这些事情，应该怎样安排用时最少？最少需要多长时间？认真对比一下几种方案，你有什么发现？2. 如果洗衣机洗衣服用了15分钟呢？你会如何安排上述事情使用时最少呢？你有没有找到快速解决的方法？

整节课通过设计一系列“起床做早餐”和“做家务”的数学情境串，在教师的层层剖析和学生的自主参与下，学生表现出来的解决策略是多样的。在循序渐进中体会到解决问题策略的灵活性和多样性，也为学生的后续学习做孕伏，承前启后，深浅有度。

关于情境教学的高效践行，实际上取决于教师在课堂引导中的一瞬间，没有情境的教学会让知识枯燥无味，使抽象失去了基石；无法合理凌驾于情境之上的教学便影响了课堂教学的实际效果，造成“捡了芝麻丢了西瓜”的现象。数学教学的真谛是在教学目标的引导下，不断寻找学生学习活动的起点与难点，寻找起点与目标之间的距离及障碍，合理选用教学情境素材，为数学知识的应用找到生长点。再灵活运用教学手段和组织形式，让学生不断地在冲突中经历建构、解构、重构的过程。在学生情境感悟的基础上，对其中所包含的数学知识进行必要的抽象、升华。

（作者单位：福建省福州市鼓楼第一中心小学 本专辑责任编辑：王彬）