引力波、非线性天文学及其应用

张一方

(云南大学 物理系，云南 昆明 650091)



引力波、非线性天文学及其应用

张一方

(云南大学 物理系，云南 昆明 650091)

首先简要介绍了引入引力波及其发现的重要意义.其次讨论天体流体力学和一般的非线性天文学.然后探讨太阳系中的某些具体结果，特别定量讨论小行星形成的混沌模型和太阳黑子的Lorenz模型.进而探讨广义相对论类电磁力的若干力学效应及其在天文学中的应用.最后讨论天体的演化.

天文学，非线性，引力波，流体力学，太阳系，广义相对论

1 引力波及其发现的重要意义

1915年Einstein创立的广义相对论开启了引力理论和宇宙论的新纪元，而且它的某些预言得到了验证.但由此提出的引力波却长期没有得到最后确定，因此引力波的探测和理论一直是相对论和天文学中的研究前沿.1974年美国科学家R.A.Hulse和J.H.Taylor在观测双星系统的过程中，发现一对每个质量都约为太阳质量被定名为PSR1913+6的脉冲双星，并由此提供了引力波存在的间接证据.他们因此获得1993年诺贝尔物理学奖.

2016年2月11日美国科学家D.Reitze宣布第一次直接探测到引力波的存在.引力波被认为是广义相对论实验验证中最后一块缺失的“拼图”，它的发现是物理学界的一个“重大里程碑”.他们利用激光干涉引力波天文台(LIGO)探测到由两个黑洞合并产生的一个时间极短的引力波信号，持续不到1 s.它经过13亿年的漫长旅行，于2015年9月14日抵达地球，被刚改造升级的LIGO的两个探测器以7 ms的时间差先后捕捉到.两个黑洞合并前的质量分别相当于36个和29个太阳质量，合并后的总质量是62个太阳质量，缺失的3个太阳质量的能量以引力波的形式在不到1 s的时间内释放，释放的峰值能量比整个可见宇宙释放的能量还要高出约50倍[1].2016年6月15日LIGO和Virgo的科学家又公布了他们在2015年12月26日再次探测到来自大约14亿光年外两个质量分别为14.2个和7.5个太阳质量的黑洞合并为总质量是20.8个太阳质量的黑洞时发射的引力波[2].毫无疑问，2015-2016年引力波的最终确定是科学上的重大进展，是一个新时代的开端，正如望远镜的发明或太空无线电波的发现一样，由此引力波天文学将成为21世纪的天文学.笔者认为这也将是本年度诺贝尔物理奖的最大热门.

进一步应该探讨引力波的理论问题.值得注意的是，Einstein、Landau、Fock、Weinberg[3-7]等大科学家讨论的都只是一种弱引力场.基于引力场方程的非线性，相应的一般的引力波方程也应该非线性，由此1996年笔者提出引力波应该是非线性波，并且讨论了它的相应的某些特性.特别是引力波速应该和电磁波速不同，起码引力场中光线偏折而引力波速度不会偏折[8].引力波应该具有某些不同于电磁波的特性.对此定量讨论了方程的一些解.引力波的非线性特性来源于引力场的非线性本质[8-10].

早在1981年俄国科学家Ignatev和Balakin就在一个强平面引力波场中得到一个描述等离子体的相对论无碰撞动力学方程的严格解[11].2002年Canfora等分析了一个非Abel Lie代数的真空引力场的不变性，讨论了非线性引力波及其极化[12].2003年Servin等讨论了平面引力波的非线性自相互作用[13].2004年Llberg等考虑在一个磁化等离子体中引力波和电磁波之间的非线性相互作用，由此讨论非线性耦合的Alfvén波和引力波[14].2007年和2010年Aldrovandi等论证了引力波的非线性本质和它们的形式与效应[15,16].2016年Kistovich等还提出稳定非线性引力波的解析模型[17].

新证实的引力波应该是非线性波，不仅因为两个黑洞合并一定是非线性机制，而且释放的巨大能量和持续时间不到1 s的引力波信号必然是脉冲波.进一步的研究也许还可以发现引力波和电磁波之间的不同[8].

2 非线性天文学和天体流体力学

非线性天文学的本质基于广义相对论的引力场方程

(1)

是非线性的.同时各种天体粒子(particles,stars or galaxies)[18]，包括星云、星和星系的流体力学一般也是非线性方程.

天体力学是最早、最经典的理论物理之一[19,20].重子流体方程是：

(2)

重子流体连续性方程在D=0时是

(3)

(4)

重子流体动力学方程是

(5)

(6)

其中ρ是共同运动(comoving)密度，P是压力，E是每单位共动体积的总能，a是膨胀(expansion)参数，Lr,Lc是韧致辐射和Compton冷却(或加热)项，它们一般不重要.系数 Dρk,Dik,DEk引入了人为的(artificial)扩散.由此可以导致天体Schrodinger方程，此时H应该与a有关.Mathews等在密双星系统中用相对论流体力学分析中子星的碰撞[21].

基于星云复杂的流体力学和磁流体动力学，笔者应用非线性方程的定性分析理论得到了双星形成的非线性动力学模型.在一定条件下，二维空间中的一对奇点作为演化结果相应于双星.而在别的条件下，这些方程给出单个奇点，就相应于单星.因此，各种星的形成是星云演化的结果[22-24].其中非线性相互作用和旋转取到非常关键的作用，而线性方程仅仅形成单星[24].这一模型被Steinitz和Farbiash在确定双星中自旋(旋转速度)间的相互关系时称为星云形成的双星张(Zhang’s)非线性模型[25].而且这一方法和模型可以推广和发展.广义相对论是空间大尺度结构任何严格演化理论的基础.笔者计算了广义相对论中普适的2+1维平面的引力场方程，并基于这些方程讨论了星云的演化.对于不同条件，星云可以形成双星或单星.而任何简化的线性理论只能形成单星系统.这证明了非线性相互作用是非常普遍的，所以双星也是十分常见的[26].同时，可以由流体力学方程导出Lorenz方程，而且应用于双星[22,26]，并由二维推广到三维.

天文等中用流体力学方程，在某些条件下只有单变量v.如葛罗米卡方程、Navier-Stokes方程，讨论此时的各种特例；当▽p=0时就只与速度有关.在平面上就可以应用定性分析理论.Navier-Stokes方程及其发展变化的自相似性，可以描述星体演化、分布以及地震[27-29]等，它们都具有自相似性.

由非线性流体力学方程或广义相对论导致极限环和分岔；分岔导致双星、多星系统；极限环导致不同的行星轨道及小行星带、Kuiper带、卫星和土星环等；这又联系于天体从不动点到混沌.小行星带位于类地、类木行星之间，受太阳和大行星共同影响；Kuiper带受太阳影响变小.这是二者的共性.并化为参数，进行定量比较[30].

用流体力学的密度波理论，对焦点，应该导出洛希等势面.

(7)

是等势面.φy=0，a=0，ln(xy)=1或C，也不是椭圆；这应该类似廻旋曲线和卡西尼卵形线

(x2+y2)2-2c2(x2-y2)=a4-c4,

(8)

双纽线

(x2+y2)2=2a2(x2-y2).

(9)

特例，如ln(xy)=0，φy=0，a=0，y2/H=2(x2+y2)，2x2=(H-1-2)y2是两条直线.

更一般，流体力学用于星系的方法可以用于任何流体模型及其方法，直到粒子、碰撞、气象、地震的焦点及风水的聚点等.

3 非线性天体力学

万有引力F=-GmM/r2，结合两体椭圆轨道R=p/(1+cosθ).令GM=k2，p=h2/k2，e=Ap，则

(10)

所以

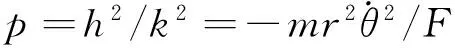
(11)

叠加对应万有引力恒成立.轨道

(12)

迭代或R=r，则

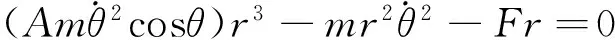
(13)

(14)

(12)代入上述万有引力公式，则

(15)

(16)

方程有4个解.可能对应4个类地、类木行星.如r=an2[31,32]化为8次方程.可能对应8大行星.

非线性天文学包括非线性天体力学[19]，其中有无穷嵌套的自相似结构及小行星、卫星和彗星运动中的混沌性态等.笔者一般地讨论了非线性数学物理中混沌和孤子的推广和应用[33]，及非线性方程孤子-混沌双解的物理意义和泛量子理论等[34].

4 太阳系中的某些具体结果：小行星和太阳黑子

目前小行星起源、演化的主要假设有：1)大行星爆炸说；2)彗星形成说；3)半成品说.我们在此提出混沌-撕裂说：太阳质量占总质量99.8%，距谷神星2.7，但角动量仅占1%；而谷神星距木星2.5；二者距离近似相等.

按照Alfvén太阳系演化的电磁说[35]，在太阳周围形成4个等离子体云，其离太阳的距离由

GMcmi/r=miv2/2=eVi,

(17)

决定，其中Mc是太阳质量.这是引力势转化为动能，动能对应电离能.由此得

2GMc=rv2=a(nv)2,

(18)

即笔者已经得到的v=GM/Hn[31,32].

由此先确定太阳系中太阳至各个行星距离r是Titius-Bode关系或其推广[31,32]相应的唯象方程.大行星的影响力是F+∑Fc.确定方程中的参数及变化范围，何时不变点及环稳定、不稳定，或混沌.r=3.2时是小行星带，对应于混沌.

天体力学中轨道平面的运动方程为[19]：

(19)

其中G和C是积分常数.可得椭圆式.F=k2mM/r2，μ=k2(m+M).不动点

(20)

r4-2Cr2-2μr+G2=0,

(21)

有4个解.

如

(22)

(23)

(24)

由r3-2Cr-2μ=0可以直接得到r的3个解.

小行星相当于太阳系的环，确定其DR.小行星也有Kirkwood空隙，为整数比(1/2，1/3，2/5)及(Hilda 2/3，Trojan 1/1，2/9，3/4)共振行星多，分群族、流型等.这是太阳量子波干涉条纹.

对类地行星及小行星，如果引入参数2.7/3.7=0.73,则距离为r=0.73(0.39,0.72,1,1.52)=0.285,0.526,0.73,1.11，以此为4次方程的4个解的方程：

r4-2.651r3+2.270r2-0.7022r+0.1215=0.

(25)

假设4个r是不动点，或是三角函数或阻尼、反阻尼振动曲线与r的直线方程只有4个交点、解.对Kuiper带可以结合冥王星混沌.以后发展到广义相对论.

小行星带有禁区(Kirkwood环缝)，a=2.50，2.82，2.96，3.28.这可能对应于土星环的缝.用T2=a3标出周期T，则其和木星公转周期11.86年成简单的整数比.而周期比为1/1，4/3，3/2对应的a值，小行星聚集.二者分别对应于限制性三体问题的不稳定或稳定周期解，如KAM理论[36].

196个小行星自转周期的平均值约为10 h，木星是9 h 50 min，土星10 h 14 min，三者近似相等，称为等周律.

太阳黑子的起源目前主要基于上世纪60、70年代发展的湍流发电机理论.已知黑子的纬度分布随时间的变化呈现莫德尔的蝴蝶图；黑子开始于高纬度，以后变到低纬度.应该由太阳流体力学导出对应黑子的Lorenz模型及其方程，

根据图1，可以看出关于混合式教学在中小学领域应用的研究文献最早出现在2007年，并且文献的数量一直在持续增长，原因除了科学发展支撑，还有国家政策引领——在2015年，国务院倡导大众创业万众创新，建立线上和线下、国内与国外、政府和企业合作等一系列的创新机制，越来越多的教育模式应运而生，如创科教育、STEAM教育等[7]。智能机、平板、电脑普及，人人都可以随时随地的使用不同终端进行学习，传统的教学模式得以改变，混合式教学也应运而生，随着科技进步的飞速发展，越来越多的研究者将视角转到了中小学，混合式教学关于中小学应用的研究文献的数量不断增长。

dx/dt=-vx+ky,

(26)

dy/dt=ax-by-xz,

(27)

dz/dt=-cz+xy,

(28)

此时x-y两个量分别相当于纬度和高度或经度.而且二者都基于磁流体动力学方程.

总之，Lorenz方程及其类似方法可以用于天体磁场产生湍流发电机理论.由此产生双中心，可解释太阳活动的蝴蝶图[37,38].较差自转学说能更全面地说明它.此外，黑子蝴蝶图可以作为偶极子.太阳、木星中的电磁场还可能联系于黑子、大红斑.蝴蝶图在空间上是典型的Lorenz混沌蝴蝶，在时间上具有周期性(11年).这从理论基础(磁流体)到观测结果都类似双星[22-24,26].这也联系于太阳黑子数的分形特征.由此也可以解释双星.

可以用粒子团的成团解释宇宙早期物质分布的均匀性演化为目前的不均匀性[39].Arnold在《突变理论》中说：“这解释在数学上等价于对形成的焦散线奇异性(caustic singularity)的分析”.考虑一种无相互作用的介质，即一种非常稀薄的介质.假定粒子间无相互作用，它们在惯性作用下运动，介质的初始速度场，随时间变化.密度也随时间变化.“这样，初始速度场中离开恒定性的小偏离，在足够长时间后会导致粒子堆积的形成(在无穷大密度的地方).当我们从一维介质转向一种充满任意维空间的介质时，以及当我们考虑外部力场或介质产生的场对粒子运动的影响时，甚至当我们需要考虑相对论效应和宇宙膨胀时，上面的结论仍然成立”.

按照天体物理，当宇宙半径比现在小1000倍时，宇宙中物质的大范围分布实际上是均匀的，速度场是有势场.粒子后来的运动导致焦散线的形成，即密度的奇异性和粒子团.在薄饼形成之前，密度一直非常小，可以认为介质无相互作用.

5 广义相对论类电磁力的若干力学效应—及其在天文学中的应用

已知库仑静电场完全类似牛顿万有引力场，而电磁理论是其推广.而广义相对论已经可以导出和电磁理论所有主要公式相似的结果，例如与洛仑兹方程完全相似的公式[4,5]：

(29)

由广义相对论的Einstein和Landau公式可以得到类电磁力.此时，类似于电荷运动产生磁场，物体运动也产生以角速度ω=-(rotu/2c)旋转的类科里奥利力场.通常认为这涉及v/c的高速运动及引力常数k等，所以只对高速，大质量引力场，这些效应才可以测量.

笔者提出只要推广非惯性系和引力场，等价原理就可以普遍成立，而克服其“局域性”.在讨论了非惯性系中加速场或减速场，及引力场或斥力场的关系后，可以得出结论：等价原理在矢量方面等价，但在非矢量方面有所不同.由此提出泛等价原理和泛广义相对论，特别是电磁广义相对论.进而论证了广义相对论的各种实验检验及不足之处，并且讨论了检验电磁广义相对论的某些可能方案[42].

由此可以讨论各种已知和未知的效应，这包括引力波及其推广.这些也是对广义相对论的检验.具体方法是：

1)按照王永久的结果[43]，有de Sitter(1916)进动效应，Kerr度规是匀角速转动球体的外引力场.这应该有相应的类磁场.其中进动效应的角速度是[43]

Ω=am[3r(r·a)-ar2]/r5.

(30)

类似电磁场的4极矩及相应公式[41]：

Ω≅(c/2)rotg=k[R2M-3R(M·R)-]/c2R5.

(31)

这还包括《引力论和宇宙论》第5章的各种引力加速效应[43]：引力、斥力转化，类科氏力和类光学效应中的引力Stark效应、Cerenkov辐射、对应磁场的Seeman效应、Faraday效应.

2)按照电磁理论，讨论磁场、运动变化的电场及一般的电磁场.总之与静电场(相应于万有引力场)不同的各种场.

类似磁场，应该有Biot-Savart定律和拉莫尔定理等.旋转参考系中的科里奥利力

F=2mv×Ω,

(32)

等价于荷电粒子在磁场中所受到的力

(33)

两方面再结合.

这包括Thirring效应及20世纪70年代早期提出的B.Unrub效应，它是根据量子力学和相对论，则任何一个加速运动的物体必被包围在热的光子气中，其温度T=a(h-/2πc).这可以用于行星等的天体运动，联系于随机零点运动、真空量子涨落.进而这可以推广到一般场.如泛相对论c→ch，泛量子论h→H(hi)[31,32]等.

进而与后牛顿力学(parametrized post-Newtonian formalism)和电磁广义相对论[40,41]比较、结合.后牛顿力学可以检验各种度规理论.并且电磁广义相对论可以类似推广到王永久总结的各种效应[43].反之，Kerr场中的某些效应，电磁场及电磁广义相对论中也应该有.

6 天体的演化

布朗运动是混乱的，但当它们彼此之间的相互作用较大时就会凝聚.这完全类似星的形成.实验表明不同颗粒转动时越转动越不均匀.而且快转分离，慢转均匀.颗粒悬浮在液体中，旋转时也会出现颗粒带现象.这可以应用于行星的形成.类地行星(固体)和类木行星(液体)不同，速度也不同.对此迄今无理论解释，可以结合用泛量子理论解释行星、卫星量子化轨道的方法[31,32].

天体主要是多体系统，应是非线性相互作用.但不一定是混沌，例如水星近日点运动.而且天体虽然敏感地依赖于偶然条件，但以后又是决定论的.

广义相对论方程简化后化为极限环的方程，可以确定行星、卫星及环的轨道.稳定极限环对应椭圆星系、恒星、行星及其环的形成；焦点对应螺旋星系、黑洞.稳定焦点更应该对应黑洞，如银河系中心.如果荷电粒子有角动量，按照等离子体箍缩效应就可以形成环.由此可解释行星和卫星的环，它们是分离态，这又可以结合量子论.

由星的混沌吸引子可以导致分形，即太阳-行星类似行星-卫星(卫星环).这可能是早期星云结构.具体研究太阳系和各个行星的a,H间可能存在的定量关系，并由此可以根据观察与理论的偏差来推断天体演化的先后顺序.其中由三维的Lyapunov指数λ1,λ2,λ3=(-,-,-)则是稳定不动点；(-,-,0)是稳定极限环；(-,0.0)是稳定二维环面；(+,0,-)是奇怪吸引子.由此可以定性确定演化.星系演化也可以结合Lyapunov指数，极限环，周期性(对应对称性)，混沌(对应不规则).双核及多核星系可以类比于双星理论[22-24,26].

这是从存在天文学到演化天文学，是从哥白尼、牛顿到康德、拉普拉斯的天文学.天体演化的非线性方程可以是：1)引力方程；2)流体力学方程；3)电磁方程[33]；4)广义相对论方程；5)泛量子力学方程[31,32].6)天文中可以利用Lienard方程，由环形成行星，能量守恒，阻尼为0.7)天体演化用Ashtekar理论可以是广义相对论、量子理论，对后者先研究Dirac场和规范场.其中的一阶方程还可以化简为线性系统.可把动量化为波函数讨论天体演化.

银河系形成于内部坍缩(Eggen-Linden-Sandage模型,1962)或外部吸积-并合(Searle模型,1977).但是，合并模型为主的各种演化机制都存在几率问题.

Athanassoula系统研究了星系的旋涡结构[44].目前认为旋涡星系、不规则星系属于晚型星系；X射线光度范围分别约为1035～1038erg/s；椭圆星系、透镜型星系属于早型星系；X射线光度范围分别约为1039～1042erg/s.前者是两个不同的演化方向，或是越来越散的不同层次.

盘(disk)普遍存在于宇宙中，从银河系、太阳系、双星、黑洞到巨行星的环.在超级计算机上模拟宇宙的演化可以得到一个个星系，这对应引力模拟.A.Linde,A.Vilenkin提出多宇宙.

由定性分析理论得到一些不等式、判别式可以得到1)单星、双星判别式.2)由Lin密度波方程得到星系稳定判别式；并可以推广到广义相对论判别式.3)可以结合星体稳定判别式.

更一般，我们从不可逆物理研究了演化物理，讨论了各种时间箭头并且它们可能统一为统计性时间箭头，探讨了时间不可逆的数学形式，包括半群和矢量的超复数时间，由此数学地提出半群物理和半群科学，进而讨论矢量时空、熵减和不同几何中的不对称性，推广的Noether定理和演化的世界[45].

[1]LIGO.Abbott B P,et al.Observation of gravitational waves from a binary black hole merger[J].Phys.Rev.Lett.,2016,116(6): 061102.

[2]LIGO and Virgo B P,Abbott B P,et al.LIGO bags another black hole merger[J].Phys.Rev.Lett.，2016,116(24): 241103.

[3]爱因斯坦A.爱因斯坦文集(第二卷)[M].范岱年,赵中立,许良英,编译.北京：商务印书馆，1977:367-383.

[4]爱因斯坦 A.相对论的意义[M].李灏,译.北京:科学出版社,1961.

[5]朗道L,栗弗席兹 E.场论[M].任朗,袁炳南,译.北京:人民教育出版社,1959.

[6]福克 V.空间,时间和引力的理论[M].周培源,等译.北京:科学出版社,1965.

[7]温伯格 S.引力论和宇宙论[M].邹振隆,等译.北京:科学出版社,1980.

[8]Chang Yi-Fang.Nonlinear Nature of Gravitational Wave[J].Apeiron,1996,3(2):30-32.

[9]张一方.引力波应该是非线性波[J].吉首大学学报,2009,30(1):153-158.

[10]Chang Yi-Fang.Nonlinear mathematics and general nonlinear sciences[J].International Journal of Modern Mathematical Sciences,2016,14(1):63-76.

[11]Ignatev Y G，Balakin A B.Nonlinear gravitational waves in plasma[J].Russian Physics J,1981,24(7):593-597.

[12]Canfora F，Vilasi G，Vitale P.Nonlinear gravitational waves and their polarization[J].Phys.Lett.B,2002,545(3-4):373-378.

[13]Servin M，Marklund M，Brodin G，et al.Nonlinear self-interaction of plane gravitational waves[J]. Phys.Rev.D.,2003,67(8):875-875.

[14]Llberg A K，Brodin G，Bradley M.Nonlinear coupled Alfvén and gravitational waves[J]. Phys.Rev.D.,2004,70(4):044014.

[15]Aldrovandi R，Pereira J G，Vu KH.The nonlinear essence of gravitational waves[J]. Foundations of Physics,2007,37(10):1503-1517.

[16]Aldrovandi R，Pereira J G，Rocha R D，Vu K H.Nonlinear gravitational waves: their form and effects[J]. International Journal of Theoretical Physics,2010,49(3):549-563.

[17]Kistovich A V，Chashechkin Yu D.Analytical models of stationary nonlinear gravitational waves[J].Water Resources,2016,43(1):86-94.

[18]Longair MS.Galaxy Formation[M].Springer-Verlag,1998.

[19]Brouwer D,Clemence G M.Methods of Celestial Mechanics[M].New York & London: Academic Press,1961.

[20]孙义燧,周济林,现代天体力学导论[M].北京：高等教育出版社,2008.

[21]Mathews G J,Marronetti P,Wilson J R.Relativistic hydrodynamics in close binary systems: Analysis of neutron-star collapse[J].Phys.Rev.,1998,D58(4):043003.1-13.

[22]Zhang Y F (Chang Yi-Fang).A nonlinear dynamical model of formation of binary stars from a nebula[J].Chinese Astron.Astrophys.(UK),2000,24(3):269-274.

[23]张一方,李艳梅.双星形成的非线性动力学机制和定性分析理论[J].云南大学学报,2002,24(2): 104-107.

[24]Chang Yi-Fang.Hydrodynamics and a nonlinear dynamical formation model on binary stars[J].Phys.Scr.,2007,76(4):385-387.

[25]Steinitz R,Farbiash N.Spectroscopically and Spatially Resolving the Components of Close Binary Stars[C].ASP Conference Series.in Dubrovnik,Croatia,2004,Oct.20-24.

[26]Chang Yi-Fang.Lorenz model and plane general relativity model on formulation of binary stars[J].International Journal of Modern Theoretical Physics,2013,2(1):1-12.

[27]张一方.地震的非线性动力学系统的探索[J].大自然探索,1997,16(3):51-55.

[28]Chang Yi-Fang.Nonlinear dynamics and forecasts on earthquake[J].Matter Regularity,2007,7(1):6-12.

[29]Chang Yi-Fang.Nonlinear dynamics,magnitude-period formula and new research on earthquake[J].International Journal of Sciences,2012,Nov.1-9.

[30]Blanco S,Costa A,Rosso O.Chaos in classical cosmology(II)[J].Gen.Rel.Grav.,1995,27(12): 1295-1307.

[31]张一方.Titius-Bode定则的发展,天体量子论和泛量子理论[J].云南大学学报(自然科学版)，1993,15(4): 297-303.

[32]Chang Yi-Fang.Development of the Titius-Bode law and the extensive quantum theory[J].Physics Essays,2002,15(2):133-137.

[33]张一方.非线性数学物理中的混沌、孤子及其新探索[J].商丘师范学院学报，2010,26(9): 57-63.

[34]张一方.非线性方程孤子-混沌双解的物理意义,泛量子理论和非线性数学的某些应用[J].商丘师范学院学报，2011,27(3):46-53.

[35]Alfvén H.On the Origin of the Solar System[M].Oxford Univ.Press,1954.

[36]周济林,孙义燧.行星环动力学[J].天文学进展,1996,2:130-136.

[37]Babcock H W.The topology of the Sun’s magnetic field and the 22-year cycle[J].ApJ.,1961,133(2):572-587.

[38]胡文瑞.宇宙磁流体力学(第10章)[M].北京:科学出版社，1987.

[39]Zeldovich Ya B.Gravitational instability: an approximate theory for large density perturbations[J].AAp.,1970,5(1):84-89.

[40]张一方.电磁场的等价原理和电磁广义相对论[J].Matter Regularity,2003,3(2):75-79.

[41]Chang Yi-Fang.GRT extended for electromagnetic fields: equivalence principle and geometrization[J].Galilean Electrodynamics,2005,16(5):91-96.

[42]张一方.等价原理，泛广义相对论及广义相对论的检验[J].商丘师范学院学报,2007,23(12):58-63;70..

[43]王永久.引力论和宇宙论[M].长沙：湖南师范大学出版社,2004.

[44]Athanassoula E.The spiral structure of galaxies[J].Phys.Reports,1984,114(5-6):319-403.

[45]Chang Yi-Fang.Irreversible physics of evolution,arrows of time and semigroup physics[J].International Journal of Modern Theoretical Physics,2015,4(1):59-77.

[责任编辑：徐明忠]

Gravitational wave,nonlinear astronomy and its applications

CHANG YiFang

(Department of Physics,Yunnan University,Kunming 650091,China)

First,the gravitational wave and its discovered great meaning are introduced briefly.Next,the astronomic hydrodynamics and general nonlinear astronomy are discussed.Third,some concrete results in the solar system are researched.In particular,we discuss quantitatively the chaotic model of formation on asteroids,and the Lorenz model of sunspot.Further,some mechanical effects of similar electromagnetic force in general relativity and their applications in astronomy are searched.Finally,the celestial evolutions are discussed.

astronomy; nonlinearity; gravitational wave; hydrodynamics; solar system; general relativity

2016-06-08；

2016-06-29

国家自然科学基金资助项目(11164033)

张一方(1947—)，男，云南昆明人，云南大学教授，主要从事理论物理的研究.

O320

A

1672-3600(2016)12-0025-07