电动汽车充电站布局优化研究

刘 锴，李 昂，孙小慧

(1.大连理工大学交通运输学院，辽宁大连116024；2.中国城市规划设计研究院，北京100037；3.名古屋大学土木环境工程学院，日本名古屋4848603)

电动汽车充电站布局优化研究

刘 锴1，李 昂2，孙小慧3

(1.大连理工大学交通运输学院，辽宁大连116024；2.中国城市规划设计研究院，北京100037；3.名古屋大学土木环境工程学院，日本名古屋4848603)

快速充电站的布局优化需同时考虑因电动汽车续驶里程短、充电时间长等特性引起的不确定性决策问题以及长期建设过程中的连续性优化问题。由此，建立基于仿真的满足总绕行时间最短的电动汽车充电站动态布局优化模型。考虑建设时序的连续性需求，提出基于逐步优化和比较备选方案服务能力的连续性优化方法。通过实证分析探讨模型的优化布局特征和适用性。结果表明，在案例路网中应用该方法可以得到连续性较好的布局，可为快速充电站分期建设提供规划决策依据。随着充电站数量的增加，布局方案既覆盖了需求产生和通过量最大的几个节点，也缓解了因充电需求大量聚集而选择备选充电站的绕行问题。

交通规划；电动汽车；充电站；仿真优化模型；布局连续性；建设时序

0 引言

为了充分发挥电动汽车在能源、环境等方面对交通系统可持续发展的促进作用，充电基础设施的布局规划和先行建设引起越来越多的重视。同时，充电站建设成本较高而财政预算有限，且充电站网络需要分阶段建设。因此，如何提高充电站空间布局的服务效率和确保建设时序的合理性显得尤为重要。

近年来，包括电动汽车充电站在内的新能源汽车燃料供应站布局优化研究虽已取得很大进展，但既有优化模型大多仅仅考虑了补充燃料需求空间分布给定条件下的布局优化，然而电动汽车续驶里程短、充电时间长的特性不仅加剧了快速充电需求时空分布的不确定性，同时要求出行者对充电时间地点和充电站排队问题做出动态决策。另外，既有研究较少考虑如何应用充电站布局优化模型指导建设时序的安排，通常是根据经验确定最终布局方案的建设时序，难以保证先行建设的充电站不仅在建成时期而且在城市发展远期仍然符合最优布局。

本文在既有研究成果的基础上，分析电动汽车充电站布局影响要素，从出行者充电需求时空分布和充电动态决策过程角度出发，考虑快速充电站建设时序的连续性需求，建立一种基于动态仿真的多目标充电站布局优化模型，并通过案例研究探讨该动态模型的优化布局特征，进而通过比较符合建设时序连续性的多组方案的服务水平，给出最优布局和建设时序方案。

1 充电站布局传统优化模型

快速充电站主要满足电动汽车出行中应急充电或者计划外的充电需求，既有布局优化模型和方法主要包括点需求模型、流量需求模型、多目标优化模型等。

文献[1]于1964年提出了P-Median模型的点需求系列模型，假设燃料需求产生点为居住地或工作地而方便人们的出行需求。此后，研究人员通过改进优化目标和有效算法，缓解了基本模型中对于需求发生地点限定[2]和服务容量无限制[3]的假设。

流量需求系列模型的基础模型是文献[4]于 1990年提出的截流选址模型(Flow Capturing Location Model,FCLM)。文献[5]建立了有限容量续航选址模型，缓解了FCLM模型中对续驶里程和同时服务容量的不合理假设。文献[6]进一步提出考虑服务半径的截流选址模型，假设出行者可在既定路径周围一定服务半径内绕道接受服务，然后再返回至原来的最短行驶路径上。

多目标优化模型的研究建立在点需求和流量需求模型的基础上，主要包括最大覆盖/最短路径问题[7]，以及最低投资/最大覆盖问题[8]。

上述模型均未充分考虑因电动汽车续驶里程短、充电时间长等特性引起的不确定性决策问题以及长期建设过程中的连续性优化问题。

2 充电站布局影响因素

1）电动汽车技术制约。

当前市场上技术较成熟的电动汽车在快速充电模式下充满80%电量约需30 min，充电后支持续驶里程约为100～150 km，导致长距离出行需要多次接受充电服务，电动汽车续驶里程和充电时间受到以电池技术为主的技术制约[9]，其充电需求发生的频率和总量特征对充电站的布局和建设规模提出了要求。

2）充电需求的时空分布。

既有研究均考虑了燃料需求的空间分布对充电站布局的影响，然而还需考虑充电需求的时间约束。由于充电时间较长和充电桩容量有限，导致充电站的同时服务能力有限，加剧了时空分布的不确定性，甚至在一定程度上改变了人们的出行习惯，引起充电需求的变化，因此充电站布局应充分考虑充电需求在时间和空间的双重约束[10]。随着电动汽车占有率的不断变化，其充电需求的空间不均匀性和时空差异可能更加显著。

3）出行者的充电选择行为。

文献[11]指出理解燃料补充行为有助于明确燃料供应站布局结构对新能源汽车推广的促进作用，出行者通常在出行的起点或终点附近加油，其中起点附近更为普遍；加油通常在出行途中顺道完成，较少以加油作为单一的出行目的；出行者对燃料供应站的时间经济性比较敏感。电动汽车较长的充电时间导致其对充电桩的占用时间较长，充电站受用地规模或者功率制约导致其同时服务能力有限，易引起充电时排队等待以及寻找其他可代替充电站的行为。

4）建设时序的连续性需求。

受技术发展的影响，国家制定了分阶段的电动汽车发展战略。一方面充电站建设应充分考虑电动汽车未来的技术发展和市场需求，保障当前阶段建设的充电站可以满足未来电动汽车大规模普及时期的充电需要；另一方面充电站建设需要经历较长的阶段，当前布局优化的充电站在未来应该仍然满足布局最优，符合建设时序的连续性需求，降低不必要的资源浪费。

3 考虑建设时序连续性的充电站布局优化模型

由于电动汽车出行增长过程的空间分布难以模拟，本文着重考察电动汽车出行矩阵分布已知，每辆车的出发时刻符合均匀分布，出发时初始电量为符合正态分布的随机变量条件下，充电站分阶段建设的布局优化问题。

本文在文献[11]提出的时空优化模型的基础上适当简化其布局优化的目标，进行模型假设和构建。兼顾模型建立和求解的现实需要，将复杂的现实条件简约化并提出7项假设：1)充电站和车辆之间信息完全共享并及时更新；2)电量消耗仅与行驶里程呈线性关系，而且平均行驶速度为40 km·h-1；3)每个充电站的充电桩数量固定为12个，当待充电车辆数大于充电桩数量时，车辆需等待或者寻找其他可利用充电站；4)电动汽车出发时刻服从均匀分布；5)电动汽车出发时的剩余电量可支持的行驶里程服从正态分布，且在区间[60 km,100 km]范围内，接受快速充电服务后可行驶里程为100 km；6)电动汽车快速充电所需时间为定值30 min，不考虑剩余电量和车辆类型的影响；7)建设充电站资金预算充足，且各充电站的供电容量没有限制。基于上述充电决策机制，建立以总绕行时间最短为目标的布局优化模型：

式中：m为电动汽车编号；DTm为电动汽车m在单程出行中的绕行时间/min；i为路网节点或充电站点；p为充电站总数量/个。约束条件(2)表示建立的充电站总数为p；约束条件(3)表示所有需充电车辆在出行中至少接受一次充电服务；约束条件(4)表示充电站网络应满足所有车辆的充电需求；约束条件(5)，(6)和(7)赋予决策变量整数限制。目标函数中的DTim主要包含电动汽车的等待时间和因为绕行产生的行驶时间，其中等待时间与充电需求的时空分布以及排队系统的特征有关，采用先到先服务的多服务台单队列排队模型[12]。

考虑到充电站建设时序的连续性需求，分别计算预算约束下充电站数量目标为1，2，…，p时的最优布局，其中p表示满足市场需求的最大数量，即任意有充电需求的车辆无须等待且基本不用绕行即可实现充电活动。然后，逐步判断充电站数量为n时的最优布局是否与n+1时的最优布局一致，如果一致则符合建设时序连续性要求，否则选取若干候选方案比较其服务能力，确定最优布局方案和建设时序。

4 实证分析

本文选取文献[13]提出的具有25个节点的路网。如图1所示，圆圈内的数字表示路网节点的编号，圆圈的大小表示该节点的吸引力权重，路段上的数字表示两节点间的路段长度。根据重力模型计算路网交通需求分布[14]，即利用公式计算高峰小时交通需求矩阵，式中Wi和Wj分别为起讫点的吸引力权重，dij为i和j之间的最短路径长度。基于仿真优化的思想和方法，利用Matlab建立虚拟路网和仿真环境，所有车辆按照上述OD分布随机出发，并随机生成电动汽车在出发时刻剩余电量的可行驶里程，比较可行驶里程与出行起讫点间最短路径往返长度的关系，得出路网在高峰小时的充电需求。

4.1 布局优化结果

当所有车辆充电时间为30 min、各充电站充电桩数量均为12个时，在充电站数量逐渐增加的过程中，最优布局位置的变化情况见表1。建设第1个充电站时的最优位置为节点14，但是平均等待时间高达83.5 min，平均绕行时间约为4.1 min。随着充电站数量的不断增加，平均等待时间和平均绕行时间持续减少。当充电站数量增至2个时，平均等待时间和平均绕行时间均降低75%。当充电站数量增至3时，平均等待时间减少77%，平均绕行时间减少62%。当充电站数量为4时，平均等待时间减少90%，下降至0.485 min，对日常出行来说影响非常小，可以忽略，且此时没有绕行行为，即当前路网的最大充电站需求规模为4个，增加充电站或充电桩数量将导致不必要的资源浪费。

图2展示了不同充电站数量的布局优化结果，表2为不同充电站数量条件下各充电站的服务能力。当充电站数量为2和3时，节点14提供的各项服务需求均大于最优位置组合中的其他节点，表明大多数充电需求的最短行驶路径均经过节点14，易导致在短时间内聚集大量待充电车辆，引起排队等待；如果排队时间较长，部分车辆选择绕行至其他节点接受充电服务。在3个充电站的优化结果中，位于充电需求流量较大路段上的节点23处等待的充电需求显著多于节点8，而绕行的充电需求少于节点8，表明在节点23等待的部分充电需求绕行至节点14和节点8。当充电站数量为4时，充电需求流量较大的节点3和24同样服务了最多的充电需求，节点3绕行的车辆最多但无须等待，节点24处等待的车辆最多但是没有绕行车辆，其原因是节点3和24均存在明显的充电需求短时集中现象，但节点24距离其他充电站较远，而节点3靠近节点8，因此节点24处的车辆几乎均选择了等待，节点3处的部分车辆则可以绕行至节点8，导致位于需求流量较小路段上的节点8服务了大量的充电需求。

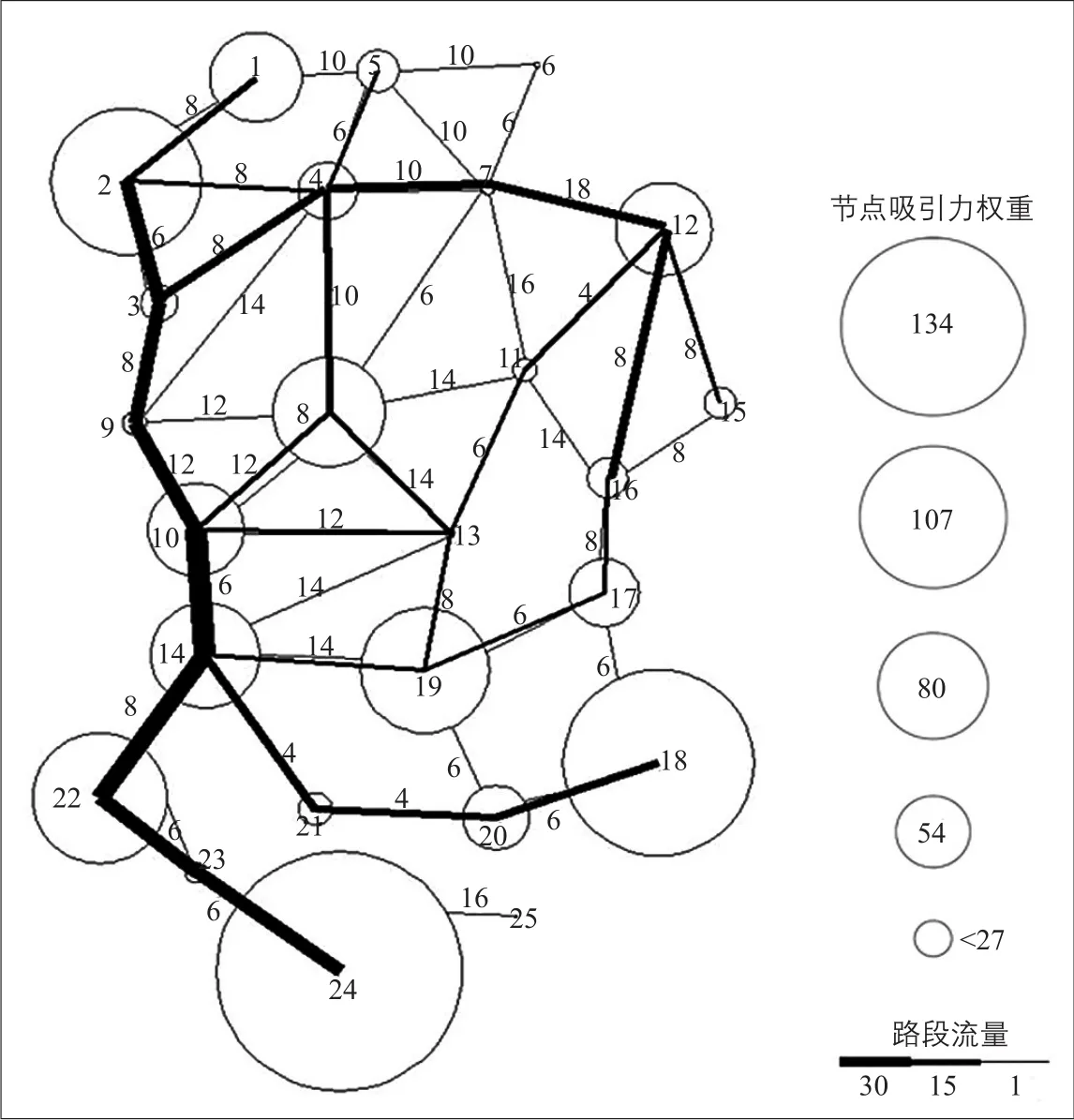
图1 算例路网和最短路径上的充电需求分布Fig.1 Network of case study and the distribution of charging demands on the shortest route

图2 不同充电站数量的布局优化结果Fig.2 Optimized layout schemes under different number of charging stations

4.2 考虑分阶段建设时序连续性的布局优化

当充电站数量从1个增至3个时，其空间布局符合建设时序连续性的需求，但是当增加到4个时，最优布局方案(3,8,12,24)与充电站为3个时的最优布局仅仅有1处相同(节点8)，因此需要进一步比较和优化，以便符合建设时序的连续性需求。4个充电站的布局方案更为分散，覆盖了吸引力权重较大和通过的充电需求流量较多的节点(或邻近节点)，即在出行起点附近为车辆提供充电服务，从而缓解充电需求在网络中心某些节点的短时集聚现象，有效减少了出行中的绕行行为。

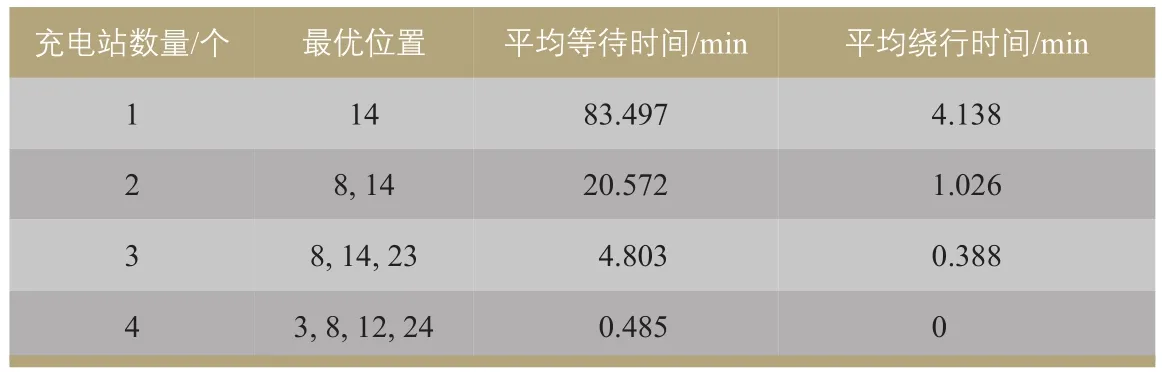
表1 不同充电站数量的优化结果Tab.1 Optimized schemes under different number of charging stations

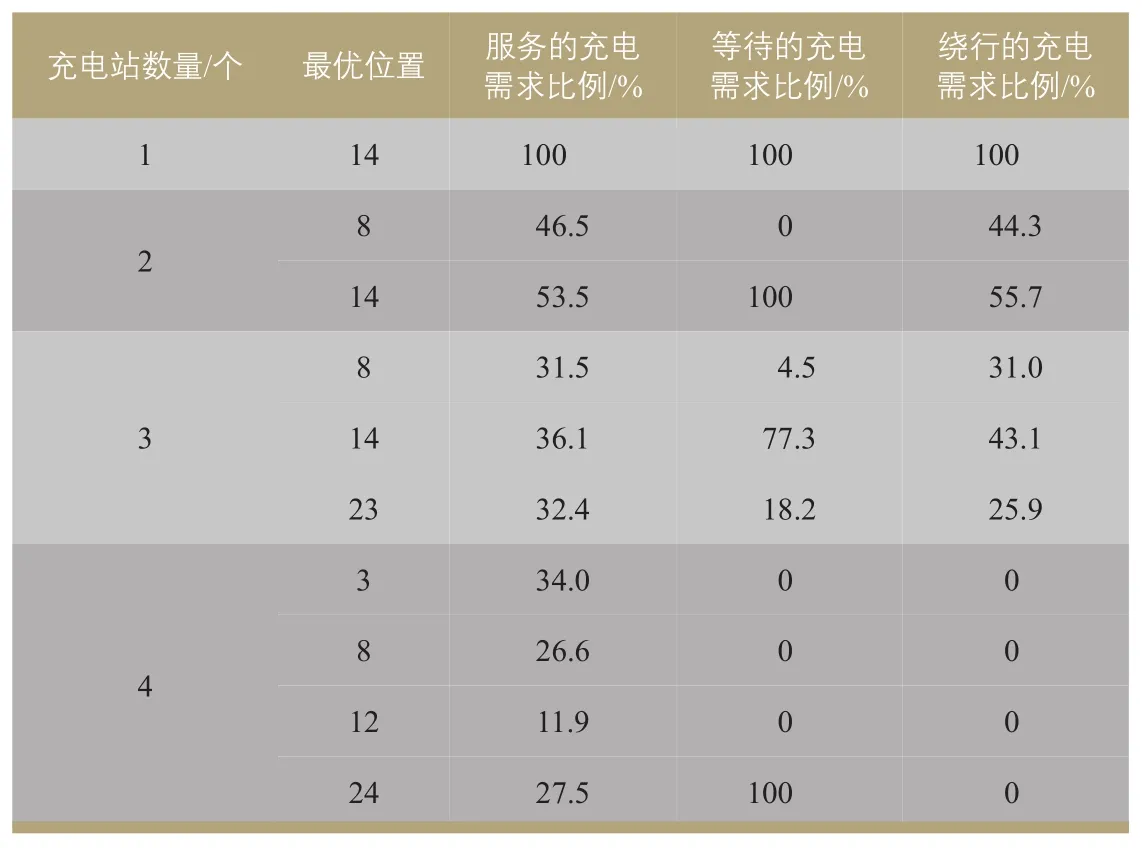
表2 不同充电站数量下各站点服务能力Tab.2 Service capability of each station under different number of charging stations

为了使布局结果满足分阶段连续性的需要，本文对2个满足建设时序连续性的备选方案进行仿真考察。两个方案的服务能力与最优方案的差异见表3。与最优方案相比，两个备选方案均需绕行，但相差较小；备选方案1的平均等待时间显著小于备选方案2，与最优方案基本相同，因此备选方案1略优于备选方案2，且与最优方案的服务能力相差较小。

表3 优化方案比较Tab.3 Comparison of alternative schemes

综上所述，建立在基于个人充电决策规则基础上，以总绕行时间最短为优化目标的布局优化模型可以给出具有较好连续性的优化解，考虑建设时序连续性的多目标比选方法可以进一步修正布局优化方案，此时的建设时序为节点3，8，14，23。节点3，14和23位于需求流量较大的路段上，可以较好满足出行者在出行途中顺道补充燃料的需求；节点8靠近需求流量较大的节点3和14，能够以较短的绕行距离有效分流短时间内聚集的大量充电需求，满足出行者对绕行时间经济性的考虑；同时，节点3和23分别靠近吸引力权重较大的节点2和24，满足出行者在出行起点附近补充燃料的需求。

5 结语

本文在考虑出行充电决策的时空因素对电动汽车充电站布局优化影响的基础上，进一步考虑多个充电站建设时序的连续性需求，通过逐步优化和比较布局方案服务水平，建立同时考虑充电时空分布动态需求和建设时序连续性的电动汽车充电站布局优化模型。该模型在案例路网中的应用研究表明：优化结果有效地拟合了出行者的出行行为，并且较好地适应了电动汽车分阶段发展的需要，对于电动汽车在初期阶段的快速发展具有较好的推动作用，同时还能使初期建设的充电站较好地满足电动汽车大规模普及时期的充电需求。

随着电动汽车的不断普及，今后有必要进一步研究电动汽车实际出行行为特征，并在此基础上构建更加有效的充电决策机制和充电站布局优化方法。此外，模型中对电动汽车出发时刻分布的假设、出发时剩余电量可行驶里程的假设也是今后需要深入研究的问题。

[1]Hakimi S L.Optimal Locations of Switching Centers and the Absolute Centers and Medians of a Graph[J].Operation Research,1964,12 (3):450-459.

[2]Lin Zhenhong,Ogden J,Fan Yueyue,Chen Chien-Wei.The Fuel-Travel-Back Approach to Hydrogen Station Siting[J].International Journal of Hydrogen Energy,2008,33(12): 3096-3101.

[3]Levy J.An Extended Theorem for Location on a Network[J].Operational Research Quarterly, 1967,18(4):433-442.

[4]Hodgson M J.A Flow Capturing Location Allocation Model[J].Geographical Analysis, 1990,22(3):270-279.

[5]Upchurch C,Kuby M,Lim S.A Model for Location of Capacitated Alternative-fuel Stations[J].Geographical Analysis,2009,41(1): 127-148.

[6]杨珺，张敏，陈新.一类带服务半径的服务站截流选址-分配问题[J].系统工程理论与实践，2006(1)：117-122. Yang Jun,Zhang Min,Chen Xin.A Class of the Flow Capturing Location-allocation Model with Service Radius[J].Systems Engineering Theory and Practice,2006,26(1):117-122.

[7]Bapna R,Thakur L S,Nair S K.Infrastructure Development for Conversion to Environmentally Friendly Fuel[J].European Journal of Operational Research,2002,142(3):480-496.

[8]Wang Yingwei,Wang Chuanren.Locating Passenger Vehicle Refueling Stations[J]. Transportation Research Part E,2010,46(5): 791-801.

[9]居勇.建设电动汽车充电站的约束条件及综合效益分析[J].华东电力，2011，39 (4)：547-550. Ju Y.Electric Vehicle Charging Station Constraint Conditions and Comprehensive Benefit Analysis[J].East China Electric Power,2011, 39(4):547-550.

[10]徐凡，俞国勤，顾临峰，张华.电动汽车充电站布局规划浅析[J].华东电力，2009，37 (10)：1678-1682. Xu Fan,Yu Guoqin,Gu Linfeng,Zhang Hua. Tentative Analysis of Layout of Electrical Vehicle Charging Stations[J].East China Electric Power,2009,37(10):1678-1682.

[11]Kitamura R,Sperling D.Refueling Behavior of Automobile Drivers[J].Transportation Research PartA,1987,21(3):235-245.

[12]孙小慧，刘锴，左志.考虑时空间限制的电动汽车充电站布局模型[J].地理科学进展，2012，31(6)：686-692. Sun Xiaohui,Liu Kai,Zuo Zhi.A Spatio-temporal Location Model for Locating Electric Vehicle Charging Stations[J].Progress in Geography,2012,31(6):676-682.

[13]Simchi-Levi D,Berman O.A Heuristic Algorithm for the Traveling Salesman Location Problem on Networks[J].Operation Research,1988,36(3):478-484.

[14]Bersani C,Minciardi R,Sacile R,Trasforini E.Network Planning of Fuelling Service Stations in a Near-term Competitive Scenario of the Hydrogen Economy[J].Socio-Economic Planning Sciences,2009,43(1):55-71.

Optimizing Spatial Distribution of EV Charging Stations

Liu Kai1,LiAng2,Sun Xiaohui3
(1.School of Transportation and Logistics,Dalian University of Technology,Dalian Liaoning 116024,China;2.China Academy of Urban Planning&Design,Beijing 100037,China;3.Department of Civil Engineering,Nagoya University,Nagoya 4648603,Japan)

Determining the distribution of EV charging stations must consider the uncertainties in electric vehicle short driving range and long charging time as well as the long-term sustainable planning for electric vehicle growth.A simulation-based dynamic layout model is developed for minimizing EV searching time for charging station.Considering construction continuity in time and space,this paper proposes a continuous step-by-step optimization method that compares alternative layout plans based on the service capability under different scenarios.The characteristics and applicability of proposed model is discussed through case study.The results show that a high continuity for charging station distribution at network level is achieved with the optimized method,which can help to plan the construction of charge stations in stages.With increasing number of charging stations,the optimized scheme can both cover the nodes with largest charging demands and minimize EV travel time in looking for available charging stations.

transportation planning;electric vehicles;simulation-optimization model;charging stations; continuous distribution;time scheduling of construction

2015-01-01

国家自然科学基金项目“不确定因素下电动汽车需求的行为建模及其对交通系统的影响研究”(51378091)、中央高校基本科研业务费专项资金项目“低排放交通关键技术研究”(DUT12ZD203)、住房和城乡建设部软科学研究项目“城市郊区新城交通体系研究”(2013-K5-32)作者简介：刘锴(1978—)，男，江苏南京人，博士，副教授，主要研究方向：城市交通规划、交通行为建模等。E-mail:liukai@dlut.edu.cn