efficient Orbit Propagation of Orbital Elements Using Modified Chebyshev Picard Iteration Method

efficient Orbit Propagation of Orbital Elements Using Modified Chebyshev Picard Iteration Method

J.L.Read1,A.Bani Younes2and J.L.Junkins3

This paper focuses on propagating perturbed two-body motion using orbital elements combined with a novel integration technique.While previous studies show that Modified Chebyshev Picard Iteration(MCPI)is a powerful tool used to propagate position and velocity,the present results show that using orbital elements to propagate the state vector reduces the number of MCPI iterations and nodes required,which is especially useful for reducing the computation time when including computationally-intensive calculations such as Spherical Harmonic gravity,and it also converges for＞5.5x as many revolutions using a single segment when compared with cartesian propagation.Results for the Classical Orbital Elements and the Modified Equinoctial Orbital Elements(the latter provides singularity-free solutions)show that state propagation using these variables is inherently well-suited to the propagation method chosen.Additional benefits are achieved using a segmentation scheme,while future expansion to the two-point boundary value problem is expected to increase the domain of convergence compared with the cartesian case.MCPI is an iterative numerical method used to solve linear and nonlinear,ordinary differential equations(ODEs).It is a fusion of orthogonal Chebyshev function approximation with Picard iteration that approximates a long-arc trajectory at every iteration.Previous studies have shown that it outperforms the state of the practice numerical integrators of ODEs in a serial computing environment;since MCPI is inherently massively parallelizable,this capability is expected to increase the computational Efficiency of the method presented.

Propagation,Integration,Orbital Mechanics,Classical Orbital Elements,Modified Equinoctial Orbital Elements,Modified Chebyshev Picard Iteration,MCPI,Chebyshev Polynomials,Initial Value Problem,IVP.

1 Modified Chebyshev Picard Iteration

MCPI is an iterative,path approximation method for solving smoothly nonlinear systems of ordinary differential equations.Clenshaw and Norton(1963) first proposed combining the orthogonal Chebyshev polynomials with Picard iteration. Later authors including Shaver,Feagin and Nacozy,and Fukushima further re fined the Chebyshev-Picard framework and also pointed out the parallel computing implications of the method[Shaver(1980);Feagin and Nacozy(1983);Fukushima(1997)].More recent developments in parallelizing MCPI give expected increase in Efficiency[Bai and Junkins(2010);D.Koblick and Shankar(2012);B.Macomber(2015)].

MCPI is a fusion of Picard iteration,which generates a sequence of path approximations,and Chebyshev Polynomials,which are orthogonal and also enable both efficient and accurate function approximation.This method is used to solve both linear and nonlinear,high precision,long-term orbit propagation problems through iteratively finding an orthogonal function approximation for the entire state trajectory.At each iteration,MCPI finds an entire path integral solution(over a large finite interval,converges over intervals up to three orbits using Cowell’s method),as opposed to the conventional,incremental step-by-step solution strategy of more familiar numerical integration strategies,such as those based on explicit numerical methods.significantly,however,unlike conventional integration approaches,it is ideally suited for massive parallel implementations that provide further boosts in the computational performance.Algorithm tests for the present study are currently under development,including massive parallel implementations,where the performance results will be presented in future papers.

In recent years,the research group(Junkins,et.al.)at Texas A&M University has significantly expanded the literature on MCPI.An overview of the the method is given here,while further details may be found in the references[Bai(2010);Bai and Junkins(2011);B.Macomber(2013);Kim and Junkins(2014)].Emile Picard stated that,given an initial conditionx(t0)=x0,any first order differential equation

with an integrable right hand side may be rearranged,without approximation into an integral[Bai and Junkins(2011)]:

For a given suitable starting approximationx0(t),a unique solution to the initial value problem may be found using an iterative sequence of path approximations through Picard iteration as

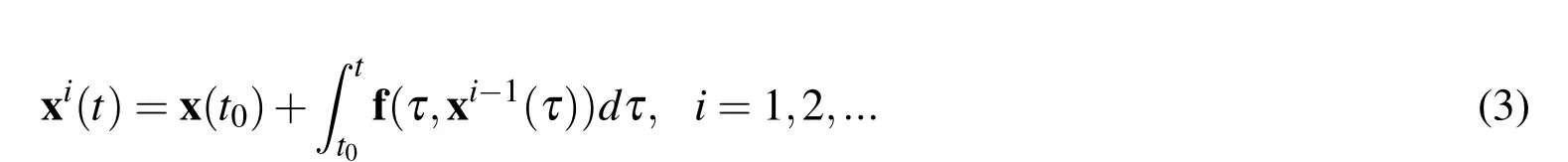
Here,the integrand of the Picard iteration sequence is approximated using Chebyshev polynomials.Because the Cheybshev polynomials are orthogonal,a matrix inverse is not necessary to find the basis function coefficients.Also,the Runge Effect(often seen at trajectory boundaries) is greatly reduced due to a cosine sampling scheme.More details on the basics of the MCPI method may be found in references[Bai(2010)],[Bai and Junkins(2011)],and[D.Kim and Turner(2015)].

Shaver(1980)integrated orbital motion using cartesian coordinates as well as equinoctial orbital elements.He noted that the smooth nature of the element rates makes this set of elements easy to approximate with low-order Chebyshev polynomial series,and that using the Variation of Parameters formulation leads to convergence in significantly fewer iterations.A drag model and low order gravity model were included in these results.Another previous study[Hyun Jo and Choi(2011)]using the J2 gravity term only concluded that using Modified Equinoctial Elements gives a more accurate solution than Classical Orbital Elements.The present study expands Shaver’s results on modern processors and incorporates a high order gravity model to gain insight into the convergence domain and accuracy of using orbital elements.

2 Classical Orbital Elements

Six orbit parameters are used to propagate an orbit;they may be comprised of position and velocity,or alternatively they may be comprised of orbital elements.The classical orbital element set that is used to define the size and shape of an orbit and to propagate perturbed two-body motion ise=(a,e,i,Ω,ω,M0)T,where Ω,i,and ω are the 3-1-3 Euler angle set(longitude of the ascending node,inclination angle,and argument of perigee,respectively)orientating the orbit plane,a is the semimajor axis,e is the eccentricity,and M0is the initial mean anomaly[Schaub and Junkins(2014)].These variables may be easily mapped into Earth-Centered Inertial(ECI)coordinates to obtain acceleration,and vice versa.The position and velocity vectors may be expressed in terms of this set of orbital elements by applying the following direction cosine matrix using a shorthand notation,for instance:andThis rotation matrix is used to orient the orbit plane and line of periapsis with respect to the reference frame.

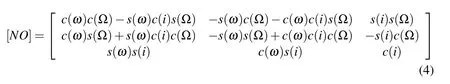
Gauss’Variational Equations may be used to compute the orbital elements as a function of time for a disturbance accelerationadthat is both conservative(i.e.,gravity)and nonconservative(i.e.,drag).The orbital element variations may be integrated by mapping the acceleration vector into the Local Vertical,Local Horizontal(LVLH)frame.Additionally,if the disturbanceadis due to a control thrust,these equations show the resulting effect on the orbit.The variational equations are given in Eq.(5)-(10)[Schaub and Junkins(2014)]in the rotating reference framewhereis in the orbit radial direction,is in the orbit normal direction,andcompletes the orthogonal triad.Here,h is the magnitude of the orbit angular momentum,n is the mean motion,b is the semiminor axis,p is the semilatus rectum,r is the magnitude of the current radius,θ=f+ω,and f is the true anomaly.

Observing these equations indicate the most efficient time in an orbit to make orbital corrections.Note that this orbital element set will be singular for some values,i.e.,when the inclination is zero(i=0,π)and when the orbit is circular(e=0).

3 Modified Equinoctial Orbital Elements

A second set of orbital elements called the Modified Equinoctial Orbital Elements(MEE)is considered;a similar set was used more than a century ago by Lagrange to study secular effects due to planetary perturbations and is well suited for orbits with small eccentricities and inclinations.Broucke and Cefola(1972)showed the original Equinoctial Elements set to be free of singularities for zero eccentricities and both zero and ninety degree inclinations,and they also developed a large number of properties and equations for the set.For the case of retrograde orbits(180°inclinations),the MEE equations are Modified slightly as given by Brouke and Cefola but are still singularity-free.

Brouwer and Clemence(1961)discussed the differential correction orbits with several orbital element sets.The Equinoctial Orbital Elements as defined by Broucke and Cefola are similar to the Set III elements(which are represented by non-integrable differential relations)discussed by Brouwer and Clemence,and they utilize the h and k elements.

The MEEs are a variation of the original Equinoctial Orbital Elements and are defined in terms of the Classical Orbital Elements in Eq.(11)-(16)[M.J.H.Walker and Owens(1985a),M.J.H.Walker and Owens(1985b)].

where p is the semilatus rectum and L is the true longitude.The physical meaning behind these variables is given in D.A.Danielson and Early(Feb 1995).The inverse relationship is

The MEE set utilizes p,the semilatus rectum instead of a,the semimajor axis and also L,the true longitude instead of λ,the mean longitude,in contrast with the original Equinoctial Elements set.One benefit is that p is defined for parabolic orbits.This singularity-free equinoctial formulation utilizes the longitudes λ,F,L instsead of the classical anomalies Mean Anomaly,Eccentric Anomaly,and True Anomaly,M,E,ν respectively[D.A.Danielson and Early(Feb 1995)]:

In this formulation,it is advantageous to write Kepler’s equation in terms of the eccentric longitude F,rather than the eccentric anomaly E,to compute the position vector.This equation and the corresponding radius vector may then be written as

These quantities remain well-defined for the cases of circular or equatorial orbits,eliminating such singular cases known to exist for the Classical Orbital elements.

The radius may alternatively be written as

The transformation to and from Classical Orbital Elements and Modified Equinoctial Elements is easily derived and is given in J.Hyun Jo and Choi(2011).Since the integration of perturbed orbits requires the transformation between orbital elements and ECI in order to compute the perturbing acceleration,the transformation between equinoctial frame and ECI frame(and vice versa)is given in detail by Cefola and Broucke(1975).Analogously to the Classical Orbital Elements case,the three coordinates(x,y,z)may be obtained by premultiplying the coordinates relative to the equinoctial frame by the direction cosine matrix[Broucke and Cefola(1972)]

For this study,Gauss’equations for the variation of the Modified Equinoctial Orbital Elements are the preferred expressions since they are more general than Lagrange’s equations[Roth(1985)].As shown in the results section,these elements increase the domain of convergence over using either cartesian coordinates for Cowell’s method or the Classical Orbital Elements,and they also reduce the number of sample nodes,MCPI iterations,and gravity function calls compared with the cartesian case.The chosen equations are[M.J.H.Walker and Owens(1985a),M.J.H.Walker and Owens(1985b)]

Table 1:LEO(e=0.1)Trajectory Initial Conditions

Table 2:MEO(e=0.3)Trajectory Initial Conditions

4 Simulation

Simulation results are obtained on a Windows 8 machine using Matlab R2013a,where all MCPI results are tuned such that the best performance is achieved while still maintaining a conserved energy(constant Hamiltonian)accurate to machine precision.The initial conditions used for Low-Earth Orbit(LEO)and Medium-Earth Orbit(MEO)are given in Tab.1 and Tab.2;both orbits start at perigee in this case.

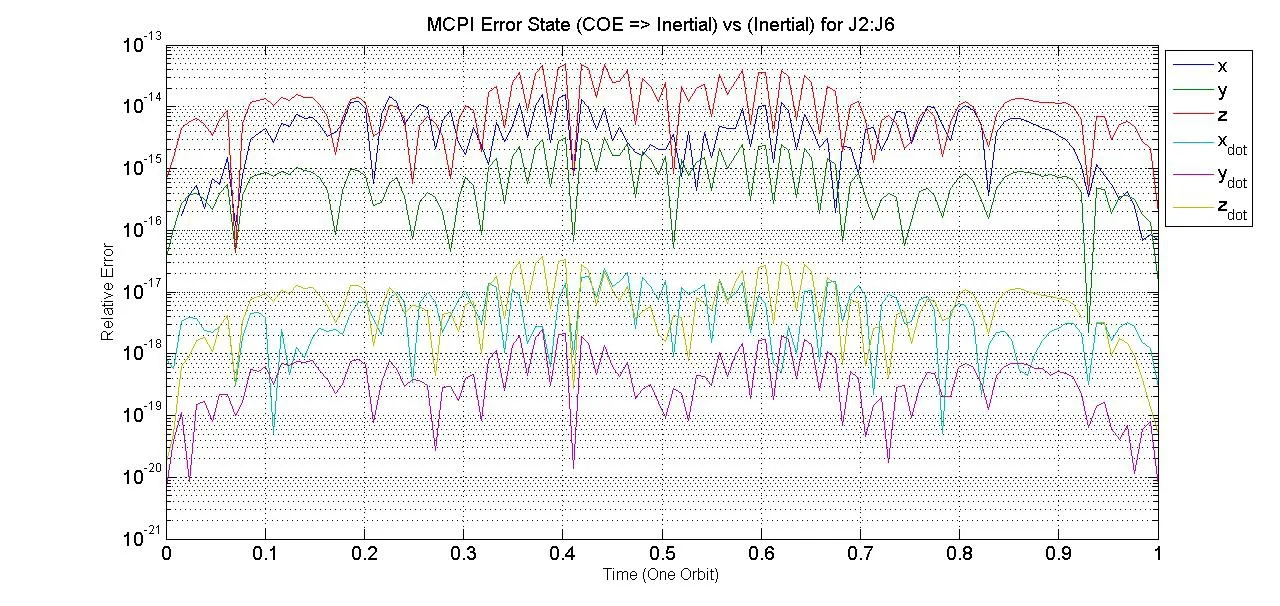
Figure 1:Verification of Classical Orbital Elements Solution vs.Cartesian for One Orbit

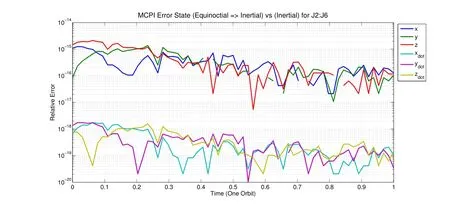
Figure 2:Verification of Modified Equinoctial Orbital Elements Solution vs.Cartesian for One Orbit

Figure 3:Energy Check for Classical Orbital Elements Solution for 13 Orbits(LEO)

Figure 4:Energy Check for Modified Equinoctial Orbital Elements Solution for 53 Orbits(LEO)

4.1 Comparison:MEE vs.Cartesian

LEO results for both the Classical Orbital Elements and the Modified Equinoctial Elements are verified by comparing with a Cowell’s integration method using MCPI,as shown in Fig.1 and Fig.2,as well as spot checked with Gauss Jackson(8th).MCPI using Cowell’s method has been extensively compared and validated against several currently existing methods,including Gauss Jackson(8th),RK1210,RK78,and RK45[B.Macomber(2014)].For the comparision with Cowell’s method,position and velocity are integrated using a perturbed gravity model.Next,the orbital elements are integrated,and then the solutions are converted to position and velocity for this comparison.Cowell’s method requires a different number of sample points(i.e.,for J2:J6,N=100)per orbit than the Orbital Elements cases(i.e.,for J2:J6 gravity terms,N=130 for Classical and N=65 for Equinoctial),so the results are interpolated for this analysis.A smaller number of sample points is needed for convergence using the Orbital Elements cases because MCPI is well-suited to these variables,which vary slowly with time.Once the MCPI coefficients have been computed,the state may be found at any point on the trajectory by using the Chebyshev Polynomials as the basis functions.

One major advantage of using orbital elements is that the solution is convergent for a large number of orbits.For the LEO orbit using J2:J6 zonal accelerations only,the Classical Orbital Elements converges for 12 orbits,as can be seen in Fig.3;the Hamiltonian is conserved until the 13th orbit.The Modified Equinoctial Orbital elements converges for over 50 orbits for J2:J6 before the Hamiltonian check starts to fail,as can be seen in Fig.4.For many applications,only these zonal accelerations are needed to give the desired accuracy;for higher- fidelity applications,a full gravity model must be utilized.

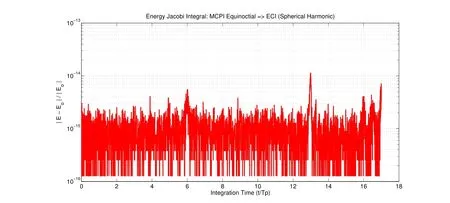
Figure 5:40thDegree and Order Spherical Harmonic Energy Check for Modified Equinoctial Orbital Elements Solution(LEO)for 17 Orbits

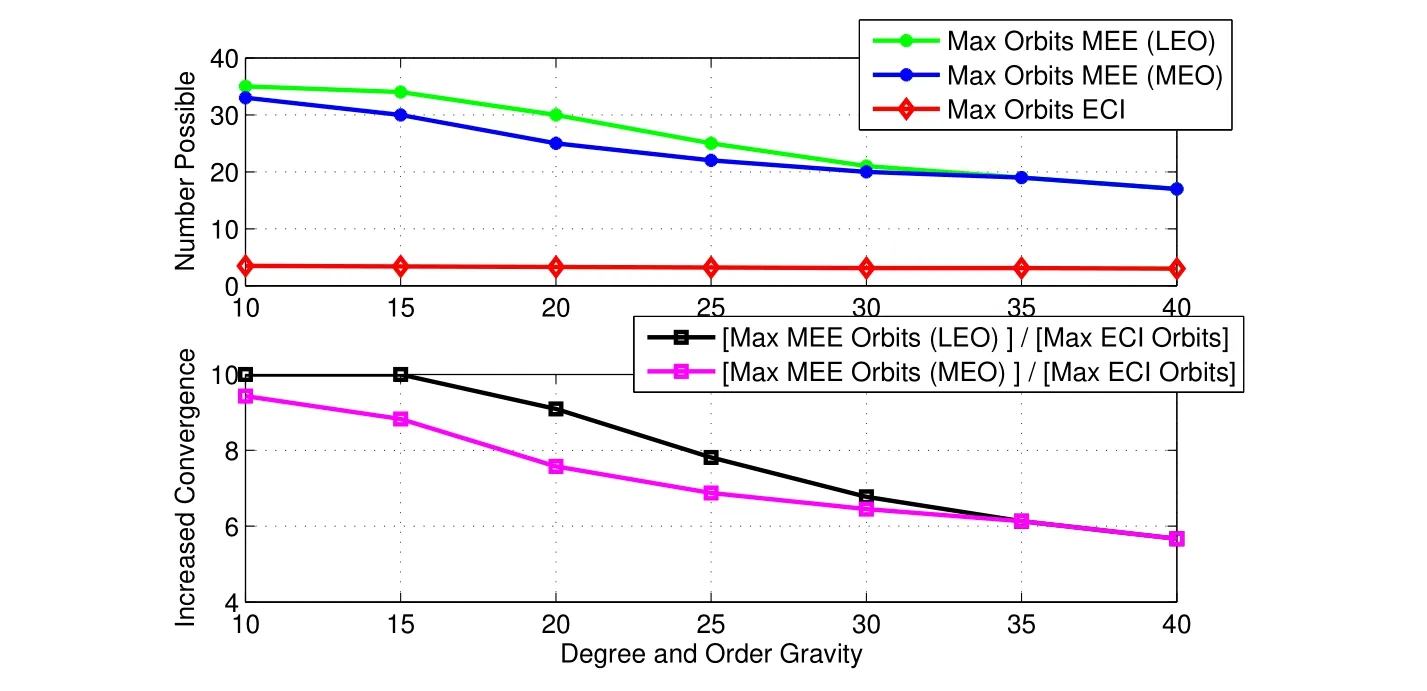
Figure 6:Maximum Number of Orbits Over Which MCPI Will Converge as a Function of Varying Degree and Order Spherical Harmonic Gravity

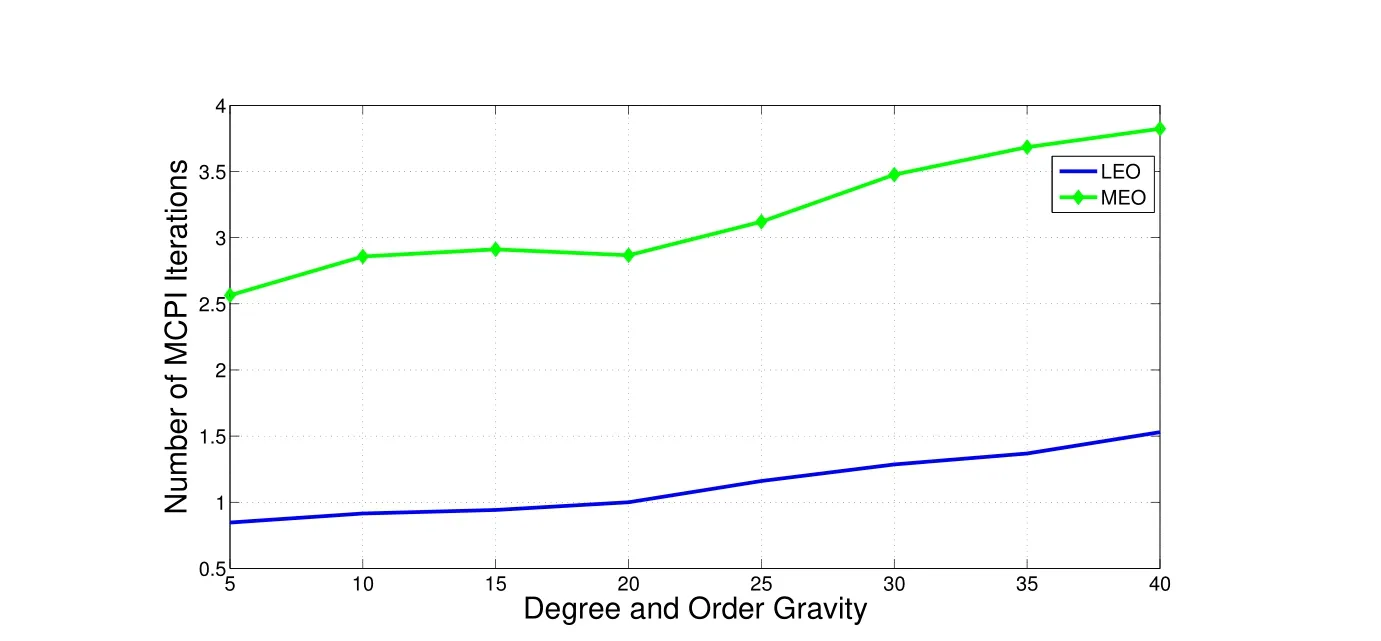
Figure 7:Number of MCPI Iterations Per Orbit as a Function of Varying Degree and Order Spherical Harmonic Gravity

Since the MEEs are the authors’set of choice,a spherical harmonic gravity model is included in the simulation results to provide a more precise solution.The Hamiltonian is conserved for 17 orbits using LEO initial conditions,as is seen in Fig.(5).This number is larger than the maximum number of orbits(up to three)possible using Cowell’s method to propagate position and velocity.The solution is verified against Gauss Jackson(8th)since the energy check over a large number of orbits may not reveal an error in the direction of the velocity.Figures(6)-(8)show the maximum number of orbits for which MCPI will converge,as a function of degree and order gravity,as well as the number of MCPI iterations and number of cosine nodes(sample points)per orbit for both LEO and MEO cases.The present method increases the domain of convergence by＞5.5x compared with using Cowell’s method.These results have been hand-tuned to provide the best solution(i.e.,satis fies hamiltonian conservation)with the fewest number of nodes and largest tolerance possible.However,optimizing the tuning process may provide better results[Macomber and Junkins(2015),Macomber(2015)].

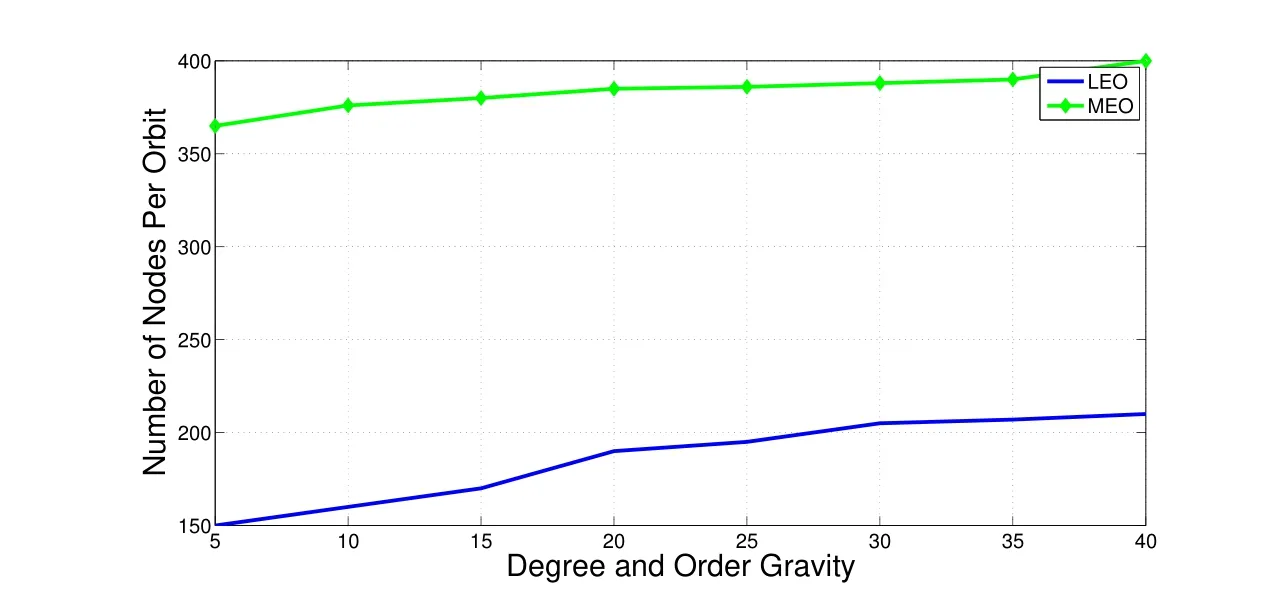
Figure 8:Number of Sample Points Per Orbit as a Function of Varying Degree and Order Spherical Harmonic Gravity

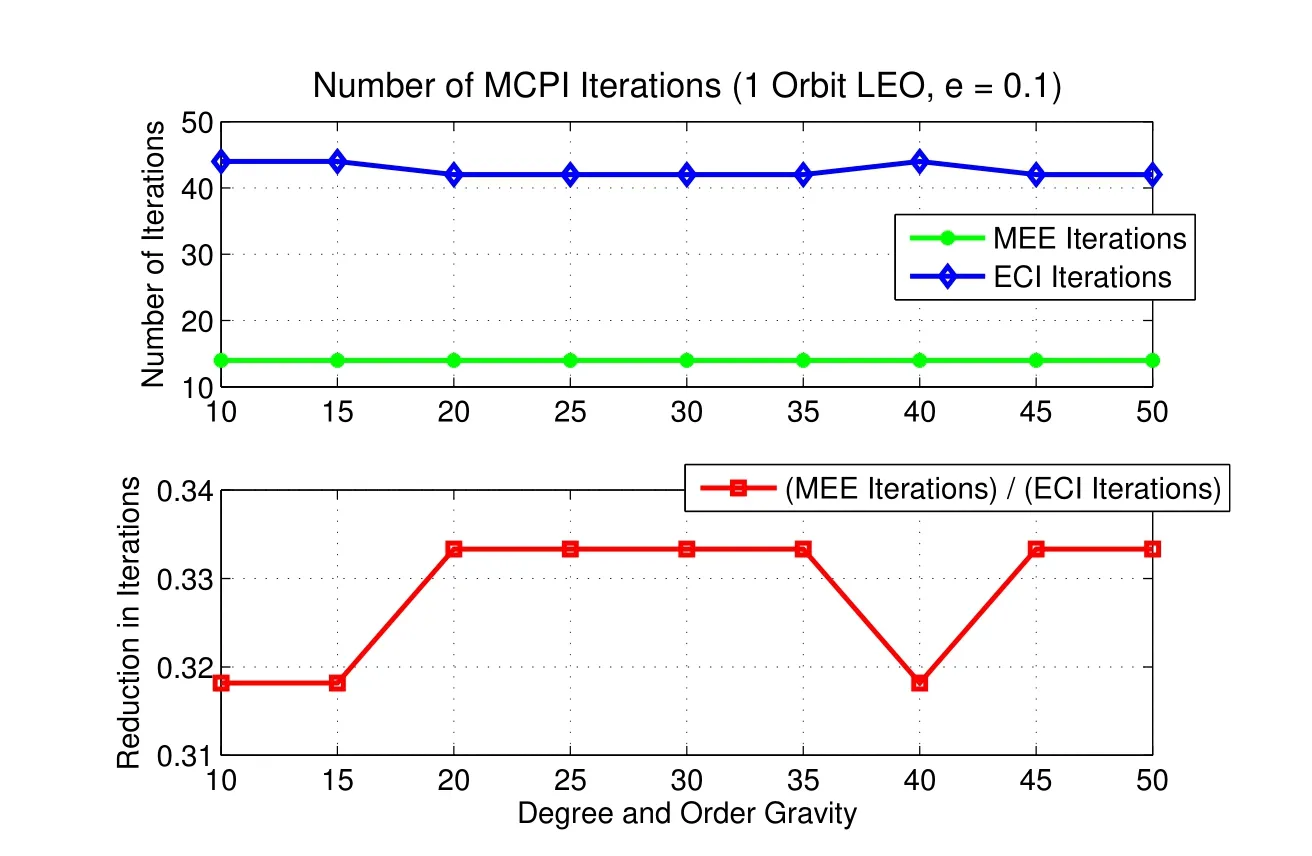
Figure 9:Comparison of MCPI Iterations Per Orbit for MEE versus Cartesian as a Function of Varying Degree and Order Spherical Harmonic Gravity

Figure 10:Comparison of MCPI Gravity Function Calls Per Orbit for MEE versus Cartesian as a Function of Varying Degree and Order Spherical Harmonic Gravity

Figure 11:Segmented Increase in Number of MCPI Iterations Per Orbit as a Function of Varying Degree and Order Spherical Harmonic Gravity

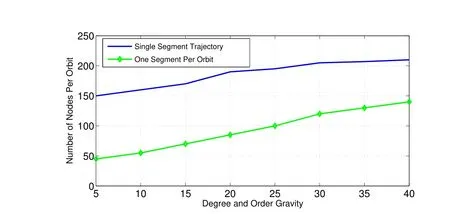
Figure 12:Segmented Decrease in Number of MCPI Nodes Per Orbit as a Function of Varying Degree and Order Spherical Harmonic Gravity

4.2 Segmentation

Previous work[Kim and Junkins(2014),Macomber(2015),D.Kim and Turner(2015)]has shown that segmenting the trajectory increases Efficiency;this method is implemented for the present work as well.Optimal segmentation of Cowell’s method utilizes a fraction of an orbit(typically 1/3 or 1/5 of an orbit per segment).However,since the orbital elements solution converges over a larger number of orbits,a larger segment is used.For this analysis,one orbit per segment is used;in this manner,the final state of the previous segment is used as the initial conditions for the next segment.Similarly to cartesian integration of Earth orbits,segmenting allows for increased Efficiency and decreased number of nodes,even though more MCPI iterations are required.This leads to a reduction in the number of full gravity computations required;since gravity is computationally expensive,initial studies using Matlab show that we achieve a decreased computation time.Figures(11)-(13)show results using a one segment-per-orbit scheme versus using a single segment over the entire trajectory.

Figure 13:Segmented Decrease in Number of Gravity Function Calls Per Orbit as a Function of Varying Degree and Order Spherical Harmonic Gravity

5 Conclusion

Propagation of either the Classical or the Modified Equinoctial Elements is an attractive method to solving the perturbed two-body problem using Modified Cheby-shev Picard Iteration.Both differential equations result in MCPI convergence for a large number of orbits,while Cowell’s method used in conjunction with Modified Chebyshev Picard Iteration only converges for a few orbits in cartesian coordinates,using a single segment.The Modified Equinoctial Elements avoid singularities that are problematic for the Classical Orbital Elements and give a slightly more accurate solution,so they are the preferred choice of variables.Higher order gravity models(such as the spherical harmonic gravity implemented here)lead to analogously long intervals for convergence,albeit with an increase in the number of basis functions.The combination of the Modified Equinoctial Orbital Elements with MCPI leads to decreased number of nodes,MCPI iterations,and gravity function calls when compared with Cowell’s method,which is typically the standard method used in orbit propagation.An initial study using Matlab shows a resulting decrease in computation time for higher degree and order gravity using this segmentation scheme,and the algorithm is currently under development in C++.Optimizing the algorithm by using a segmentation scheme decreases the number of nodes and gravity function calls,at the cost of adding a few more MCPI iterations,to reduce the overall computation time.Further work incorporating the MEEs and MCPI for the two-point boundary value problem is expected to give an increased domain of convergence compared with the cartesian case.In addition,parallelizing this method is expected to further increase the Efficiency since MCPI is inherently well-suited for massive parallel computing.

Acknowledgement:We thank our sponsors:AFOSR(Julie Moses),AFRL(Alok Das,et al),and Applied Defense Solutions(Matt Wilkins)for their support and collaboration under various contracts and grants.Thank you also to Dr.Bob Gottlieb and Dr.Terry Feagin for their collaboration and advice.

B.Macomber,e.a.(2013): Modified Chebyshev Picard Iteration for efficient Numerical Integration of Ordinary Differential Equations.Proceedings of 2013 AAS/AIAA GNC Conference,Breckenridge,CO.

B.Macomber,A.Probe,e.a.(2015):Parallel Modified-Chebyshev Picard Iteration for Orbit Catalog Propagation and Monte Carlo Analysis.Proceedings of the 38th Annual AAS/AIAA Guidance and Control Conference,Breckenridge,CO.

B.Macomber,D.Kim,R.W.J.J.(2014): Terminal Convergence Approximation Modified Chebyshev Picard Iteration for efficient Numerical Integration of Orbital Trajectories.Proceedings of Advanced Maui Optical and Space Surveilliance Technologies Conference,Maui,HI.

Bai,X.(2010):Modified chebyshev-picard iteration methods for solution of initial value and boundary value problems.PhD Dissertation.

Bai,X.;Junkins,J.(2010): Solving Initial Value Problems by the Picard-Chebyshev Method with Nvidia GPUs.Proceedings of the 20th Space flight Mechanics Meeting,San Diego,CA,vol.AAS 10-197.

Bai,X.;Junkins,J.(2011): Modified Chebyshev-Picard Iteration Methods for Orbit Propagation.Journal of the Astronautical Sciences,vol.4,pp.583–613.

Broucke,R.;Cefola,P.(1972): On the Equinoctial Orbit Elements.Celestial Mechanics,vol.5(3):303-310.

Brouwer,D.;Clemence,G.(1961):Methods of Celestial Mechanics.Academic Press.

Cefola,P.;Broucke,R.(1975):On the Formulation of the Gravitational Potential in Terms of Equinoctial Variables.AIAA 13th Aerospace Sciences Meeting.

Clenshaw,C.;Norton,H.(1963):The solution of nonlinear ordinary differential equations in chebyshev series.The Computer Journal,vol.6,pp.88–92.

D.A.Danielson,C.P.Sagovac,B.N.;Early,L.(Feb 1995): Semianalytic Satellite Theory.Mathematics Department,Naval Postgraduate School Report.Monterey,CA.

D.Kim,J.J.;Turner,J.(2015):Multisegment Scheme Applications to Modified Chebyshev Picard Iteration Method for Highly Elliptical Orbits. Mathematical Problems in Engineering,pp.1–7.

D.Koblick,M.P.;Shankar,P.(2012):Parallel high-precision orbit propagation using the Modified picard-chebyshev method. ASME International Mechanical Engineering Congress and Exposition,pp.587–605.

Feagin,T.;Nacozy,P.(1983): Formulation and Evaluation of Parallel Algorithms for the Orbit Determination Problem.Celestial Mechanics and Dynamical Astronomy,vol.29,pp.107–115.

Fukushima,T.(1997):Vector Integration of Dynamical Motions by the Picard-Chebyshev Method.The Astronomical Journal,vol.113,pp.2325–2328.

Hyun Jo,J.,K.P.I.C.N.;Choi,M.(2011):The Comparison of the Classical Keplerian Orbit Elements,Non-Singular Orbital Elements(Equinoctial Elements),and the Cartesian State Variables in Lagrange Planetary Equations with J2 Perturbation:Part 1.Journal of Astronomy and Space Sciences.

J.Hyun Jo,I.Kwan Park,N.C.;Choi,M.(2011): The Comparison of the Classical Keplerian Orbit Elements,Non-Singular Orbital Elements(Equinoctial Elements),and the Cartesian State Variables in Lagrange Planetary Equations with J2 Perturbation:Part 1.Journal of Astronautical Space Sciences,vol.28(1),pp.37–54.

Kim,D.;Junkins,J.(2014): Multi-Segment Adaptive Modified Chebyshev Picard Iteration Method.Proceedings of 2014 AAS/AIAA Space Flight Mechanics Conference,Santa Fe,NM.

Macomber,B.(2015): Enhancements to Chebyshev-Picard Iteration Efficiency for Generally Perturbed Orbits and Constrained Dynamical Systems.PhD Dissertation.

Macomber,B,P.A.W.R.;Junkins,J.(2015): Automated Tuning Parameter Selection for Orbit Propagation with Modified Chebyshev Picard Iteration.Proceedings of 25th AAS/AIAA Space Flight Mechanics Meeting,Williamsburg,VA.

M.J.H.Walker,B.I.;Owens,J.(1985): A Set of Modified Equinoctial Orbit Elements.Celestial Mechanics,vol.36(4),pp.409–419.

M.J.H.Walker,B.I.;Owens,J.(1985):ERRATA:A Set of Modified Equinoctial Orbit Elements.Celestial Mechanics,vol.36(4),pp.409–419.

Roth,E.(1985):The Gaussian Form of the Variation-of-Parameter Equations Formulated in Equinoctial Elements-Applications:Airdrag and Radiation Pressure.Acta Astronautica,vol.12,pp.719–730.

Schaub,H.;Junkins,J.(2014): Analytical Mechanics of Space Systems.AIAA Education Series.

Shaver,J.(1980): Formulation and Evaluation of Parallel Algorithms for the Orbit Determination Problem.PhD Thesis.

1Graduate Research Assistant,Texas A&M University,College Station,TX,USA.

2Assistant Professor,Khalifa University,Abu Dhabi,UAE.

3Distinguished Professor,Texas A&M University,College Station,TX,USA.