Enhancements to Modified Chebyshev-Picard Iteration Efficiency for Perturbed Orbit Propagation

B.Macomber,A.B.Probe,R.Woollands,J.Readand J.L.Junkins

Enhancements to Modified Chebyshev-Picard Iteration Efficiency for Perturbed Orbit Propagation

B.Macomber1,A.B.Probe1,R.Woollands1,J.Read1and J.L.Junkins1

Modified Chebyshev Picard Iteration is an iterative numerical method for solving linear or non-linear ordinary differential equations.In a serial computational environment the method has been shown to compete with,or outperform,current state of practice numerical integrators.This paper presents several improvements to the basic method, designed to further increase the computational efficiency of solving the equations of perturbed orbit propagation.

Astrodynamics,Orbit Propagation,Cheybshev Polynomials,Picard Iteration.

1 Introduction

1.1 Background

Modified Chebyshev Picard Iteration(MCPI)combines the discoveries of two great mathematicians:Emile Picard(Picard iteration)and Rafnuty Chebyshev(Chebyshev polynomials for orthogonal approximation).The decision to make use of orthogonal Chebyshev function approximation and Picard iteration in a simultaneous manner for solving non-linear Ordinary Differential Equations(ODEs)was first proposed in[Clenshaw and Norton(1963)].Later authors further re fined the Chebyshev-Picard framework,and the parallel computing implications of the method[Shaver(1980);Feagin and Nacozy(1983);Fukushima(1997)].Bai’s dissertation extended the earlier MCPI works and proved the capability of the method to compete with,or outperform,the state of the practice for numerical integration of ODEs[Bai(2012)].Bai and Junkins applied MCPI to non-linear Initial Value Problems(IVPs)and orbit propagation[Bai and Junkins(2011a)],and showed that MCPI can outperform other higher order integrators such as Runge-Kutta-Nystrom 12(10)[Bai and Junkins(2011c)].Bai and Junkins have also demonstrated using variations of MCPI to:(i)efficiently solve Lambert’s transfer problem,(ii)solve anoptimal control trajectory design problem more accurately and efficiently than the Chebyshev pseudospectral method[Bai and Junkins(2011b)],(iii)and to evaluate complex three-body station-keeping control problems formulated as a Boundary Value Problem(BVP)[Bai and Junkins(2012)].In 2013,Bani-Younes’dissertation expanded upon the benefits of MCPI,and orthogonal approximation as a whole,for perturbed orbit propagation[Bani-Younes(2013)].More recently,Macomber’s dissertation presented a body of work to enhance the overall performance and algorithmic automation of MCPI[Macomber(2015)].

In the above developments,MCPI in a serial environment has been shown to be able to compete with,or outperform,the state of the art numerical integration algorithms for solution of a variety of initial and two point boundary value problems.MCPI has the added benefit that it is an inherently massively parallelizable method,a claim that is not possible for other competing algorithms except for a subset of Implicit Runge-Kutta algorithms.Massively parallel MCPI has been shown capable of orders of magnitude performance increase over serial implementations for a variety of orbit propagation problems[Shaver(1980);Koblick,Poole,and Shankar(2012);Woollands,Read,Macomber,Probe,Bani-Younes,and Junkins(2015);Bai and Junkins(2011a,2010);Macomber,Probe,Woollands,and Junkins(2015a)].However,tuning of MCPI(time segment lengths and degree of Chebyshev approximation)is problem-dependent.A tuning study must frequently precede the realization of the advantages discussed above[Macomber,Probe,Woollands,and Junkins(2015b)].As shown in[Macomber(2015)],while MCPI can converge over multiple orbits for low eccentricity cases,optimal Efficiency is obtained for several segments per obit(typically three to five).For the Molniya orbit,seven segments are rquired for optimal Efficiency.

This paper presents a set of improvements to basic MCPI(as presented in the above references),for increasing the computational performance of perturbed orbit propagation.Numerically propagating high- fidelity orbits requires evaluation of computationally expensive perturbation force models,and generally these force function evaluations account for the vast majority of computation time.The spherical harmonic gravity series is one of the most costly of these models to calculate if high precision solutions are required.Because MCPI is an iterative method,and the force functions must be evaluated on every iteration,there are two strategies for reducing total computation time.The first is to decrease the computational cost per iteration,and the second is to decrease the number of iterations.In Sec.2.1,an adaptive spherical harmonic gravity method is presented that automatically chooses the necessary spherical harmonic series degree and order based upon the required acceleration precision and the instantaneous orbital radius.For highly eccentric orbits,the number of terms in the gravity expansion may vary from tens of thousands near perigee to fewer than 50 terms near apogee,without accuracy loss.Similar studies not relating to MCPI have been previously conducted by other authors,for instance[Arora and Russell(2015)].In Sec.2.2,a Taylor series method is presented for approximating high- fidelity gravity accelerations using computationally cheaper lower- fidelity function evaluations,either between subsequent Picard iterations,or for neighboring trajectories in the vicinity of a reference trajectory.Due to the fixed point nature of Picard iteration convergence,the later iterations approaching final convergence result in multiple gravity force evaluations very near fixed points in the force field.The small spatial variations of gravity near each node can be captured with very efficient local models.Sec.2.3 presents a method for improving the initial state estimate at each function evaluation point,thus reducing the required number of Picard iterations.

1.2 MCPI Fundamentals

An Ordinary Differential Equation(ODE)

with a state vector xxx (t)∈Rn,and a given initial condition xxx000at initial time t0,may be rearranged without approximation to obtain the integral equation

Picard proved that a sequence of approximate solutions of increasing accuracy xxxi(t),i=1,2,3,...to this integral formulation may be recursively generated by

Picard’s Method of Successive Approximations,now called Picard iteration,constitutes a contraction mapping to the true solution xxx(t)under broadly applicable assumptions[Picard(1893)].For any smooth,integrable,single-valued function fff(t, xxx(t)),the sequence converges over some interval(tf−t0)＜δ for all starting xxx0(t)within the range|| xxx0(t)− xxx(t)||＜ ∆,where δ and ∆ are finite and can be roughly bounded.The rate of convergence is largely dictated byandand is approximately a geometric sequence.

In the MCPI method,orthogonal Chebyshev polynomials[Chebyshev(1857)]are used as a basis set to approximate the integrand in the Picard integral of Eq.3.Chebyshev polynomials reside in the domain τ=[−1,1],and can be generated recursively as:

Derivatives and integrals of the Chebyshev polynomials are defined analytically in terms of the polynomials themselves,which allows analytic integration of the integrand function within Picard iteration.Therefore all derived state variable approximations are easily,and kinematically consistently,represented as a Chebyshev series.The integration property of Chebyshev polynomials states that

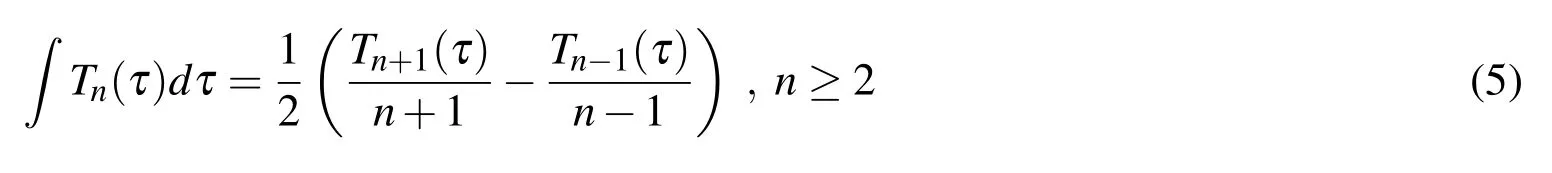
Unlike traditional step-by-step integrators,during implementation of MCPI long state trajectory arcs are approximated at each Picard iteration.The independent variable in the system dynamics is scaled and shifted such that the timespan of integration is projected onto the domain(−1≤τ≤1)of the Chebyshev polynomials,thus the system states can be approximated using the Chebyshev polynomial basis functions.The orthogonal nature of the basis functions means that the linearly scaled coefficients may be computed independently as simple ratios of inner products,with no matrix inversion.

A key feature of MCPI is the utilization of time nodes corresponding to a nonuniform cosine density sampling of the domain of the Chebyshev basis functions,called Chebyshev-Gauss-Lobatto(CGL)nodes:

This sampling scheme is chosen to exploit the discrete orthogonality property of the Chebyshev polynomials of the First Kind.In contrast to the nodes for discrete orthogonality of Legendre polynomials,no iteration of a transcendental equation is required to compute these nodes.The CGL sampling has much higher density towards the edges of the±1 domain than in the center.This provides,for most approximation problems,a near-uniform approximation error in spite of the lack of support to the left of τ= −1 and to the right of τ=+1.Of vital importance,the sampling scheme greatly reduces the Runge phenomena,a common issue in function approximation whereby large approximation errors are created near the segment boundaries due to lack of knowledge of the states outside the boundaries.It can be shown,as a practical matter,that the approximation error amplitudes are much more nearly constant as a consequence of cosine sampling,in comparison to uniform sampling.Furthermore,sampling consistent with the discrete orthogonality conditions of the Chebyshev polynomials(or any other orthogonal polynomial basis functions)eliminates the necessity of a matrix inverse and enables machine precision approximation of the integrand in Picard iteration[Junkins,Bani-Younes,Woollands,and Bai(2012)].

Note that any orthogonal polynomial basis function set gives rise to an algorithm analogous to MCPI.However,the Chebyshev polynomials have some advantages:(i)the cosine clustering of denser nodes (in order to leverage discrete orthogonality)results in very small Runge effect(large approximation errors near the ends of the interval)compared to other sampling schemes,and(ii)the nodes for discrete orthogonality are algebraically computed with no need for iteration.Experiments show that the Chebyshev polynomial basis set is slightly preferred over Legendre polynomials for implementation with Picard iteration[Junkins and Bai(2012)].

1.3 Second Order MCPI

Consider a second order Ordinary Differential Equation

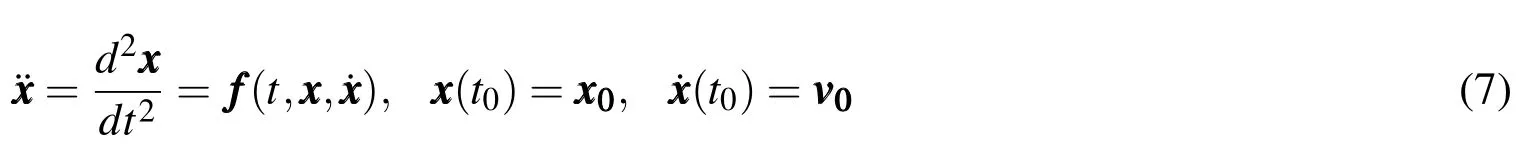
In this section,an outline is presented of yet one more variation of the MCPI cascade method for second order ODE systems.This new method rigorously enforces the kinematic relationship between the acceleration,velocity,and position state Chebyshev coefficients using the analytic integration property of the Chebyshev polynomials,and avoids truncating certain small terms in the Chebyshev series as in the previous developments[Bai(2012);Bani-Younes(2013)].An explicit term-by-term derivation of the core equations and the vector/matrix formulation is rigorously derived in[Macomber(2015)].

In order to satisfy the second order ODE,the kinematic relationships

must be true at all times.The independent time variable is shifted and scaled from t0≤t≤tfto a new variable−1≤τ≤1 by the transformation

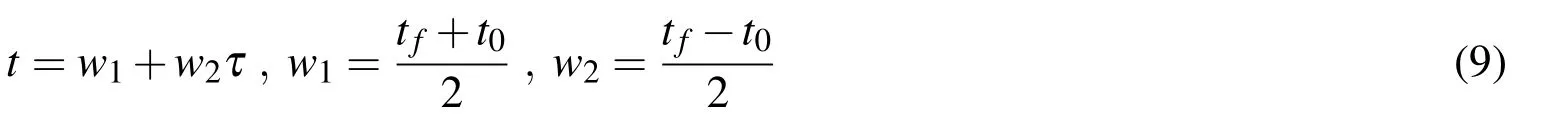
Similarly scaling the dynamics defined by the ODE,the transformed kinematic relationships,written as

must be true at all times.Rearranging the above differential equations to integral equations may be performed without approximation.Picard updates to the velocity states are obtained by

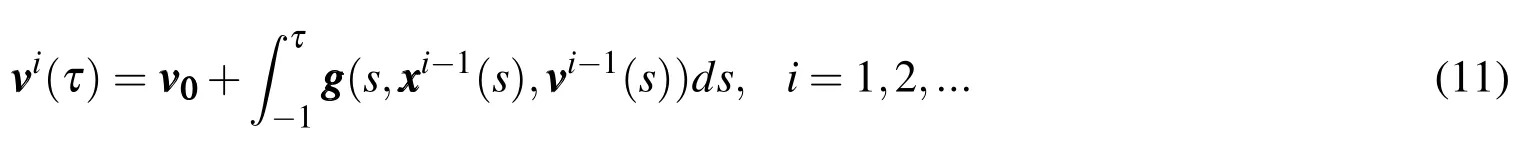
and kinematic updates to the position states are obtained by

Notice that Eq.12 is not Picard iteration,it is simply an integral of an exact kinematic constraint between vvvi(τ)and xxxi(τ).Whereas the integrand of the Picard iteration of Eq.11 contains the position and velocity state history along the(i−1)thtrajectory approximation,Eq.12 is simply the integral of the ithvelocity history to obtain the ithposition history.

Orthogonal function approximation with Chebyshev polynomials may be accomplished with either of two very closely related formulations:the interpolation approximation,or the least squares approximation.Both methods are valid when sampling the function at the Chebyshev-Gauss-Lobatto(CGL)nodes of Eq.(6).

When the number of CGL sample points M is equal to the Chebyshev order of approximation N,the interpolation method is used.When more CGL sample points than the Chebyshev order of approximation are used(M＞N),the least squares method is used.[Fox and Parker(1968);Macomber(2015)].Using the interpolation approximation formulation,an Nth-order Chebyshev polynomial sequence is used to approximate the ithPicard estimate of the system position states sampled at M=N CGL nodes

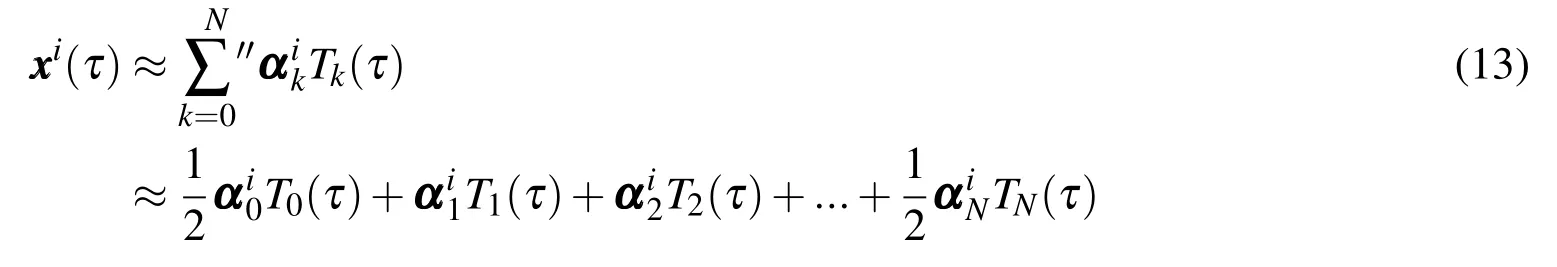
The velocity states are approximated with an(N−1)th-order Chebyshev series,again sampled at M=N CGL nodes,using the least squares Chebyshev approximation formulation

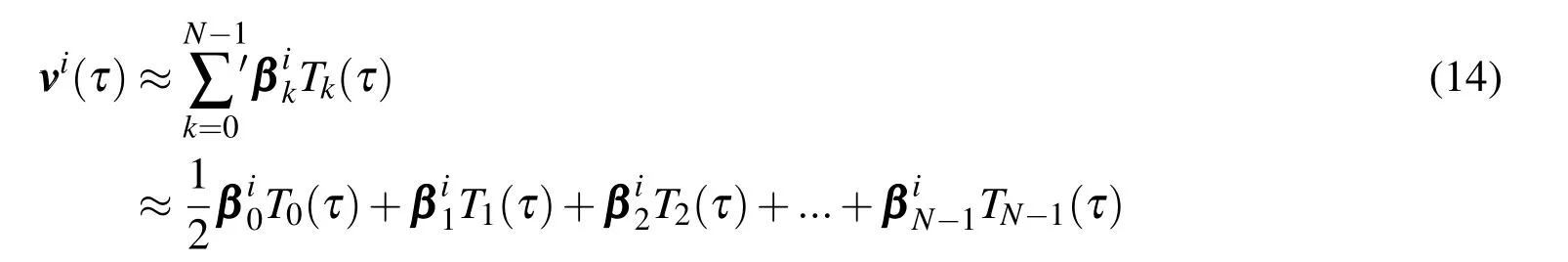
The summation in Eq.14 is from k=0 to N−1 since the analytic integration property causes the Chebyshev order of approximation to increase by one,thus the reason for using the least square formulation for the velocity states instead of the interpolation formulation.

A separate Chebyshev polynomial sequence of order(N−2),with M=N CGL samples,is used to approximate the integrand on the right hand side of Eq.11

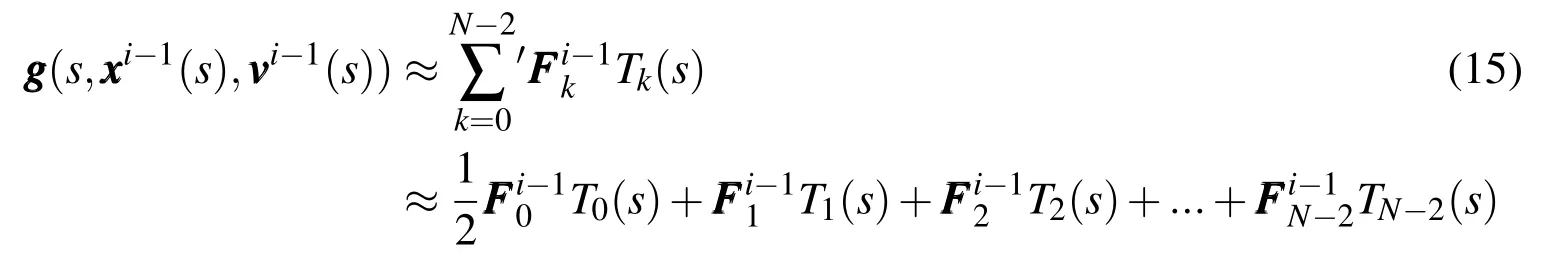
again using the least squares approximation formulation.

Combining Eqs.13 through 15,updates to the integrand and state coefficients take the form

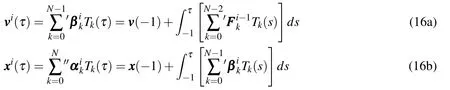
where vvv (−1)and xxx(−1)are the initial conditions of the velocity and position states.Eq.16a is a Picard iteration,and Eq.16b is a kinematic update.Notice that integrating the acceleration approximation of Eq.15 naturally increases the order of the Chebyshev series by one to obtain the corresponding velocity approximation,and by two to obtain the corresponding position approximation.The(usually small)highest order terms in Eqs.16a and 16b could be truncated to enforce an ad hoc desire to approximate position,velocity,and acceleration by a degree N−2 polynomial,but we avoid these truncations here.All approximation errors arise at the acceleration level,and the velocity and position approximations are constrained to be kinematically consistent.

In Eq.13 the system states are approximated using an Nthorder Chebyshev approximation,sampled at M=N CGL nodes,therefore using the interpolation method.In Eq.15 the integrand function is approximated using an(N−2)th-order Chebyshev sequence,but M=N CGL sample points are still used,therefore using the least squares method.More detail on the distinction between the Chebyshev interpolation and least squares methods,and their implications to MCPI,may be found in Ch.1 of[Macomber(2015)].

The integrand Chebyshev approximation to find the coefficient vectorsis performed directly by evaluating the integrand function on the left-hand-side of Eq.15 at the M+1 CGL sample points.The coefficients are solved by the same method as in the first order MCPI case,by the expression

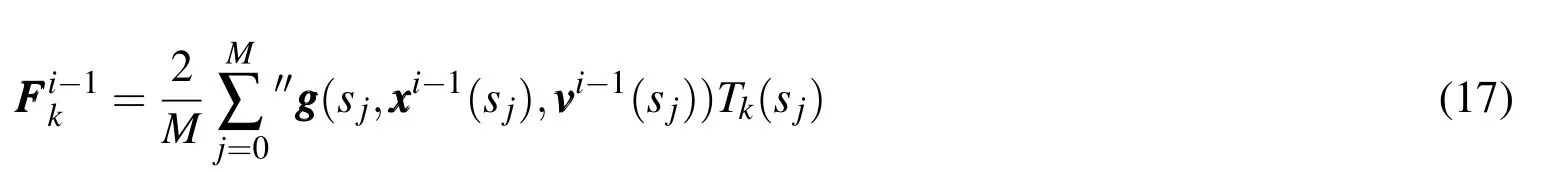
Having calculated the integrand coefficients,the velocity and position state coefficients may be found by solving across the equal sign in Eqs.16.The velocity state coefficientsare related to the integrand coefficientsby the expressions:

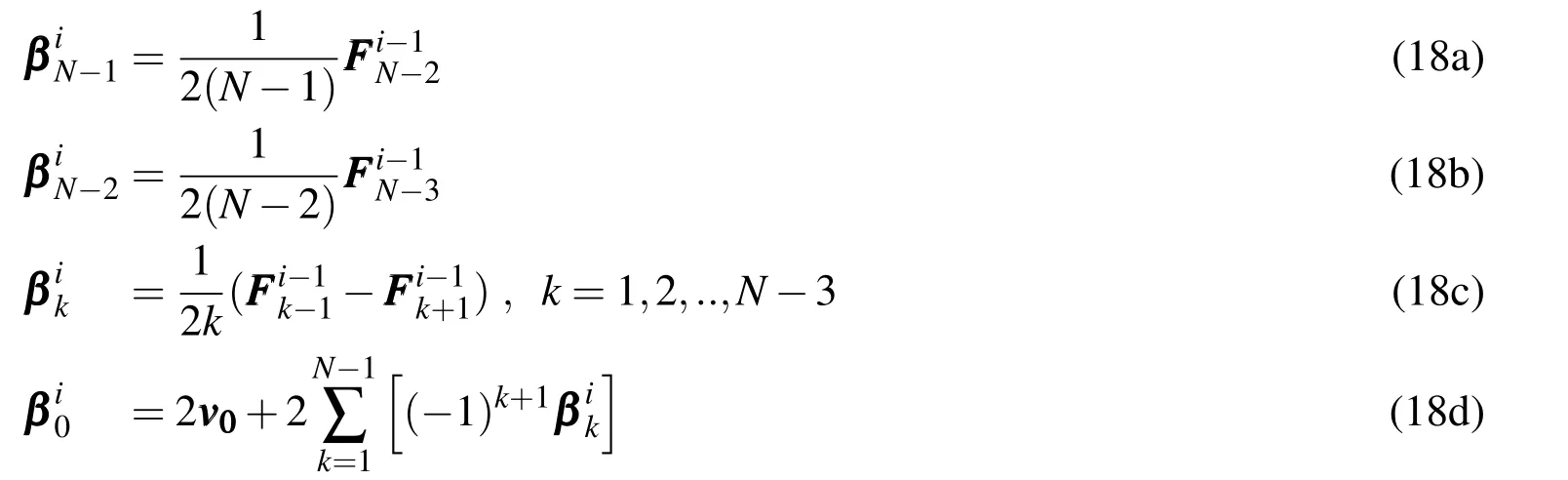
The position state coefficientsare related to the velocity state coefficientsby the expressions:

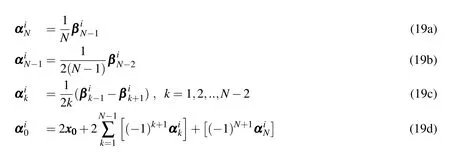
Note the presence of the factor of 2 in the denominator of Eq.18a,which is not present in Eq.19a or in the first-order MCPI derivation.The presence of the factor of 2 is caused by the fact that the least squares Chebyshev approximation formulation is used for both the velocity state coefficients βkand the integrand coefficients FFFk,as opposed to Eq.19a where the position states αkutilize the interpolation version of the Chebyshev formulation.Similarly,in the first-order MCPI the Chebyshev sequence on the left-hand-side of the equation uses the interpolation formulation,and the sequence on the right-hand-side uses the least squares formulation.A related phenomenon may be observed in the difference of structure of the zeroth coefficients(the factor of 2 being absent from the last term)in Eqs.18d,and 19d.Essentially,when the Chebyshev sequence on both sides of the equation uses the least squares formulation,the coefficient expressions will take the form of Eqs.18a and 18d,but when one side of the equation uses the least squares formulation and the other side uses the interpolation formulation,the coefficient expressions will be of the form of Eqs.19a and 19d.

As with the first order MCPI formulation,the second order MCPI may be restructured into a vector/matrix framework. A brief overview is given here, and the details are explicitly presented in[Macomber(2015)].

The ithestimate of the position and velocity states are written as a matrix by stacking the state values for all M+1 CGL sampled times τ0to τMas

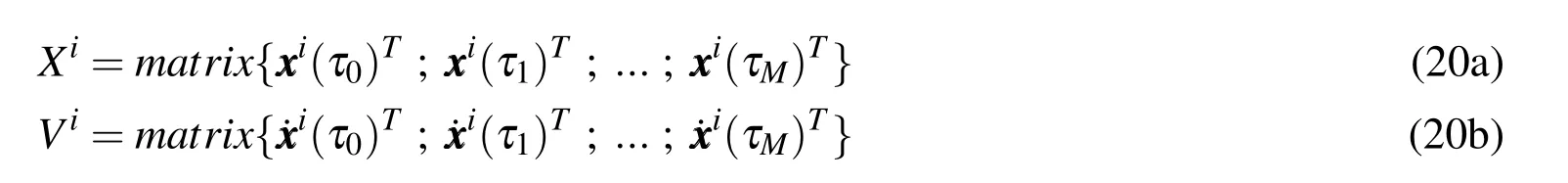
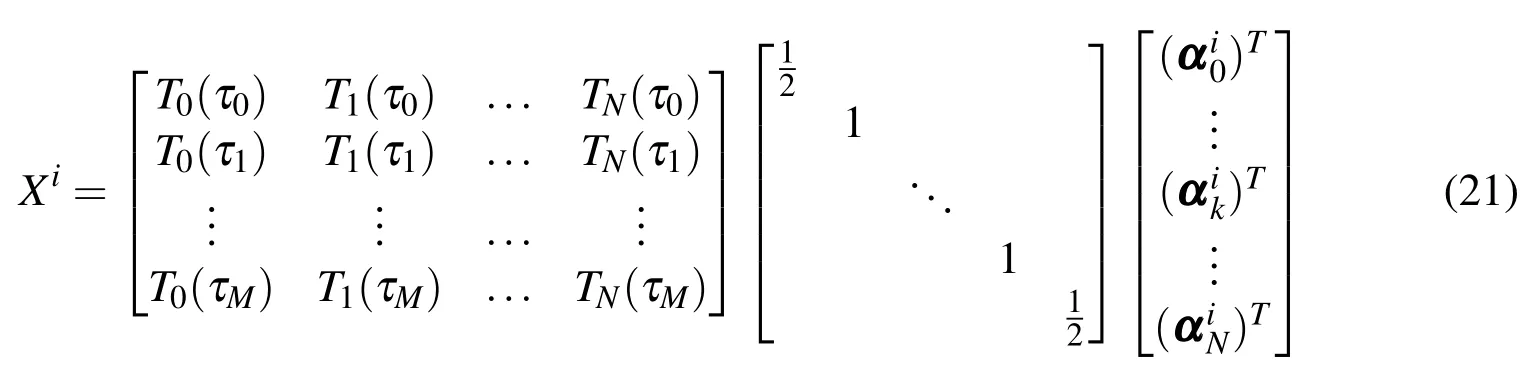
Similarly,Eq.14 for the Chebyshev least squares approximation of the velocity states may be expressed as a vector/matrix equation by

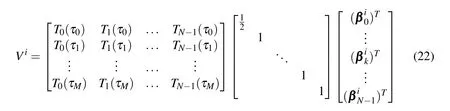
The above two equations may be summarized as

In general,αWis an(N+1)×(N+1)diagonal weight matrix,andαT,a matrix of Chebyshev polynomials evaluated at CGL sampled times τj,is of size(M+1)×(N+1).βWis an N×N diagonal weight matrix,andβTis of size(M+1)×N.Note thathas aas the last term,whereas inβTthe last term is a 1.This is due to the slight differences between the Chebyshev interpolation formulation used to approximate the position states,and the Chebyshev least squares formulation used to approximate the velocity states.

The integrand of the ODE is fit using the least squares Chebyshev approximation.A Chebyshev approximation of order N−2,with M=N CGL sample points is used.During the ithPicard iteration,the(N−1)×n matrix of integrand coefficients Fi−1contains the individual n×1 integrand coefficient vectorsthrough

The integrand coefficient fit,as given by Eq.17,may be written as a vector/matrix expression:

for short.In the above equation,FTTis an(N−1)×(M+1)matrix of Chebyshev polynomials T0through TN−2evaluated at the M+1 CGL sample points,and V is an(M+1)×(M+1)Cheybshev weight matrix.G(Xi−1,Vi−1)is the result of evaluation of the integrand functions at the(i−1)thapproximation of the system states.The similarity in notation between the weight matrix V and the ithvelocity state approximation Viis being used in order to remain consistent with previous MCPI publications.

The Picard iteration to relate the unknown velocity state coefficients βito the known integrand coefficients Fi−1(as given by Eqs.18),and the kinematic constraint relating the unknown position state coefficients αito the(now)known velocity state coefficients βi(from Eqs.19)may be written in matrix/vector form as

βSandαSare of size N×(N−1)and(N+1)×N,respectively,and take the general form

where the top row has the kthterm given by

V0and X0are of size N×n and(N+1)×n,respectively,and are responsible for enforcing the initial boundary conditions for the velocity and position coefficients.βR andαRare square matrices of size N×N and(N+1)×(N+1),respectively,and are defined by

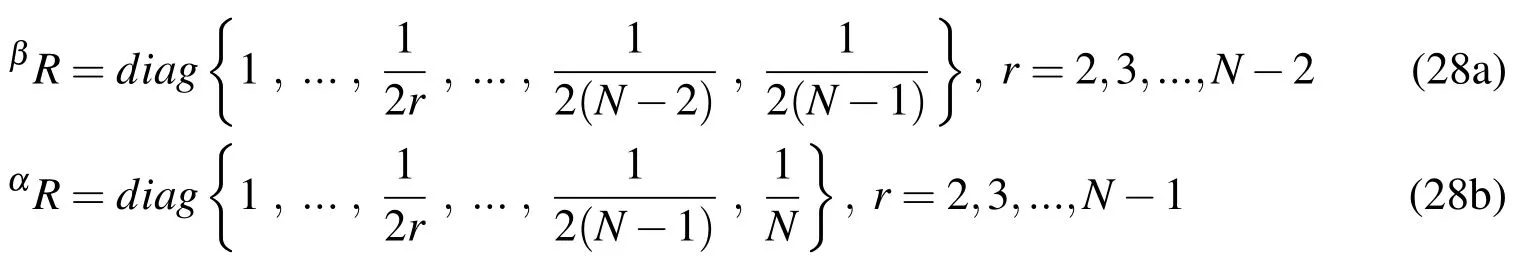
These two weight matrices reflect the difference between using the least squares Chebyshev formulation for both sets of states(as with βiand Fi−1),and using the least squares Chebyshev formulation for one set and the interpolation formulation for the other other(as in the the case of αiand βi),as discussed above.

Summarizing the expressions so far,we have

De fining constant matrices

a Picard update is of the form

Note that the matricesCx,Cγ,andCα,as well as their matrix products,are constant once the order of approximation N,and therefore the number of CGL sample points M,are set.These matrices may therefore be generated once prior to propagating with MCPI,and do not cause any computational overhead during the process of Picard iteration.

2 MCPI Algorithmic Improvements

This section describes several algorithmic improvements to the basic MCPI algorithm that increase the performance when integrating the equations of perturbed orbital motion.Virtually all of these enhancements center on methods to“legally cheat”by drastically reducing the cost of local force function computations without introducing significant approximation errors.These techniques are applicable to broad classes of numerical integration algorithms,although some application specific tuning and validation may be required.

2.1 Radially Adaptive Gravity

Because the Earth is not a perfect sphere with a spherically symmetric mass distribution,the gravitational potential in the vicinity of the Earth is a complicated nonlinear scalar field.In order to compute high precision orbit predictions with a numerical propagator,the local gravitational acceleration must be computed to high precision along the entire orbit trajectory.This local high precision gravity calculation is consistently one of the most computationally expensive aspects of perturbed orbit propagation at state of the art precision.

The gravitation potential field of the Earth at a particular radius,latitude,and longitude(r,φ,λ)is modeled as a spherical harmonic series

where Cl,m,Sl,mare empirically determined coefficients,R is the radius of the Earth,and Pl,mare recursively defined associated Legendre functions[Vallado(2013)].The Cl,mand Sl,mare in fact higher order mass moments that could be computed exactly if the true density distribution and geometry of the Earth were known.These have been“learned”by solving the inverse problem given almost six decades of tracking actual satellite orbits.Implemented as a computational subroutine,E-q.32 and its gradient are a double for loop over the degree l and order m of the gravity field.The max degree and order are generally chosen by the user/analyst depending upon the orbital regime,the required accuracy of the solution,the available computational resources,or other heuristic criteria.The equation above is for a “square”gravity model,meaning lmax=mmax.

We mention that lmaxexceeding 200 is required if we wish to compute“atmosphere skimming”low altitude orbits with state of the art precision.Therefore the gravitational potential series in Eq.32 and the three vector components of its gradient can result in tens of thousands of terms to be computed.For this reason,previous researchers have developed methods to decrease the computational burden of gravitational field calculations.These methods generally surrender the elegance of the global spherical harmonic series in favor of local approximation of the higher degree and order terms.Junkins developed an a priori finite element method gravity representation,designed for in- flight applications,which allowed the local gravitational perturbation potential to be modeled before flight using a lower order 3D orthogonal basis set,greatly reducing the in- flight computational cost[Junkins(1976);Singla and Junkins(2009);Engels and Junkins(1980)].Bani-Younes and Junkins revisited this work using orthogonal Chebyshev polynomials and modernized it for recent processor developments and parallel computing architectures[Bani-Younes(2013);Junkins,Bani-Younes,Woollands,and Bai(2012)].These methods,while greatly reducing the necessary real-time computations required in order to calculate a high fidelity gravity acceleration,do so at the cost of added memory requirements(to store the local FEM coefficients).Looking at the problem from a different direction,Vallado quanti fied the output trajectory error as a result of truncating the gravity series at varying degree and order,and drew conclusions about the degree and order required to achieve certain trajectory propagation errors[Vallado(2005)].Other papers on this topic include[Arora and Russell(2015);Born,Born,and Beylkin(2010);Arora,Vittaldev,and Russell(2015)].In this section we present another method,conceptually related to Vallado’s approach,to decrease the real-time computational cost of high-precision gravity approximation.

The gravitational acceleration is computed with a gradient of the potential field

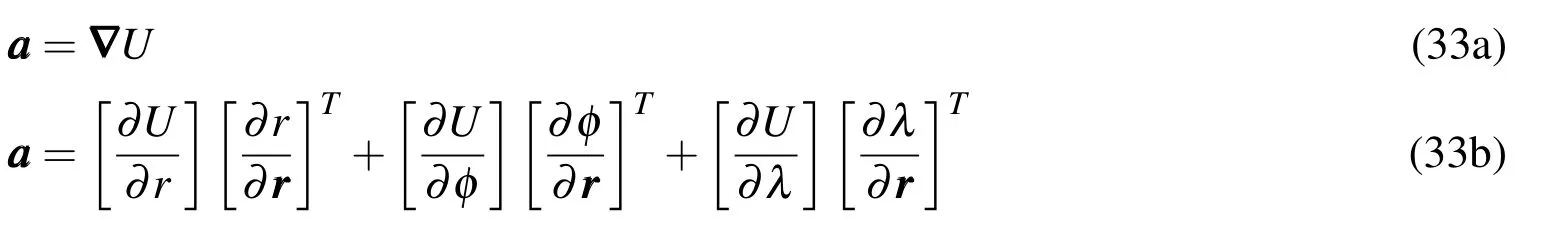
where each of the partial derivative terms of the potentialis also a double summation with the same ingredients as the potential series of Eq.32.For instance,the partial derivative of the potential with respect to the radius is

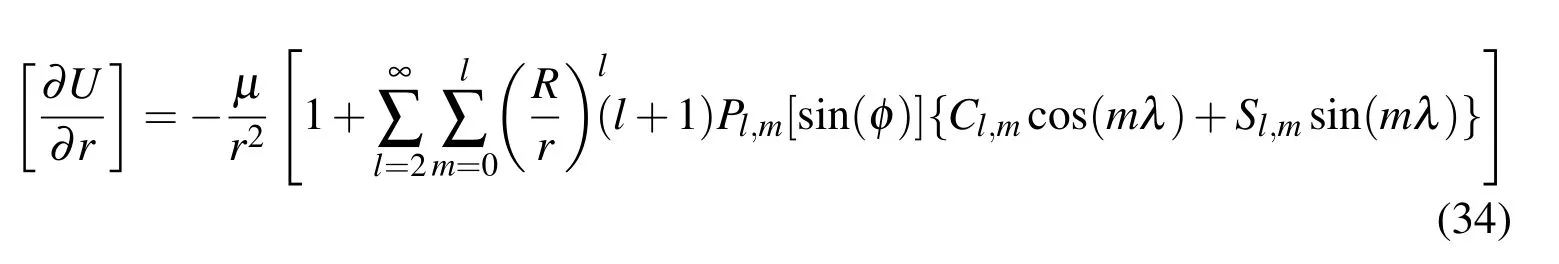
The acceleration exhibits similar radial trends with respect to the number of relevant terms as the potential field.This is illustrated in Fig.1,which shows contours of the local variations of the radial acceleration.This is calculated using the EGM2008 spherical harmonic gravity model with maximum degree and order 200[Pavlis,Holmes,Kenyon,and Factor(2008)].Near the surface of the Earth the acceleration perturbations are largest,and spatially vary quite rapidly,because of the large number of non-negligible terms in the series of Eq.32.However,at a radial distance of 3 Earth radii the acceleration spatially varies much more smoothly and is two orders of magnitude smaller.

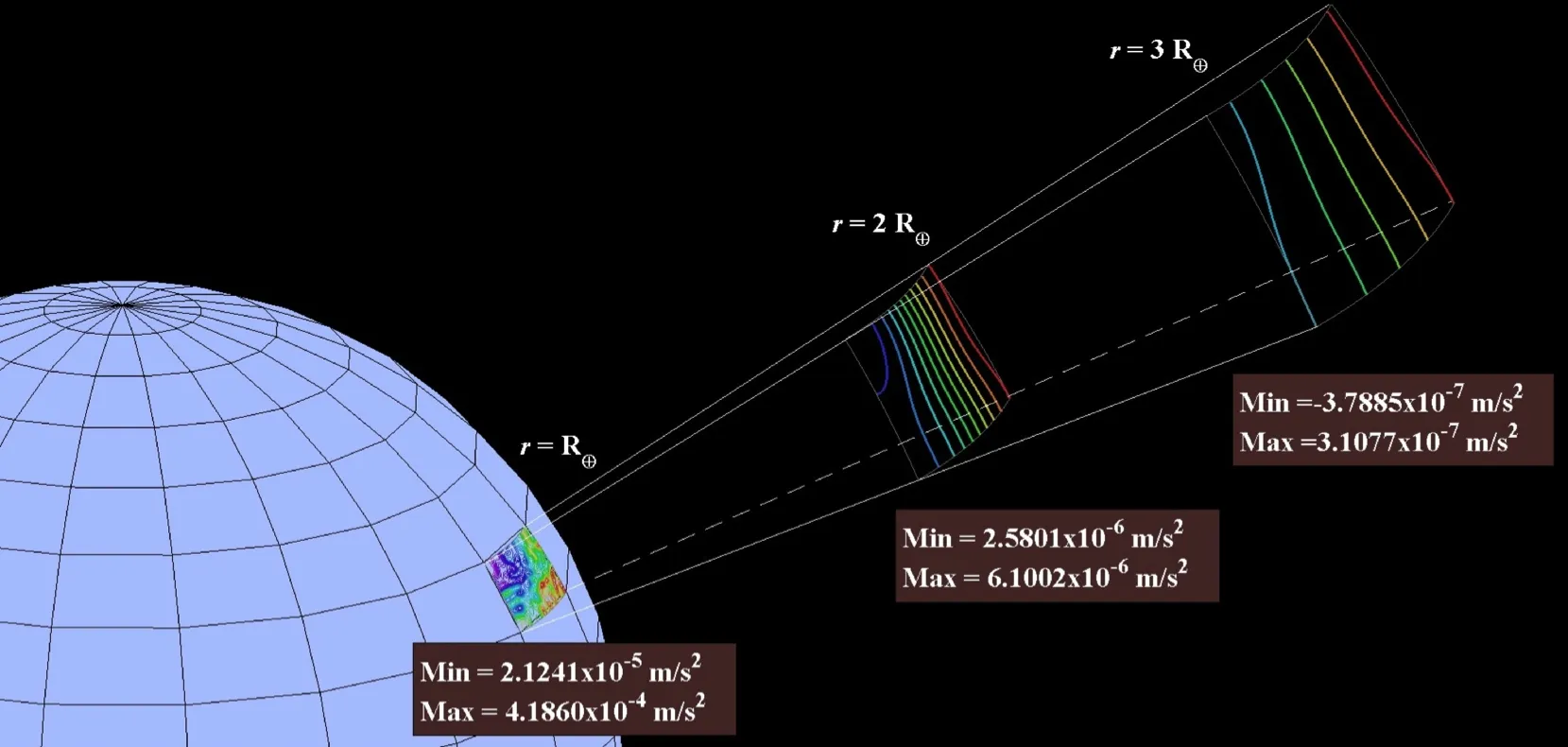
Figure 1:Local variations of the gravitational acceleration at various radii.

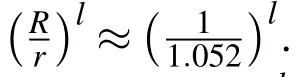
Because the equation of gravitational acceleration contains a double summation,the computational cost of evaluating a series of maximum degree and order L varies quadratically with L.The relative computational cost of a gravity model of order L compared to a model of some higher order Lmaxis proportional to

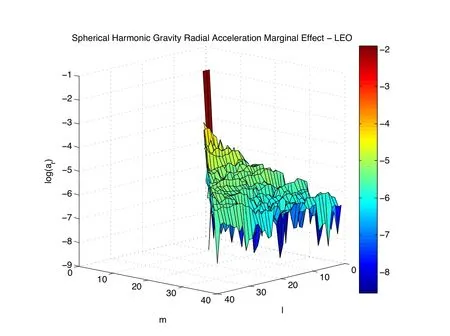
Figure 2:Marginal radial gravitational acceleration magnitude as a function of spherical harmonic degree and order,in LEO regime.

Figure 3:Marginal radial gravitational acceleration magnitude as a function of spherical harmonic degree and order,in GEO regime.

At an arbitrary point along an eccentric orbit,if a desired acceleration precision may be achieved with a gravity model of order L as would be achieved using the model of arbitrarily determined order Lmax,then the equivalent gravity cost E of model order L scales as Eq.35.

This motivates the discussion of a radially adaptive spherical harmonic gravity model for orbit propagation using MCPI, first presented in[Probe,Macomber,Woollands,and Junkins(2015)].A desired acceleration precision δ is specified by the user/analyst.At each gravity series function evaluation point(with instantaneous orbital radius r)around the orbit,an Lthdegree/order gravity series is evaluated,where L=L(r,δ).The L at each evaluation point is chosen such thatwhere lmaxand mmaxare the degree and order of the highest order term in the double summation with magnitude greater than δ,and Lmaxis the heuristically chosen maximum degree and order that would otherwise be used for every function evaluation.This implies no assumption of a monotonically decreasing series.Neither does it cherry-pick higher order harmonic terms while neglecting intermediate order terms,a situation which could potentially systematically eliminate harmonic gravitational perturbations.

An empirical method for a one-time a priori determination of the appropriate radially adaptive maximum gravity degree/order L=L(r,d) is straightforward to implement.Looping over the individual terms in the double summation of the spherical harmonic gravity series allows the marginal contribution from each term to be studied.lmaxand mmax,the maximum degree and order of terms which contribute more than tolerance δ,are located in the process.Choosing to maintain a square gravity field for simplicity,we find the maximum required degree and order at a given spatial position(r,φ,λ)as L=max{lmax,mmax}≤ Lmax.To ensure that the spatial sampling is representative and comprehensive,1000 sample points are distributed uniformly around the unit sphere [Leopardi (2006)]. The process of determining the required degree and order is performed at all uniformly spaced sample points on a spherical shell of radius r.Choosing the most conservative value gives L=L(r,δ).The process is repeated for a range of r values(rmin≤r≤rmax)from Low Earth Orbit to above Geostationary Earth Orbit.

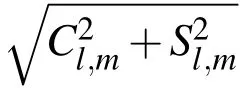
Regardless if the empirical method or the more elegant semi-analytic method is used,a cosine-like sampling ξ is defined to determine the radii at which to evaluate the gravity model(as opposed to linearly spaced sampling):

where−1≤ξ≤1.This sampling scheme allows for a concentration of evaluation points near the Earth’s surface where the rate of change in the size of the perturbations is the greatest.Additionally,it allows the required degree and order L=L(r,δ)to be approximated with orthogonal Chebyshev polynomials,using a procedure developed by Junkins and Bani-Younes[Junkins,Bani-Younes,Woollands,and Bai(2012);Bani-Younes(2013)].

The result of both the empirical and the semi-analytic method is a two-dimensional look-up table of the required maximum gravity degree and order L,as a function of radius r and desired acceleration tolerance δ.The resulting look-up table(generated by the empirical method)is plotted as a surface in Fig.4,which was generated for the EGM2008 spherical harmonic gravity model[Pavlis,Holmes,Kenyon,and Factor(2008)].The values are truncated at maximum degree and order 100 in this example,but the procedure is valid for arbitrary maximum degree and order,and a similar surface may be generated for any value of L.

To demonstrate the effect of radially adaptive gravity,a single orbital period of a GEO Transfer Orbit is propagated,starting from perigee,using MCPI.A GEO

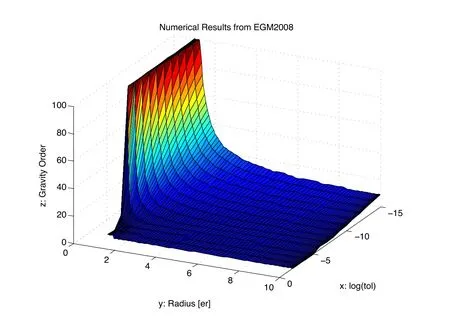
Figure 4:Required spherical harmonic gravity degree and order as a function of radius and desired acceleration tolerance.

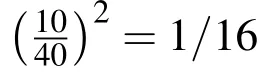
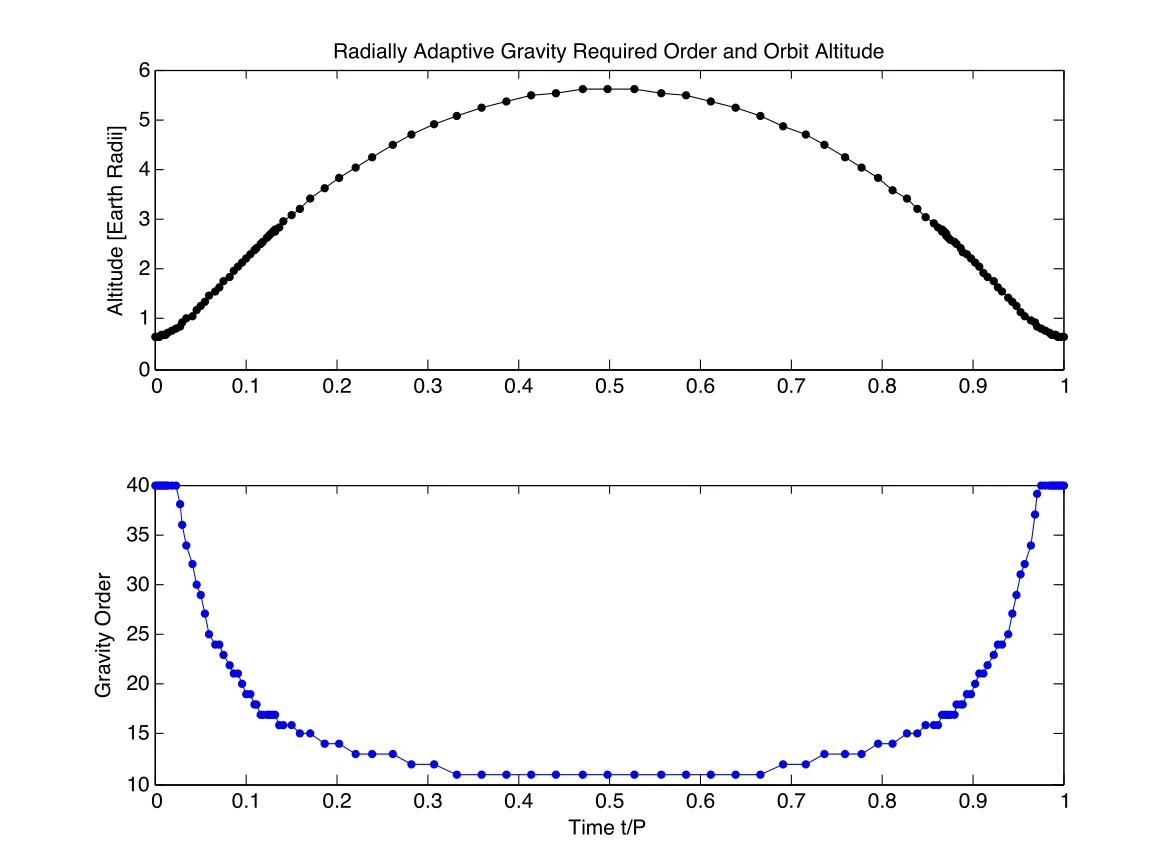
Figure 5:Radially adaptive gravity method-instantaneous orbital altitude and required maximum degree and order L along GEO Transfer Orbit.

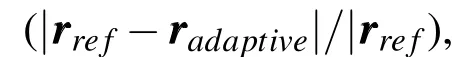
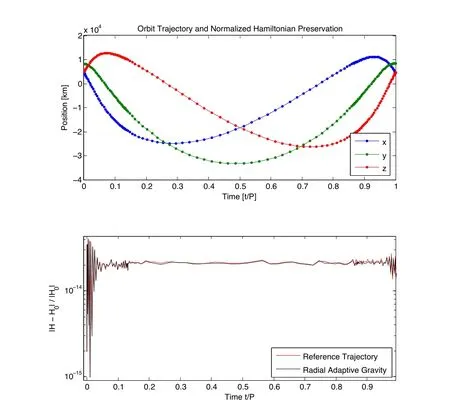
Figure 6:Radially adaptive gravity method-orbit position states and normalized Hamiltonian preservation along GEO Transfer Orbit.

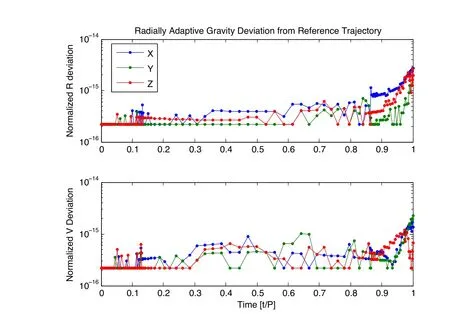
Figure 7:Radially adaptive gravity method-deviation from reference trajectory along GEO Transfer Orbit.

2.2 Taylor Series Gravity Model

The radially adaptive method described in the previous section is a simple,elegant means for reducing the cost of computing accelerations from the global gravity model.A multiple fidelity approach to evaluating force functions can greatly reduce computational effort in an iterative numerical algorithm such as MCPI or Implicit Runge-Kutta(IRK)[Bradley,Jones,Beylkin,Sandberg,and Axelrad(2014);Jones(2012);Aristoff and Poore(2012);Probe,Macomber,Kim,Woollands,and Junkins(2014)].The motivation for this is the fact that,during the initial few iterations(when the nodal convergence errors have 10−4or greater relative error),it is computationally wasteful to calculate a full accuracy spherical harmonic gravity series at each evaluation point.Towards the end of the iteration process,when MCPI has converged in position/velocity accuracy to seven or more digits,the trajectory itself is not spatially changing very much from iteration to iteration,but higher accuracy in acceleration is required to converge further.The essence of the multiple fidelity force model strategy is to calculate local perturbation forces(in the vicinity of each node)only as accurately as is required to keep MCPI smoothly converging,or about one to two digits more precisely than the local solution accuracy.This approach is generally valid for all smooth and continuous environmental perturbation force models,but we focus here on gravitational forces because in many cases they are often the most computationally expensive.

The multiple fidelity gravity method is shown in Fig.8.Three gravity models of varying complexity are utilized throughout the process of Picard iteration,the simplest being the first five zonal harmonics J2through J6,which are computationally trivial to calculate in comparison to full order spherical harmonic gravity.During the Picard iteration in which a higher fidelity force model is used for the first time,a local Taylor series correction at each node is calculated that locally approximates the higher fidelity model to sufficient precision without requiring further“full”force evaluations.Subsequent Picard iterations do not require the calculation of the higher fidelity gravity model,merely an evaluation of the J2through J6model to which the Taylor correction is added,therefore accounting locally for the difference between the approximate and the high-order gravity model.An a priori study can rigorously establish the validity of these approximations as a function of the local displacement from the nodal coordinates where the Taylor series approximation is calculated.

The full-order gravitational accelerationat a point rrr=[x,y,z]Tis a spherical harmonic series with some conservatively specified maximum degree and order.Typically the maximum degree/order value is chosen based upon prior insights into the desired fidelity of the output solution,the computational resources available,and the orbital regime of interest.The methods underlying the radially adaptive gravity method can be invoked to make these traditionally heuristic decisions more rigorous.For the present discussion,we adopt a low order approximate gravity model:the gravitational acceleration due to two-body Keplerian motion plus the contributions of the first five zonal harmonic gravity terms J2through J6,which we designateThe difference between whatever full-order gravitational acceleration model is selected and the zonal approximate gravitational acceleration is Taylor expanded at an arbitrary pointnear the initial pointas

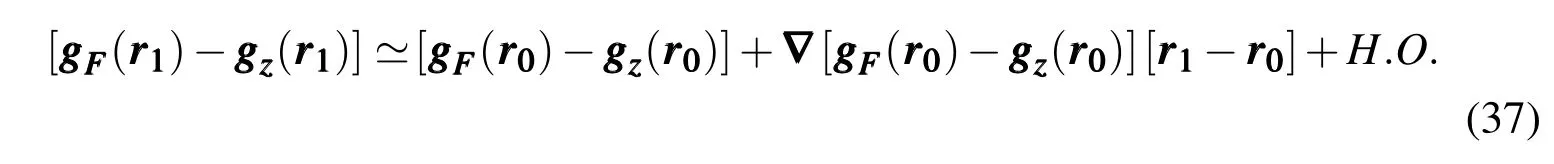
Re-arranging the above equation and neglecting the higher-order terms provides an approximation of the full-order gravityas

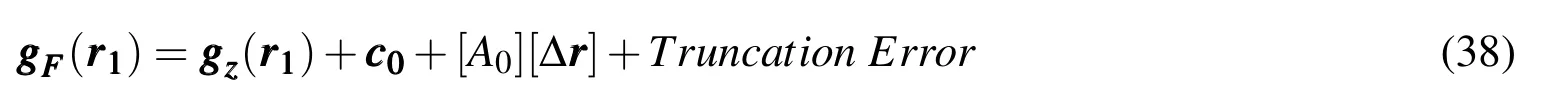
Remarkably,MCPI is able to achieve a large computational speedup by using a zeroth order Taylor series approximation in the multiple fidelity gravity method,while still being able to achieve arbitrarily high accuracy.This is becauseis small,and over small regions the discrepancy betweenandis approximately constant at each node.Fig.9 shows a comparison of computation time and function evaluation count for MCPI and other state of practice numerical propagators,applied to an eccentric orbit with a perigee radius in LEO[Probe,Macomber,Kim,Woollands,and Junkins(2014)].In these plots,MCPI without the multiple fidelity gravity method is labeled “MCPI”,and MCPI with the zeroth order Taylor series multiple fidelity method is labeled “TCA-MCPI”.The zeroth order Taylor approach is also generally useful during the analogous convergence process of Implicit Runge Kutta propagators[Bradley,Jones,Beylkin,Sandberg,and Axelrad(2014);Jones(2012);Aristoff and Poore(2012)].

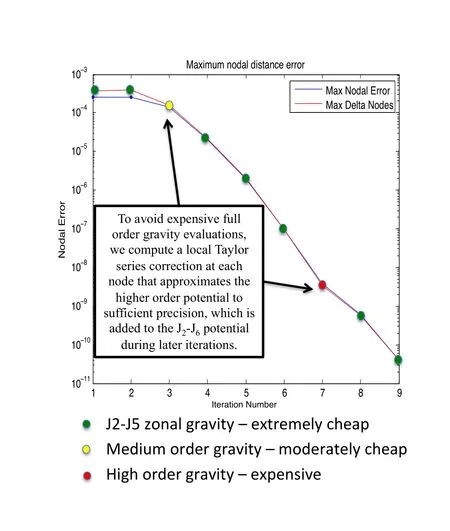
Figure 8:Representative MCPI convergence error history using the multiple-fidelity gravity method.

Figure9:MCPI zeroth order Taylor series propagation,computational performance compared to state of practice numerical propagators for eccentric LEO orbit.

Within a single instance of MCPI,utilizing a first order Taylor approximation does not provide much improvement over the zeroth order approximation because the nodal corrections between iterations are generally small,especially at the end of the convergence process when the highest approximation accuracy is required.However,an important benefit of the first order Taylor method is that it can increase the domain of validity of the Taylor approximation beyond that of the zeroth order method.This means that after having calculated the local Taylor approximation to the gravity field once,neighboring trajectories within the domain of validity may be propagated essentially “for free”.This is ideal for propagating particle trajectories in the vicinity of a reference trajectory,for instance within Monte Carlo analysis or uncertainty propagation,or within a particle or Sigma-Point filter.There is,however,a moderate computational penalty when propagating the reference trajectory,as the gradient A0matrix must be calculated.

A0can be computed analytically during the propagation of the reference trajectory(within the MCPI convergence loop)by taking partial derivatives of the spherical harmonic series,which adds an additional computational penalty beyond the cost of the series itself(estimated 15-20%extra computation time).These analytic partial derivatives are the same computations that are required to numerically propagate the perturbed state transition matrix[Read,Junkins,and Bani-Younes(2015)].In this case,the position difference vectorcomes from the nodal corrections between Picard iterations.

Alternatively,the gradient matrix A0may be computed numerically by performing manual perturbations away from a reference trajectory and solving the system of equations[Macomber,Probe,Woollands,and Junkins(2015a)].

To numerically solve for the gradient matrix, MCPI is first used to propagate a high-fidelity reference trajectoryA Taylor expansion about time-sampled positionsalong the reference trajectory is given by Eq.38,which can be rearranged to give

Evaluating the full-order gravity functionand the zonal gravity functionat the pointmeans the left hand side of Eq.39 is a known quantity,which is renamed.This gives

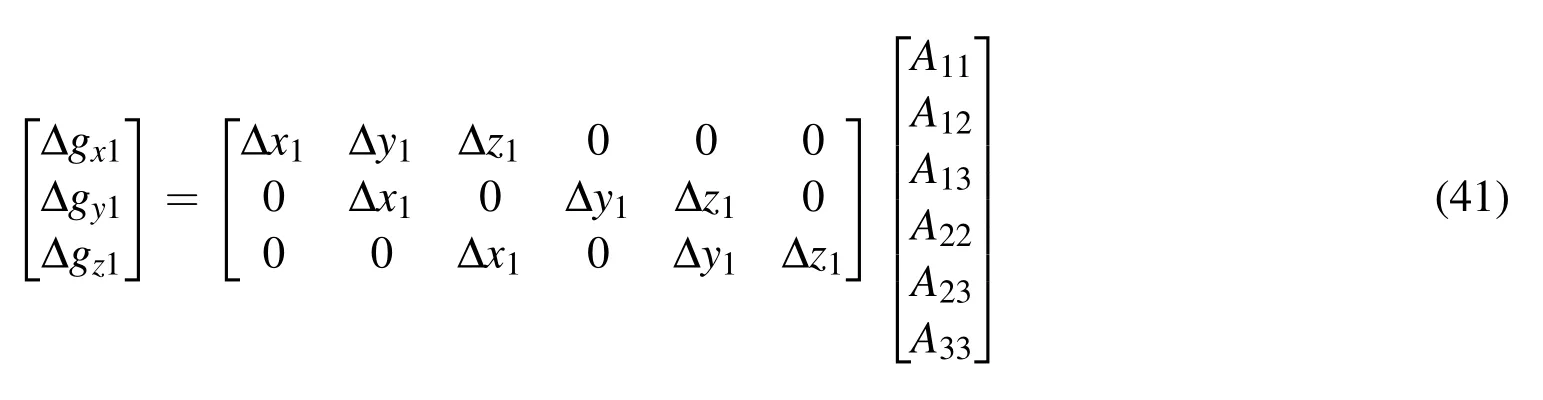
Eq.41 is a matrix system of the form,where the terms,andforming the B matrix are the elements of thevector.Three independent offsets from the reference trajectory to positionsandare performed.Stacking the transmuted system of Eq.41 from the three offsets giveswhich is a(9×1)vector,B which is a(9×6)matrix,and a which is a(6×1)vector containing the unknown elements of the A0matrix.This system can be solved using the normal equations of least squares

to find the best estimate of the unknown elements aiof the A0matrix.It would seem that two offsets away from the reference trajectory would provide a(6×6)B matrix that could be inverted directly to solve for the aa a vector,but in practice this(6×6)B matrix is singular and non-invertible.This is easily cured by introducing one or two additional evaluations and using a least square inverse.

This first order Taylor series gravity approximation is ideal for propagating trajectories in the vicinity of the reference trajectory,such as in a Monte Carlo analysis or during the process of uncertainty propagation.The gradient matrix along the reference trajectory can be calculated ahead of time,thereby allowing neighboring trajectories to be propagated without performing any high- fidelity gravity evaluations during the MCPI iteration process.This means that using MCPI to propagate trajectories near the reference trajectory can be done to within the accuracy limit of the local first order Taylor approximations significantly more quickly.Figs.10 and 11 show a trajectory propagated using the first order Taylor approximation near a GEO reference trajectory of the Telemetry Data Relay Satellite(TDRS-11)over a period of 20 days(20 orbits).Fig.10 is the spatial deviation of the orbit away from the reference orbit,which varies between roughly two to ten kilometers,starting from an initial deviation of roughly 3.5 kilometers.This orbit was propagated using TCA-MCPI but the high- fidelity gravity evaluations were replace by the Taylor series approximation with respect to the reference trajectory.Fig.11 shows the Hamiltonian preservation of the numerically propagated reference trajectory,and of the neighboring trajectory propagated using the first order Taylor series gravity approximation.The Taylor series solution is able to conserve the Hamiltonian to a precision of about 10−12for this near-GEO case.

Using the same initial deviation of roughly four kilometers for a LEO orbit similar to that of the International Space Station,the first order Taylor series gravity is able to preserve the Hamiltonian to a precision of about 10−9over 20 orbits(1.25 days).Note that for the Low-Earth Orbit ISS-like case,an initial deviation of 3.5 kilometers is a much larger relative deviation when normalized by the orbital radius than it is for the GEO orbit which has a semi-major axis of about 42 thousand kilometers.Furthermore the LEO case gravity model is much more nonlinear than the GEO case.

The Hamiltonian preservation is not a perfect measure of the obtainable solution accuracy of a numerical propagator(especially for these near circular reference orbits),but it is a reasonable metric to show that high fidelity solutions can be attained with vastly reduced computational cost.If more precision is required from the final propagated solution after the first order Taylor series gravity has converged to its achievable accuracy limit,further MCPI iterations using the zeroth order Taylor series may be performed to achieve arbitrarily accurate trajectories.

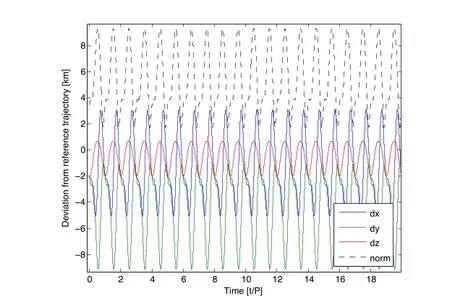
Figure 10:Spatial deviation of first order Taylor series trajectory in neighborhood of TDRS-11 reference orbit.

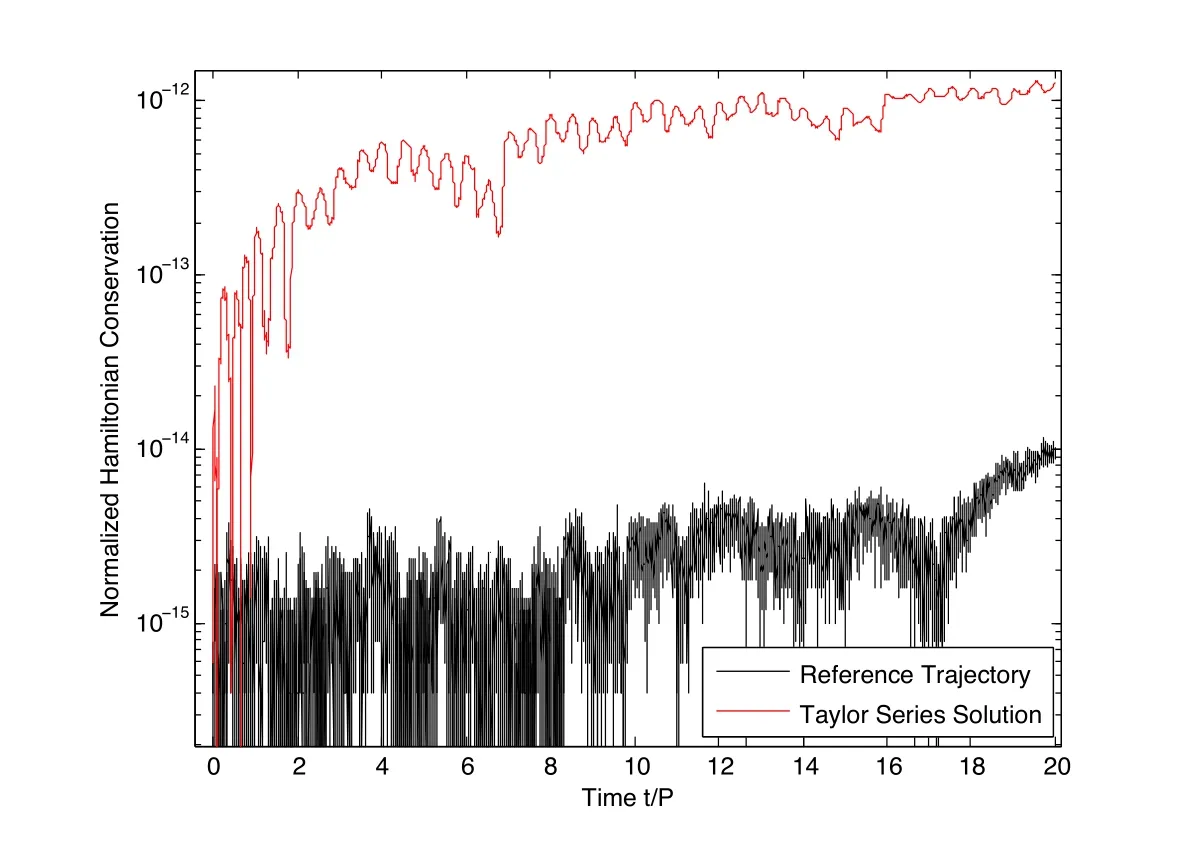
Figure 11:Hamiltonian preservation of reference orbit and neighboring trajectory with first order Taylor gravity approximation.

2.3 Cold/Warm/Hot Start

MCPI,when applied to the problem of perturbed orbit propagation,has been shown to be able to converge for segment lengths of up to several orbital periods,even with a completely uninformed initial approximation[Bai and Junkins(2011a)].Typically,if no a priori approximation of the system state trajectories is available, the value of the states at all CGL nodes is initially set equal to the boundary conditions.This method is called the “cold-start”method.However,any initial approximation to the true dynamics will allow MCPI to converge to the true solution in fewer iterations.If the initial approximation is sufficiently good(with,say,10−4or smaller relative errors)then we can immediately invoke the force approximation ideas from the previous section,and typically need only one full force evaluation per node to achieve final convergence.

The equation of generally perturbed orbital motion iThe dominant acceleration force acting on an object in Earth orbit at instantaneous positionis the Keplerian gravity termAdded to this are other disturbance forcescaused by the gravitation potential of the non-spherical Earth,atmospheric drag,third body gravitational effects from the Sun and Moon,solar radiation pressure,and other complex forces due to the physics of motion in the space environment.Approximate solutions to the generally perturbed Earth-orbiting satellite problem are available.It is logical to invoke these and other insights to establish a bet-ter starting orbit approximation than the cold-start method.Implicit Runge Kutta(IRK)algorithms have previously utilized analytic and semi-analytic methods to provide an initial estimate for perturbed orbit propagation[Jones(2012);Aristoff,Horwood,and Poore(2012)].

A two-stage initial orbit approximation method can greatly reduce the amount of required MCPI computation for propagation of more than one orbit period.The first step is to “warm-start”MCPI at the CGL nodes during the first lap around the orbit using the analytic Keplerian solution,or a semi-analytic solution for perturbed motion.This won’t be perfect because the perturbation forces will cause the true motion to deviate from the approximate solution,however typically a starting estimate accurate to three or more significant digits will result.Allowing MCPI to converge and then saving the difference between the warm start estimate and the final converged solution gives an Encke-type description of the deviation(at the nodes)of the true motion from the starting approximation.The next lap around the orbit,MCPI can be warm started with the same approximate solution(re-osculated with perigee position and velocity at the start of the second orbit),and then the deviation from the previous warm start can be applied on top of that to give the“hot-start”.

The motivation for this idea is that the non-two-body perturbations are highly correlated on successive orbits.Asking the question“How did the previous warm start differ from the final convergence?”is useful to trend-sense a correction for the next pass through a neighboring part of the force field.While not rigorous,it is easy to verify that this“previous Encke departure motion”gives a significantly improved starting iterative.In LEO,the short orbital period means that perturbations are very similar on each trip around the orbit relative to the longer timescale of the Earth rotation.Near GEO,the dominant perturbation terms are the first few zonal harmonic gravity terms,which are symmetric with respect to Earth rotation.Typically the hot-start process gives a starting approximation with errors in the 5th significant figure or better.This process is illustrated heuristically in Fig.12.Note that this figure is not drawn to scale;the deviations are many orders of magnitude smaller than the orbit radius in practice.

A reasonable starting approximation to the true dynamics can be obtained by the analytic solution to the problem of Keplerian motion,the Lagrange/Gibbs analytical F and G solution[Schaub and Junkins(2014)].A better approximation to the dynamics of perturbed orbit approximation may be obtained with a semi-analytic solution,which takes into account the time-averaged secular effects of a subset of the disturbing accelerations[Hoots and Roehrich(1980);Hoots,Schumacher Jr.,and Glover(2004);Vallado,Crawford,and Hujsak(2006);Martinusi,Dell’Elce,and Kerschen(2015)].

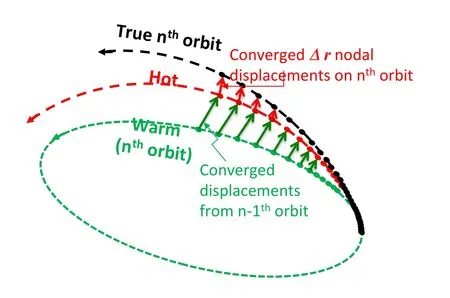
Figure 12:Heuristic schematic of cold/warm/hot-start methods for MCPI perturbed orbit propagation.

The analytic solution of Keplerian motion,or any of the semi-analytic methods,may be used to warm-and hot-start MCPI by providing an initial trajectory estimate.Fig.13 demonstrates the effectiveness of the warm-and hot-start methods using the F&G analytic solution.In this figure,the orbit being propagated is a circular GEO orbit,with spherical harmonic gravity as the only perturbation.With no a priori information(“cold-start”),MCPI is able to converge in 14 iterations,from a large normalized relative nodal error(normalized by the initial conditions)on the order of 1(since the initial boundary condition values is used at all nodes).This is indicated by the black curve in the figure.Warm-starting each node along the trajectory with the analytic F and G solution brings the initial error down three orders of magnitude,to around 10−3.MCPI is able to converge in 11 iterations,as indicated by the blue curve.After propagating all the way around the orbit a single time,the initial trajectory estimates on the subsequent orbit can be hot-started.This provides an initial error on the order of 10−5and allows MCPI to converge in 9 iterations,as indicated by the red curve.Eliminating iterations means eliminating expensive force function evaluations and computational overhead.It also means that the local force approximations(from Sec.2.2)can be invoked to make all subsequent iterations extremely inexpensive.Warm-starting on the first trip around the orbit is able to reduce computational cost by roughly 20%,and hot-starting on subsequent trips around the orbit reduces cost by roughly 35%.Invoking local force approximations greatly reduces the cost further.

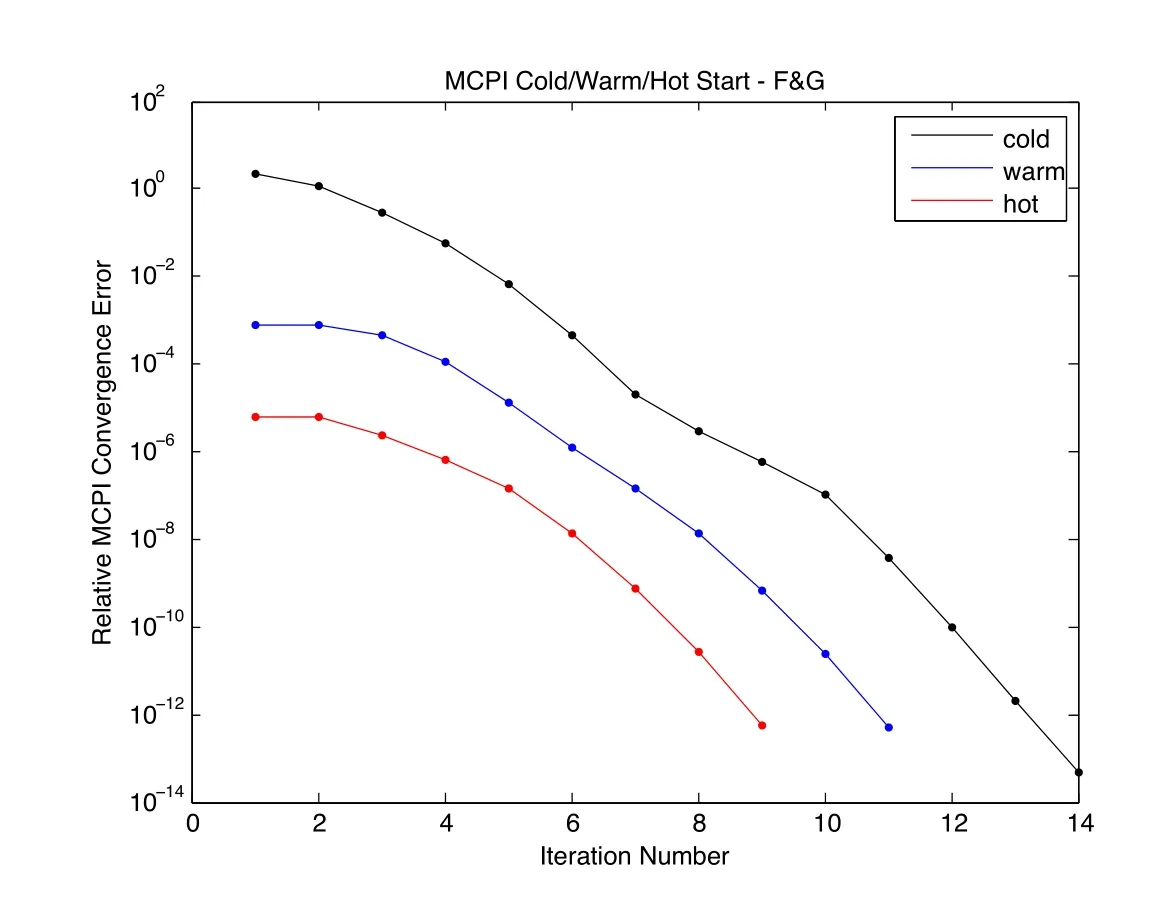
Figure 13:MCPI cold/warm/hot-start convergence trends using F&G analytic solution on GEO orbit.

If the error tolerance for the results shown in Fig.13 is set to 10−8(sub-meter precision)instead of 10−12,hot-started MCPI converges in 5 or 6 iterations.As discussed in Sec.2.2,this can readily be accomplished with only one expensive“full” gravity evaluation per node due to the fixed point nature of MCPI convergence.For the implemented force model,the utilization of local force approximations dramatically accelerates all of the computations after a relative error of 10−5is achieved,and the hot-start process usually allows this approximation on the very first iteration.Thus in Fig.13 we see that the hot start process converges to engineering precision(sub-meter orbit:～ 10−8relative error)in only 6 iterations,and only the first of these requires a full force evaluation at each node.This is the key to computational Efficiency.

The F&G analytic(Keplerian)solution does not take into account any perturbations.The semi-analytic solutions,for instance SGP4[Hoots and Roehrich(1980)],take into account a time-averaged effect of zonal harmonic gravity,simple drag,and third-body sun and moon effects.Depending upon the perturbation models considered in the numerical integration,and the orbital regime of interest,the semianalytic methods can provide better warm/hot start initial approximations than the analytic method.However,the analytic method is much simpler to work with.The semi-analytic methods require careful transformation between osculating states(in which the numerical integrator works)and the time-averaged states(in which the semi-analytic methods work).Additionally,different semi-analytic methods work with different time-averaged elements.For reasons of simplicity,the F&G analytic warm/hot start is preferable for stand-alone numerical integration tools.However,if working with(for instance)a legacy toolset that already includes semi-analytic(general perturbations)code,the existing semi-analytic methods may be used to warm/hot start MCPI with better initial estimates than the F&G two-body warm start would provide.

3 Conclusion

This paper presented a set of improvements to basic Modified Chebyshev Picard Iteration for increasing the computational performance of perturbed orbit propagation.Numerically propagating high- fidelity orbits requires evaluation of computationally expensive perturbation force models,and generally these force function evaluations account for the vast majority of computation time.Typically the spherical harmonic gravity series is the most costly to calculate.Modified Chebyshev Picard Iteration is an iterative numerical method,and the force functions must be evaluated on every iteration.Therefore,the total computational cost may be decreased by either reducing the computational cost per iteration,or by reducing the required number of iterations to achieve convergence.A radially adaptive spherical harmonic gravity model,and a multiple fidelity Taylor series approach for evaluating gravity perturbations between iterations,are two methods presented that reduce cost per iteration.A multi-tiered algorithm to establish an initial estimate of perturbed orbit trajectories,especially when propagating for more than one orbital period,is presented and serves to reduce the required number of iterations.

Acknowledgement:We thank our sponsors:AFOSR(Julie Moses),AFRL(Alok Das,et al.),and Applied Defense Solutions(Matt Wilkins)for their support and collaborations under various contracts and grants.

Aristoff,J.M.;Horwood,J.T.;Poore,A.B.(2012): Implicit Runge Kutta Methods for Uncertainty Propagation.In Advanced Maui Optical and Space Surveillance Technologies Conference,Maui,HI.

Aristoff,J.M.;Poore,A.B.(2012): Implicit Runge Kutta Methods for Orbit Propagation.In AIAA/AAS Astrodynamics Specialist Conference,Minneapolis,MN.

Arora,N.;Russell,R.P.(2015):efficient Interpolation of High-Fidelity Geopotentials.Journal of Guidance,Control,and Dynamics.

Arora,N.;Vittaldev,V.;Russell,R.P.(2015):Parallel Computing of Trajectories Using Graphics Processing Units and Interpolated Gravity Models.Journal of Guidance,Control,and Dynamics,vol.38,pp.1345–1355.

Bai,X.(2012): Modified Chebyshev-Picard Iteration Methods for Solution of Initial Value and Boundary Value Problems.PhD thesis,Texas A&M University,2012.

Bai,X.;Junkins,J.L.(2010): Solving Initial Value Problems by the Picard-Chebyshev Method with Nvidia GPUs.Proceedings of the 20th Space flight Mechanics Meeting,San Diego,CA,vol.AAS 10-197.

Bai,X.;Junkins,J.L.(2011):Modified Chebyshev-Picard Iteration Methods for Orbit Propagation.Journal of the Astronautical Sciences,vol.58,pp.583–613.

Bai,X.;Junkins,J.L.(2011):Modified Chebyshev-Picard Iteration Methods for Solution of Boundary Value Problems.Advances in the Astronautical Sciences,vol.140,pp.381–400.

Bai,X.;Junkins,J.L.(2011):Modified Chebyshev-Picard Iteration Methods for Solution of Initial Value Problems.Advances in the Astronautical Sciences,vol.139,pp.345–362.

Bai,X.;Junkins,J.L.(2012):Modified Chebyshev Picard Iteration Methods for Station-Keeping of Translunar Halo Orbits.Mathematical Problems in Engineering,vol.2012,pp.1–18.

Bani-Younes,A.(2013):Orthogal Polynomial Approximation in Higher Dimensions:Applications in Astrodynamics.PhD thesis,Texas A&M University,2013.

Born,B.A.;Born,G.H.;Beylkin,G.(2010):Comparisons of the Cubed-Sphere Gravity Model with the Spherical Harmonics.Journal of Guidance,Control,an Dynamics,vol.33,pp.415–425.

Bradley,B.K.;Jones,B.A.;Beylkin,G.;Sandberg,K.;Axelrad,P.(2014):Bandlimited Implicit Runge Kutta Integration for Astrodynamics.Celestial Mechanics and Dynamical Astronomy,vol.119,pp.143–168.

Chebyshev,P.L.(1857): Théorie des Mécanismes Connus Sous le Nom de Parallélogrammes.Mémoires des Savants étrangers Prèsentès à l’Acadèmie de SaintPètersbourg,vol.7,pp.539–586.

Clenshaw,C.W.;Norton,H.J.(1963): The Solution of Nonlinear Ordinary Differential Equations in Chebyshev Series.The Computer Journal,vol.6,no.1,pp.88–92.

Engels,R.C.;Junkins,J.L.(1980):Local Representation of the Geopotential by Weighted Orthonomal Polynomials.Journal of Guidance,Control,and Dynamics,vol.3,pp.55–61.

Feagin,T.;Nacozy,P.(1983): Matrix Formulation of the Picard Method for Parallel Computation.Celestial Mechanics and Dynamical Astronomy,vol.29,pp.107–115.

Fox,L.;Parker,I.B.(1968): Chebyshev Polynomials in Numerical Analysis.Oxford University Press,pp.31-33.

Fukushima,T.(1997):Vector Integration of Dynamical Motions by the Picard-Chebyshev Method.The Astronomical Journal,vol.113,pp.2325–2328.

Hoots,F.R.;Roehrich,R.L.(1980): Spacetrack Report No.3:Models for Propagation of NORAD Element Sets.Technical report,U.S.Air Force Aerospace Defense Command,1980.

Hoots,F.R.;Schumacher Jr.,P.W.;Glover,R.A.(2004):History of Analytical Orbit Modeling in the U.S.Space Surveillance System. Journal of Guidance,Control,and Dynamics,vol.27,pp.174–185.

Jones,B.A.(2012): Orbit Propagation Using Gauss-Legendre Collocation.In AIAA/AAS Astrodynamics Specialist Conference,Minneapolis,MN.

Junkins,J.L.(1976): Investigation of Finite-Element Representations of the Geopotential.AIAA Journal,vol.14,pp.803–808.

Junkins,J.L.;Bai,X.(2012):On the Solution of Nonlinear Initial and Boundary Value Problems Using a Modified Picard Iteration Algorithm.Tech Science Press:Adventures on the Interface of Mechanics and Control,pp.219–242.

Junkins,J.L.;Bani-Younes,A.;Woollands,R.;Bai,X.(2012): Orthogonal Polynomial Approximation in Higher Dimensions: Applications in Astrodynamics.In Jer-Nan Juang Astrodynamics Symposium,College Station,TX.

Koblick,D.;Poole,D.M.;Shankar,P.(2012): Parallel High-Precision Orbit Propagation Using the Modified Picard-Chebyshev Method.ASME International Mechanical Engineering Congress and Exposition,pp.587–605.

Leopardi,P.(2006):A Partition of the Unit Sphere Into Regions of Equal Area and Small Diameter.Electronic Transactions on Numerical Analysis,vol.25,pp.309–327.

Macomber,B.(2015): Enhancements to Chebyshev-Picard Iteration Efficiency for Generally Perturbed Orbits and Constrained Dynamical Systems.PhD thesis,Texas A&M University,2015.

Macomber,B.;Probe,A.;Woollands,R.;Junkins,J.L.(2015):Parallel Modified Chebyshev Picard Iteration for Orbit Catalog Propagation and Monte Carlo Analysis.In 38th Annual AAS Guidance&Control Conference,Breckenridge,CO.

Macomber,B.;Probe,A.B.;Woollands,R.M.;Junkins,J.L.(2015):Automated Tuning Parameter Selection for Orbit Propagation with Modified Chebyshev Picard Iteration.In 25th AIAA/AAS Space flight Mechanics Meeting,Williamsburg,VA.

Martinusi,V.;Dell’Elce,L.;Kerschen,G.(2015): Analytic Propagation of Near-Circular Satellite Orbits in the Atmosphere of an Oblate Planet.Celestial Mechanics and Dynamical Astronomy,vol.123,pp.85–103.

Pavlis,N.;Holmes,S.;Kenyon,S.;Factor,J.(2008): An Earth Gravitational Model to Degree 2160:EGM2008.In General Assembly of the European Geosciences Union,Vienna,Austria.

Picard,E.(1893):Surl’Applicationdes Méthodesd’Approximations Successives à l’étude de Certaines équations Différentielles Ordinaires.Journal de Mathématiques Pures et Appliquées,vol.9,pp.217–272.

Probe,A.;Macomber,B.;Kim,D.;Woollands,R.;Junkins,J.L.(2014):Terminal Convergence Approximation Modified Chebyshev Picard Iteration for efficient Numerical Integration of Orbital Trajectories.In Advanced Maui Optical and Space Surveillance Technologies Conference,Maui,HI.

Probe,A.;Macomber,B.;Woollands,R.;Junkins,J.L.(2015): Radially Adaptive Evaluation of the Spherical Harmonic Gravity Series for Numerical Orbit Propagation.In 25th AAS/AIAA Space Flight Mechanics Meeting,Williamsburg,VA.

Read,J.;Junkins,J.L.;Bani-Younes,A.(2015):State Transition Matrix Propagation for Perturbed Orbital Motion Using Modified Chebyshev Picard Iteration.In 38th Annual AAS Guidance&Control Conference,Breckenridge,CO.

Schaub,H.;Junkins,J.L.(2014): Analytical Mechanics of Space Systems.American Institute of Aeronautics and Astronautics,pp.513-519,third edition.

Shaver,J.S.(1980): Formulation and Evaluation of Parallel Algorithms for the Orbit Determination Problem.PhD thesis,Massachusetts Institute of Technology,1980.

Singla,P.;Junkins,J.L.(2009): Multi-Resolution Methods for Modeling and Control of Dynamical Systems.CRC Press.

Vallado,D.A.(2005):An Analysis of State Vector Propagation Using Differing Flight Dynamics Programs.In AAS/AIAA Space Flight Mechanics Conference,Copper Mountain,CO.

Vallado,D.A.(2013): Fundamentals of Astrodynamics and Applications.Microcosm Press,pp.538-547,fourth edition.

Vallado,D.A.;Crawford,P.;Hujsak,R.(2006):Revisiting Spacetrack Report#3.In AIAA/AAS Astrodynamics Specialist Conference,Keystone,CO.

Woollands,R.M.;Read,J.L.;Macomber,B.;Probe,A.B.;Bani-Younes,A.;Junkins,J.L.(2015): Parallel Generation of Extremal Field Maps for Optimal Multi-Revoluation Continuous Thust Orbit Transfers. Proceedings of the 26th Annual AAS/AIAA Astrodynamics Specialist Conference,Vail,CO.

1Texas A&M University,College Station,TX,USA.