多电平双丫移30°永磁同步电机的矢量控制系统

卢 峥 欧阳红林 孟 超 朱思国



多电平双丫移30°永磁同步电机的矢量控制系统

卢 峥1,2欧阳红林1孟 超1朱思国3

（1. 湖南大学电气与信息工程学院 长沙 410082 2. 南阳理工学院电子与电气工程学院 南阳 473000 3. 国网湖南省电力公司防灾减灾中心 长沙 410000）

为了进一步提高调速系统的容量，降低输出谐波和转矩脉动，将多电平逆变器与多相电机相结合，给出了五级十一电平级联型多电平逆变器驱动双移30°永磁同步电机的六相调速系统拓扑结构，分析了电压空间矢量在各正交空间的分布，研究了基于双级联型逆变器的四矢量空间矢量脉宽调制（SVPWM）算法。基于Matlab的仿真将级联型多电平逆变器驱动的双移30°永磁同步电机矢量控制系统与两电平逆变器驱动的双移30°永磁同步电机矢量控制系统进行比较，前者的转矩、稳态电流等性能均优于后者，其稳态电流总谐波畸变率仅为2.68%。基于DSP的实验表明级联型多电平逆变器输出波形接近正弦波，转矩脉动较小，稳态电流谐波含量低，达到了预期的控制效果，从而验证了本文所提方法的可行性。

级联型多电平逆变器 双移30°永磁同步电机 电压空间矢量控制

0 引言

多相电机由于具有可低压实现大功率、谐波含量低、转矩脉动小、容错能力强、比三相电机具有更多的控制自由度等优点受到了国内外专家学者的广泛关注，尤其是在大功率、高可靠性和低压供电的场合，如航天航空、舰船推进、核电站循环水系统等领域，多相电机具有不可替代的地位。随着调速系统容量的不断提高，多相电机的电压等级已达到6kV、10kV甚至更高，此时由于直流电压有限，传统的两电平逆变器驱动系统已不能满足需要，必须采用输出电压等级更高的多电平逆变器驱动。

多电平逆变器具有输出电平数高、输出波形接近正弦波、谐波含量少和电压变化率小等特点，因此适用于高压大功率应用场合，在大型工业生产如轧钢、造纸、水泥、煤炭、铁路、船舶等领域及综合潮流控制器（Unified Power Flow Controller, UPFC）和电力有源滤波器（Active Power Filter, APF）中得到了广泛应用[1]。常用的多电平逆变器电路拓扑结构有二极管钳位型[2-5]、飞跨电容型[6]和H桥级联型[7-9]。其中H桥级联型采用由独立直流电源供电的H桥基本功率单元进行叠加，不存在直流电容均压问题，具有所需元器件少、输出电压谐波含量少、易实现模块化和易扩展等优点。

传统相邻两矢量SVPWM算法只考虑ab平面上的正弦电压，而忽略了12平面上的谐波电压，因而存在较大的谐波损耗[10]。文献[11]针对电压源逆变器供电的双三相交流电机存在谐波电流的缺点，采用相邻四矢量合成参考矢量的SVPWM方法，有效地降低了谐波电流，并对开关序列进行了优化。但该方法采用的是两电平逆变器驱动，其输出的电压等级有限，电机转矩脉动大且稳态电流谐波含量大。为了进一步减小定子谐波电流，便于数字实现，文献[12]将六相电压源逆变器驱动双定子绕组感应电机的电压空间矢量划分为24个扇区，采用三个大矢量和一个中矢量合成参考电压的SVPWM方法，根据零矢量在开关周期中的位置将调制算法分为连续调制和非连续调制，经过分析比较得到连续调制适合中低压应用，而非连续调制适合高压应用的结论。但该方法并没有开展降低谐波损耗的分析，其降低谐波损耗的性能有待考证。文献[13]利用调整六相电压源逆变器中不同类型零矢量在开关周期中的作用时间，对相邻四矢量SVPWM算法进行优化，得到了不同调制度下理想的谐波特性，有效降低了逆变器的开关损耗。但该方法只对六相逆变器的SVPWM法进行了优化，并没有对六相逆变器驱动下多相电机的性能进行研究。以上方法都集中于两电平逆变器驱动多相电机的SVPWM算法，在直流母线电压一定的情况下，当调速系统容量更大，要求输出谐波更低时，两电平逆变器调速系统很难满足需要。而多电平逆变器的输出电压取决于多个直流电源串联的电压之和，可以方便地提高输出电压等级，从而提高调速系统的容量。另外，由于增加了电平数量，减小了输出电压的谐波，进一步减小了电机转矩的脉动，使调速系统具有良好的稳态性能，同时可减小逆变器中开关器件的耐压值和电压变化率，从而减小系统的电磁干扰。

1 多电平逆变器双丫 移30°PMSM空间矢量分布

图1 基于级联型H桥的多相电机拓扑结构

（1）

（3）

（5）

（6）

（8）

（9）

式（4）～式（9）得到的是六相静止坐标系下不同相电压的表达式，对其进行Park变换，将这些电压分别投影到三个彼此正交的子平面ab平面、12平面和12平面。其中电压矢量在ab平面和在12平面上的分布情况相同，在12平面上的分布为零。图2为电压矢量在ab平面的投影。FDBECA各相的开关模式用11进制数表示，其中0代表该相开关器件开关函数为-5, 1代表该相开关器件开关函数为-4，以此类推，11代表该相开关器件开关函数为5，六相一共有116=1 771 561种开关模式。其对应的电压空间矢量除去零矢量，按幅值大小可分为4 033组，分别为0.002 39、0.004 62、0.006 54、0.006 96、0.008、0.008 93、0.009 25、…、0.662、0.662 9、0.625 57、0.626 7、0.63、0.636 19、0.643 95。从图2中可以看出，六相逆变器输出电压矢量非常复杂，仅零矢量就有121个。

（a）电压矢量分布全貌

（b）电压矢量第一象限分布

图2 不同开关模式在ab平面上的投影

Fig.2 The mapping of different switching mode onabplane

2 双丫 移30°PMSM SVPWM调制算法

相对于传统的错位移相SPWM算法，SVPWM算法可提高逆变器15%的直流电压利用率，并能减小开关损耗，随着逆变器输出电压矢量的增多，采用SVPWM算法的调速系统可以使电机的磁链更接近圆形，不仅能提升电机的动态性能，还可以减小转矩的脉动。采用五级十一电平逆变器供电的双移30° PMSM共有1 771 561种电压矢量，通过坐标变换将这些电压矢量投影到彼此正交的ab、12、12坐标系，其中ab平面与机电能量转换有关，12平面只与谐波部分有关，电压矢量在12平面上的投影为零。从图2不同开关模式在ab平面上的投影情况看，最大幅值为0.643 95的矢量共有12个，这12个最大幅值的矢量将ab平面平分为12个扇区，如图3所示，而这些最大幅值的矢量在12平面上却是最小的[14]，因此可选用在ab平面幅值大且在12平面投影小的矢量对参考矢量进行合成。四矢量电压空间矢量调制方法是在常规空间矢量调制由两个基本矢量合成参考矢量的基础上增加两个电压矢量，以抵消电压矢量在12平面上产生的效果。为了减小逆变器的开关损耗，这里选用相邻最大四矢量法对参考矢量进行合成。

图3 最大幅值矢量在不同平面上的分布

文献[15]提出了一种应用于六相感应电机的电压源逆变器SVPWM调制方法，将六相逆变器分解成两个错开30°的三相逆变器分别进行控制，本文将其推广应用于双移30°永磁同步电机。将图1中A、C、E三相视为逆变器1，B、D、F三相视为逆变器2，后者在相位上滞后前者30°。当逆变器采用五级十一电平级联型结构时，每个逆变器的开关状态形成一个正六边形，两个逆变器形成的正六边形错开30°，它们的顶点在ab平面上形成一个正十二边形，整个平面被分成十二个扇区，如图4a所示。图4a中粗线代表逆变器1形成的正六边形，细线代表逆变器2形成的正六边形。第一象限对应的开关状态如图4b所示，当参考矢量位于图中所示位置时，根据其幅值的大小，可由相邻的四个基本矢量即逆变器1的（6,6,0）、（6,0,0）和逆变器2的（6,6,0）、（6,0,0）与零矢量合成，这就是基于双逆变器的四矢量SVPWM调制方法。其具体步骤如下：

（1）扇区判断。

（2）冗余矢量选择，确定合成参考矢量的四个电压矢量。

（3）计算四个电压矢量和零矢量的作用时间。

（4）合理选择零矢量，确定功率开关作用顺序，生成PWM波。

（a）双逆变器电压空间矢量形成的正十二边形

（b）第一区间详图

图4 双逆变器电压空间矢量图

Fig.4 The voltage space vector diagram of double inverters

2.1 扇区判断

文献[16]给出了五相永磁同步电机SVPWM扇区判断的方法，本文将其推广应用到双移30°永磁同步电机的SVPWM中。该方法无须转子磁极位置角的三角函数运算，只需对参考电压的a分量和b分量进行简单的算数与逻辑运算，就可以判断出参考电压所在的扇区，判断过程简单、易于实现。其具体过程如下。

定义6个变量

令

则扇区和之间的关系见表1。

表1 扇区判断对应关系

Tab.1 The corresponding relation of sector judgment

2.2 冗余矢量选择

扇区判断后需要根据参考矢量的幅值选择合成它的四个基本矢量，如上文所述，5级6相级联型逆变器共产生1 771 561种开关模式，存在大量的冗余矢量，这些开关状态的幅值最小为零，最大为0.643 95，将最大幅值平均分成11等份，每份为0.058 54，称为1阶，参考矢量幅值包含几阶，就由该阶对应的矢量合成参考矢量，具体由哪四个基本矢量合成需要根据参考矢量所在扇区决定。设参考矢量幅值包含阶，则基本矢量的选择见表2。

表2 基本矢量的选择

Tab.2 The table of selection of base vectors

2.3 作用时间的计算

每个采样周期中四个基本矢量和零矢量的作用时间计算式为

（12）

表3 电压矢量开关时间表

Tab.3 The switching time table of voltage vector

2.4 确定功率开关作用顺序

功率开关的作用顺序可以有多种选择，在每个采样周期内应尽可能少地进行功率开关切换，同时保持波形对称，这里采用离散调制方式，以图4b为例，当参考矢量位于第一象限第六阶时，应由逆变器2的开关状态（6,0,0）、逆变器1的开关状态（6,0,0）、逆变器2的开关状态（6,6,0）、逆变器1的开关状态（6,6,0）和零矢量合成。为了实现在扇区切换过程中矢量的平稳过渡，可使每个采样周期开关序列以（0,0,0）为首发矢量和末发矢量，这样有利于各个扇区的矢量平稳过渡，避免在参考矢量切换扇区时可能出现矢量突变问题。考虑冗余矢量选择和扇区过渡及各开关矢量的作用时间，其开关作用序列如图5所示。

图5 离散方式开关序列

2.5 谐波损耗分析

采用相邻最大四矢量SVPWM法比传统两矢量SVPWM法产生的谐波损耗小，下面通过分析计算进行证明。

在载波频率远大于基波频率的情况下可认为负载为纯感性，此时谐波磁链轨迹和谐波电流轨迹之间只存在一个比例系数。那么在一个载波周期中谐波磁链为

设载波周期为c，则谐波磁链在12平面上的瞬时值为

谐波磁链在12平面上的有效值为

由于参考矢量是由选定的电压矢量作用一定时间合成的，所以根据式（14）可确定其在12平面上的谐波磁链轨迹，然后根据式（15）计算各电压矢量在12平面上的谐波磁链有效值。电压矢量的不同作用顺序会对谐波磁链的轨迹产生一定的影响，这里选择开关损耗最小的电压矢量开关顺序。同时，当采用不同开关序列时，谐波磁链有效值也会不同，但对相邻四矢量SVPWM法与两矢量SVPWM法产生的谐波磁链有效值大小并无影响[17]。

本文选取逆变器2（6,0,0）、逆变器1（6,0,0）、逆变器2（6,6,0）、逆变器1（6,6,0）对应的四矢量合成参考矢量与逆变器1（6,6,0）与逆变器2（6,6,0）对应的两矢量合成参考矢量的谐波轨迹与谐波磁链有效值进行比较，根据式（14）计算得到四矢量和两矢量分别在12平面上的谐波磁链轨迹如图6所示。再根据式（15）计算出两者在12平面上的谐波磁链有效值分别为0.000 341 93和0.000 861 57，由此可以证明采用四矢量SVPWM法可以有效减小电压空间矢量在12平面上产生的谐波损耗。

（a）四矢量在12平面上的谐波磁链轨迹

（b）两矢量在12平面上的谐波磁链轨迹

图6 四矢量和两矢量在12平面上的谐波磁链轨迹

Fig.6 Harmonic flux trajectories of four vectors and two vectors on12plane

3 仿真与实验

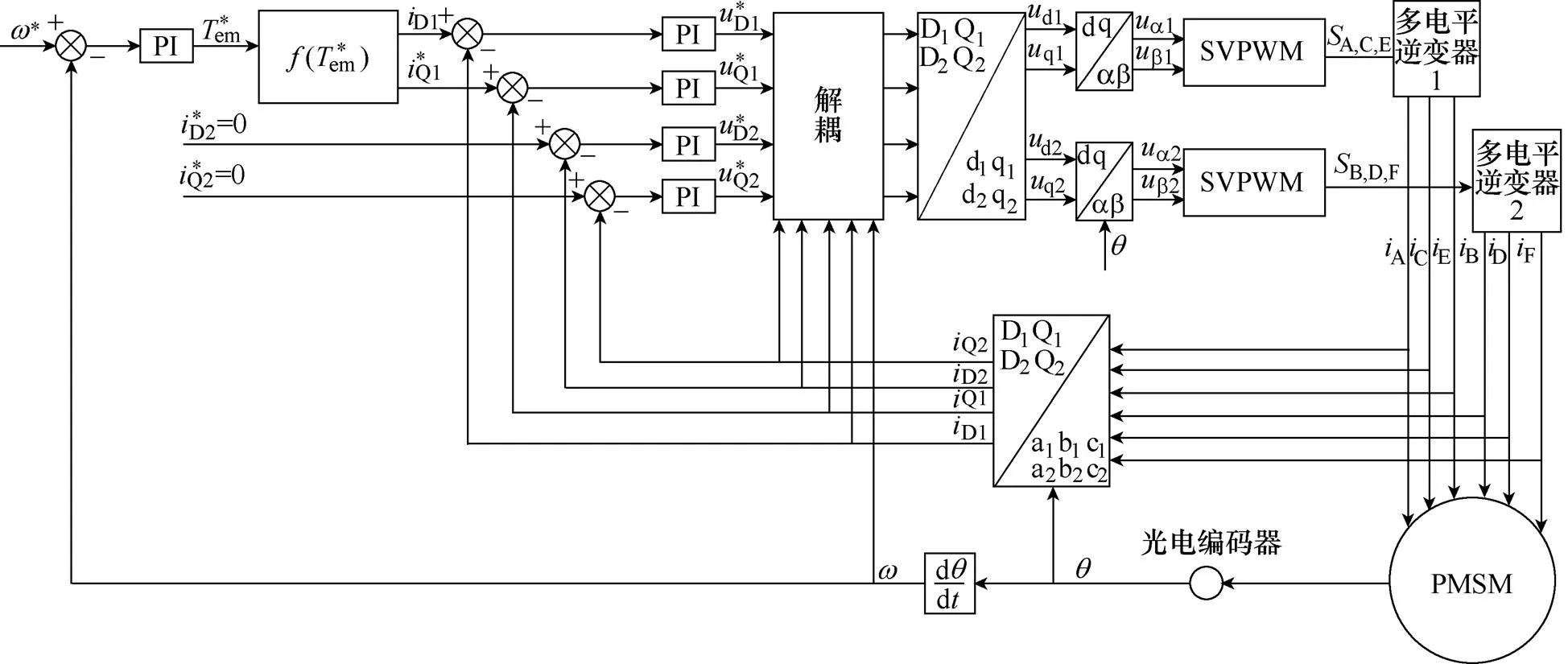
图7 基于多电平逆变器的双移30°PMSM矢量控制系统

图7中转速给定值与实际转速比较后经PI调节输出电磁转矩参考值，永磁同步电机dq坐标系下电磁转矩方程为

式中，em为电磁转矩；p为电机极对数；f为磁体磁链；d、q分别为电感在dq坐标系的d轴分量和q轴分量；d、q分别为电流在dq坐标系的d轴分量和q轴分量。据此可得电流参考矢量的两个分量和，这里采用的控制方式，即令=0，即可根据式（16）得到的值。四路电流参考值和从电机定子侧采样得到的电流经三相静止坐标向两相旋转坐标变换后的电流进行比较，经PI调节输出四路电压参考值。由于定子电压的D轴分量D1、D2和Q轴分量Q1、Q2之间存在耦合关系，所以对其进行解耦，得

式中，为电机角速度；D1、D2和Q1、Q2分别为电感在D1Q1和D2Q2坐标系的D轴分量和Q轴分量。由于本文采用的是两个多电平逆变器分别进行调制，需要将D1Q1和D2Q2坐标系的电压空间矢量D1、Q1和D2、Q2转换为传统的dq坐标系的电压矢量d1、q1和d2、q2，其转换方程为

（18）

再将得到的dq坐标系电压矢量分别进行两相旋转到两相静止坐标系的转换，即可得到SVPWM算法所需要的参考电压，采用上文所提的SVPWM调制算法分别给多电平逆变器1和多电平逆变器2发送触发脉冲，则两个逆变器分别输出A、C、E和B、D、F相电压，从而驱动双移30°PMSM进行调速。

为了方便分析，仿真和实验的参数一致。多电平逆变器采用由IGBT组成逆变单元的五级级联型结构，每个逆变单元由50V直流电源供电，调速系统采样频率为5kHz。双移30°永磁同步电机参数见表4。

表4 双移30°永磁同步电机参数

Tab.4 The parameters of double star winding shifted by 30°PMSM

（a）两电平逆变器输出线电压AC波形

（b）两电平逆变器输出线电压BD波形

（c）两电平逆变器输出线电压谐波分析

（d）两电平双移30°PMSM调速系统转矩波形

（e）两电平双移30°PMSM调速系统稳态电流波形

（f）两电平双移30°PMSM调速系统稳态电流谐波分析

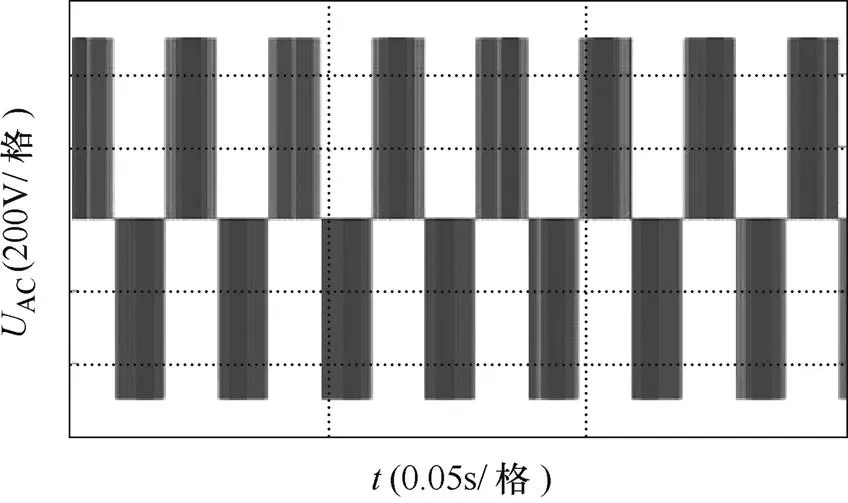
（g）多电平逆变器输出线电压AC波形

（h）多电平逆变器输出线电压BD波形

（i）多电平逆变器输出线电压谐波分析

（j）多电平双移30°PMSM调速系统转矩波形

（k）多电平双移30°PMSM调速系统稳态电流波形

（l）多电平双移30°PMSM调速系统稳态电流谐波分析

图8 仿真波形

Fig.8 The simulation waveforms

图9为基于TMS320F28335DSP搭建的基于多电平逆变器的双移30°永磁同步电机低压实验平台所测波形，图9a、图9b分别为两电平逆变器和多电平逆变器输出的AC线电压的波形，两者都为逆变器直流电压叠加的结果，在输出线电压幅值相同的情况下，两电平逆变器需要的直流电压为十一电平逆变器的10倍，反之，在直流电压相同的情况下，十一电平逆变器较两电平逆变器输出电压可提高10倍，且与仿真波形一致，后者呈现了较好的正弦性。图9c、图9d分别为两种调速系统输出的转矩波形，从图中可以看出多电平双移30°PMSM调速系统的转矩脉动比两电平双移30°PMSM调速系统小。这主要是因为多电平逆变器输出电压波形接近正弦波，谐波含量小，因此加在电机上产生的转矩脉动也小。图9e、图9f分别为两种调速系统稳态电流波形，同样因为逆变器输出电压谐波含量低，因此多电平双移30°PMSM调速系统的稳态电流波形畸变小，具有较好的稳态性能。

（a）两电平逆变器输出线电压AC

（b）多电平逆变器输出线电压AC

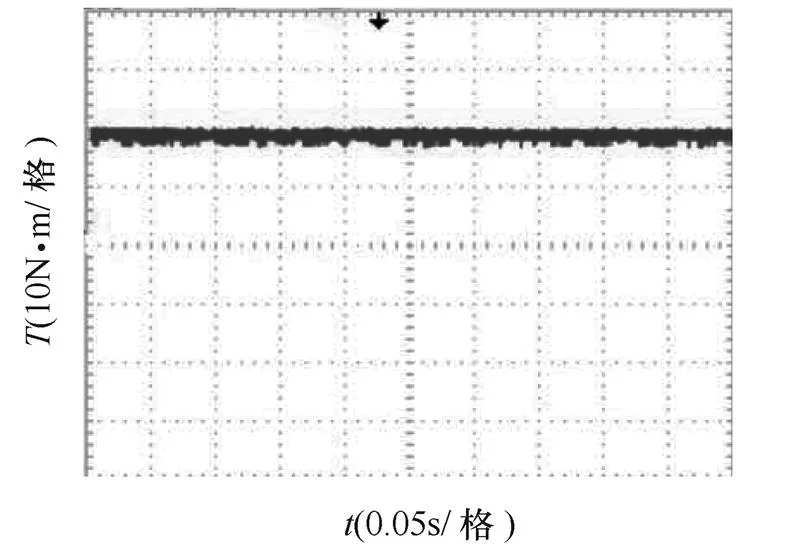
（c）两电平双移30°PMSM调速系统转矩波形

（d）多电平双移30°PMSM调速系统转矩波形

（e）两电平双移30°PMSM调速系统稳态电流波形

（f）多电平双移30°PMSM调速系统稳态电流

图9 实验波形

Fig.9 The experimental waveforms

4 结论

参考文献：

[1] 刘凤君. 多电平逆变技术及其应用[M]. 北京: 机械工业出版社, 2007.

[2] 高跃, 李永东. 二极管钳位型五电平逆变器电容电压平衡域研究[J]. 电工技术学报, 2008, 23(1): 77-83.

Gao Yue, Li Yongdong. Voltage balance boundary of five-level diode clamped inverters[J]. Transactions of China Electrotechnical Society, 2008, 23(1): 77-83.

[3] 姜卫东, 王群京, 陈权, 等. 二极管钳位型多电平逆变器全范围电容电压平衡的PWM调制方法[J].中国电机工程学报, 2009, 29(15): 28-35.

Jiang Weidong, Wang Qunjing, Chen Quan, et al. PWM algorithm for diode clamped multi-level voltage source inverter with capacitor voltage balance under full condition[J]. Proceedings of the CSEE, 2009, 29(15): 28-35.

[4] 吴可丽, 夏长亮, 张云, 等. 二极管钳位型三电平逆变器共模电压抑制[J]. 电工技术学报, 2015, 30(24): 110-117, 170.

Wu Keli, Xia Changliang, Zhang Yun, et al. Common-mode voltage suppression for neutral-point- clamped three-level inverter[J]. Transactions of China Electrotechnical Society, 2015, 30(24): 110- 117, 170.

[5] 刘云峰, 何英杰, 陈娟, 等. 二极管钳位多电平空间矢量与载波调制策略统一理论研究[J]. 中国电机工程学报, 2015, 35(5): 1203-1210.

Liu Yunfeng, He Yingjie, Chen Juan, et al. Research of the unity theory between space vector and carrier-based PWM modulation strategy in diode clamped multilevel inverters[J]. Proceedings of the CSEE, 2015, 35(5): 1203-1210.

[6] 王鸿雁, 王小峰, 张超, 等. 飞跨电容多电平逆变器的新型载波PWM方法[J]. 电工技术学报, 2006, 21(2): 63-67, 92.

Wang Hongyan, Wang Xiaofeng, Zhang Chao, et al. Carrier-based PWM method with voltage balance for flying capacitor multilevel inverter[J]. Transactions of China Electrotechnical Society, 2006, 21(2): 63-67, 92.

[7] 李继华, 阮新波, 王学华. 级联型多电平逆变器线电压谐波优化的SVPWM策略[J]. 电工技术学报, 2014, 29(6): 120-128.

Li Jihua, Ruan Xinbo, Wang Xuehua. A SVPWM strategy with optimal line-to-line voltage harmoni- cspectrum for cascaded multilevel inverters[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 120-128.

[8] 李宇飞, 王跃, 吴金龙, 等. 级联H桥变流器的波动电压生成控制策略[J]. 电工技术学报, 2015, 30(9): 46-52.

Li Yufei, Wang Yue, Wu Jinlong, et al. Control strategy for fluctuating voltage generation in cascaded H-bridge converters[J]. Transactions of China Electrotechnical Society, 2015, 30(9): 46-52.

[9] 蔡信健, 吴振兴, 孙乐, 等. 直流电压不均衡的级联H桥多电平变频器载波移相PWM调制策略的设计[J]. 电工技术学报, 2016, 31(1): 119-127.

Cai Xinjian, Wu Zhenxing, Sun Le, et al. Design for phase-shifted carrier pulse width modulation of cascaded H-bridge multi-level inverters with non- equal DC voltages[J]. Transactions of China Elec- trotechnical Society, 2016, 31(1): 119-127.

[10] 杨金波, 杨贵杰, 李铁才. 六相电压源逆变器PWM算法[J]. 电工技术学报, 2012, 27(7): 205-211.

Yang Jinbo, Yang Guijie, Li Tiecai. PWM techniques for six-phase voltage-source inverters[J]. Transa- ctions of China Electrotechnical Society, 2012, 27(7): 205-211.

[11] Djafar Hadiouche, Lotfi Baghli, Abderrezak Rezzoug. Space-vector PWM techniques for dual three-phase AC machine: analysis, performance evaluation, and DSP implementation[J]. IEEE Transactions on Industry Applications, 2006, 42(4): 1112-1122.

[12] Khoudir Marouani, Lotfi Baghli, Djafar Hadiouche, et al. A new PWM strategy based on a 24-sector vector space decomposition for a six-phase VSI-fed dual stator induction motor[J]. IEEE Transactions on Industrial Electronics, 2008, 55(5): 1910-1920.

[13] 付胜杰, 彭侠夫. 六相逆变器空间矢量脉宽调制策略的分析与优化[J]. 哈尔滨工程大学学报, 2012, 33(4): 512-516.

Fu Shengjie, Peng Xiafu. Analysis and optimization of SVPWM strategy for a six-phase inverter[J]. Journal of Harbin Engineering University, 2012, 33(4): 512-516.

[14] 孟超. 双三相永磁同步电机驱动系统的研究[D]. 长沙: 湖南大学, 2011.

[15] 侯立军, 苏彦民, 陈林. 一种新颖的用于六相感应电机调速系统的空间矢量PWM方法[J]. 电工电能新技术, 2004, 23(1): 11-15.

Hou Lijun, Su Yanmin, Chen Lin. A novel space vector PWM method for six-phase induction machines[J]. Advanced Technology of Electrical Engineering and Energy, 2004, 23(1): 11-15.

[16] 姜海博, 黄进, 康敏. 单绕组五相永磁无轴承电机的SVPWM控制[J]. 电工技术学报, 2011, 26(1): 34- 39.

Jiang Haibo, Huang Jin, Kang Min. SVPWM control for a 5-phase PM bearingless motor with single set of windings[J]. Transactions of China Electrotechnical Society, 2011, 26(1): 34-39.

[17] 孟超, 欧阳红林, 刘鼎, 等. 基于模糊逻辑和重构电压矢量的双移30°PMSM直接转矩控制[J]. 中国电机工程学报, 2011, 31(24): 59-67.

Meng Chao, Ouyang Honglin, Liu Ding, et al. Direct torque control for dual Y shift 30 degree permanent- magnet synchronous motor based on fuzzy logic and rebuilding voltage vector[J]. Proceedings of the CSEE, 2011, 31(24): 59-67.

[18] Jussi Karttunen, Samuli Kallio, Pasi Peltoniemi, et al. Decoupled vector control schemefor dual three- phase permanentmagnet synchronous machines[J]. IEEE Transactions on Industrial Electronics, 2014, 61(5): 2185-2196.

Vector Control System of Multilevel Inverter Double Star Winding Shifted by 30°Permanent Magnet Synchronous Motor

1,2113

（1. College of Electrical Engineering Hunan University Changsha 410082 China 2. School of Electronic and Electrical Engineering Nanyang Institute of Technology Nanyang 473000 China 3. State Grid Hunan Electric Company Disaster Prevention and Reduction Center Changsha 410000 China）

In order to further improve the capacity of the speed regulating system and reduce the output harmonic and torque ripple, this paper applies the multilevel inverter technology in multiphase machine. The speed regulating system with 30°-shift double-star winding of permanent magnet synchronous motor (PMSM) is provided, which is fed by eleven-level cascaded multilevel inverter. The distributions of voltage space vectors in different orthogonal spaces are analyzed in detail. Meanwhile, the four-vector space vector pulse width modulation (SVPWM) algorithm is presented based on two cascaded inverters. In Matlab simulation, the PMSM vector control system of 30°-shift double-star winding driven by the multilevel inverter is compared with the vector control system supplied with the two-level inverter. Regarding the former control system, its performance of torque and steady current is superior to the latter, and the total harmonics distortion (THD) of steady current is only 2.68%. The experimental results based on DSP show that the output waveforms of cascaded multilevel inverter are close to sinusoidal wave. Besides, the ripples of the torque are small and the harmonic content of steady current is low. It has reached the expected control effect, which verifies the feasibility of the proposed method.

Cascaded multilevel inverter, permanent magnet synchronous motor of 30°-shift double-star winding, voltage space vector control

TM464

国家自然科学基金资助项目（51237003、51677063）。

2016-01-29 改稿日期 2016-03-29

卢 峥 女，1978年生，博士研究生，研究方向为电力电子与电力传动和多相电机的驱动控制。E-mail: lucia106@163.com（通信作者）

欧阳红林 男，1965年生，博士，教授，研究方向为电力电子与电力传动、多相电机系统及其控制。E-mail: oyhl1405.ouyang@vip.sina.com