水平轴潮流能水力涡轮数值模拟与试验研究

肖云峰，高鹏远，黄俊强，王　信，邹文昊

（1.北京石油化工学院，北京　102617；2.北京化工大学，北京　100029）

水平轴潮流能水力涡轮数值模拟与试验研究

肖云峰1，高鹏远2，黄俊强1，王信1，邹文昊1

（1.北京石油化工学院，北京102617；2.北京化工大学，北京100029）

首先，使用叶素动量理论对所设计的室内试验用小型水平轴潮流能水力涡轮叶片模型进行初步计算，获得其性能参数，此后借助NUMECA软件，采用三维计算流体动力学(CFD)方法对水平轴水力涡轮进行三维水动力分析，得到其性能曲线，最后通过试验水槽进行模型试验，对BEM计算结果和CFD计算结果进行验证，结果表明：叶素动量理论和CFD方法均能对水力涡轮性能进行有效预测，且CFD方法具有更高的精度；此外，根据CFD方法得到叶片表明的压力分布，根据空化条件可知，该水力涡轮会发生空化。

BEM；CFD；水动力性能；空化；实验

21世纪以来，随着科技的发展和人口的增长，传统能源如煤、石油、天然气紧缺的问题日渐凸显。目前，我国石油消费量居世界第二，超过50%依赖进口。积极开发与研究新型能源，消除我国能源隐患，使能源结构合理化已经成为大势所趋[1]。潮流能作为一种新能源,具有蕴藏能量大、绿色环保的特点，在不占用陆地空间的同时，可以实现资源综合利用，这正好弥补了常规化石能源的不足之处。此外，随着化石能源等不可再生能源的日益减少以及对环境的保护要求越来越高，如何有效开发利用潮流能引起各国的高度重视。在海洋能的开发利用领域中，潮流能的开发利用已变得最为活跃[2]。

潮流能发电装置的核心装备为水力涡轮，其作用就是将海水的动能转化为叶轮的机械能，各国研究人员开发了多种不同形式水力涡轮。其中水平轴潮流能水力涡轮具有效率高、技术相对成熟的特点，同时可以借鉴水平轴风力机开发利用的经验，是具有较好应用前景的形式，在目前的潮流能开发装置中占到很大份额。笔者以自行设计的20 W潮流能水力涡轮为例，基于Qblade二维计算软件和NUMECA流体三维模拟软件，对所设计的叶片进行水动力性能计算，并将计算结果与实验结果进行对比。

1　理论基础

1.1叶素动量理论

当前国内外计算风力机叶片气动性能的理论有贝茨理论、动量理论、叶素理论、叶素动量理论[3-4]等。其中，叶素动量理论结合了动量理论和叶素理论，计算出风轮扫掠面中的迭代变量轴向诱导因子a和周向诱导因子b。如图1所示，风轮流动模型简化为一个理想的单元流管，并将其离散成N个高度为dr的环形单元，单元之间没有流动。

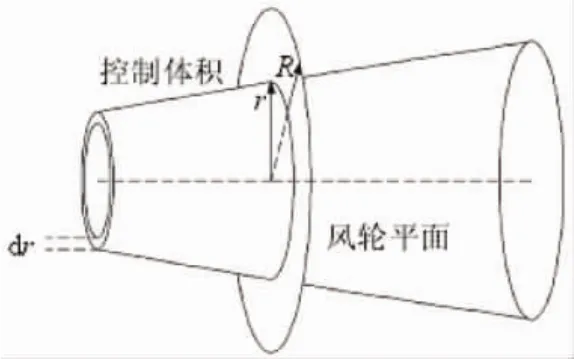
图1　叶素动量理论单元流管模型

由动量理论可得到作用在dr微段上的推力及转矩：

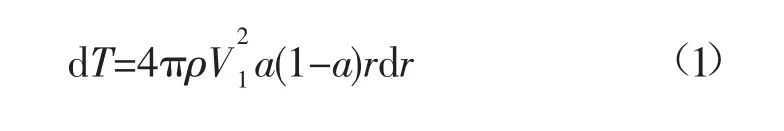
通过叶素理论可以得到作用在dr微段的推力与转矩：

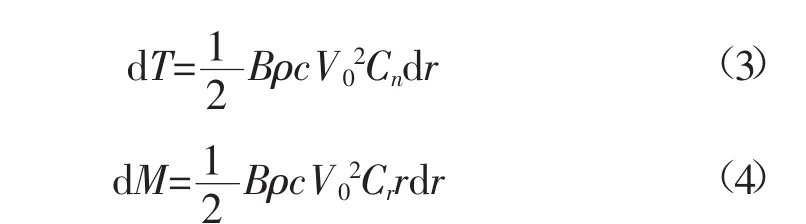
由叶素理论和动量理论得出的推力和转矩相等，并由速度三角形可得：

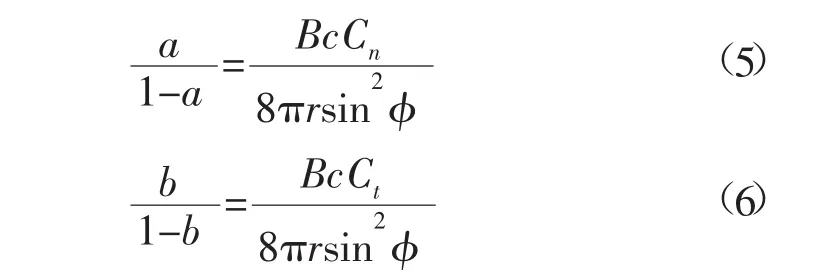
1.2CFD基本理论

NUMECA公司的FINE/TURBO软件包具有十分强大的流场计算和前后处理功能。FINE/TURBO采用时间相关法求解雷诺平均的N-S方程，离散方式为中心节点的有限体积法，以显示四阶RUNGEKutta法求解，并具有多重网格初场处理和多重网格迭代加速以及低流速的预处理技术。湍流模型为一方程Spalart-Allmaras（S-A）模型。

1.3叶片模型

水力涡轮为水平轴三叶片定桨型，叶片半径0.19 m，额定功率20 W，叶尖速比为3，设计流速为1 m/s，叶片旋转轴为Z轴。

图2　叶片模型

1.4计算域和网格

与风力机相同，水力涡轮计算域包括内部流动域和外部绕流域，计算域的精准程度关乎计算结果的准确程度，因此，必须严格把握计算域。根据水力涡轮实际工作情况确定计算区域包括叶片旋转平面，进口段和出口段，其中叶片展向延伸到3倍半径（3R），考虑到水力涡轮下游尾流的影响叶片下游尺寸为5倍叶高，上游也设定为5R。

计算网格通过Igg/AutoGrid模块生成，如图3所示，由于叶片流道具有周期性，因此只需给出单列网格。最终生成的网格单列网格总数约为83万，无负网格，流道最小网格正交性为16.149，远场最小网格正交性为 16.218，流道最大长宽比为767.39，远场为2 583.6，流道最大延展比2.976 4，远场为2.611 2。网格质量符合计算要求。

比如，2005年起，石化销售系统开始逐步实现增值税市级集中缴纳，因各市、区县财政收入不均衡，导致市级集中纳税多没有得到地方认可，所以部分公司一直按各自经营所在地收入比例在当地入库缴纳增值税，其中依此计算的城建税比例县区是5%、市区是7%，相差两个百分点，如果完全集中缴纳，这两个百分点的纳税幅度累积下来也是不小的开支。所以，涉及企业完全可以在税源不是十分紧张的情况下，利用各级税种的税负差别，逐渐减少或不实行集中纳税，放归税源所在地缴纳，如果有减免或税收优惠政策的，可加以利用集中缴纳，尽量把几个百分点的减税或增收作用利用起来。

图3　网格示意图

进口边界条件：给定水流轴向流速、静温以及湍流粘性。出口边界条件设定压力出口，轮毂可设定为Euler壁面，叶片表面设定为粘性壁面。当计算残差下降三个量级以上，总体性能参数达到稳定认为收敛。

2　结果讨论

2.1性能分析

根据CFD理论计算的额定工况下水力涡轮性能结果如图4所示，在叶尖速比为3时，叶片功率系数达到最大值0.353 471，略大于设计点。与BEM方法计算结果比较，获能系数和推力系数变化趋势基本一致，而获能系数曲线最高点左移，最大值有所下降，推力系数最大值也有所下降，这是因为叶素动量理论计算过程中忽略了叶尖损失、叶根损失等因素的影响。在叶尖速比为3时达到最大值，且获能系数均超过0.35，而当水流速度增大时，获能系数增大，因此在合理范围内增大流速会使水力涡轮的性能有所提升，这对水力涡轮在实际运用中有很好的指导作用。

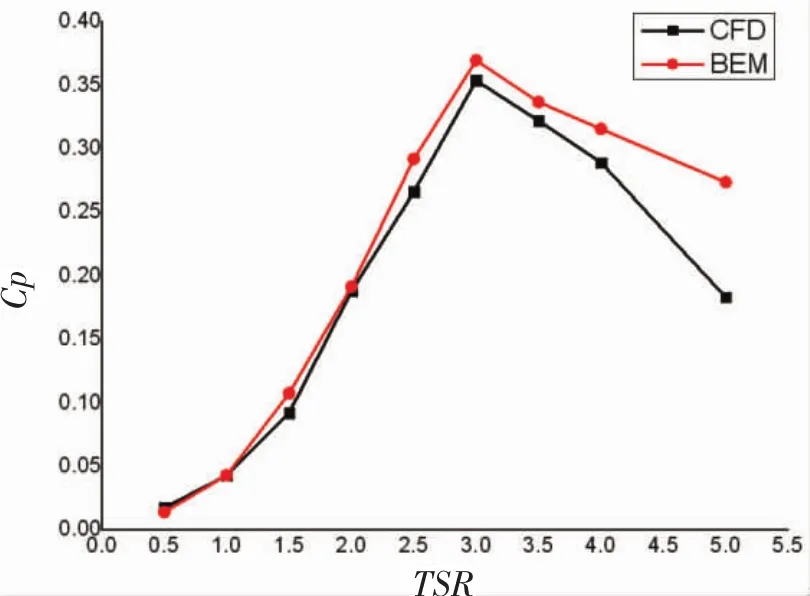
图4　额定工况下功率系数和推力系数随叶尖速比变化趋势

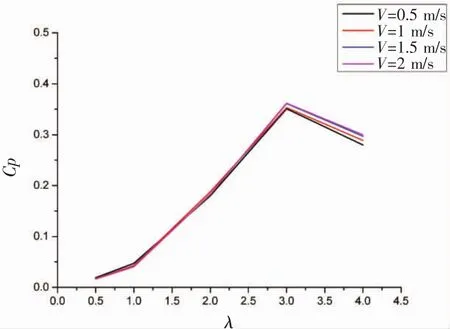
图5　不同流速下的功率系数

2.2空化分析

空化现象经常发生在水力涡轮运行过程中，空化的产生对水力涡轮性能产生严重影响[5]。空化是指水流冲击水力涡轮叶片时，叶片吸力面产生负压，低于一定压力（气化压力）时，叶片表面形成气泡，由于压力过低，气泡越来越大，气泡破裂后对叶片形成冲击，影响水力涡轮性能，由于累积作用，严重时会对水力涡轮叶片造成损坏，因此研究水力涡轮的空化十分必要。

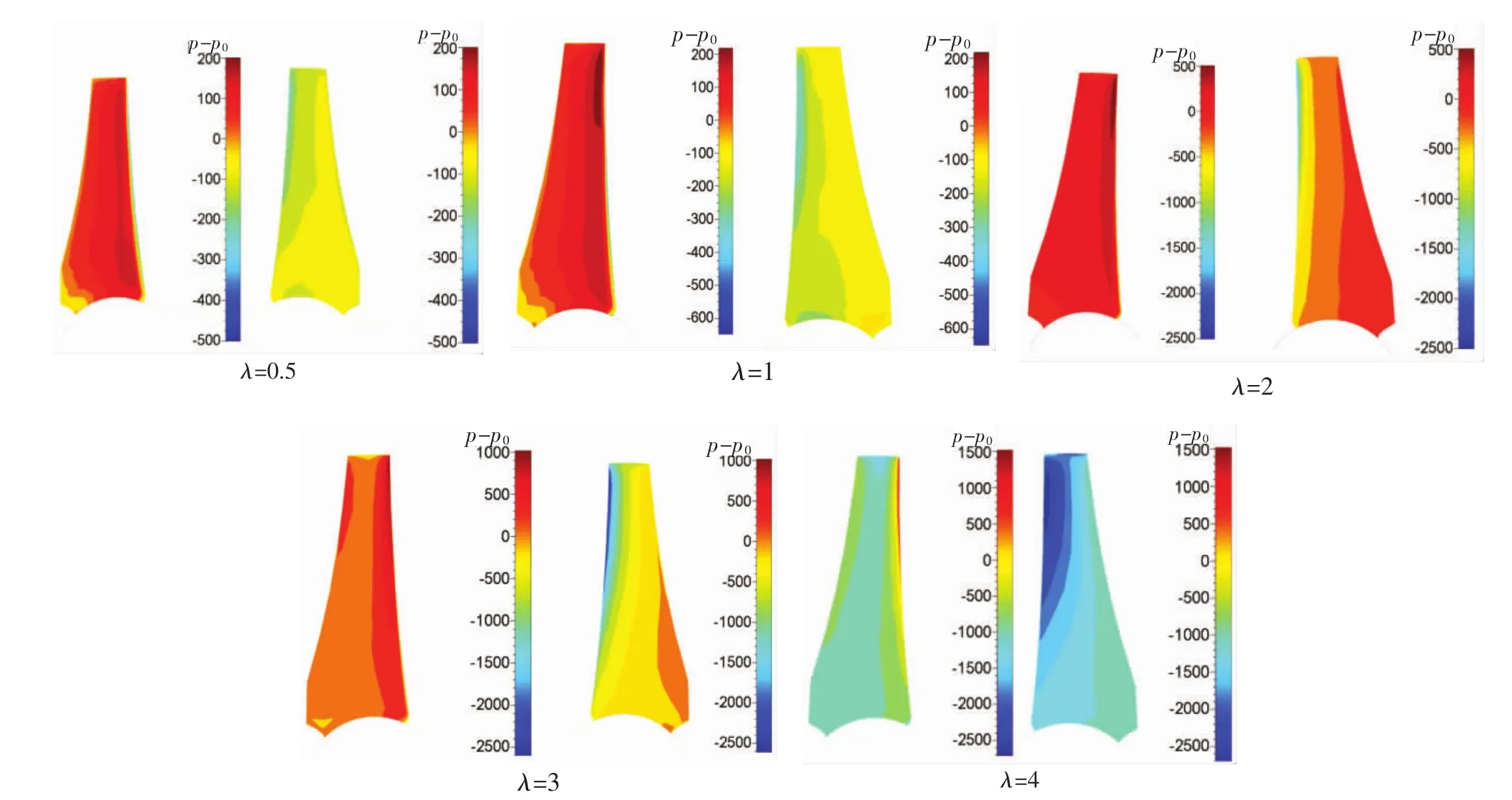
图6　不同叶尖速比下叶片表面压力分布

空化系数是用于判断空化是否发生的一个重要表征，对比叶片表面压力系数与空化系数的大小可以判断空化是否发生。空化数为：

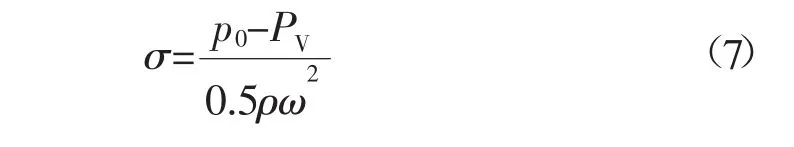
式中：p0为叶片截面静压；PV为水气化压力；

对比各截面压力与20℃水的气化压力值可知，各截面压力均小于水气化压力值，因此会发生空化，随着转速的增加，叶片最小压力值进一步减小，空化现象更加严重。因此对于控制叶片空化可以从降低转速入手[6-7]。

表1　不同尖速比下吸力面最低压强

表2　水在不同温度下的气化压力值

3　试验研究

根据设计叶片的具体参数，利用数控加工进行叶片制作。借助实验室自行搭建的敞开式试验水槽进行试验，试验仪器包括：水泵、变频器、扭矩传感器、发电机交直流功率测量仪以及流速测量仪[7]。

图8　试验水槽

图9　试验叶片

图10　试验过程

3.1叶片性能实验

叶片性能实验有两个目的：一是验证所设计的叶片性能是否满足要求；二是验证利用BEM方法和CFD方法计算结果的正确性。

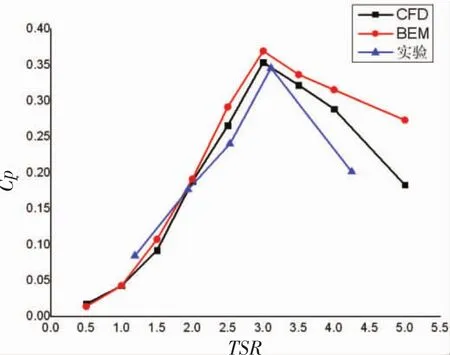
图11　水力涡轮性能曲线

图11为三叶片水力涡轮分别通过实验、BEM方法和CFD方法得到的性能曲线。由图11可知，BEM和CFD方法的计算值与试验值变化基本趋势一致；通过BEM和CFD方法得出的结果，在尖速比为3时功率系数取得最大值，其中CFD方法所得结果为0.353 47，BEM方法所得为0.369 31；而实验所得最大功率系数在叶尖速比为3.11处，功率系数为0.345 5，试验值与计算值接近；在叶尖速比为2～4之间，试验值比计算值小，这是由于计算选取较为理想的环境，忽略了叶尖以及叶根损失，同时，由于测量方法的局限性，实验中各种传动结构的能量损失也被计算在内，因此造成试验值相比计算值偏低。但是通过对比曲线可以看出，BEM方法和CFD方法都能作为预测水力涡轮性能的理论方法。

3.2不同叶片数水力涡轮性能实验

将叶片数增加至6，测得其性能，并与三叶片实验结果以及BEM方法的计算结果相对比。

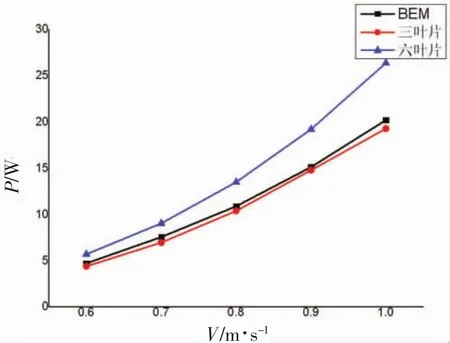
图12　不同叶片数功率随流速变化的曲线

从图12中可以看出：BEM方法对三叶片水力涡轮不同流速工况预测的值与试验结果变化趋势一致，实验值略小于计算值，原因如上节所描述，这是实验中的各种损失造成的；通过对比不同叶片数的功率曲线可以看出，叶片数的增多使得水力涡轮的整体获能性能上升，对于提高水力涡轮的性能有帮助。

4　结论

根据计算结果分析可得以下结论：

（1）采用BEM理论和三维CFD理论计算所得的水力涡轮叶片功率曲线与实验所得结果变化趋势基本一致。BEM方法和CFD方法均能作为水力涡轮性能预测的理论方法。

（2）BEM方法计算所得结果相比CFD方法计算结果偏大，这是由于BEM方法忽略了叶尖损失和叶根损失的影响，但是其计算速度是CFD方法所不能比的。因此，BEM方法作为快速预测水力涡轮性能的方法是可取的。

（3）不同流速下水力涡轮性能基本保持一致，流速增大时，叶轮获能系数有所提高，因此在合理范围内增大水流速度对叶片性能有所提高。

（4）水力涡轮叶片会发生空化现象，叶尖区域相比叶根更容易发生空化，转速越高，空化现象越严重。因此，可以采用降低转速和加大叶片翼型的厚度和弯度方法，减少空化的发生。

[1]史丹,刘佳骏.我国海洋能源开发现状与政策建议[J].中国能源,2013,35(9):6-11.

[2]Fraenkel P.Tidal Current Energy Technologies[J].Marine Current Turbines Ltd.Ibis,2006,148:145-151.

[3]Noda M,Flay R G J.A Simulation Model for Wind Turbine Blade Fatigue Loads[J].Journal of Wind Engineering and Industrial Aerodynamics,1999,83(1/3):527-540.

[4]Maalawi K Y,Badawy M T S.A Direct Method for Evaluating Performance of Horizontal Axis Wind Turbines[J].Renewable& Sustainable Energy Reviews,2001,5(2):175-190.

[5]江帆，黄鹏.Fluent高级应用与实例分析[M].北京：清华大学出版社,2010.

[6]辛晓鹏.水平轴海流能发电机械水动力性能的研究[D].杭州：浙江大学,2010.

[7]应有,李伟,刘宏伟，等.海流能发电装置叶片性能及气蚀研究[J].风机技术—试验研究,2008,4:8-19.

[8]王俭超.水平轴潮流水轮机叶片设计和模型试验研究[D].青岛：中国海洋大学,2011.

Numerical Simulation and Experimental Study on a Horizontal Axis Tidal Current Hydraulic Turbine

XIAO Yun-feng1,GAO Peng-yuan2,HUANG Jun-qiang1,WANG Xin1,ZOU Wen-hao1
1.Beijing Institute of Petrochemical Technology,Beijing 102617,China; 1.Beijing University of Chemical Technology,Beijing 100029,China

This paper uses the blade momentum theory to calculate the parameters of a small-scale horizontal axis hydraulic turbine for laboratory test to obtain its performance.With the NUMECA software,the three-dimensional computational fluid dynamics(CFD)method is adopted for 3-D hydrodynamic analysis on the horizontal hydraulic turbine,so as to derive the power curve.Finally,a model experiment is carried out in the experimental water tank,and the results of BEM and CFD calculation are verified,showing that both the momentum theory and CFD method can effectively predict the performance of the hydraulic turbine,and the CFD method is more accurate.In addition,the pressure distribution of the blade is obtained through the CFD method.According to the cavitation conditions,cavitation can occur on the hydraulic turbine.

BEM;CFD;hydrodynamic performance;cavitation;experiments

P743；TK73

A

1003-2029（2016）05-0080-05

10.3969/j.issn.1003-2029.2016.05.016

2016-04-18

肖云峰（1976-），男，副教授，主要从事特种叶轮机械设计与研发。E-mail：xiaoyunfeng@bipt.edu.cn