等跨等截面桥梁顶推施工导梁参数分析

2016-12-12蹇钢陈常松

公路与汽运 2016年6期

关键词：导梁悬臂支点

蹇钢，陈常松

（长沙理工大学土木工程与建筑学院，湖南长沙 410004）

等跨等截面桥梁顶推施工导梁参数分析

蹇钢，陈常松

（长沙理工大学土木工程与建筑学院，湖南长沙 410004）

为减小顶推施工中梁体的内力，选取合适的导梁参数至关重要。文中根据连续梁顶推施工通常为等跨、等截面的特点，分析顶推过程中梁体内力的变化规律，利用结构力学力法中的三弯矩方程建立力学解析模型，计算和分析等跨等截面连续梁顶推施工过程中导梁刚度、长度和自重荷载集度对主梁内力的影响，得出等跨等截面连续梁顶推施工中主梁受力最不利位置，并对该位置受力进行分析，得到顶推施工中选取导梁最优设计参数的方法。

桥梁；顶推施工；导梁优化；三弯矩方程；参数分析

使用顶推工艺施工桥梁结构时，梁体悬臂端的支点弯矩与跨径的平方成正比，受主梁材料和截面形式等的限制，顶推跨径有一定限值。若要加大跨径，一方面可使用临时墩，另一方面可通过优化导梁来实现。考虑到顶推施工过程既要满足桥梁施工安全的要求，又要满足经济效应最大化的需要，设计及施工中都应使顶推过程中最大弯矩值相对较小。该文分析导梁设计刚度、长度及线荷载集度对顶推过程中主梁内力的影响，为顶推设计和施工提供参考。

1 顶推全过程力学模型

为了方便分析，作如下假定：1）导梁与钢主梁刚接，导梁-主梁作为一个整体结合在一起；2）导梁与主梁分别具有均一的自重荷载集度和刚度，导梁的自重荷载集度和刚度分别表示为qn、In，主梁的自重荷载集度和刚度分别表示为q、I；3）不考虑梁体沿下部支撑线形的切线方向分力，梁体的重量沿跨长均匀分布；4）忽略支座变形和其他环境因素及施工误差导致的结构次内力。以上假定均基于理想的顶推施工情况，可反映顶推过程中导梁各参数对主梁受力的影响趋势。

为了便于绘图和比较分析，以下各弯矩值均用无量纲的形式表示。分析中将导梁所在跨段称为顶推跨段，顶推跨段前进方向支撑点称为顶推跨前端支点，顶推跨段后方支点称为顶推跨后端支点。

将钢梁顶推施工过程划分为3个阶段：第一阶段为从导梁开始顶推到导梁前端抵达顶推跨前端支点，该阶段梁体处于单悬臂状态；第二阶段为导梁上顶推跨前端支点，随着梁体的顶推，导梁在顶推跨前端支点上滑行；第三阶段为导梁前端完全滑出顶推跨前端支点，主梁前端抵达顶推跨前端支点。设顶推桥跨跨径相等，均为l，钢导梁长度为ln，不断前进的主梁前端到顶推跨后端支点n的距离为x，则顶推第一阶段可表示为0≤x＜l-ln，顶推第二阶段可表示为l-ln≤x＜l，顶推第三阶段可表示为x =l。图1为顶推施工力学解析计算简图。

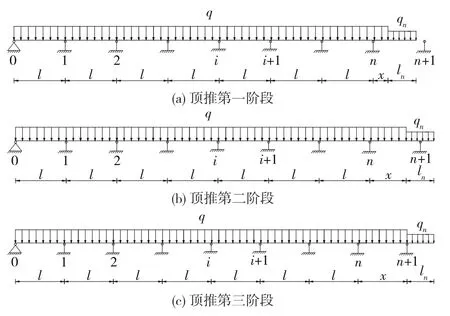
图1 顶推施工力学解析计算简图

2 顶推过程计算理论

在梁体顶推过程中，结构属于超静定体系。超静定体系的截面内力须综合平衡条件、几何条件、物理条件，根据求解计算途径的不同，采用力法（柔度法）和位移法（刚度法）及由此延伸出的混合法、弯矩分配法、矩阵位移法等进行求解。这里采用位移法。

2.1 顶推第一阶段弯矩求解

2.1.1 顶推跨后端支点n弯矩求解

在顶推开始时x=0，支撑截面n处的负弯矩值

Mn由悬出的导梁引起，其值为：

随着顶推的进行，Mn开始增大，其值为：

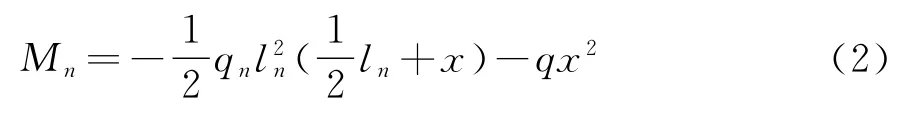
2.1.2 顶推中间跨支点弯矩求解

运用弯矩三弯矩方程和力的叠加原理对顶推中间支点进行求解。在解析计算中定义顶推进度与跨径之比α=x／l、导梁长度与跨径之比β=ln／l、导梁自重荷载集度与主梁自重荷载集度之比γ=qn／q、导梁刚度与主梁刚度之比η=EnIn／（EI）。根据上述基本假定及多余约束处的变形协调条件，得到连续梁三弯矩方程式为：

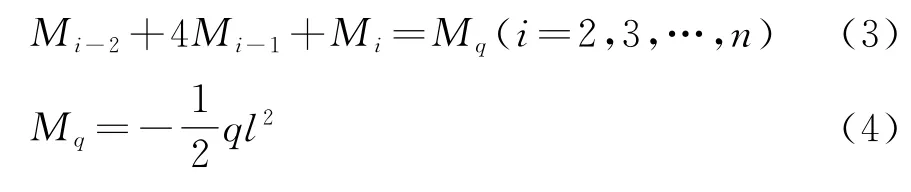
支点“0”处的弯矩值M0需根据顶推场地的具体情况确定，在后续计算中认为M0=0。

顶推第一阶段梁体处于单悬臂状态，支点n处的弯矩值只与主梁悬出长度相关，其值为：

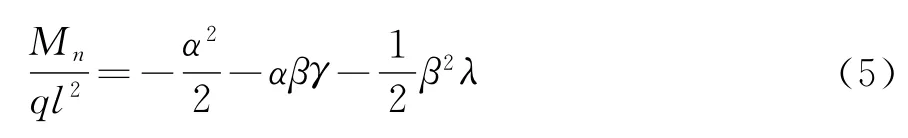
根据递推法由式（3）推导得：

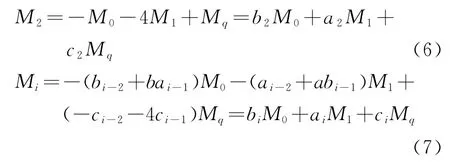
对于数列an｛｝、bn｛｝、cn｛｝，根据其初值及递推公式可得到通项公式：

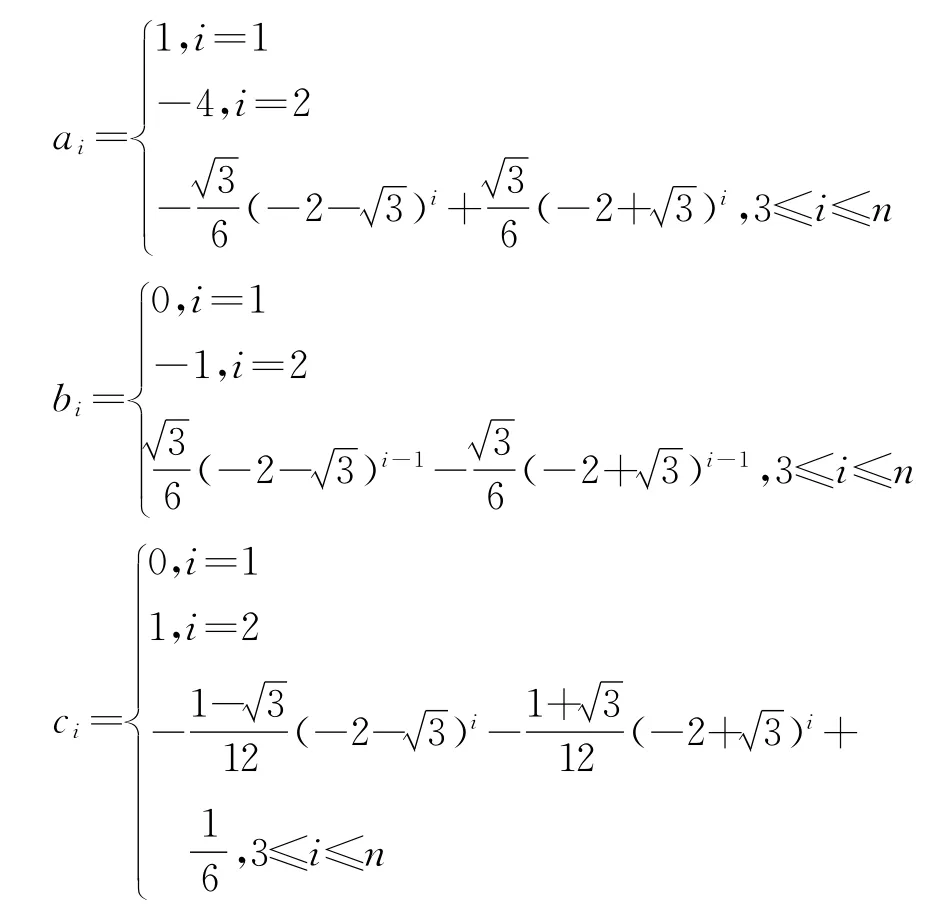
令式（7）中i=n，得：

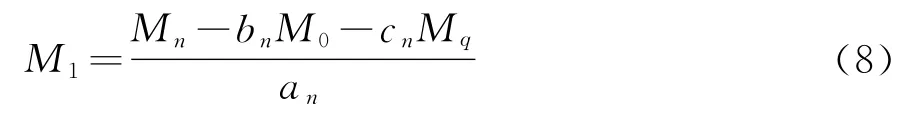
将式（8）代入式（7），得到等截面等跨连续梁各支点的弯矩值：

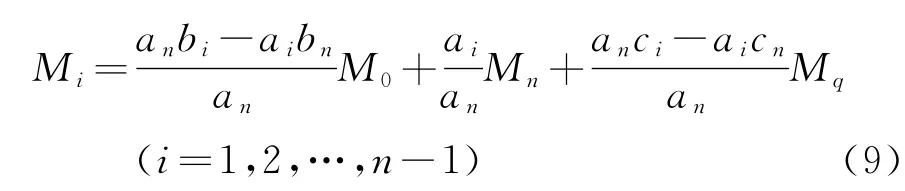
根据计算模型，可忽略M0的影响，即M0=0，则式（9）可简化为：

由上述分析可知，在导梁顶推的第一阶段主梁处于单悬臂状态，等截面连续梁中间跨支点的弯矩可分解为由悬臂端力矩引起的Mn和由梁体自重引起的Mq两部分。取连续梁跨数n为2～10，计算式（10）在不同跨数下的弯矩系数k1、k2（见表1、表2），从而得到连续梁中间支点的弯矩值与Mn、Mq的关系。

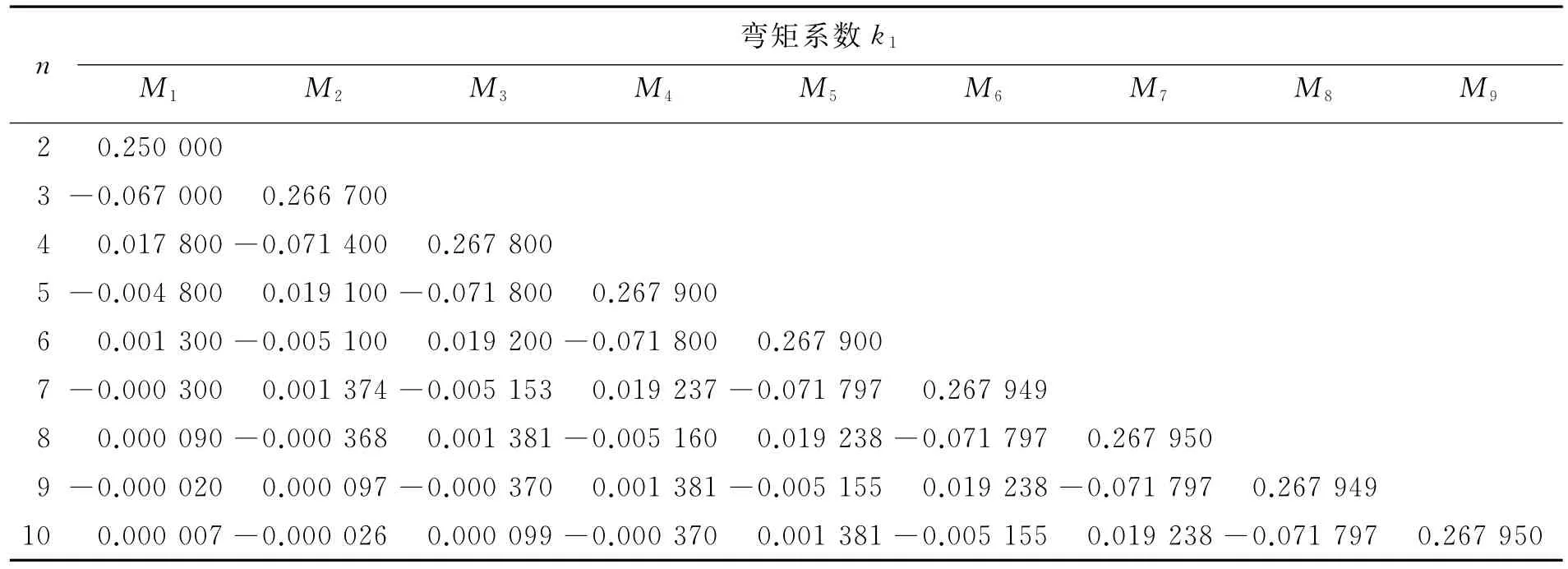
表1 等跨等截面连续梁在悬臂弯矩作用下支点弯矩系数k1

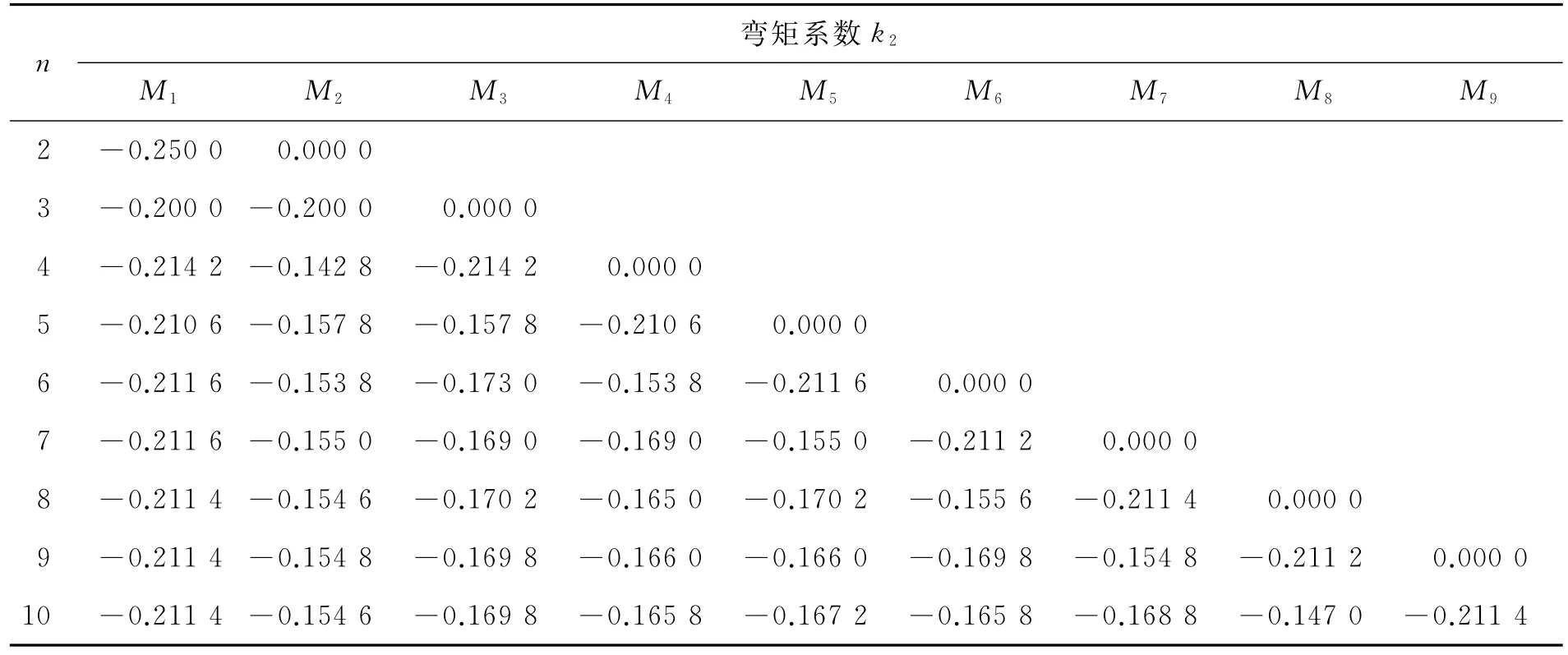
表2 等跨等截面连续梁在自重作用下支点弯矩系数k2

由表1、表2可以看出：随着跨数n的增加，悬臂端力矩和自重荷载集度对各支点造成的弯矩趋于稳定，当n≥3时悬臂端力矩Mn对连续梁中间支座造成的弯矩可忽略不计。

2.2 顶推第二阶段弯矩求解

根据对第一阶段弯矩值的分析，顶推悬臂端弯矩值对距离三跨之后的支点弯矩影响甚小。在顶推第二阶段，由于顶推跨后端支点n弯矩值受导梁刚度影响，建立解析平衡方程相对复杂。为此，将解析模型再次简化（见图2）。

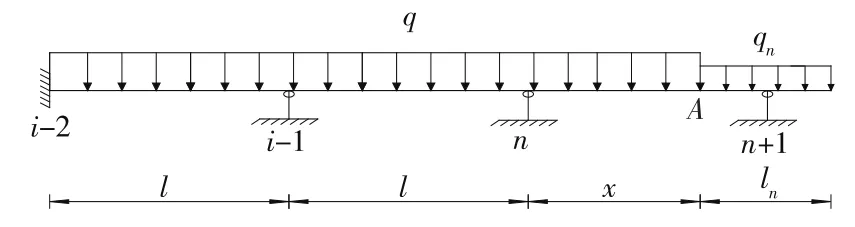
图2 顶推第二阶段简化后力学解析计算简图

根据位移法可建立各节点的平衡方程，支点n +1的平衡方程为：

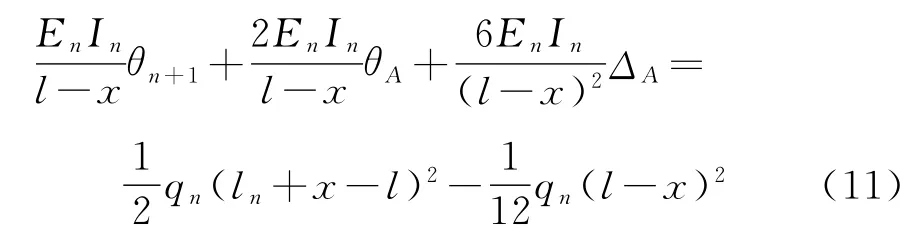
支点n的平衡方程为：

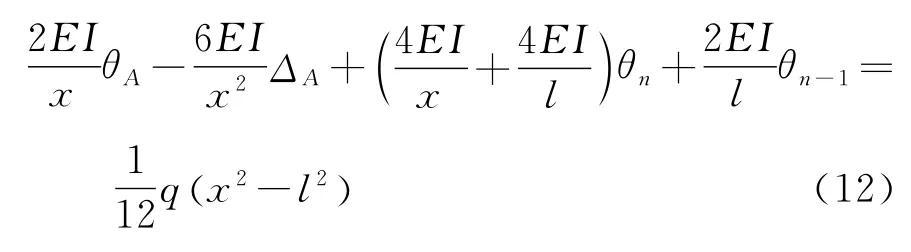
支点n-1的平衡方程为：

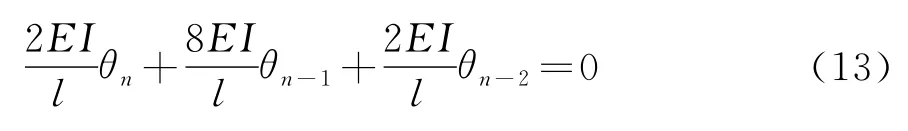
n-2点的平衡方程为：

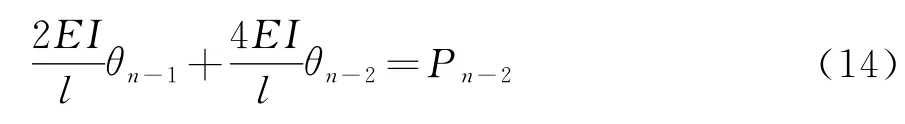
导梁、主梁连接点A的平衡方程为：

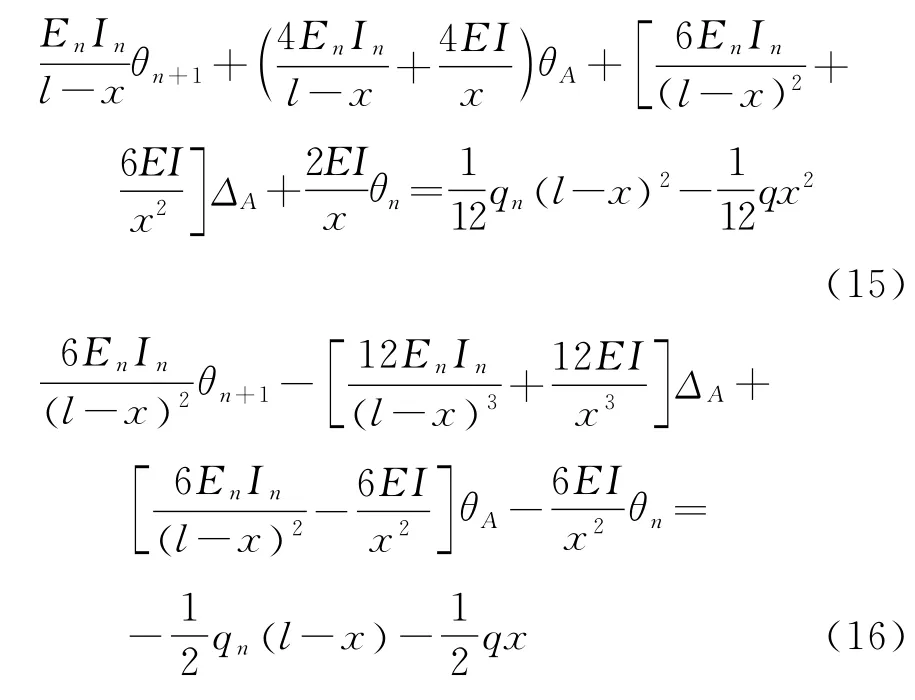
由假定的边界条件可知：

联立式（11）～（17），得顶推第二阶段支点n的弯矩为：

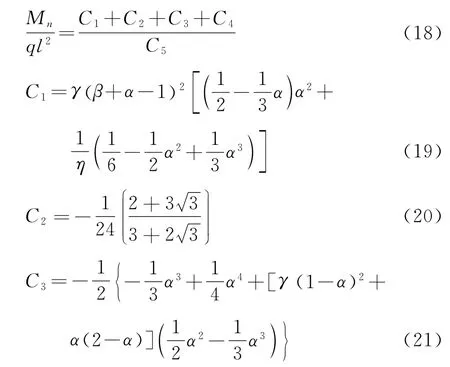
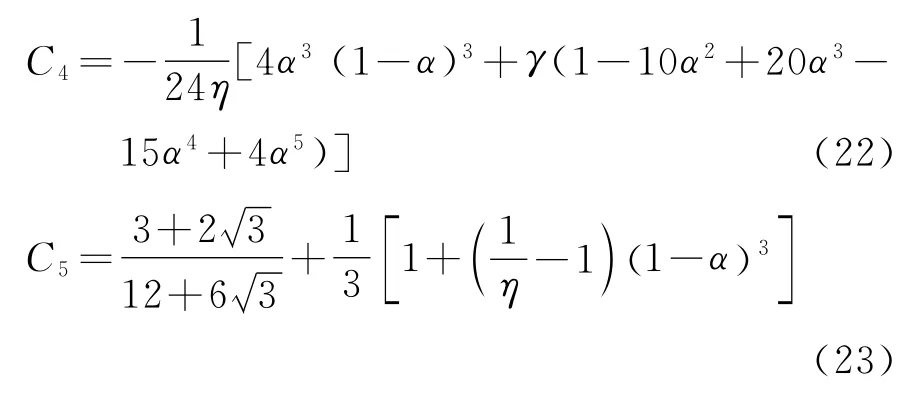
2.3 顶推第三阶段弯矩求解

根据上述假设，顶推第三阶段与顶推第一阶段相似，只是其计算跨数由n变成了n+1。顶推跨后端支点n的弯矩计算方法可理解为：在n+1跨，等跨等截面连续梁在顶推第一阶段中当α=0时中间支点n的弯矩值。根据前述分析，查表1、表2，得：

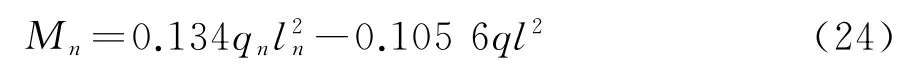
3 顶推导梁参数分析

3.1 导梁和主梁长度比、自重荷载集度比分析

顶推施工中，主梁内力最合理的状态是顶推各阶段主梁弯矩最大值接近，这样既可保证结构安全，又能节省材料。由前面的分析可知，主梁顶推过程中的内力与导梁设计刚度、长度、自重荷载集度均有关系。但在顶推第一和第三阶段，由于导梁处于完全悬臂状态，其自身刚度对主梁弯矩在各支点上的分配不产生影响。因此，在选取导梁合理设计长度时，先以第一和第三阶段作为计算根据。假设第一阶段末尾和第三阶段n点弯矩值相等，可得：

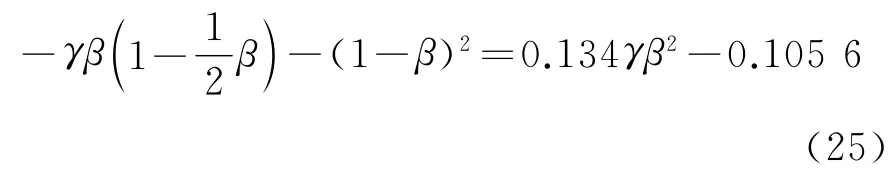
对式（25）进行简化，得：

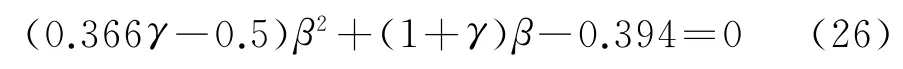
等跨等截面连续梁顶推施工中以主梁支点受力最优为原则时，导梁、主梁长度比β和自重荷载集度比γ之间的关系见图3。

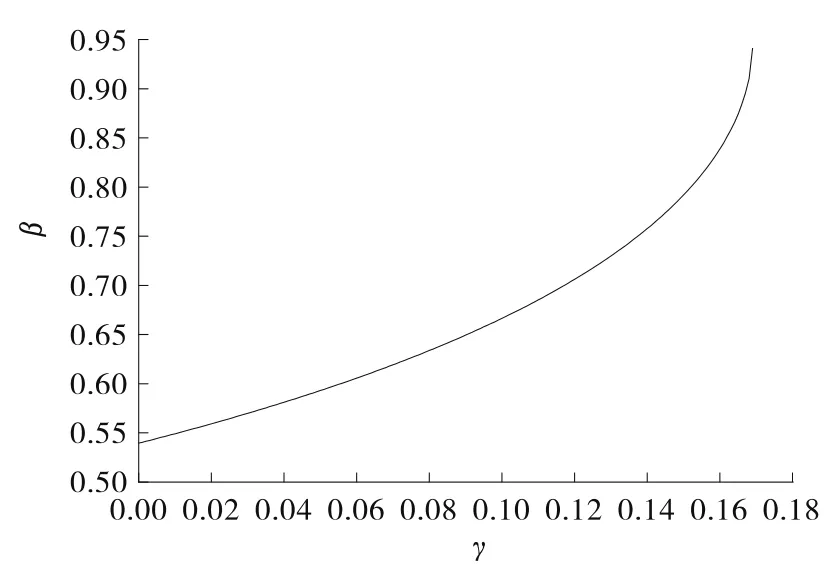
图3 满足Mn最优化时β与γ之间的关系曲线

由图3可以看出：在满足顶推跨后端支点弯矩Mn在顶推第一和第三阶段最优的情况下，导梁、主梁长度比β与自重荷载集度比γ正相关，γ值取得越大，相应的β值也应加大。但γ值不能超过0.169，否则式（26）将无解。这样就将顶推过程中导梁刚度、长度和自重荷载集度分析简化为了长度和自重荷载集度、刚度两个参数的分析。

3.2 导梁和主梁刚度比分析

由前文分析可知，导梁刚度大小会在顶推第二阶段对Mn产生影响，且该影响是非线性的。顶推设计和施工时应尽可能使顶推3个阶段的最大Mn值接近，以通过优化导梁设计而不是改变主梁结构的方式来控制Mn，这样更经济，也更节省时间。

在工程实践中，最为经济的导梁长度为顶推跨径的2／3，中国绝大多数PC梁桥采用的导梁长度多为顶推跨度的2／3～0.7。为更为直接地分析顶推过程中Mn值变化规律与η之间的关系，取β=0.66，此时最优的γ值应为0.096，支点n的弯矩值Mn随顶推进行的变化见图4。

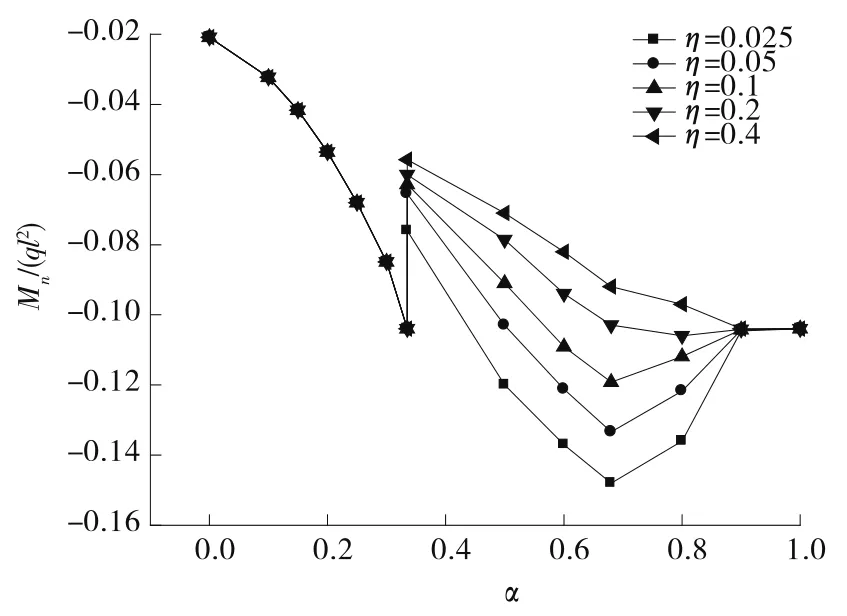
图4 β=0.66、γ=0.096时支点n的弯矩值Mn随顶推进行的变化

由图4可以看出：在导梁、主梁长度比β和自重荷载集度比γ处于最优关系时，导梁和主梁刚度比η＞0.2时，第二阶段Mn的最大值明显小于第一和第三阶段Mn最大值；当η＜0.2时，Mn最大值出现在第二阶段，且明显大于第一和第三阶段Mn最大值；当η=0.2时，顶推3个阶段的Mn最大值接近。可见，导梁和主梁刚度比取值稍小于0.2比较合适。若刚度减小，顶推过程中Mn最大值将增加，且愈加偏离顶推第一和第三阶段的Mn，将使梁体应力的控制成本加大；随着刚度的增加，顶推第二阶段Mn的最大值将愈加小于第一和第三阶段的Mn值，将使导梁成本增加，造成浪费。